寿险精算习题及答案讲解学习
寿险精算习题及答案讲解学习
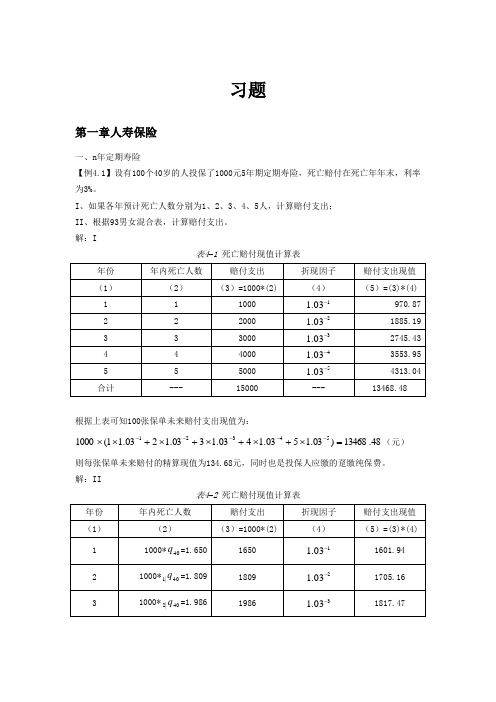
习题第一章人寿保险一、n 年定期寿险【例4.1】设有100个40岁的人投保了1000元5年期定期寿险,死亡赔付在死亡年年末,利率为3%。
I 、如果各年预计死亡人数分别为1、2、3、4、5人,计算赔付支出; II 、根据93男女混合表,计算赔付支出。
解:I表4–1 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:48.13468)03.1503.1403.1303.1203.11(100054321=⨯+⨯+⨯+⨯+⨯⨯-----(元)则每张保单未来赔付的精算现值为134.68元,同时也是投保人应缴的趸缴纯保费。
解:II表4–2 死亡赔付现值计算表根据上表可知100张保单未来赔付支出现值为:86.9124)03.103.103.103.103.1(1000540|4440|3340|2240|11402=⨯+⨯+⨯+⨯+⨯⨯-----q q q q q (元)则每张保单未来赔付的精算现值为91.25元,同时也是投保人应缴的趸缴纯保费。
【例4.2】某人在40岁时投保了10000元3年期定期寿险,死亡赔付在死亡年年末,利率为5%。
根据93男女混合表计算:I 、单位趸缴纯保费;II 、单位赔付现值期望的方差;III 、(总)趸缴纯保费; 解:I 、单位趸缴纯保费为,)()(424023414024040|2340|1240240|11|3:40q p v q p v vq q v q v vq q v Ak k k ++=++=⨯=∑=+]05.1001993.0)001812.01()00165.01(05.1001812.0)00165.01(05.100165.0[32⨯-⨯-+⨯-+=00492793.0=(元)。
II 、单位赔付现值期望的方差为,00444265.0)()()()(21|3:4040|2640|1440221|3:40240|)1(221|3:401|3:402=-++=-⨯=-∑=+A q v q v q v A q v AAk k k III 、趸缴纯保费为,28.49100001|3:40=⨯A (元) 【例4.3】某人在50岁时投保了100000元30年期定期寿险,利率为8%。
保险精算第二版习题及答案

保险精算第二版习题及答案保险精算(第二版)第一章:利息的基本概念练习题1.已知()2a t at b =+,如果在0时投资100元,能在时刻5积累到180元,试确定在时刻5投资300元,在时刻8的积累值。
(0)1(5)25 1.80.8,125300*100(5)300180300*100300*100(8)(64)508180180a b a a b a b a a a b ===+=?===?=+= 2.(1)假设A(t)=100+10t, 试确定135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.0833,0.0714(0)(2)(4)A A A A A A i i i A A A ---======—(2)假设()()100 1.1nA n =?,试确定 135,,i i i 。
135(1)(0)(3)(2)(5)(4)0.1,0.1,0.1(0)(2)(4)A A A A A A i i i A A A ---======3.已知投资500元,3年后得到120元的利息,试分别确定以相同的单利利率、复利利率投资800元在5年后的积累值。
11132153500(3)500(13)6200.08800(5)800(15)1120500(3)500(1)6200.0743363800(5)800(1)1144.97a i i a i a i i a i =+=?=∴=+==+=?=∴=+=4.已知某笔投资在3年后的积累值为1000元,第1年的利率为110%i =,第2年的利率为28%i =,第3年的利率为 36%i =,求该笔投资的原始金额。
123(3)1000(0)(1)(1)(1)(0)794.1A A i i i A ==+++?=5.确定10000元在第3年年末的积累值:(1)名义利率为每季度计息一次的年名义利率6%。
¥(2)名义贴现率为每4年计息一次的年名义贴现率6%。
保险精算课程三(寿险精算)
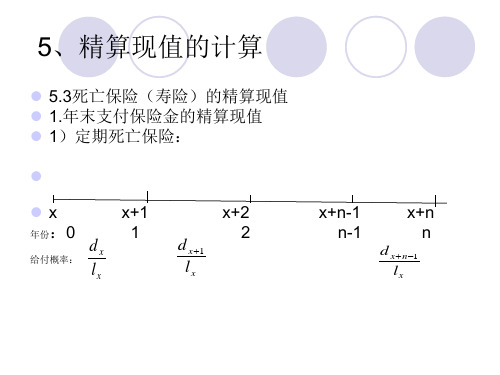
x
xn
x
xh
2.终身寿险的年缴纯保费
h Px
Ax ax:h|
Mx Nx Nxh
3.两全保险的年缴纯保费
P h x:n|
Ax:n| ax:h |
Mx
M xn Dxn Nx Nxh
课堂练习:
1.某人30岁投保20年期,延期10年,5年限期缴费的定期 人寿险,保险金额为100000元,求年缴纯保险费?
N x N x1 Dx
S x N x N x1
(Ia) x
Sx Dx
( Ia) x
S x 1 Dx
( Ia) x:n |
S x 1
S x n1 Dx
nN x n1
作业:
1.某人30岁(女)时投保寿险,约定45岁前死亡给付保险金 150000元,40岁至60岁之间死亡给付保险金为100000 元,60岁以后给付保险金50000元,求趸缴纯保险费?
(In| A)x (IA)1x:n| n|Ax
Rx Rxn nM xn N M xn
Dx
Dx
标准递减也可以看作:
A1 x:n |
A1 x:n 1|
A1 x:n 2|
A1 x:1|
nM x [Rx1 Rxn1 ] Dx
课堂练习
(x)=30,定期寿险保单。第一年死亡给付1000元, 第二年死亡给付1200元,第三年1400元,这样依次按 200元比例递增,n=20,求保险金的精算现值:
x:n |
Dx
Ax:n|
Mx
M xn Dx
Dxn
Ax
Mx Dx
m| Ax
M xm Dx
A1 x :n|
Mx
M Dx
寿险精算学(第3版)习题答案2

【解2.1】(1)可以被写成=(90−p(r200)18000,又由于达到极限寿命时=0,故=90。
(2)证明:因为,0=1;其次,达到极限寿命=90时,有90=0;且,的导数−110−218000<0,>0。
由此,生存函数的三个条件都被满足。
(3)93333.0)0()10(00010==S S p (4)(030−050)020(5)=−0'(p/0==110+218000−110−2因此,40=0.015833。
【解2.2】作为生存函数的基本属性有:(0)1,S =函数是单调递减的,同时lim ()0x S x →∞=。
(1)由于()exp[0.7(21)](10.72ln 2)xxS x x '=---⨯⨯,(0)0.51480S '=>,说明该函数不满足单调递减的性质。
所以,它不能作为生存函数。
(2)由于(0)1S =,3()2(1)0S x x -'=-+<,21lim ()lim0(1)x x S x x →∞→∞==+。
该函数可以作为生存函数。
(3)由于(0)1S =,()2()(2)0x S x ex -'=-<,lim ()0x S x →∞=。
该函数可以作为生存函数。
【解2.3】(1)4320751001)75(1)75(=--=-=S F (2)20017510040175)()75(=-==-=x x S dx d f (3)501412001)75()75()75(===S f μ【解2.4】(40)40(40)(40)40(40)(40)60(),060(40)60(40)1(),060(40)601()(),06060T t T T t T S t tS t p t S S t t t S t tf x p t t μμ+-===<≤'+=-=<≤+-==<≤【解2.5】()18)100(9)100(6)100(3100)100()100(2)]([2)]([3100)100()100()]([)100()100(222210002221000100022100022x x x x dt x t x t x T E dt p t x T Var xdt x t x dt p x T E x t x l l p xxx t xxx tx t x x t -=---=⎪⎭⎫⎝⎛------=-=-=---==---==⎰⎰⎰⎰----+【解2.6】所有表达式均为非负,因此需要验证是否满足0∞B =∞,使得0)(=∞S (1)∞==∞∞⎰0ln C BC dx BC xx,可以(2)∞=+=+∞∞-⎰001)ln()(x b a dx x b a ,可以(3)21)1(21)1(023=+-=+∞∞-⎰x dx x ,不可以【解2.7】把30.250x q +=代入120.170x q +=式中,得11232120.1700.680x x x x x x q p p q p p ++++++=⋅⋅=⇒=上式与已知条件11210.090x x x q p q+++=⋅=联立求解,解出10.770x p +=,20.117x q +=最后得1212(1)0.230.1170.347x x x x q q p q +++++=-+=+=【解2.8】由()1xS x ω=-,可知~(0,)X U ω,且有(20)~(0,20)T U ω-则[()]2x E T x ω-=,2()[()]12x Var T x ω-=已知020e 40=,即20401002ωω-=⇒=所以2(20)Var[T(20)]533.312ω-==【解2.9】首先计算K 的生存函数k012197k p +1015415则210414()09715151502210422()(21)13509715151513422()()[()]225E K p k k E K k p k k Var K E K E K ==++=∑==+⋅=⋅+⋅+⋅=∑==-=【解2.10】证明:(1)x t x x x t q t T t T p -=<-=≥=1)Pr(1)Pr((2)xu t x t x x x x ut p p u t T t T u t T t q +-=+≥-≥=+≤≤=)Pr()Pr()Pr((3)()()()tx u x t t x x x ut p p u T t T p ++⋅=≥⋂≥=Pr 【解2.11】(1)证明:110111111111+∞+∞+-∞∞+=+≤⋅+=+==⎰⎰⎰⎰⎰⎰x x x t x x t x t x t x t x e dt p dtp p dt p dt p dt p dt p e (2)证明:由于是关于的递减函数,因此有K1B≥所以xk x k k k kx tx t x e p dtp dt p e =≥==∑∑⎰⎰∞=+∞=+∞101【解2.12】证明:()()()()()()()t x t x x t S x t f x t S x t x t p p t t S x S x S x μμ+∂∂++-++====∂∂【解2.13】318.02005exp 20025exp 20015exp )5()25()15(200exp 100exp )(2225101020=⎪⎪⎭⎫⎝⎛-⎪⎪⎭⎫⎝⎛--⎪⎪⎭⎫ ⎝⎛-=-=⎪⎪⎭⎫⎝⎛-=⎭⎬⎫⎩⎨⎧-=⎰S S S q x dt t x S x 【解2.14】[][]8684284p =其中86l 已知,而[][][][][]2848484184841(1)(1)p p p q q ++==--由已知条件推导出[][][]85841848483144508030360.3225550803343640050800.20644556400q q q q q ++-=⋅=⋅=-==⋅⋅=⋅=【解2.15】(1)7[76]=83[76]=1192816608=0.718208(2)6|275+1=82−8475+1=0.084631【解2.16】40+1=40(1−40),40+2=402p [40],43=40+2−40∗2|40,46=43−40+1∗2|340+1.因此343=46/43=1−(1−40)2|340+1/(2p [40]−2|40)=1−(1−0.01608)×0.08964/(0.95977-0.02383)=0.905765【解2.17】151025:2525152540015100.040.04150.06015.40667t t tte p dt p p dtedt eedt--⨯-=+=+=⎰⎰⎰⎰【解2.18】(1)0.752.5=1−53.252.5=1−0.853+0.2540.552+0.553=0.0068381.7|1.252.5=54.2−55.452.5=0.854+0.255−0.655−0.4560.552+0.553=0.022690(2)0.752.5=1−0.5p 52.50.2p 53=1−520.5530.2=0.0068351.7|1.252.5=1.7p 52.51−1.2p 54.2=0.5p 52.5530.2p 541−0.8p 54.20.4p 55=520.553540.21−540.8550.4=0.022668【解2.19】因为{}10102102221exp ()=1exp 2()1exp ()1()1(1)2x x x x x q x t dt x t dt x t dt p q q q μμμ⎡⎤''=--+⎢⎥⎣⎦⎡⎤--+⎢⎥⎣⎦⎡⎤=--+⎢⎥⎣⎦=-=--=-⎰⎰⎰由此推出2x xq q '<。
寿险精算习题答案

寿险精算习题答案寿险精算习题答案寿险精算作为保险行业中的重要分支,是对寿险产品的风险和收益进行评估和计算的过程。
在寿险精算的学习过程中,习题是不可或缺的一部分,通过解答习题可以帮助我们更好地理解和掌握相关的知识。
下面,我们将一起来解答一些寿险精算的习题。
1. 问题:某寿险公司推出一款定期寿险产品,保险期限为20年,保额为50万,保费为每年1000元。
根据历史数据,该产品的死亡率为1‰。
请计算该产品的预期净保费。
解答:预期净保费是指在考虑风险的情况下,保险公司需要收取的保费。
根据题目给出的数据,我们可以得出以下计算公式:预期净保费 = 保费 - 风险保费风险保费 = 死亡率× 保额代入具体数值进行计算:风险保费= 0.001 × 500000 = 500预期净保费 = 1000 - 500 = 500所以,该产品的预期净保费为500元。
2. 问题:某寿险公司推出一款年金保险产品,保险期限为30年,保险年金为每年2万元,保费为每年5000元。
根据历史数据,该产品的终身年龄为85岁,死亡率为0.5‰。
请计算该产品的预期净保费。
解答:与上一题类似,我们还是需要计算风险保费。
不同之处在于,这是一款年金保险产品,保险期限为30年,但是保险金可能会在30年后一直支付到被保险人去世。
所以,在计算风险保费时,需要考虑被保险人在30年后的存活概率。
风险保费 = 死亡率× 保额× 存活概率存活概率 = 1 - 死亡率× 保险期限代入具体数值进行计算:存活概率 = 1 - 0.0005 × 30 = 0.985风险保费= 0.0005 × 20000 × 0.985 = 9.85预期净保费 = 5000 - 9.85 = 4990.15所以,该产品的预期净保费为4990.15元。
3. 问题:某寿险公司推出一款重大疾病保险产品,保险期限为10年,保额为50万元,保费为每年1000元。
中国精算师寿险与精算习题解答(1)

中国精算师寿险与精算习题解答(1)
1.风险的含义包括哪两个基本方面?请举例说明。
答:风险与三个因素直接有关:自然状态的不确定性、人的主观行为及两者结合所蕴涵的潜在后果。
形象地说,从潘多拉魔盒中飞出去的各种天灾人祸与被留在魔盒中的不可预知或不确定性结合在一起便构成了形成风险的两个方面。
例如,股票的涨跌与炒股者的买卖或不买或不买不卖行为便构成了形成风险的两个方面。
2.何谓风险态度?如何能够定量地刻画风险态度?
答:从某个决策问题出发,讨论一个决策者面对某种风险的反应或态度,常称之为风险态度,或者说是比较一群人各自的风险态度之间的差异程度。
假如有n个决策者DM1,DM2,…,DMn为了达到某个决策目标O而提出一系列备选方案.f,g,…,h,要在其中选择一个最优或最满意的方案,在这个问题框架下,可以研究相对于某项或某些方案的潜在后果来考察某个决策者的风险态度或者比较决策者之间风险态度的差别。
寿险精算作业及答案分解

作业1-1,假定i12分别为12%和6%, 请问在这两种不同的利率场合复利计 息,本金翻倍分别需要多少年?(请 分别用精确法和72法则求解,比较 求解结果)
• 精确法 when i(12) 12%
(11%)12n 2 n ln 2 5.8 12 ln1.01
when i(12) 6%
t m qx q tm x t qx t px tm px t px q m xt
k q0 k p0 1q0k q k 1 0 k q0 k p0 k 1 p0
k
0,
0
q0
1 4
q0
1 q0
1 4
,
p0
1
p0
1
q0
3 4,0p01113
k 1, 1 q0 4 4 1 p0 1q01 4 1q1
• 每年年末支付的利息为:
I Li 100005% 500
• 偿债基金的半年实际利率为:
j (1 j(4) )2 1 1.0152 1 3.02% 4
• 借款人每半年末存入偿债基金的款额为:
D 10000 1545.1 s
6 3.02%
等额偿债基金表
KI D
R
Jk
Ak
NBk
0 -- --
k 0
a 0:4
1 v 1 p0
v2 2 p0 v3 3 p0
3 32 321
1 4 1.06
43 1.062
432 1.063
2.3625
P1 A1 a
x:n
x:n x:n
P1 0.8663 0.3667 0:4 2.3625
趸缴情况:
k
0,
V1
0 0:4
寿险精算学(第3版)习题答案3

【解3.1】因为()()ln ()Pr Pr Pr T z F z Z z e z T δδ-⎛⎫=≤=≤=≥ ⎪-⎝⎭且由条件知剩余寿命服从De Moivre 分布,即()0,70T U ,故70ln ln 1ln ()Pr 17070z z z F z T dt δδδ-⎛⎫=≥==+ ⎪-⎝⎭⎰密度函数等于分布函数求导()ln 117070Z z f z zδδ'⎛⎫=+= ⎪⎝⎭已知0.05δ=,0.6z =代入上式得()0.60.48Z f =【解3.2】(40)的剩余寿命T 服从均匀分布(0,70),其生存函数为407070t tP -=,070t ≤≤由题意,可得ln 70ln ln ()Pr()Pr()Pr()ln 70t z z v F z Z z v z t v-=≤=≤=≥=Z 的90%置信上限即为使()0.9F z =的z 值,即ln 70ln 0.970zv -=解得exp[(70700.9)ln ]0.84z v =-⨯=【解3.3】在恒定死亡力和恒定利息力场合,容易验证趸缴净保费等于x A μδμ=+在调整以前有0.60.05μμ=+则求得0.075μ=调整以后0.0750.020.095μ'=+=,0.04δ'=则调整后的趸缴净保费为0.0950.7040.0950.04x A μμδ'===''++【解3.4】(1)()()tx A E Z E v ==,则()()2200.055001 1.250.031252500.0312522Pr[0]t x T x tt t A e f t dtedte dte Y δ∞-∞--+⎛⎫∞- ⎪⎝⎭====≥⎰⎰⎰其中~( 1.25,25)Y N -,则()1.25Pr(0)Pr(0.25)10.255Y Y +≥=≥=-Φ()0.031252[10.25]0.83x A e =-Φ=(2)因为22()x x Var Z A A =-,其中()()()2220.100.15001 2.50.1252500.12522[10.5]0.70t x T x tt t A e f t dte dte dte ∞-∞--+⎛⎫∞- ⎪⎝⎭====-Φ=⎰⎰⎰所以222()0.700.830.014x x Var Z A A =-=-=【解3.5】给付函数和贴现函数都已知,容易得到现时值函数为1(10.2)t t Z b v t -==+密度函数已知()()40400.02,050T t f t p t t μ=+=≤≤则趸缴净保费等于()()505000ln 10.21110.020.2410.2500.210t E Z dt t +⎛⎫=⨯=== ⎪+⎝⎭⎰两倍利息力下,趸缴净保费等于()()50502200110.020.020.091(10.2)0.210.2E Z dt t t -=⨯=⨯=++⎰所以现值变量的方差等于222()()[()]0.09090.23980.0334Var Z E Z E Z =-=-=【解3.6】一般情况下,如果剩余寿命T 服从()0,ω的均匀分布,即1(),0T f t t ωω=≤≤可以得到()0111t x T tt A e f t dte dtev a δωδωδωωωωδωδω∞---==-=-==⎰⎰本题中,T 服从(0,60)的均匀分布,故所求的净保费为604040100010001000666.76060a A =⨯=⨯=【解3.7】令3z 为()x 岁的人投保期末赔付1的n 年定期生存保险的现时值变量,根据已知条件有3()0.20.450.09n n x E z v p =⋅=⨯=223()0.040.450.018n n x E z v p =⋅=⨯=根据定期两全保险与定期寿险和定期生存险的关系,有213z z z =+则213123()()()()()()0.350.090.26E z E z E z E z E z E z =+⇒=-=-=[][]222213222212322()()()()()()()()0.060.0180.350.1645Var z E z E z E z E z Var z E z E z =+-⇒=-+=-+=推导出()[]2221110.16450.260.0969Var Z E Z E Z ⎡⎤=-=-=⎣⎦【解3.8】因为死亡服从De Moivre 分布,故40岁的人剩余寿命的密度函数为()160T f t =,060t ≤≤由于延期20年,所以赔付现值变量为0,020,2060TT Z e T δ-≤≤⎧=⎨<≤⎩所以,0z =点为重概率点,该点概率值为20201Pr(0)Pr(020)()603T Z T f t dt ==≤≤===⎰【解3.9】该保单可以视为一个10000元的终身寿险和10000元的20年定期寿险的组合,则该保单趸缴净保费为14545:201000010000A A +已知450.25A =,下面求145:20A 的值。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
lx1000(1),计算趸缴纯保费。
100000 1 1
20468.70 (元)
55
二、终身寿险
【例 4.4 】某人在 40岁时投保了 10000元终身寿险,死亡赔付在死亡年年末,利率为5%。根据
93男女混合表计算:
I、单位趸缴纯保费;II、单位赔付现值期望的方差;III、(总)趸缴纯保费;
死亡年度末给付,年利率 6%,参照生命表(U,93,1000000):
I、终身寿险;II、20年定期寿险;III、20年定期两全保险;IV、延期 10年终身寿险;V、延期 10年的20年定期寿险;VI、延期10年的 20年定期两全保险。
解、I、终身寿险:
A50M50D5011729.04 51090.53 0.229574
【例 4.6 】某人在 40岁时投保了10000元20年两全寿险,死亡赔付在死亡年年末,利率为5%。
根据 93男女混合表计算:
I、单位趸缴纯保费;II、单位赔付现值期望的方差;III、(总)趸缴纯保费;
解:I、单位趸缴纯保费为,A40:20|A410:20|A40:201|0.391722(元)
II
0.04x
,( x 0)。求赔付现值zt趸缴净保费、方差和
中位数
0.05。
解,fx(t)
S( x t)
S(x)
0.04(x
0.04e0.04(x
t)
0.04x
0.04t
0.04e0.04t,
趸缴净保费:
10|Ax
x
e
10
0.06t0.04
0.04t
e dt
0.04
xe0.1tdt
0.4e0.1t|10x0.4e10.147152
2A40
(A40)2
0.06593 ;
例 4.10】(x)投保终身寿险,
死亡即刻赔付 1元。假设余命服从常数死亡率分布,
利息力0.03。计算,I、Ax、D Ax;II 、Pr(zt0.9) 0.9 ,求0.9;III、假设有100 个(x)独立同分布的个体购买了该保险, 每人世纪缴纳保费为(1 R)Ax。在正态分布条件下 要使保费有 95%的概率足够支付死亡赔偿,计算R。
元的给付,利率 6%,根据93U生命表计算精算现值。
元) 3、延期终身生存年金
【例5.3 】对于( 30)从60岁起每年年初 6000元的终身生存年金,利率为 6%,试用93U生命表
求趸缴净保费。
4、延期定期生存年金
【例 5.4 】某人在 30岁时投保养老金保险,保险契约规定,如果被保险人存活到60岁,则确
2 1 2 3 4 5
1000
元) 则每张保单未来赔付的精算现值为 91.25 元,同时也是投保人应缴的趸缴纯保费。
【例4.2 】某人在 40岁时投保了 10000元3年期定期寿险, 死亡赔付在死亡年年末, 利率为5%。 根据 93男女混合表计算:
I、单位趸缴纯保费;II、单位赔付现值期望的方差;III
10
P
也就是说有 32.968%的死亡事件发生在延期范围内。 由于 0.32968<0.5 ,说明中位数不在重点 概率上。则,
r
0.04e
10
中位数 =17.33 。
第五章 生存年金
第一节 离散型年金
1、终身生存年金
【例5.1 】某人今年 45岁,花费 10000元购买了一份期末付终身生存年金产品,利率5%,根据
22
10|DA50:20|(DM60DM80DD80) /DD50(M60M80D80) /D50
2
(130.1094-18.522 40.7625)/2773.6211- ((9301.66- 2802.27 4312.51)/51090.53)20.010144
第三节 连续型(死亡即刻赔付)寿险趸缴纯保费
DA50DM50/ DD50M520/D520225.6235/2 773.6211-(11729.04 51090.53)20.028642II、 20年定期寿险:
A
DA510:20|(DM50DM70) / DD50(M50M70)2/ D520
2
(225.6235-60.4193)/2 773.6211-((11729.04-6149.05)/5 1090.53)20.047634
100 Var ( z)
二、延期定额寿险
0.9) Pr(t
fx(t)tpx x
0.9
tdt
z100
R)E( z)}
N(0,1)
1.96
10 R
DAx
ln
lnv
0.9)
t|
dt
2Ax
Pr(t
e(
)t
(Ax)2
t,则,
ln
ln
ln0 .9e
1
18
0.9)
0.9,
0.92 ln0.9
e
0.9,
N{ 100E (z),100Var ( z)},根据题意,
定给付 10年年金, 如果被保险人到 70岁依然存活, 则从70岁起获得生存年金。 如果年金每年 年初支付一次,每次支付 6000元,利率 6%,根据93U生命表计算趸缴净保费。
xt
解、在常数死亡力下,
tpxexp(
ds)
ut
,则,
I、
Ax
2Ax
II、Pr(zt
0.9)
tpx x tdt
(2 ) tdt
Pr(vt
t(余命)的密度函数
Pr(t
ln0.9)
ln
解得,
0.9
0.9;
III、zagg
z1
z2
Pr{zagg
100
(1
zagg100
E(z)
100 Var (z)
100 R E( z)
10|DA50:20|(DM60DM80) / DD50(M60M80) / D50
2
(130.1094-18.522)/2773.6211-((9301.66-2802.27)/5 1090.53)20.024048
VI、延期10年的 20年定期两全保险:
10|A50:20|(M60M80D80) / D50(9301.66- 2802.27 4312.51)/51090.53 0.211622
III
六、延期寿险
【例4.7 】某人在 40岁时投保了一份寿险保单, 死亡年年末赔付,如果在 40-60岁死亡,赔付
50000元;65-75岁死亡,赔付100000元;在75岁后死亡, 保险金为 30000元。利用生命表93U、利率 6%条件下的转换基数表计算该保单趸缴净保费。
解、这份保单可以分解为一份 50000元的25年定期寿险、一份 100000元延期 25年的 10年定期 寿险和一份 30000元延期35年的终身寿险的组合,即,
保费;II、单位赔付现值期望的方差;III、(总)趸缴纯保费;
解:I、单位趸缴纯保费为,A40:201|v2020p400.342332(元)
II、单位赔付现值期望的方差为,v2 2020p40 20q400.0313891
III
纯保费 +风险附加费用
四、n年定期两全保险
赔付支出
折现因子
赔付支出现值
(1)
(2)
(3)=1000*(2)
(4)
(5)=(3)*(4)
1
1
1000
1.031
970.87
2
2
2000
1.032
1885.19
3
3
3000
1.033
2745.43
4
4
4000
1.034
3553.95
5
5
5000
1.035
4313.04
合计
---
15000
---
13468.48
50000(13451.43 7800.72)700004432.388008.487(元)
93942.958008.487(元)
这份保单还可以分解为一份 30000元终身寿险、一份 200000元的 35年定期寿险和一份50000元延期 25年的 10年定期寿险的组合,即,
七、变额寿险
【例 4.8 】利用计算基数表求下列保单在被保险人50岁签单时的 1单位元趸缴纯保费和方差,
解:I、单位趸缴纯保费为,
64
k 1 2 3 65
A40vk|q40vq40v1|q40v2|q40... v64|q400.18853(元)。
k0
II、单位赔付现值期望的方差为,
64
2
k0
III、趸缴纯保费为,10000 A401885.29 (元)
三、n年定期生存寿险
【例4.5 】某人在 40岁时投保了 10000元20年定期生存寿险, 死亡赔付在死亡年年末, 利率为
93U生命表计算单位元精算现值的期望和方差,并计算每年可领取的金额。
解、a45
N46
1610605 .74615.128
D45
106465.32
Da45
1
2
2
[DM45(M45)2](1 i)2
[DM45
(M45)2]
d2
[DD45(D45) ]i2
DD45
D45
2
1.05
2
0.05
每年可领取金额
【例 5.2 】某人在 40岁购买了一份 20年定期生存年金产品,如果存活可在每年年初领取1000
Pr{
AxDAx
zagg100 E( z)
