人教版三年级上册数学奥数数阵图进阶课件
数阵图-奥数优秀课件

【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三 数之和都等于13。
【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三数之和都 等于13。
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
2+3+4+5+6=20 中间的数是 : 26-20=6 2+5=4+3=7
【经典例题】
例题1 把2~6这五个数分别填入下图的“○”中,使得横行三数之和与竖列三数之和都 等于13。
解析: 横行三数之和与竖列三数的和是 : 13×2=26 各个数的和是:
7个数字总和:(1+7)×7÷2=28
中间数字为:30-28=2
2÷2=1
边上的数字和:10-1=9,
2+7=4+5=3+6
(答案不唯一)
【课堂练习】
练习3: 把3~9这七个数字分别填入下图的各“○”中,使每条线上三个“○”内数的和等
于16.
【课堂练习】
练习3: 把3~9这七个数字分别填入下图的各“○”中,使每条线上三个“○”内数的和等
【思路导航】 设中间两个圆中的数为a、b,则两个大圆的总和是1+2+3 +……+10+a+b=30×2,即55+a+b=60,a+b=5。在 1——10这十个数中1+4=5,2+3=5。 当a和b是1和4时,每个大圆上另外四个数分别是(2,6,8, 9)和(3,5,7,10);当a和b是2和3时,每个大圆上另 外四个数分别为(1,5,9,10)和(4,6,7,8)。
2020人教北师大版奥数教材提高二年级三年级数学数阵图解题技巧综合上课PPT教学课件

6
2
、
5
7
找数字最多的线 例3:在正方形中填上合适的数,使横行、竖行、斜行上 的三个数相加都等于18.
、
找数字最多的线 练1:在下图中填上合适的数,使横行、竖行、斜行三个 数的和都等于27。
、
找数字最多的线 练2:在下图中填上合适的数,使横行、竖行、斜行三个 数的和都等于21。
、
勇闯迷魂阵
类型②:填和、 未知的数阵
、
数排序,头中尾填中间 练2:将1、2、3、4、5、6、7填入下图中,使每条线上 的三个数的和都等于10。
、
通关技巧
数阵图的秘密(笔记)
1.和已知,找数字出现最多的线,用加减法去算;
2.和未知,先确定中间值
技巧:数排序,头中尾任选、一个填中间,大小大小手拉手;
3.九宫格:中间数×3=和
数排序,头中尾填中间 挑战:把1~9这九个数填入下图中,使横行、竖行、斜 行三个数的和都相等。
数阵图的秘密
**老师
勇闯迷魂阵:
认识数、 阵图
数阵图
数阵图的秘密(笔记)
特点:每条线每条边上的数相加的和都相等
2 、
1
5
4
3
数阵图类型 1.发射型:
数阵图的秘密(笔记)
、
数阵图类型 1.封闭型:
数阵图的秘密(笔记)
、
数阵图
数阵图的秘密(笔记)
要求:在空格里填数,每条线每条边上的数相加和都相等
、
数排序,头中尾填中间 练2:把2、3、4、5、6、7、8这七个数填入下面的圆中, 使每条线上的三个数和都相等.
、
数排序,头中尾填中间 例2:把1、2、3、4、5这五个数填入图中的方格中,使 横行、竖行三个数的和都相等10.
学而思三年级奥数第9讲.数阵图进阶
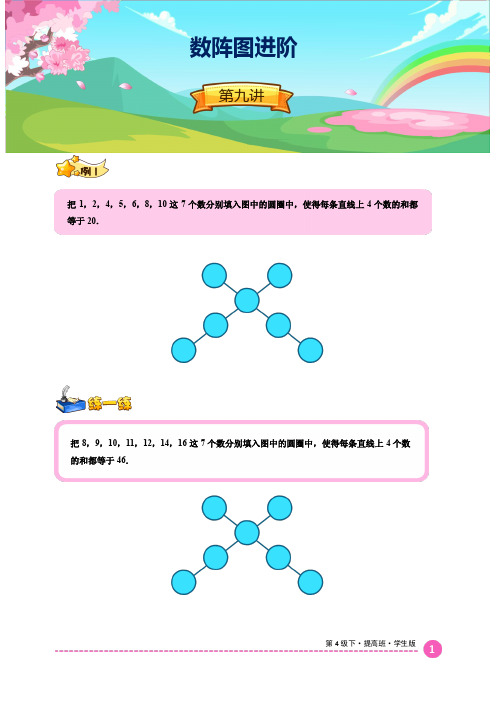
把8,9,10,11,12,14,16这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于46.把1,2,4,5,6,8,10这7个数分别填入图中的圆圈中,使得每条直线上4个数的和都等于20.数阵图进阶第九讲第4级下·提高班·学生版第4级下·提高班·学生版把2,3,4,5,6,7,8这七个数分别填入图中的圆圈中,使两个正方形中四个数之和都等于19. 将5,9,13,14,17,21,25这7个数分别填入图中的圆圈中,使得每条直线上3个数的和都等于44.第4级下·提高班·学生版将5,6,9,11,14,15这6个数分别填入图中的圆圈里,使两个大圆上4个数的和都等于40.把1,5,9,10,16,21这6个数分别填入图中的○里,使每一个大圆上的四个数之和都等于36.第4级下·提高班·学生版1. 把5,6,7,8,9这5个数分别填在下图的内,使横行、竖列3个数的和都等于( )中的数.把1,3,4,5,6,8,11,15这8个数分别填入图中的圆圈里,使得每个大圆上5个数的和都等于33.第4级下·提高班·学生版2. 把3,5,7,9,11,13,15这7个数分别填入图中的圆圈内,使每条直线上的3个数的和都等于27.3. 把2,4,6,8,10,12,14,16,18这9个数分别填入下图的圆圈中,使得每条直线上的3个数的和都等于24.4.把2,3,4,5,6,7,8这七个数分别填入图中的圆圈内,使两个正方形中四个数之和都等于21.5.把1,2,4,5,6,11这6个数分别填入图中的○里,使每个圆圈上的四个数之和都等于22.第4级下·提高班·学生版第4级下·提高班·学生版6. 把2,5,6,8,10,12,14,22这8个数分别填入下图中,使得每个大圆上的5个数的和都等于49.思维跳板——剪指甲小华的爸爸1分钟可以剪好5个自己的指甲.那么,他在5分钟内可以剪好几个自己的指甲呢?。
三年级3数教程 数阵图2
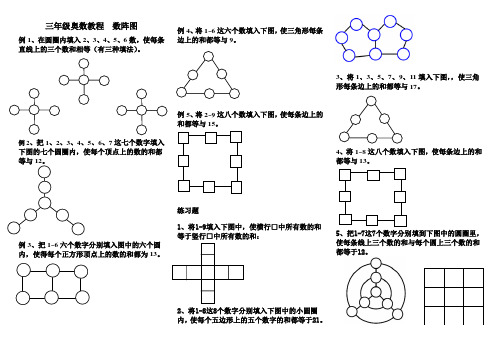
三年级奥数教程 数阵图
例1、在圆圈内填入2、3、4、5、6数,使每条直线上的三个数和相等(有三种填法)。
例2
、把1、2、3、4、5、6、7这七个数字填入下图的七个圆圈内,使每个顶点上的数的和都
等与12。
例3、把
1~6六个数字分别填入图中的六个圆内,使得每个正方形顶点上的数的和都为13。
例4、将
1~6这六个数填入下图,使三角形每条边上的和都等与9。
例5、将2~9这八个数填入下图,使每条边上的和都等与15。
练习题
1、将1-9填入下图中,使横行□中所有数的和等于竖行□中所有数的和:
2、将1-8这8个数字分别填入下图中的小圆圈内,使每个五边形上的五个数字的和都等于21。
3、将1、3、5、7、9、11填入下图,,使三角形每条边上的和都等与17。
4、将1~8这八个数填入下图,使每条边上的和都等与13。
5、把1-7这7个数字分别填到下图中的圆圈里,使每条线上三个数的和与每个圆上三个数的和都等于12。
三年级奥数1-数阵图

课题数阵图教授教养目的1:懂得两种类型数阵图概念;2:能按照题中具体请求填数阵图重点填图三步调:1.算出1个(或几个)重叠数的值(或和)2.经由过程重叠数的值(或和)找出重叠数3.把数阵图填写完全难点经由过程找到重叠数填数阵图专题1:数阵图在平庸的数学王国中,有一类异常有味的数学问题,它变更多端,惹人入胜,奥妙无限.它就是数阵,一座真正的数字迷宫,它对爱好探讨数字纪律的人有着极大的吸引力,以至有些人留连个中,用平生的精神来研讨它的变更,就连大数学家欧拉对它都有着浓重的兴致.那么,到底什么是数阵呢?我们先不雅察下面两个图:上面两个图就是数阵图.精确地说,数阵图是将一些数按照必定请求分列而成的某种图形,有时简称数阵.一.辐射型数阵图先从几个简略的例子开端.把1~5这五个数填入下页左上图中的○里(已填入5),使两条直线上的三个数之和相等.1.2 把1~5这五个数分离填在左下图中的方格中,使得横行三数之和与竖列三数之和都等于9.练一练:将1~9这九个数分离填入右上图中的○里(个中9已填好),使每条直线上的三个数之和都相等.还有其他填法吗?例2将1~7这七个天然数填入左下图的七个○内,使得每条边上的三个数之和都等于10.假如把例2中“每条边上的三个数之和都等于10”改为“每条边上的三个数之和都相等”,其他不变,那么模仿例1,重叠数可能等于几?如何填?练一练:将 10~20填入左下图的○内,使得每条边上的三个数字之和都相等.二、关闭性数阵例3将1~8这八个数分离填入右图的○中,使两个大圆上的五个数之和都等于21.练一练:把1~8填入下页左上图的八个○里,使每个圆圈上的五个数之和都等于20.例4 将1~6这六个天然数分离填入右图的六个○内,使得三角形每条边上的三个数之和都等于11.将2~9这八个数分离填入右图的○里,使每条边上的三个数之和都等于18.附加:把1~7分离填入左下图中的七个空块里,使每个圆圈里的四个数之和都等于13.你学会了吗1.将3~9这七个数分离填入下图的○里,使每条直线上的三个数之和等于20.2.将1~11这十一个数分离填入图的○里,使每条直线上的三个数之和相等,并且尽可能大.3.把5.6.7.8.9.10.11.12.12.14填入下图,使每个大圆圈中六个数的和是554.将1~8填入左下图的八个○中,使得每条边上的三个数之和都等于15.功课:1.将1~9这九个数分离填入右图的小方格里,使横行和竖列上五个数之和相等.(有若干种填法?)2.把1~6这六个数填入右上图的○里,使每个圆圈上的四个数之和都相等.3.将4.5.6.7.8.9六个数填鄙人图,使每条边上得三个数之和都相等,并且和为最大,和为最小呢?4.把1——7这7个数,分离填入途中,使直线和大圆上的数之和相等生涯趣题:小猫要把15条鱼分成数目不相等的4堆,问最多的一堆中最多可放几条鱼?。
三年级奥数教程第13讲 数阵图

三年级奥数教程第13讲数阵图例1、把1~6这六个数字分别填入图13一l的六个圈内,使得每个正方形顶点上的数的和都为13.分析从1到6这六个数的和是21.而两个正方形8个顶点上的数之和是26(=13×2),比六个数的总和大5.这是因为中间两个圈内的数,都被算了两次,所以,多出来的5就是中间两个圈内的数的和.解在1到6六个数中,两个数的和为5,只可能是1+4、2+3.当中间两个圈内填1与4时,剩下的四个数,3与5、2与6配对即可以满足条件.当中间两个圈内填2与3时,剩下的四个数无法组成和相等的两对,因而无法满足条件.所以,得到如图13—2的填法.随堂练习1将3、4、6这三个数填入图13—3的三个圆圈内,使得每条边上的三个数的和等于11.例2、将2到7这六个数,填入图13—4的圈中,使得每条线上的三个数的和相等.分析与解将三条线上的三个数都相加,中间的1被加了3次,所以三条线上三个数的和为1+2+…+6+7+1+1=30.从而每条线上的和是10(=30÷3),即每条线上剩余两个圆圈内数的和是9(=10—1).由 2+7=4+5=3+6=9.可以得到如图13—5的解.随堂练习2 将1到7这七个数填入图13—6,使得每条线上的三个数的和相等.例3、将1到9这九个数填入图13—7,使得从中心出发的每条线段上的三个数的和相等.分析与解先来确定中心的数.设这个数为a,则4条线上12个数(中心的数出现4次,其余的数各出现一次)的和1+2+…+9+a+a+a是4的倍数,即45+3×a是4的倍数.所以a只可能是1、5、9.(1)当a=1时,2与9、4与7、8与3、5与6两两搭配填入同一条线的两个圈内即可.(2)当a=5时,l与9、2与8、3与7、4与6搭配.(3)当a=9时,1与8、2与7、3与6、4与5搭配.这样得到如图13—8所示的三个解.随堂练习3 将1~8填入图13—9,使两个正方形顶点上的数的和相等,并且用斜线连接的4对数的和也都相等.例4、将1到5这五个数填入图13-10,使得圆周上四个数的和与每条直线上的三个数的和都相等.分析与解设处于中心圈内的数是a,因为竖线上的三个数的和等于圆周上的四个数的和,所以a等于它左、右两个数的和.同理,a等于它上、下两个数的和.从而a是最大的数5.其余四个数,2与3搭配,1与4搭配,写在同一条线上.得到的解如图13—11所示.随堂练习4 在图13一12中圆圈内填上7、8、10、12,使得每个圆内的四个数的和相等.例5、将1~6这六个数填入图13~13的六个圆圈内,使得每条边上的三个数的和相等.分析与解用字母a、b、c表示三个顶点上的数.如果l、6都在边上,那么a、b、c中有两个数的差是5(=6—1).这不可能.所以可设以a=1或6.如果a=1,那么由2+6=3+5.3+6=4+5.可得图13—14的(1),(2).如果a=6,同样可得图13—14的 (3),(4).随堂练习5 将l到16填入图13—15,使得每条线段上四个数的和相等,两个八边形八个顶点上的数的和也相等.例6、将1~16填入图13—16的正方形,使每行、每列、每条对角线的和都相等.图13—16分析与解本题也就是造一个四阶幻方.四阶幻方的造法很多,解也不惟一.下面介绍一种最简的做法,可以称为调整法.先将1~16依照次序先左后右,先上后下逐一填入图13—17(1)中得1234114154115144 567896712126799101112510118810115 13141516132316133216⑴⑵⑶图13—17四阶幻方中每行和、每列和、每条对角线的和都是 (1+2+…+16)÷4=(1+16)×16÷2÷4=34.现在图13—17(1)的两条对角线的和都已经是34,合乎要求.所以对角线上的数不要再动.先来调整行.将第一行的2、3分别与第四行的14、15对调,第二行的5、8分别与第三行的9、12对调,得图13—17(2),这个图中,不但每条对角线的和是34,每一行的和也都是34.再调整列.将图13—17(2)第一列的9、5分别与第四列的12、8对调,第二列的14、2分别与15、3对调,得图13—17(3),这个图就是一个合乎要求的幻方.随堂练习6 比较例6所得的幻方与随堂练习5的答案.有何联系?读一读……………………………………………………可能与必然上节末,说到一个游戏“数独”.数独怎么填呢?比如先看第一行,在上节末的图中,有6个空格,应填1、2、4、7、8、9这6个数字.每个空格填的数有6种可能,难以确定.如果看第二列,只有2个空格,应填2、7,每个空格有2种可能,但还不能惟一确定.可能性太多,需要逐个枚举讨论,比较麻烦.所以应先考虑可能较小的方格.最好能发现一些方格,只有一种填法,也就是说这些方格填什么数是必然的.将这些方格先填好,对填其他方格会有帮助.同时考虑几个方面的要求,可以得到必然的填法.比如中间的3×3的正方形,只有3个空格,应填2、6、8.再结合第四行已经有8,第六行也已经有8,所以8必须填在中央.接下去,因为第四行已经有6,所以6必须填在第六行,2填在第四行.现在再看第四行,只剩2个空格,应填9与3.第九列有9,所以第四行的9只能(必然)在第三列,3在第九列.同样,右中3×3的正方形中,9必然在第六行.第六行第一列必填2.左中3×3的正方形中,5必在第一列,7在第三列.第八列3必填在第九行,9必填在第二行.右上3×3的正方形中,7必填在第七列.右下3×3的正方形中,5必在第八行第七列,2必在第八行,1在第九列第七行,6在第七行第七列.右中3×3的正方形中,6在第九列,2在第七列.左下3×3的正方形中,2、3、8、6的填法都是必然的.左上3×3的正方形中,按行依次填2、1、4、7、6.右上3×3的正方形中,填4、8.中上3×3的正方形中填8、9、6、2、7、4.中下3×3的正方形中填9、3、6、4、1、7.填法都是必然的。
三年级奥数提高班-第5讲-数阵图
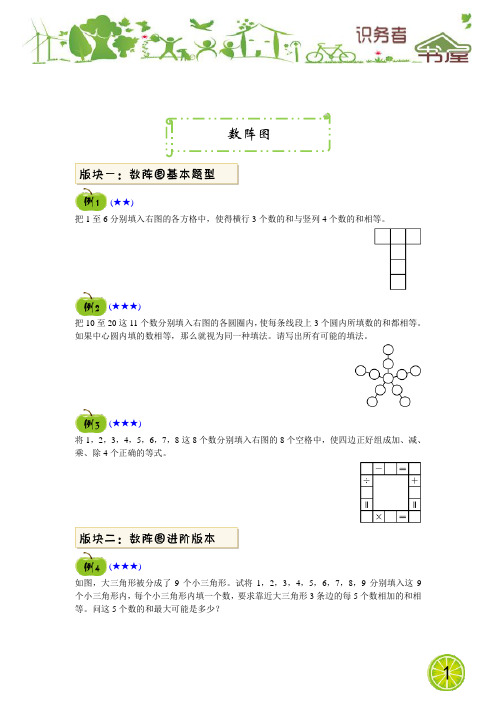
把1至6分别填入右图的各方格中,使得横行3个数的和与竖列4个数的和相等。
把10至20这11个数分别填入右图的各圆圈内,使每条线段上3个圆内所填数的和都相等。
如果中心圆内填的数相等,那么就视为同一种填法。
请写出所有可能的填法。
将1,2,3,4,5,6,7,8这8个数分别填入右图的8个空格中,使四边正好组成加、减、乘、除4个正确的等式。
如图,大三角形被分成了9个小三角形。
试将1,2,3,4,5,6,7,8,9分别填入这9个小三角形内,每个小三角形内填一个数,要求靠近大三角形3条边的每5个数相加的和相等。
问这5个数的和最大可能是多少?
数阵图
(★★)
(★★★)
(★★★)
(★★★)
(★★★★)
请在下图中的7个小圆圈内各填入一个自然数,使得图中给出的每个数都是相邻两个圆圈中所填数的差(大数减小数),并且所填的7个数之和是2011。
三年级奥数数阵图PPT课件

5 1 4 7
2
第15页/共18页
将1-6这六个数字填入下图的圆圈中,使每个大 圆圈上4个数字之和为14。
3
1
2
4
6
5
第16页/共18页
把2~7这六个数填入右上图的○里,使每个圆圈 上的四个数之和都等于18。
6
4
2
3
5
7
第17页/共18页
Thanks!
第18页/共18页
1
5
3
2
4
A
7
8
6
9
第6页/共18页
将1-9这九个数填入下图圆圈内,使横行、竖行五个数相加和 为25。
1
横行、竖行五数和:25+25=50 1-9数之和:1+2+3+4+5+6+7+8+9=45 50-45=5 12346789八个数分为两组,使每组中 四个数 字之和 : 25-5=20 则1+4+6+9=2+3+7+8
4
5
2
3
7
8
6
9
第7页/共18页
将1-9这九个数填入下图圆圈内,使每条线上三个 数字相加之和为12。
2
3
4
四条线数之和: 12×4=48 1-9数之和:1+2+3+4+5+6+7+8+9=45 A:(48-45)÷3=1 剩下的数字平均分成四组,每组数字 之和12- 1=11 所以应为: 2+9、3+8、4+7、5+6。
10-1=9 则2+7=3+6=4+5
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
目录
01
单击添加标题
02
单击添加标题
03
单击添加标题
04
单击添加标题
01 点击添加文字
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里,或者通过复制您的文本 后,在此框中选择粘贴,并选择只保留文字。 在此录入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。 您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。
以下赠品教育通用模板
前言
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。您的内容打在这 里,或者通过复制您的文本后,在此框中选择粘贴,并选择只保留文字。 在此录入上述图表的综合描述说明。 您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。您的内容打在这 里,或者通过复制您的文本后。
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入这里,或者 通过复制您的文本后,在 此框中选择粘贴,并选择 只保留文字。在此录入上 述图表的综合描述说明。
一、数阵图定义及分类:
定义:把一些数字按照一定的要求,排成各种 各样的图形,这类问题叫数阵图. 数阵:是一种由幻方演变而来的数字图. 数阵图的种类繁多,这里只向大家介绍三种数 阵图:即封闭型数阵图、辐射型数阵图和复合 型数阵图.
二、解题方法: 解决数阵类问题可以采取从局部到整体再 到局部的方法入手:
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。
01 点击此处添加标题 02 点击此处添加标题 03 点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里,或者 通过复制您的文本后,在 此框中选择粘贴,并选择 只保留文字。在此录入上 述图表的综合描述说明。
您的内容打在这里,或者 通过复制您的文本后,在 此框中选择粘贴,并选择 只保留文字。在此录入上 述图表的综合描述说明。
您的内容打在这里,或者 通过复制您的文本后,在 此框中选择粘贴,并选择 只保留文字。在此录入上 述图表的综合描述说明。
02 点击添加文字
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并选择只 保留文字。在此录入上述图表的综合描述说明。您的内容打在这里,或者通过 复制您的文本后,在此框中选择粘贴,并选择只保留文字。在此录入上述图表 的综合描述说明。您的内容打在这里,或者通过复制您的文本后,在此框中选 择粘贴,并选择只保留文字。在此录入上述图表的综合描述说明。
例1、把 1,2,4,5,6,8,10 这 7 个数分别填入图中的圆圈中,使得 每条直线上 4 个数的和都等于 20.
通关小诀窍:确定中间值
把 8,9,10,11,12,14,16 这 7 个数分 别填入图中的圆圈中,使得每条直线上 4 个数 的和都等于 46.
例2 、将 5,9,13,14,17,21,25 这 7 个数分别填入图中的圆圈中,使得每条直线 上 3 个数的和都等于 44.
把1~11填入图中,使每条线上三个数的和相等.
例3、把 2,3,4,5,6,7,8 这七 个数分别填入图中的圆圈中,使两个 正方形中四个数之和都等于 19.
例4、 把1——8八个数分别填入下图的○内,使 每个大圆上五个○内数的和是20。
将1——10这十个数填入下图小圆中,使每 个大圆上六个数的和是30。
第一步:区分数阵图中的普通点(或方格)和关键点(或方格); 第二步:在数阵图的少数关键点(一般是交叉点)上设置未知 数,计算这些关键点与相关点的数量关系, 得到关键点上 所填数的范围; 第三步:运用已经得到的信息进行尝试.这个步骤并不是对 所有数阵题都适用,很多数阵题更需要对 数学方法的综合 运用.
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里,或者通过复制您的文本后, 在此框中选择粘贴,并选择只保留文字。在此录 入上述图表的综合描述说明。
您的内容打在这里,或者通过复制您的文本后,在此框中选择粘贴,并 选择只保留文字。在此录入上述图表的综合描述说明。
例5、把 1,5,9,10,16,21 这 6 个 数分别填入图中的○里,使每一个大圆上的 四个数之和都等于 36.
将 5,6,9,11,14,15 这 6 个数分别 填入图中的圆圈里,使两个大圆上 4 个数 的和都等于40.
把 1,3,4,5,6,8,11,15 这 8 个数 分别填入图中的圆圈里,使得每个大圆上 5 个数的和都等于 33.
点击此处添加标题
您的内容打在这里,或者通过复制您的文本 后,在此框中选择粘贴,并选择只保留文字。 在此录入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里,或者通过复制您的文本 后,在此框中选择粘贴,并选择只保留文字。 在此录入上述图表的综合描述说明。
点击此处添加标题
您的内容打在这里,或者通过复制您的文本 后,在此框中选择粘贴,并选择只保留文字。 在此录入上述图表的综合描述说明。
