学而思三年级奥数第 讲 数阵图进阶
小学三年级奥数 第39讲：数阵图
【例4】(★★★★★) 将1~7七个数字填入下图的七个○内，使每个圆周和每条直线上的 三个数之和都相等。
【例5】(★★★★) 将1~6这六个数字分别填入下图的六个○内，使得三条直线上的数 字之和都相等。
【例6】(★★★★★) 如图所示，大三角形被分成了9个小三角形。试将1，2，3，4，5，6， 7，8，9分别填入这9个小三角形内，每个小三角形内填一个数，要 求靠近大三角形3条边的每5个数相加的和相等，问这5个数的和最大 可能是多少？
数阵图
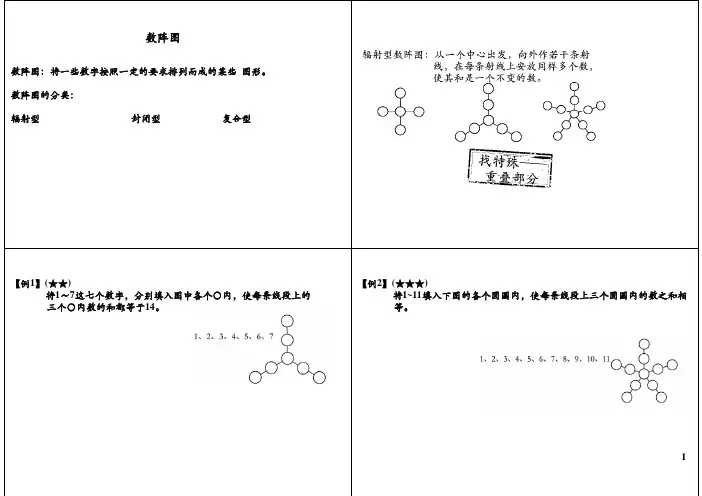
数阵图：将一些数字按照一定的要求排列而成的某些 图形。
数阵图的分类：
辐射型
பைடு நூலகம்封闭型
复合型
【例1】(★★) 将1～7这七个数字，分别填入图中各个○内，使每条线段上的 三个○内数的和都等于14。
【例2】(★★★) 将1~11填入下图的各个圆圈内，使每条线段上三个圆圈内的数之和相 等。
1
【例3】(★★★) 你能把1～6六个数字分别填入下图的六个圆圈中，使每一边三个数相 加的和都等于11吗？
2
【本讲总结】 数阵图 一、分类
辐射型
封闭型
复合型
二、基本关系 各数之和＋重叠数×重叠次数＝线和×线数
三、辐射型数阵图 窍门：掐头、去尾、取中间
四、注意事项 (a)关键点：特殊位置 (b)(b) 复合型:在调整的时候，不能改变原有边和
3
学而思三年级奥数第9讲.数阵图进阶
把8，9，10，11，12，14，16这7个数分别填入图中的圆圈中，使得每条直线上4个数的和都等于46．把1，2，4，5，6，8，10这7个数分别填入图中的圆圈中，使得每条直线上4个数的和都等于20．数阵图进阶第九讲第4级下·提高班·学生版第4级下·提高班·学生版把2，3，4，5，6，7，8这七个数分别填入图中的圆圈中，使两个正方形中四个数之和都等于19． 将5，9，13，14，17，21，25这7个数分别填入图中的圆圈中，使得每条直线上3个数的和都等于44．第4级下·提高班·学生版将5，6，9，11，14，15这6个数分别填入图中的圆圈里，使两个大圆上4个数的和都等于40．把1，5，9，10，16，21这6个数分别填入图中的○里，使每一个大圆上的四个数之和都等于36．第4级下·提高班·学生版1． 把5，6，7，8，9这5个数分别填在下图的内，使横行、竖列3个数的和都等于( )中的数．把1，3，4，5，6，8，11，15这8个数分别填入图中的圆圈里，使得每个大圆上5个数的和都等于33．第4级下·提高班·学生版2. 把3，5，7，9，11，13，15这7个数分别填入图中的圆圈内，使每条直线上的3个数的和都等于27．3. 把2，4，6，8，10，12，14，16，18这9个数分别填入下图的圆圈中，使得每条直线上的3个数的和都等于24．4.把2，3，4，5，6，7，8这七个数分别填入图中的圆圈内，使两个正方形中四个数之和都等于21．5.把1，2，4，5，6，11这6个数分别填入图中的○里，使每个圆圈上的四个数之和都等于22．第4级下·提高班·学生版第4级下·提高班·学生版6. 把2，5，6，8，10，12，14，22这8个数分别填入下图中，使得每个大圆上的5个数的和都等于49．思维跳板——剪指甲小华的爸爸1分钟可以剪好5个自己的指甲．那么，他在5分钟内可以剪好几个自己的指甲呢？。
三年级3数教程 数阵图2
三年级奥数教程 数阵图
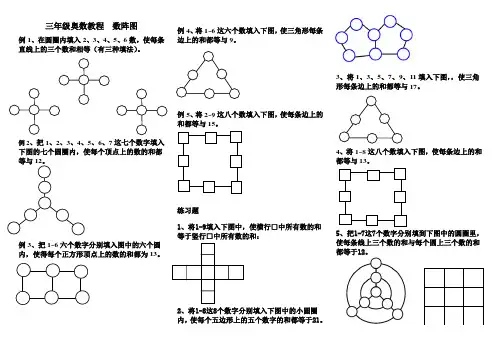
例1、在圆圈内填入2、3、4、5、6数，使每条直线上的三个数和相等（有三种填法）。
例2
、把1、2、3、4、5、6、7这七个数字填入下图的七个圆圈内，使每个顶点上的数的和都
等与12。
例3、把
1~6六个数字分别填入图中的六个圆内，使得每个正方形顶点上的数的和都为13。
例4、将
1~6这六个数填入下图，使三角形每条边上的和都等与9。
例5、将2~9这八个数填入下图，使每条边上的和都等与15。
练习题
1、将1-9填入下图中，使横行□中所有数的和等于竖行□中所有数的和：
2、将1-8这8个数字分别填入下图中的小圆圈内，使每个五边形上的五个数字的和都等于21。
3、将1、3、5、7、9、11填入下图，，使三角形每条边上的和都等与17。
4、将1~8这八个数填入下图，使每条边上的和都等与13。
5、把1-7这7个数字分别填到下图中的圆圈里，使每条线上三个数的和与每个圆上三个数的和都等于12。
三年级上奥数第16讲 数阵图(一)
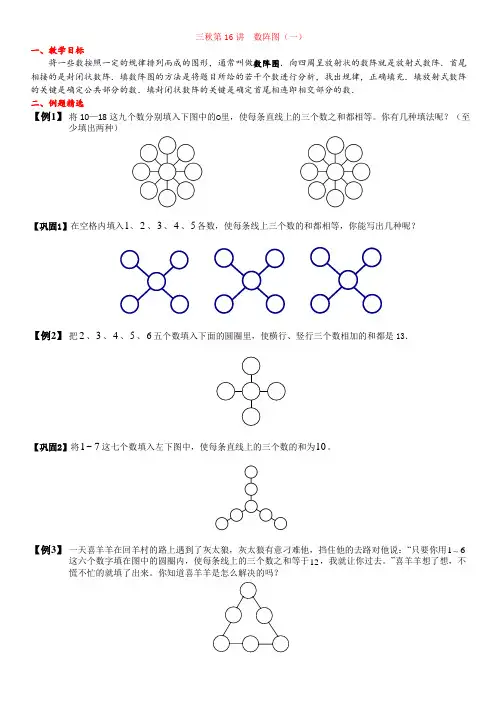
三秋第16讲 数阵图（一）一、教学目标将一些数按照一定的规律排列而成的图形，通常叫做数阵图．向四周呈放射状的数阵就是放射式数阵．首尾相接的是封闭状数阵．填数阵图的方法是将题目所给的若干个数进行分析，找出规律，正确填充．填放射式数阵的关键是确定公共部分的数．填封闭状数阵的关键是确定首尾相连即相交部分的数． 二、例题精选【例1】 将10—18这九个数分别填入下图中的○里，使每条直线上的三个数之和都相等。
你有几种填法呢？（至少填出两种）【巩固1】在空格内填入1、2、3、4、5各数，使每条线上三个数的和都相等，你能写出几种呢？【例2】 把2、3、4、5、6五个数填入下面的圆圈里，使横行、竖行三个数相加的和都是13．【巩固2】将7~1这七个数填入左下图中，使每条直线上的三个数的和为10。
【例3】 一天喜羊羊在回羊村的路上遇到了灰太狼，灰太狼有意刁难他，挡住他的去路对他说：“只要你用16这六个数字填在图中的圆圈内，使每条线上的三个数之和等于12，我就让你过去。
”喜羊羊想了想，不慌不忙的就填了出来。
你知道喜羊羊是怎么解决的吗？【巩固3】从1、2、3、4、5、6中选取适合的数填在圆圈里，使每个圆上四个数的和都等于15．【例4】将1~9这九个数分别填入下左图中，使每个三角形的顶点上的三个数的和相等。
【巩固4】将1，2，3，5，6，7这六个数填入下左表中，使每行中三个数的和相等，同时使每列两个数的和也相等。
【例5】在下左图中，三个圆圈两两相交成7块小区域，分别填上1~7这七个自然数，在一些小区域中已填好数字，请你把其余的数填到空着的小区域中，要求每个圆圈中四个数的和都是15。
375【例6】在下左列表格中填上0~8这9个数字，使得各行各列的和都恰好等于表格边上的数。
（每个数字只能用1次）21312121014。
三年级奥数1-数阵图
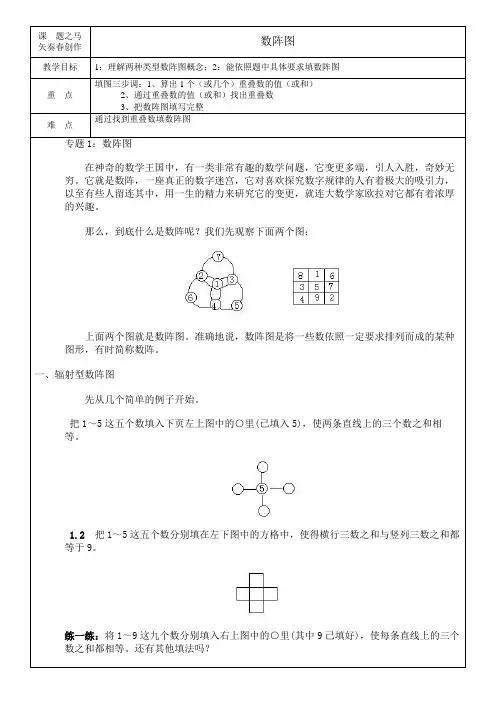
课题之马矢奏春创作数阵图教学目标1：理解两种类型数阵图概念；2：能依照题中具体要求填数阵图重点填图三步调：1、算出1个（或几个）重叠数的值（或和）2、通过重叠数的值（或和）找出重叠数3、把数阵图填写完整难点通过找到重叠数填数阵图专题1：数阵图在神奇的数学王国中，有一类非常有趣的数学问题，它变更多端，引人入胜，奇妙无穷。
它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用一生的精力来研究它的变更，就连大数学家欧拉对它都有着浓厚的兴趣。
那么，到底什么是数阵呢？我们先观察下面两个图：上面两个图就是数阵图。
准确地说，数阵图是将一些数依照一定要求排列而成的某种图形，有时简称数阵。
一、辐射型数阵图先从几个简单的例子开始。
把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。
1.2 把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。
练一练：将1～9这九个数分别填入右上图中的○里(其中9已填好)，使每条直线上的三个数之和都相等。
还有其他填法吗？例2将1～7这七个自然数填入左下图的七个○内，使得每条边上的三个数之和都等于10。
如果把例2中“每条边上的三个数之和都等于10”改为“每条边上的三个数之和都相等”，其他不变，那么仿照例1，重叠数可能等于几？怎样填？练一练：将 10～20填入左下图的○内，使得每条边上的三个数字之和都相等。
二、封闭性数阵例3将1～8这八个数分别填入右图的○中，使两个大圆上的五个数之和都等于21。
练一练：把1～8填入下页左上图的八个○里，使每个圆圈上的五个数之和都等于20。
例4 将1～6这六个自然数分别填入右图的六个○内，使得三角形每条边上的三个数之和都等于11。
将2～9这八个数分别填入右图的○里，使每条边上的三个数之和都等于18。
附加：把1～7分别填入左下图中的七个空块里，使每个圆圈里的四个数之和都等于13。
人教版小学三年级数学第讲 数阵图(一)
第16讲数阵图(一)在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。
它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。
那么，到底什么是数阵呢？我们先观察下面两个图：左上图中有3个大圆，每个圆周上都有四个数字，有意思的是，每个圆周上的四个数字之和都等于13。
右上图就更有意思了，1～9九个数字被排成三行三列，每行的三个数字之和与每列的三个数字之和，以及每条对角线上的三个数字之和都等于15，不信你就算算。
上面两个图就是数阵图。
准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵。
要排出这样巧妙的数阵图，可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了，七拼八凑就写出了右上图的答案，可是却搞不清其中的道理。
下面我们就一起来分析其中的道理，只有弄懂其中的道理，才可能解出复杂巧妙的数阵问题。
分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。
也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9，所以(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了，其余各数就好填了(见右上图)。
例2把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。
分析与解：与例1不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。
所以，必须先求出这个“和”。
根据例1的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。
三年级奥数教程第13讲 数阵图
三年级奥数教程第13讲数阵图例1、把1～6这六个数字分别填入图13一l的六个圈内，使得每个正方形顶点上的数的和都为13．分析从1到6这六个数的和是21．而两个正方形8个顶点上的数之和是26(＝13×2)，比六个数的总和大5．这是因为中间两个圈内的数，都被算了两次，所以，多出来的5就是中间两个圈内的数的和．解在1到6六个数中，两个数的和为5，只可能是1+4、2+3．当中间两个圈内填1与4时，剩下的四个数，3与5、2与6配对即可以满足条件．当中间两个圈内填2与3时，剩下的四个数无法组成和相等的两对，因而无法满足条件．所以，得到如图13—2的填法．随堂练习1将3、4、6这三个数填入图13—3的三个圆圈内，使得每条边上的三个数的和等于11．例2、将2到7这六个数，填入图13—4的圈中，使得每条线上的三个数的和相等．分析与解将三条线上的三个数都相加，中间的1被加了3次，所以三条线上三个数的和为1+2+…+6+7+1+1＝30．从而每条线上的和是10(＝30÷3)，即每条线上剩余两个圆圈内数的和是9(＝10—1)．由 2+7＝4+5＝3+6＝9．可以得到如图13—5的解．随堂练习2 将1到7这七个数填入图13—6，使得每条线上的三个数的和相等．例3、将1到9这九个数填入图13—7，使得从中心出发的每条线段上的三个数的和相等．分析与解先来确定中心的数．设这个数为a，则4条线上12个数(中心的数出现4次，其余的数各出现一次)的和1+2+…+9+a+a+a是4的倍数，即45+3×a是4的倍数．所以a只可能是1、5、9．(1)当a＝1时，2与9、4与7、8与3、5与6两两搭配填入同一条线的两个圈内即可．(2)当a＝5时，l与9、2与8、3与7、4与6搭配．(3)当a＝9时，1与8、2与7、3与6、4与5搭配．这样得到如图13—8所示的三个解．随堂练习3 将1～8填入图13—9，使两个正方形顶点上的数的和相等，并且用斜线连接的4对数的和也都相等．例4、将1到5这五个数填入图13-10，使得圆周上四个数的和与每条直线上的三个数的和都相等．分析与解设处于中心圈内的数是a，因为竖线上的三个数的和等于圆周上的四个数的和，所以a等于它左、右两个数的和．同理，a等于它上、下两个数的和．从而a是最大的数5．其余四个数，2与3搭配，1与4搭配，写在同一条线上．得到的解如图13—11所示．随堂练习4 在图13一12中圆圈内填上7、8、10、12，使得每个圆内的四个数的和相等．例5、将1～6这六个数填入图13～13的六个圆圈内，使得每条边上的三个数的和相等．分析与解用字母a、b、c表示三个顶点上的数．如果l、6都在边上，那么a、b、c中有两个数的差是5(＝6—1)．这不可能．所以可设以a＝1或6．如果a＝1，那么由2+6＝3+5．3+6＝4+5．可得图13—14的(1)，(2)．如果a＝6，同样可得图13—14的 (3)，(4)．随堂练习5 将l到16填入图13—15，使得每条线段上四个数的和相等，两个八边形八个顶点上的数的和也相等．例6、将1～16填入图13—16的正方形，使每行、每列、每条对角线的和都相等．图13—16分析与解本题也就是造一个四阶幻方．四阶幻方的造法很多，解也不惟一．下面介绍一种最简的做法，可以称为调整法．先将1～16依照次序先左后右，先上后下逐一填入图13—17(1)中得1234114154115144 567896712126799101112510118810115 13141516132316133216⑴⑵⑶图13—17四阶幻方中每行和、每列和、每条对角线的和都是 (1+2+…+16)÷4＝(1+16)×16÷2÷4＝34．现在图13—17(1)的两条对角线的和都已经是34，合乎要求．所以对角线上的数不要再动．先来调整行．将第一行的2、3分别与第四行的14、15对调，第二行的5、8分别与第三行的9、12对调，得图13—17(2)，这个图中，不但每条对角线的和是34，每一行的和也都是34．再调整列．将图13—17(2)第一列的9、5分别与第四列的12、8对调，第二列的14、2分别与15、3对调，得图13—17(3)，这个图就是一个合乎要求的幻方．随堂练习6 比较例6所得的幻方与随堂练习5的答案．有何联系?读一读……………………………………………………可能与必然上节末，说到一个游戏“数独”．数独怎么填呢?比如先看第一行，在上节末的图中，有6个空格，应填1、2、4、7、8、9这6个数字．每个空格填的数有6种可能，难以确定．如果看第二列，只有2个空格，应填2、7，每个空格有2种可能，但还不能惟一确定．可能性太多，需要逐个枚举讨论，比较麻烦．所以应先考虑可能较小的方格．最好能发现一些方格，只有一种填法，也就是说这些方格填什么数是必然的．将这些方格先填好，对填其他方格会有帮助．同时考虑几个方面的要求，可以得到必然的填法．比如中间的3×3的正方形，只有3个空格，应填2、6、8．再结合第四行已经有8，第六行也已经有8，所以8必须填在中央．接下去，因为第四行已经有6，所以6必须填在第六行，2填在第四行．现在再看第四行，只剩2个空格，应填9与3．第九列有9，所以第四行的9只能(必然)在第三列，3在第九列．同样，右中3×3的正方形中，9必然在第六行．第六行第一列必填2．左中3×3的正方形中，5必在第一列，7在第三列．第八列3必填在第九行，9必填在第二行．右上3×3的正方形中，7必填在第七列．右下3×3的正方形中，5必在第八行第七列，2必在第八行，1在第九列第七行，6在第七行第七列．右中3×3的正方形中，6在第九列，2在第七列．左下3×3的正方形中，2、3、8、6的填法都是必然的．左上3×3的正方形中，按行依次填2、1、4、7、6．右上3×3的正方形中，填4、8．中上3×3的正方形中填8、9、6、2、7、4．中下3×3的正方形中填9、3、6、4、1、7．填法都是必然的。
(完整)小学三年级奥数--数阵图
数阵图（一）在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。
它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。
那么，到底什么是数阵呢？我们先观察下面两个图：左上图中有3个大圆，每个圆周上都有四个数字，有意思的是，每个圆周上的四个数字之和都等于13。
右上图就更有意思了，1～9九个数字被排成三行三列，每行的三个数字之和与每列的三个数字之和，以及每条对角线上的三个数字之和都等于15，不信你就算算。
上面两个图就是数阵图。
准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵。
要排出这样巧妙的数阵图，可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了，七拼八凑就写出了右上图的答案，可是却搞不清其中的道理。
下面我们就一起来分析其中的道理，只有弄懂其中的道理，才可能解出复杂巧妙的数阵问题。
分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。
也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9，所以(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3。
重叠数求出来了，其余各数就好填了(见右上图)。
试一试：练习与思考第1题。
例2把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等。
分析与解：与例1不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。
所以，必须先求出这个“和”。
根据例1的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[(1+2+3+4+5)+5]÷2=10。
(完整版)小学三年级奥数--数阵图
数阵图(一)在神奇的数学王国中，有一类非常有趣的数学问题，它变化多端，引人入胜，奇妙无穷。
它就是数阵，一座真正的数字迷宫，它对喜欢探究数字规律的人有着极大的吸引力，以至有些人留连其中，用毕生的精力来研究它的变化，就连大数学家欧拉对它都有着浓厚的兴趣。
那么，到底什么是数阵呢？我们先观察下面两个图：左上图中有3个大圆，每个圆周上都有四个数字，有意思的是，每个圆周上的四个数字之和都等于13。
右上图就更有意思了，1～9 九个数字被排成三行三列，每行的三个数字之和与每列的三个数字之和，以及每条对角线上的三个数字之和都等于15，不信你就算算。
上面两个图就是数阵图。
准确地说，数阵图是将一些数按照一定要求排列而成的某种图形，有时简称数阵。
要排出这样巧妙的数阵图，可不是一件容易的事情。
我们还是先从几个简单的例子开始。
例1 把1～5这五个数分别填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9。
同学们可能会觉得这道题太容易了，七拼八凑就写出了右上图的答案，可是却搞不清其中的道理。
下面我们就一起来分析其中的道理，只有弄懂其中的道理，才可能解出复杂巧妙的数阵问题。
分析与解：中间方格中的数很特殊，横行的三个数有它，竖列的三个数也有它，我们把它叫做“重叠数”。
也就是说，横行的三个数之和加上竖列的三个数之和，只有重叠数被加了两次，即重叠了一次，其余各数均被加了一次。
因为横行的三个数之和与竖列的三个数之和都等于9，所以(1+2+3+4+5)+重叠数=9+9，重叠数=(9+9)-(1+2+3+4+5)=3 。
重叠数求出来了，其余各数就好填了（见右上图）。
试一试：练习与思考第1 题。
例2 把1～5 这五个数填入下页左上图中的○里（已填入5），使两条直线上的三个数之和相等。
分析与解：与例1 不同之处是已知“重叠数”为5，而不知道两条直线上的三个数之和都等于什么数。
所以，必须先求出这个“和”。
根据例1 的分析知，两条直线上的三个数相加，只有重叠数被加了两遍，其余各数均被加了一遍，所以两条直线上的三个数之和都等于[（1+2+3+4+5）+5] ÷2=10。
小学奥数模块教程数阵图
数阵图是小学奥数阶段一个很重要的专题。
在这节课中，我们的教学目标就是让学生初步认识数阵，并能通过一系列的练习，找到解数阵的一般方法。
今天我们重点研究的方法，就是通过找中心数来解题，会根据题目中给出的已知条件来求中心数。
在例题的设计中，我们也是层层深入，让学生能通过简单的例题来发现规律找到解题的方法，通过例题难度的加深来拓展应用。
希望这节课的学习能使学生的思维能力得到培养，能让学生对数阵产生兴趣，为今后的继续学习奠定基础。
在神奇的数学王国里，有一类非常有趣的数学问题，它变化多端，引人入胜， 奇妙无穷．它就是数阵图．到底什么是数阵图呢？我们先观察下面两个图：数阵图就是将一些数按照一定要求排列而成的某种图形．它一般分为辐射型(图1)和封闭型(2)两种．要把一些数字按一定的规则填入图形中，并不是一件容易的事，这需要我们多观察，找关系，仔细推理才能完成．下面我们就一起来找一找数阵图的秘密吧【例1】 把1，2，3，4，5这 5个数分别填入图中的圆圈内，（1）使得横行 3个数的和与竖列 3个数的和都等于10。
（2）使得横行3个数的和与竖列3个数的和都相等.一共有多少种不同的填法？【例2】 把4～8这五个数填入图中(已填入6)，使两条直线上的三个数之和相等.例题精讲知识框架数阵图 巧求周长【例3】把1，2，3，4，5，6，7 这7个数分别填入圆圈中，使得每条直线上的3个数的和等于12．【例4】把1～9这九个数字填入下列圆圈内，使每条线上的三个圆圈内的数之和都等于15。
【例5】1～7这七个数分别填入图中的各○内，使每条直线上三个○里数的和相等．一共有多少种方法？【例6】把1～9这9个数分别填入下图的圆圈中，使得每条直线上的3个数的和都等于15。
【例7】将1，2，3，4，5，6这6个数分别填入下图中，使两个大圆上4个数的和都等于14.【例8】 把1，2，3，4，5，6这6个数分别填入右图的6个圆圈中，（1）使得三角形每条边上的3个数的和都等于10.（2）使得三角形每条边上的三个数之和都相等.还有几种不同的填法？【例9】 将1、2、3、4、5、6、7、8、9这9个数字分别填入图中的小圆圈里，使得每条边上4个数字的和是17.【例10】把1～8这八个数分别填入图中的圆内，使每条线上的三个数相加的和等于12.【随练1】 将1、2、3、4、5、6六个数填在图中的空灯里，使每个大圆上的四盏灯里的数相加都等于14.【随练2】 把2、3、4、5、6、7、8、9、10填入方格里，使每一横行、每一竖行、每一斜行的3个数的和都是18.课堂检测【作业1】 在下面的○里填上适当的数，使每条线上的三个数之和都是16.【作业2】 在空格内填入适当的数，使得每行、每列和两条对角线上的三个数的和都为18.【作业3】 在空格内填上适当的数，使得图中每行、每列及两对角线上四个数的和都是64.【作业4】 把数字1、2、3、4、5分别填入下图中的方格内，使横行3个数的和与竖列3个数的和都等于9.【作业5】 把5，6，7，8，9这5个数填在下图的◇内，使横行、竖列3个数的和都相等.【作业6】 将1～9填入小方格里，使横行和竖列上五个数之和相等.家庭作业【作业7】把10，20，30，40，50，60，70这7个数填在圆圈里，使每条直线上和每个圆周上的三个数的和都是120.【作业8】把3、5、7、9、11、13、15这7个数分别填入图中的圆圈内，使每条直线上的3个数都等于27.【作业9】把1～6填入○里，使每个圆圈上的四个数之和都相等16.【作业10】把4～9这6个数分别填入下图的6个圆圈中，使得三角形每条边上的3个数的和都等于21.。
学而思教材目录
学而思教材目录一年级寒假班：第一讲：突破加减竖式第二讲：巧填算符初步第三讲：剪拼图形第四讲：图文代换第五讲：巧移物体第六讲：左右脑开发3（逻辑推理）第七讲：期末测评二年级寒假班：第一讲：认识倍第二讲：带余除法初步第三讲：有趣的自然数串第四讲：分割图像第五讲：枚举法的妙用第六讲：鸡兔同笼初步第七讲：期末测评三年级寒假班：第一讲：角度初识第二讲：速算与巧算之四则运算第三讲：字母表示数第四讲：和差倍第五讲：倒退与图示第六讲：方阵第七讲：期末测评三年级春季班：第一讲：巧填算符第二讲：小数的认识第三讲：平行四边形与梯形第四讲：年龄问题第五讲：带余除法初步第六讲：简单统计第七讲：图形计数初步第八讲：组合中的点线关系第九讲：等差数列初步第十讲：页码问题第十一讲：标数法第十二讲：简易方程第十三讲：简易方程应用第十四讲：路程速度与时间第十五讲：期末测评四年级暑假班：第一讲：简单抽屉原理第二讲：奇数和偶数第三讲：二次相遇问题第四讲：应用题：假设法和还原法（鸡兔同笼，还原问题，方阵综合应用）第五讲：应用题：图示法和对应法（年龄，盈亏，平均数综合）第六讲：图形计数进阶第七讲：余数和周期第八讲：四边形中的基本图形第九讲：体育比赛中的数学第十讲：期末测评四年级秋季班：第一讲：定义新运算第二讲：体育比赛中的数学问题第三讲：图形计数进阶第四讲：多位数计算第五讲：等积变型第六讲：一半模型第七讲：最值问题初步第八讲：数阵图初步—从幻方谈起第九讲：平均数进阶第十讲：破译乘除法竖式第十一讲：方程和方程组第十二讲：方程组解应用题第十三讲：环形跑道第十四讲：火车过桥第十五讲：期末测评四年级寒假班：第一讲：小数巧算第二讲：格点与割补第三讲：数表从日历谈起第四讲：第五种运算（乘方的认识，运算性质，平方差认识）第五讲：质数合数初步第六讲：包含与排除第七讲：期末测评四年级春季班：第一讲：等积变形第二讲：整数与数列第三讲：统筹和最优化第四讲：加乘原理进阶第五讲：最值问题进阶第六讲：抽屉原理初步第七讲：流水行船第八讲：方程与方程组第九讲：一半模型第十讲：相遇与追及综合第十一讲：平移、选择和对称第十二讲：破译横式（奇偶分析，枚举试算）第十三讲：进位制初步第十四讲：数阵图进阶第十五讲：期末测评五年级暑假班：第一讲：分数乘除第二讲：分数加减第三讲：棋盘中的数学第四讲：枚举法进阶。
三年级奥数1-数阵图
课题之羊若含玉创作数阵图教授教养目的1：懂得两种类型数阵图概念；2：能依照题中具体要求填数阵图重点填图三步调：1、算出1个（或几个）重叠数的值（或和）2、通过重叠数的值（或和）找出重叠数3、把数阵图填写完整难点通过找到重叠数填数阵图专题1：数阵图在神奇的数学王国中，有一类异常有趣的数学问题，它变更多端，引人入胜，奇妙无穷.它就是数阵，一座真正的数字迷宫，它对喜欢探究数字纪律的人有着极大的吸引力，以至有些人留连其中，用一生的精神来研究它的变更，就连大数学家欧拉对它都有着浓重的兴趣.那么，到底什么是数阵呢？我们先不雅察下面两个图：上面两个图就是数阵图.准确地说，数阵图是将一些数依照一定要求分列而成的某种图形，有时简称数阵.一、辐射型数阵图先从几个简略的例子开端.把1～5这五个数填入下页左上图中的○里(已填入5)，使两条直线上的三个数之和相等.1.2 把1～5这五个数分离填在左下图中的方格中，使得横行三数之和与竖列三数之和都等于9.练一练：将1～9这九个数分离填入右上图中的○里(其中9已填好)，使每条直线上的三个数之和都相等.还有其他填法吗？例2将1～7这七个自然数填入左下图的七个○内，使得每条边上的三个数之和都等于10.如果把例2中“每条边上的三个数之和都等于10”改为“每条边上的三个数之和都相等”，其他不变，那么模仿例1，重叠数可能等于几？怎样填？练一练：将 10～20填入左下图的○内，使得每条边上的三个数字之和都相等.二、关闭性数阵例3将1～8这八个数分离填入右图的○中，使两个大圆上的五个数之和都等于21.练一练：把1～8填入下页左上图的八个○里，使每个圆圈上的五个数之和都等于20.例4 将1～6这六个自然数分离填入右图的六个○内，使得三角形每条边上的三个数之和都等于11.将2～9这八个数分离填入右图的○里，使每条边上的三个数之和都等于18.附加：把1～7分离填入左下图中的七个空块里，使每个圆圈里的四个数之和都等于13.你学会了吗1.将3～9这七个数分离填入下图的○里，使每条直线上的三个数之和等于20.2.将1～11这十一个数分离填入图的○里，使每条直线上的三个数之和相等，并且尽可能大.3、把5、6、7、8、9、10、11、12、12、14填入下图，使每个大圆圈中六个数的和是554.将1～8填入左下图的八个○中，使得每条边上的三个数之和都等于15.作业：1、将1～9这九个数分离填入右图的小方格里，使横行和竖列上五个数之和相等.(有若干种填法？)2、把1～6这六个数填入右上图的○里，使每个圆圈上的四个数之和都相等.3、将4、5、6、7、8、9六个数填在下图，使每条边上得三个数之和都相等，并且和为最大，和为最小呢？4、把1——7这7个数，分离填入途中，使直线和大圆上的数之和相等生活趣题：小猫要把15条鱼分成数量不相等的4堆，问最多的一堆中最多可放几条鱼？。
三年级奥数：数阵图(2)动态课件
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字 之和等于竖列的四个数字之和。
652 4 3 1
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字 之和等于竖列的四个数字之和。
＋1＋2＋3＋4＋5＋6 = 212
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字 之和等于竖列的四个数字之和。
1＋2＋3＋4＋5＋6 = 214
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字 之和等于竖列的四个数字之和。
1＋2＋3＋4＋5＋6 = 261
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字 之和等于竖列的四个数字之和。
1＋2＋3＋4＋5＋6 = 21
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字 之和等于竖列的四个数字之和。
56
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字 之和等于竖列的四个数字之和。
654 3 2 1
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字 之和等于竖列的四个数字之和。
之和等于竖列的四个数字之和。 1+2+3+4+5+6=21
六个数字之和： 21
（单）
= 三个数字 四个数字
七个数字之和：双
将1、2、3、4、5、6 分别填入6个方块内使得横行的三个数字
之和等于竖列的四个数字之和。 1+2+3+4+5+6=21
六个数字之和： 21
（单）
= 三个数字 四个数字
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
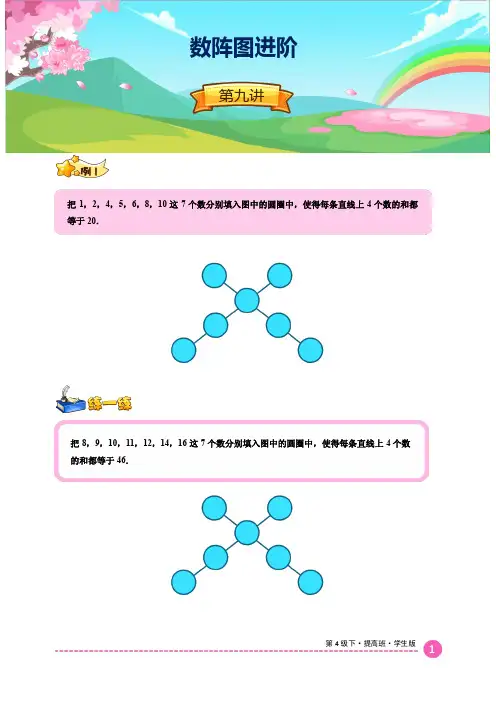
把8，9，10，11，12，14，16这7个数分别填入图中的圆圈中，使得每条直线上4个数的和都等于46．
把1，2，4，5，6，8，10这7个数分别填入图中的圆圈中，使得每条直线上4个数的和都等于20．
数阵图进阶
第九讲
第4级下·提高班·学生版
第4级下·提高班·学生版
把2，3，4，5，6，7，8这七个数分别填入图中的圆圈中，使两个正方形中四个数之和都等于19． 将5，9，13，14，17，21，25这7个数分别填入图中的圆圈中，使得每条直线上3个数的和都等于44．
第4级下·提高班·学生版
将5，6，9，11，14，15这6个数分别填入图中的圆圈里，使两个大圆上4个数的和都等于40．
把1，5，9，10，16，21这6个数分别填入图中的○里，使每一个大圆上的四个数之和都等于36．
第4级下·提高班·学生版
1． 把5，6，7，8，9这5个数分别填在下图的
内，使横行、竖列3个数的和都等于( )中的
数．
把1，3，4，5，6，8，11，15这8个数分别填入图中的圆圈里，使得每个大圆上5个数的和都等于33．
第4级下·提高班·学生版
2. 把3，5，7，9，11，13，15这7个数分别填入图中的圆圈内，使每条直线上的3个数的和都等于
27．
3. 把2，4，6，8，10，12，14，16，18这9个数分别填入下图的圆圈中，使得每条直线上的3个数
的和都等于24．
4.把2，3，4，5，6，7，8这七个数分别填入图中的圆圈内，使两个正方形中四个数之和都等于21．
5.把1，2，4，5，6，11这6个数分别填入图中的○里，使每个圆圈上的四个数之和都等于22．
第4级下·提高班·学生版
第4级下·提高班·学生版
6. 把2，5，6，8，10，12，14，22这8个数分别填入下图中，使得每个大圆上的5个数的和都等于
49．
思维跳板——剪指甲
小华的爸爸1分钟可以剪好5个自己的指甲．那么，他在5分钟内可以剪好几个自己的指甲呢？。