计量经济学第2章回归与回归分析
计量经济学复习要点

计量经济学复习要点参考教材:李子奈 潘文卿 计量经济学 数据类型:截面、时间序列、面板第二章 简单线性回归回归分析的基本概念,常用术语现代意义的回归是一个被解释变量对若干个解释变量依存关系的研究,回归的实质是由固定的解释变量去估计被解释变量的平均值;简单线性回归模型是只有一个解释变量的线性回归模型; 回归中的四个重要概念1. 总体回归模型Population Regression Model,PRMt t t u x y ++=10ββ--代表了总体变量间的真实关系;2. 总体回归函数Population Regression Function,PRFt t x y E 10)(ββ+=--代表了总体变量间的依存规律;3. 样本回归函数Sample Regression Function,SRFtt t e x y ++=10ˆˆββ--代表了样本显示的变量关系; 4. 样本回归模型Sample Regression Model,SRMtt x y 10ˆˆˆββ+=---代表了样本显示的变量依存规律; 总体回归模型与样本回归模型的主要区别是:①描述的对象不同;总体回归模型描述总体中变量y 与x 的相互关系,而样本回归模型描述所关的样本中变量y 与x 的相互关系;②建立模型的依据不同;总体回归模型是依据总体全部观测资料建立的,样本回归模型是依据样本观测资料建立的;③模型性质不同;总体回归模型不是随机模型,而样本回归模型是一个随机模型,它随样本的改变而改变;总体回归模型与样本回归模型的联系是:样本回归模型是总体回归模型的一个估计式,之所以建立样本回归模型,目的是用来估计总体回归模型;线性回归的含义线性:被解释变量是关于参数的线性函数可以不是解释变量的线性函数线性回归模型的基本假设简单线性回归的基本假定:对模型和变量的假定、对随机扰动项u 的假定零均值假定、同方差假定、无自相关假定、随机扰动与解释变量不相关假定、正态性假定 普通最小二乘法原理、推导最小二乘法估计参数的原则是以“残差平方和最小”; Min21ˆ()niii Y Y =-∑01ˆˆ(,)ββ: 1121()()ˆ()nii i n ii XX Y Y XX ==--β=-∑∑ , 01ˆˆY Xβ=-βOLS 估计量的性质1线性:是指参数估计值0β和1β分别为观测值t y 的线性组合; 2无偏性:是指0β和1β的期望值分别是总体参数0β和1β; 3最优性最小方差性:是指最小二乘估计量0β和1β在在各种线性无偏估计中,具有最小方差; 高斯-马尔可夫定理OLS 参数估计量的概率分布OLS 随机误差项μ的方差σ2的估计 拟合优度的检验R 2 离差平方和的分解:TSS=ESS+RSS“拟合优度”是模型对样本数据的拟合程度;检验方法是构造一个可以表征拟合程度的指标——判定系数又称决定系数;121SSE SST SSR SSRR SST SST SST-===-,表示回归平方和与总离差平方和之比;反映了样本回归线对样本观测值拟合优劣程度的一种描述; 2 2[0,1]R ∈;3 回归模型中所包含的解释变量越多,2R 越大变量显着性检验,t 检验例子:回归报告函数形式对数、半对数模型系数的解释101ˆˆˆi iY X =β+β:X 变化一个单位Y 的变化 2^22()i Var x σβ=∑2^22ie n σ=-∑201ˆˆˆln ln i i Y X =β+β: X 变化1%,Y 变化1ˆβ%,表示弹性; 301ˆˆˆln i i Y X =β+β:X 变化一个单位,Y 变化百分之1001ˆβ 401ˆˆˆln i iY X =β+β:X 变化1%,Y 变化1ˆβ/100; 第三章 多元线性回归1、变量系数的解释剔除、控制其他因素的影响对斜率系数1ˆβ的解释:在控制其他解释变量X2不变的条件下,X1变化一个单位对Y 的影响;或者,在剔除了其他解释变量的影响之后,X1的变化对Y 的单独影响2、多元线性回归模型中对随机扰动项u 的假定,除了零均值假定、同方差假定、无自相关假定、随机扰动与解释变量不相关假定、正态性假定以外,还要求满足无多重共线性假定;3、多元线性回归模型参数的最小二乘估计式;参数估计式的分布性质及期望、方差和标准误差;在基本假定满足的条件下,多元线性回归模型最小二乘估计式是最佳线性无偏估计式;最小二乘法 OLS 公式: Y ' X X)' (X ˆ-1=β估计的回归模型: 的方差协方差矩阵: 残差的方差 : βˆ的估计的方差协方差矩阵是:4、修正可决系数的作用和方法;5、F 检验是对多元线性回归模型中所有解释变量联合显着性的检验,F 检验是在方差分析基础上进行的; 6、t检验7、可化为线性回归的模型 8、约束回归第四章 放宽基本假设一、异方差什么是异方差 异方差的后果ˆˆY =X β+u βˆ2ˆˆ'uu n k -s =异方差的检验White 检验 异方差的处理 加权最小二乘法 异方差稳健标准误二、序列相关什么是序列相关 序列相关的后果序列相关的检验DW 检验、LM 检验 序列相关的处理 广义最小二乘法 Newey-West 稳健标准误三、多重共线性多重共线性的概念 多重共线性的后果 多重共线性的检验 多重共线性的处理四、工具变量什么时候需要工具变量 作为工具变量的条件 两阶段最小二乘法第五章 专门问题一、虚拟变量1. 虚拟变量的定义:定性变量二值与多值;虚拟变量有时候不一定只是0和1;2. 如何引入虚拟变量:如果一个变量分成N 组,引入该变量的虚拟变量形式是只能放入N-1个虚拟变量;3. 虚拟变量系数的解释:不同组均值的差基准组或对照组与处理组4. 以下几种模型形式表达的不同含义;1tt t t u D X Y +++=210βββ:截距项不同;2tt t t t u X D X Y +++=210βββ:斜率不同;3tt t t t t u X D D X Y ++++=3210ββββ:截距项与斜率都不同;其中D 是二值虚拟变量,X 是连续的变量;第八章 时间序列平稳性的概念 白噪声 随机游走 单位根的概念单位根的检验ADF 检验,ADF 的三种形式 单整趋势平稳与差分平稳 协整的概念 协整的检验 误差修正模型Eviews 回归结果界面解释表计量经济学复习题第二章习题:1、2、3、5、6、7、9、10、11、12第三章习题:1、2、3、4、5、6、7、8、9、10、11、12、13 第四章习题:2、5、6、8、9、10 第五章习题:1、2、3、5、6 第八章习题:1、2、5、6、7、8 1、判断下列表达式是否正确 2、给定一元线性回归模型:1叙述模型的基本假定;2写出参数0β和1β的最小二乘估计公式; 3说明满足基本假定的最小二乘估计量的统计性质; 4写出随机扰动项方差的无偏估计公式; 3、对于多元线性计量经济学模型:1该模型的矩阵形式及各矩阵的含义; 2对应的样本线性回归模型的矩阵形式; 3模型的最小二乘参数估计量;4、根据美国1961年第一季度至1977年第二季度的数据,我们得到了如下的咖啡需求函数的回归方程:D D D P I P t t t t t t tT Q 321'0097.0157.00961.00089.0ln 1483.0ln 5115.0ln 1647.02789.1ˆln ----++-=其中,Q=人均咖啡消费量单位:磅;P=咖啡的价格以1967年价格为不变价格;I=人均可支配收入单位:千元,以1967年价格为不变价格;P '=茶的价格1/4磅,以1967年价格为不变价格;T=时间趋势变量1961年第一季度为1,…,1977年第二季度为66;D 1=1:第一季度;D 2=1:第二季度;D 3=1:第三季度; 请回答以下问题:① 模型中P 、I 和P '的系数的经济含义是什么 ② 咖啡的需求是否很有弹性 ③ 咖啡和茶是互补品还是替代品④ 你如何解释时间变量T 的系数 ⑤ 你如何解释模型中虚拟变量的作用 ⑥ 哪一个虚拟变量在统计上是显着的 ⑦ 咖啡的需求是否存在季节效应5、为研究体重与身高的关系,我们随机抽样调查了51名学生其中36名男生,15名女生,并得到如下两种回归模型:h W5662.506551.232ˆ+-= t=h D W7402.38238.239621.122ˆ++-= t=其中,Wweight=体重 单位:磅;hheight=身高 单位:英寸 请回答以下问题:① 你将选择哪一个模型为什么② 如果模型确实更好,而你选择了,你犯了什么错误 ③ D 的系数说明了什么6、以t Q 表示粮食产量,t A 表示播种面积,t C 表示化肥施用量,经检验,它们取对数后都是)1(I 变量且互相之间存在)1,1(CI 关系;同时经过检验并剔除不显着的变量包括滞后变量,得到如下粮食生产模型:t t t t t t C C A Q Q μααααα+++++=--1432110ln ln ln ln ln 1 ⑴ 写出长期均衡方程的理论形式; ⑵ 写出误差修正项ecm 的理论形式; ⑶ 写出误差修正模型的理论形式;⑷ 指出误差修正模型中每个待估参数的经济意义;7、简述异方差对下列各项有何影响:1OLS 估计量及其方差;2置信区间;3显着性t 检验和F 检验的使用;8、假设某研究使用250名男性和280名女性工人的工资Wage 数据估计出如下OLS 回归:标准误其中WAGE 的单位是美元/小时,Male 为男性=1,女性=0的虚拟变量;用男性和女性的平均收入之差定义工资的性别差距;1性别差距的估计值是多少2计算截距项和Male系数的t统计量,估计出的性别差距统计显着不为0吗5%显着水平的t统计量临界值为3样本中女性的平均工资是多少男性的呢4对本回归的R2你有什么评论,它告诉了你什么,没有告诉你什么评价这个回归结果5另一个研究者利用相同的数据,但建立了WAGE对Female的回归,其中Female 为女性=1,男性=0的变量;由此计算出的回归估计是什么9、基于人口调查1998年的数据得到平均小时收入对性别、教育和其他特征的回归结果,见下表;其中:AHE=平均小时收入;College=二元变量大学取1,高中取0;Female女性取1,男性取0;Age=年龄年;Northeast居于东北取1,否则为0;Midwest居于中西取1,否则为0;South居于南部取1,否则为0;West居于西部取1,否则取0;表1:基于2004年CPS数据得到的平均小时收入对年龄、性别、教育、地区的回归结果概括统计量和联合检验SERR2注:括号中是标准误;(1)计算每个回归的调整R2;(2)利用表1中列1的回归结果回答:大学毕业的工人平均比高中毕业的工人挣得多吗多多少这个差距在5%显着性水平下统计显着吗男性平均比女性挣的多吗多多少这个差距在5%显着性水平下统计显着吗(3)年龄是收入的重要决定因素吗请解释;使用适当的统计检验来回答;(4)Sally是29岁女性大学毕业生,Betsy是34岁女性大学毕业生,预测她们的收入;(5)用列3的回归结果回答:地区间平均收入存在显着差距吗利用适当的假设检验解释你的答案;(6)为什么在回归中省略了回归变量West如果加上会怎样;解释3个地区回归变量的系数的经济含义;7Juantia是南部28岁女性大学毕业生,Jennifer是中西部28岁女性大学毕业生,计算她们收入的期望差距。
计量经济学中的回归分析方法

计量经济学中的回归分析方法计量经济学是经济学中的一个重要分支,它主要是利用经济数据来进行定量分析。
而对于计量经济学来说,最重要的方法之一就是回归分析。
回归分析方法可以用来寻找变量之间的关系,进而预测未来的趋势和结果。
本文将介绍回归分析方法的基本原理及其在计量经济学中的应用。
回归分析的基本原理回归分析是一种利用数据来寻找变量之间关系的方法,其核心原理是利用多元线性回归模型。
多元线性回归模型可以描述多个自变量与一个因变量之间的关系,如下所示:Y = β0 + β1X1 + β2X2 + … + βkXk + ε其中,Y表示因变量,即需要预测的变量;X1、X2、 (X)表示自变量,即可以通过对它们的变化来预测Y的变化;β0、β1、β2、…、βk表示模型中的系数,它们可以反映每个自变量对因变量的影响;ε表示误差项,即预测结果与真实值之间的差异。
利用回归分析方法,我们可以通过最小化误差项来得到最佳的系数估计值,从而建立一个能够准确预测未来趋势和结果的模型。
回归分析的应用在计量经济学中,回归分析被广泛应用于各个领域。
下面我们以宏观经济学和微观经济学为例,来介绍回归分析在计量经济学中的具体应用。
1. 宏观经济学:用回归分析预测国内生产总值(GDP)国内生产总值是一个国家经济发展的重要指标,因此预测GDP 的变化是宏观经济学研究的重点之一。
在这个领域,回归分析可以用来寻找各种经济因素与GDP之间的关系,进而通过对这些因素的预测来预测GDP的变化。
例如,我们可以通过回归分析来确定投资、消费、进出口等因素与GDP之间的关系,进而利用这些关系来预测未来的GDP变化。
2. 微观经济学:用回归分析估算价格弹性在微观经济学中,回归分析可以用来估算价格弹性。
价格弹性可以衡量消费者对价格变化的敏感度,其计算公式为:价格弹性= %Δ数量÷ %Δ价格例如,如果价格变化1%,相应数量变化1.5%,那么价格弹性就是1.5 ÷ 1 = 1.5。
第2章计量经济学回归分析的性质ppt课件

§2.4 数据
一、数据的分类 按照数据与时间的关系,可以分为: ❖ 时间序列数据(time series data) ❖ 横截面数据(cross-section data) ❖ 面板数据(panel data/ pooling data)
实例:我国地区的生产总值
二、数据的来源和质量
❖ 社会科学数据都是非实验所得,存在测量误 差,或出于疏漏或差错 ;
cov(Xt,Yt)
Var(Xt) Var(Yt)
样本相关系数r
rXYˆ
1 T1
(Xt X)(Yt Y)
1 T1
(Xt X)2
1 T1
(Yt Y)2
(Xt X)(Yt Y)
(Xt X)2 (Yt Y)2
性质: (1)r具有对称性 (2)r与原点和尺度都无关
400
200
0 0
X
10
20
30
40
50
完全相关
Y 2
1
X
0
10
20
30
40
50
高度相关
3.0
2.5
Y
2.0
1.5
1.0
0.5
2.0
2.5
3.0
3.5
弱相关
X
4.0
4.5
4
Y 2
0
-2
X -4
-4
-2
0
2
4
零相关
2、按变量个数
200 150 100
50 0 0
Y
X
50
100
150
200
250
非线性相关/负相关
Y 2
1
第二章 双变量回归分析(计量经济学,南开大学)
ˆ 和 ˆ 1 2
i
为Yi的线性函数
i 2 i
ˆ
2
xY x
(
xi )Yi 2 x i
k Y
i
i
其中k i
xi xi2 1 xi2
ki k i2
x
2
i
0
2 xi
1 xi2 1 xi2
i
1 xi2
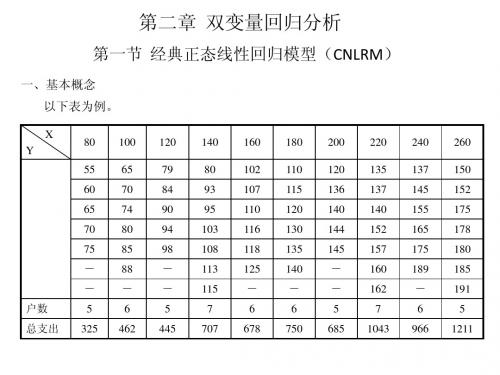
6、样本回归函数(SRF) 由于在大多数情况下,我们只知道变量值得一个样本,要用样本信息的基础 上估计PRF。(表) 样本1
X(收入) Y(支出) 80 55 100 65 120 79 140 80 160 102 180 110 200 120 220 135 240 137 260 150
样本2
ˆ ) VAR( 2
x
2 i
2
2 i
x
ˆ: 对于 1
ˆ Y ˆ X 1 ˆ X Yi 1 2 2 n 1 ˆ X ( 1 2 X i ui ) 2 n u 1 i X k i ui n ˆ ) E[( ui X 方差:VAR( k i ui ) 2 ] 1 n
ˆ ) E( ki E (ui ) 2 2 2 ˆ Y ˆ X 1 2 ( 1 2 X i ui ) ( 1 k i u i ) X 1 u i X k i u i ˆ ) E( 1 1
1 1 2 21
估计量(Estimator):一个估计量又称统计量(statistic),是指一个规则、公式 或方法,以用来根据已知的样本所提供的信息去估计总体参数。在应用中,由估 计量算出的数值称为估计(值)(estimate)。 样本回归函数SRF的随机形式为:
第2章(回归分析)

§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1.总体回归模型 总体回归模型 对应不同收入水平的60户家庭的每周消费 户家庭的每周消费Y 对应不同收入水平的 户家庭的每周消费
200 160
120
80
40 60 80 100 120 140 160 180 200 220 240 260 280
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
§2.1 总体与总体回归模型
二.总体回归模型中的 Ui 所包含的内容 2.从实际经济行为看 从实际经济行为看Ui 从实际经济行为看
Yi = E (Y X i ) + U i = β 0 + β1 X i + U i
从经济学理论可知, 除收入X外 家庭财富、 从经济学理论可知 除收入 外,家庭财富、 通胀、利率, 通胀、利率,预期等对消费支出产生影响的因 包含在U之中 素,包含在 之中
§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1. 总体 2. 总体回归模型 二、总体回归模型中 ui所包含的内容 1.从数量上看 ui 从数量上看 2.从实际经济行为看 ui 从实际经济行为看 3.从回归关系看 ui 从回归关系看
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
家庭每周收入X 家庭每周收入
《计量经济学》王少平 杨继生 欧阳志刚 高教出版社 2010.6
§2.1 总体与总体回归模型
一、总体与总体回归模型的含义 1.总体回归模型 总体回归模型
上图说明,收入 从 变化至 变化至280,这一变化 上图说明,收入X从80变化至 说明 , 解释了消费Y的总体的条件期望 均值) 的总体的条件期望( 解释了消费 的总体的条件期望(均值)从65、 、 89等变化至 等变化至173。也就是说,X的变化解释了 等变化至 。也就是说, 的变化解释了 Y的总体的条件期望的变化(总体的平均变 的总体的条件期望的变化( 的总体的条件期望的变化 )。或者说 或者说, 的变化 决定了Y的总体的 的变化, 化)。或者说,X的变化,决定了 的总体的 平均变化。 的变化解释( 平均变化。而X的变化解释(或决定)了Y 的 的变化解释 或决定) 总体的平均变化,这正是回归分析的意义所在。 总体的平均变化,这正是回归分析的意义所在。 因此,称这条线为总体回归模型。 因此,称这条线为总体回归模型。 由于它是一条直线, 由于它是一条直线,故也称为总体回归直线
计量经济学第二章

二、参数的普通最小二乘估计
Q
e
2 i
(Y
i
Yi )
2
[Y
i
( 0 1 X i )]
2
Q 对 0 , 1 求 一 阶 偏 导 令 其 为 0, 得 到 :
0 1
LOGO
LOGO
微积分 求:当x,y为多少时,F=f(x,y)最小或最大? 解:将F分别对x,y求一阶偏导,并令其等于0:
F x F y 0
例 如 : F 1 0 x 8 y 6 xy
2 3
0
如 何 求 F的 极 值 ?
由此便可解出x,y
LOGO
称为总体回归函数(PRF). 总体回归函数表明被解释变量Yi的平均状态 (总体条件期望)随解释变量Xi的变化规律。
LOGO
我们可以把总体回归函数简化为线性的形式:
E (Y X i ) 0 1 * X i
(2.1.4)
其中: 0 , 1 是未知的参数,称为回归系数。 (2.1.4)也称为线性总体回归函数。
LOGO
总体回归函数表明被解释变量Yi的平均状态 E (Y X i )随解释变量Xi的变化规律。 那么,对于某一个具体的家庭来说,它的消费支 出Yi就恰好等于给定收入水平Xi下的消费支出的平均 值(Y (X i )X i ) 吗? E E Y 所以,对于每一个具体的家庭,记
LOGO
在函数关系中,给定一个X,只有一个确定的Y与 之对应,因此X,Y都是确定性变量; 在相关关系中,给定一个X,有多个Y与之相对应, 因此当给定的X为确定性变量时,Y是一个不确定 的变量,称为随机变量。
计量经济学第二章 一元线性回归模型(1)(肖)

10
2.在经济学中,经济学家要研究个人
消费支出与个人可支配收入的依赖关系。
这种分析有助于估计边际消费倾向,就是
可支配收入每增加一元引起消费支出的平
均变化。
11
3.在企业中,我们很想知道人们对企
业产品的需求与广告费开支的关系。这种
研究有助于估计出相对于广告费支出的需
求弹性,即广告费支出每变化百分之一的
(2.3)
想想:结合表2.1的资料 ,怎样理解式(2.3)
变量Y 的原因, 给定变量X 的值也不能具
体确定变量Y的值, 而只能确定变量Y 的
统计特征,通常称变量X 与Y 之间的这种
关系为统计关系。
16
例如,企业总产出Y 与企业的资本投入
K 、劳动力投入L 之间的关系就是统计关 系。虽然资本K 和劳动力L 是影响产出Y 的两大核心要素,但是给定K 、L 的值并 不能确定产出Y 的值。因为,总产出Y 除 了受资本投入K、劳动力投入L 的影响外
在进入正式的回归理论之前,先斟酌一下变量y与变 量x可以互换的不同名称、术语。 Y 因变量 X 自变量
被解释变量 响应变量
被预测变量
解释变量 控制变量
预测变量
回归子
归回元
22
第二节
一、引例
一元线性回归模型
假定我们要研究一个局部区域的居 民消费问题,该区域共有80户家庭组成 ,将这80户家庭视为一个统计总体。
32
函数f (Xi)采取什么函数形式,是一个
需要解决的重要问题。在实际经济系统
中,我们不会得到总体的全部数据,因
而就无法据已知数据确定总体回归函数 的函数形式。同时,对总体回归函数的 形式只能据经济理论与经验去推断。
计量经济学 第二章 两变量线性回归分析.

29
二、离差分解和决定系数
离差决定的程度作为拟合度判断标准——Y的离 差被回归值 Y ˆ 或解释变量X决定的程度。 离差分解 (教材41页)。 决定系数 R 2 决定系数与残差平方和既有区别,又有联系。 [例]消费模型的决定系数。P43。 一般计量软件都直接输出 R 2
30
第五节 统计推断
本章介绍古典线性回归分析中的两变量线性回归一元线性回归包括两变量线性回归模型两变量线性回归分析思路最小二乘参数估计方法及其性质基于参数估计的检验推断和预测分析方法等
第二章 两变量线性回归分析
1
本章介绍古典线性回归分析中的两变 量线性回归(一元线性回归),包括两变 量线性回归模型,两变量线性回归分析思 路,最小二乘参数估计方法及其性质,基 于参数估计的检验推断和预测分析方法等。
19
第三节 最小二乘估计的性质
上一节介绍了用最小二乘估计两变量线性回 归模型参数的方法,但这些估计量究竟是否好, 是参数真实值的良好近似,还需要进一步研究。 本节讨论最小二乘估计的性质,可以回答上 述问题。 对参数估计性质的认识,对于理解和掌握计 量分析的方法论和方法论的发展非常重要。 性质:线性性、无偏性、最小方差性、一致 性。
585 576 615
年份
1990 1991 1992
可支配收入 Y
2181.65 2485.46 3008.97
消费性支出 C
1936 2167 2509
1984
1985 1986
834.15
1075.26 1293.24
726
992 1170
1993
1994 1995
4277.38
5868.48 7171.91
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
两个变量之间存在相关关系,还需要考虑两个变量 之间的逻辑关系—因果关系,即哪个变量依赖于哪 个变量。例如消费支出与收入之间的关系,一定是 消费支出依赖于收入,即收入是“自变量”,消费 支出是“因变量”;但是也有一些经济变量之间是 互相依赖的,如某种商品的价格与供应量之间的关 系就是互相依赖的关系。判断因果关系依据是相关 的经济理论,在统计意义上是无法判断的,所以在 进行相关分析时一般不区分因果关系。
第2章 回归与回归分析
学习目标
1、掌握线性相关系数的意义及计算方法 2、理解统计关系与确定性关系的意义 3、理解总体线性回归方程与总体回归模型的意义 4、理解随机扰动项的意义 5、理解样本回归方程与总体回归模型的意义
2.1回归的基本问题
现代意义的“回归”已经演变成建立回归方程或 模型研究一个随机变量Y对另一个变量(X)或多个 变量(X1,X2,…,Xk)的相互依存关系的统计分 析方法。 在经济领域,很多变量之间都存在着相互依存关 系。
相关分析就是研究统计关系的形式、方向和密切程 度的统计方法。为了表达问题的方便,我们约定在 本书中,用大写字母表示变量,如Y、X、X1、…、 Xk等等。
2.相关关系的种类 (1)按相关的程度可分为完全相关、不完全相关 和不相关 当两个变量之间的关系是确定性关系是,称这两种 现象间的关系为完全相关;当两个变量之间彼此互 不影响,其数量变化各自独立时,称为不相关;两 个变量之间的关系介于完全相关和不相关之间,称 为不完全相关,一般的相关关系就是指这种不完全 相关。
绘制X与Y的散点图:
6000 5500 5000 4500
Y
4000 3500 3000 2500 3000
图 2-3 收入与消费支出的散点图 4000 5000 6000 7000 8000 9000
X
由图(2-3)可以看出,消费支出的条件均值可以用 一条直线来表示: E(Y X i ) 0 1 X i (2-8) 我们称式(2-8)为总体线性回归方程,因为它是一 个一元一次方程,所以也称为总体一元线性回归方 程。 对于相同收入水平的家庭,消费支出并不一定相同。 每个家庭的具体消费支出与其条件均值会一个“偏 离”,这个偏离记为u i ,之所以加下标是因为在同 一个收入水平下,这样的偏离有多个。显然有: (2-9) ui Yi E(Y X i )
28000
24000
20000
Y
16000 12000 8000 12000 16000 20000 24000 28000 32000 36000 X
图2-1 广东省各地区城镇居民可支配收入与消费支出的关系
其中,X表示收入,Y表示消费。从图2-1可以看出, 当X增加时,Y也在增加,并且这些散点散布在某 条直线附近。于是我们可以用一条直线“近似”表 示收入(X)与消费支出(Y)的关系: (2-1) Y a bX 而其中的斜率项系数 b Y X ,即消费支出的增 量比收入的增量,其含义是边际消费倾向。
2.3 一元线性回归分析
回归分析是指在相关分析的基础上,将变量之间的 变动关系模型化,即寻找出一个能够“近似”刻画 变量间变化关系的函数关系式,并据此“精确”的 表达变量之间影响的结构、方向和程度。通过回归 分析,可以将相关变量之间不确定、不规则的数量 关系一般化、规范化,从而可以根据自变量的某一 个给定值推断出因变量的可能值(或估计值)。
图2-2 菲利普斯曲线
由图2-2,我们可以用一条双曲线“近似”表示货 币工资增长率(Y)与失业率(X)这两个变量的 规律性:
1 Y ab X
(2-2)
【例2-3】经济理论告诉我们,影响经济增长的主要 因素是消费、投资和净出口,如果用GDP作为经济 总量的代表变量,则可以用以下方程“近似”地表 示这些变量的关系: Y a bX1 cX 2 dX 3 (2-3) 其中 Y—GDP,X1—消费,X2—投资,X3—净出 口。
(2)按相关的方向可分为正相关和负相关 当一个变量的数量增加(或减少),另一个变量的 数量也随之增加(或减少)时,称为正相关;反之, 当一个变量的数量增加(或减少),而另一个变量 的数量向相反方向变动时,称为负相关。
(3)按相关的形式可分为线性相关和非线性相关 当两种相关变量之间的关系大致呈现为线性关系时, 称之为线性相关;如果两种相关变量之间,并不表 现为直线的关系,而是近似于某种曲线方程的关系, 则这种相关关系称为非线性相关。 (4)按所研究的变量多少可分为简单相关、复相关 两个变量之间的相关,称为简单相关;当所研究的 是一个变量对两个或两个以上其他变量的相关关系 时,称为复相关。
(2-4)
其中
——变量X和Y的协方差 Cov( X , Y ) ——变量X的方差 Var( X ) ——变量Y的方差
Var (Y )
可以证明, 的取值范围为-1≤ ≤1;若 为正, 则表明两变量为正相关;若 为负,则表明两变 –1,则表明两个变量完 量为负相关;如果 =1或 全相关。 根据样本数据计算的相关系数称为样本相关系数, 记为r。由于总体一般是不能全面观测的,所以相 关系数一般只能计算样本相关系数,计算公式为:
经济变量大多都是随机变量,例如消费支出、失业 率、净出口等等,正是由于这种随机性,导致经济 变量之间很难保持确定性的关系。但是,经济运行 存在的内在规律性会使经济变量之间存在着某种 “相关”,这些“相关”在实践中被反复大量的观 察,并在某种程度上被证实,于是人们描述出这些 “相关”意义,总结成相应的经济理论,这些“相 关”就是我们所理解的经济意义上的统计关系—相 关关系。
根据这些数据,说明收入对消费支出影响的规律性。
解:由经济理论可知,收入是解释变量,消费支出 是被解释变量。 从这些数据可以看出,虽然每一个收入水平对应下 的消费支出是不相同的,但平均而言当收入增加时, 消费支出也会增加。 计算每一个收入水平对应的平均消费支出,由于这 个平均值是在给定的收入条件下得到的,所以称为 条件均值,一般用符号表示,如,表示在收入水平 为4000元的条件下,消费支出是2720元。
【例2-1】边际消费倾向是凯恩斯宏观经济学的 核心概念之一。通俗的讲当人们的收入增加时, 消费支出也会增加,但消费支出增加的没有收入 增加的快,而消费支出的增加值比收入的增加就 是边际消费倾向。在这个理论中,叙述了两个经 济变量--收入与消费之间的关系,那么两者之间 存在怎样的关系呢?我们抽取2010年广东省各地 区城镇居民可支配收入与消费支出的数据(数据 见例2-1,数据来源:广东统计年鉴2011),并 绘制散点图如下:
2.3.1总体线性回归方程与回归模型 【例2-4】假设一个总体中只有100个家庭。由于这 个总体非常小,我们可以对这个总体中的所有数据 进行调查。经过调查,这100个家庭的月度收入和 消费支出数据如下:
表2-1 100个家庭收入与消费支出数据
单位:元
收入X 4000 2656 2687 2698 2698 2754 2828 4500 2931 2934 2951 2965 2997 3048 3141 消 费 支 出 Y 3157 5000 3148 3173 3202 3271 3301 3303 3320 3331 5500 3428 3564 3590 3612 3636 3651 3681 3700 6000 3722 3772 3802 3820 3823 3828 3829 3858 6500 3996 4169 4192 4238 4262 4272 4285 4292 7000 4288 4379 4417 4453 4464 4583 4752 4797 7500 4661 4694 4917 5015 5051 5056 5104 8000 4635 4857 4999 5205 5526 5690 8500 4915 5214 5523 5693
3. 简单线性相关关系的度量 简单线性相关关系是最简单也是最常见的相关形式, 一般用简单线性相关系数度量这种关系的密切程度。 简单线性相关系数简称相关系数(correlation coefficient),如果是根据总体全部数据计算的, 则称为总体相关系数,通常记为 ,计算公式为:
Cov( X , Y ) Var( X )Var(Y )
3157
3363
3374 3426 3450
3708
3720 3723 3723 3732 3787 3799
3905
3921 3969 4011 4043 4043 4063 4067 4133
4335
4381 4400 4439 4453 4551
4839
4231
Y的条件均值 2720 3031 3305 3670 3936 4305 4552 4928 5152 5336
t r n2 1 r
2
~ t (n 2)
(2-7)
其中 r—样本相关系数 n—样本容量
显著性检验的步骤如下: 1)提出假设: H0 : 0 ,H1 : 0 ; 2)由式(2-7)计算检验统计量的值; 3)确定显著性水平,根据给定的显著性水平和自 由度(n-2)查t分布表查构造拒绝域; 4)决策判断:若 t t 2 ,拒绝H0, 表明总体的两 个变量之间存在显著的线性相关关系。
r
( X X )(Y Y ) ( X X ) (Y Y )
i i 2 i i
2
(2-5)
其中
X
Y
—变量X的平均数 —变量Y的平均数
注意到式(2-5)中计算项都是离差, 设 x X X,y Y Y ,则有:
i i
i
i
r
( X X )(Y Y ) ( X X ) (Y Y )
i i 2 i i
2
x y x y
i i 2 i
2 i
