(完整版)初中数学应用题较难题及答案
初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形内点,∠∠15°.求证:△是正三角形.(初二)2.(10分)已知:如图,在四边形中,,M、N分别是、的中点,、的延长线交于E、F.求证:∠∠F.3.(10分)如图,分别以△的边、为一边,在△外作正方形和,点P是的中点,求证:点P到的距离是的一半.4.(10分)设P是平行四边形内部的一点,且∠∠.求证:∠∠.5.(10分)P为正方形内的一点,并且,2a,3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,垂直于x轴,垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线上运动时,直线上是否存在这样的点Q,使得△与△面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以、为邻边的平行四边形,求平行四边形周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形对角线上一动点(P与A、C不重合),点E在线段上,且.(1)求证:①;②⊥;(2)设,△的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线1与反比例函数(x>0)的图象交于A (1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形中,∥,,边在x轴上,过点C作⊥于点E,和反比例函数的图象交于点P,当梯形的面积为12时,请判断和的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形内点,∠∠15°.求证:△是正三角形.(初二)2.(10分)已知:如图,在四边形中,,M、N分别是、的中点,、的延长线交于E、F.求证:∠∠F.∴∥,且3.(10分)如图,分别以△的边、为一边,在△外作正方形和,点P是的中点,求证:点P到的距离是的一半.,则()4.(10分)设P是平行四边形内部的一点,且∠∠.求证:∠∠.5.(10分)P为正方形内的一点,并且,2a,3a,求正方形的边长.22,中,即正方形的边长为6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.解之得:经检验得:∴小口径水管速度为立方米7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,垂直于x轴,垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线上运动时,直线上是否存在这样的点Q,使得△与△面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以、为邻边的平行四边形,求平行四边形周长的最小值.)为双曲线)坐标代入得,所以正比例函数解析式为,,××m×(﹣所以有,)(﹣)﹣,由勾股定理得+2=28.(10分)(2008•海南)如图,P是边长为1的正方形对角线上一动点(P与A、C不重合),点E在线段上,且.(1)求证:①;②⊥;(2)设,△的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.,﹣ו×x﹣2.x2)x2﹣﹣+<时,.9.(10分)(2010•河南)如图,直线1与反比例函数(x>0)的图象交于A (1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形中,∥,,边在x轴上,过点C作⊥于点E,和反比例函数的图象交于点P,当梯形的面积为12时,请判断和的大小关系,并说明理由.()在>,即12=,即10.(10分)(2007•福州)如图,已知直线与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.代入是直线与双曲线(在双曲线××=×)))。
初中数学难题精选(附答案)

初中数学难题精选(附答案)一、数与代数1. 题目:解方程:2x 3 = 5解答思路:这是一道一元一次方程的题目。
我们需要将方程两边的项进行移项,然后求解x的值。
解答过程:2x 3 = 52x = 5 + 32x = 8x = 8 / 2x = 4答案:x = 42. 题目:计算:3^2 2^3 + 4解答思路:这是一道指数运算的题目。
我们需要先计算指数,然后进行加减运算。
解答过程:3^2 2^3 + 4= 9 8 + 4= 1 + 4= 5答案:5二、空间与图形3. 题目:一个等边三角形的边长为5cm,求它的面积。
解答思路:这是一道求等边三角形面积的题目。
我们需要使用等边三角形的面积公式:面积 = (边长^2 根号3) / 4。
解答过程:面积 = (5^2 根号3) / 4= (25 根号3) / 4= 6.25 根号3答案:6.25 根号3 平方厘米4. 题目:一个圆柱的底面半径为3cm,高为6cm,求它的体积。
解答思路:这是一道求圆柱体积的题目。
我们需要使用圆柱体积的公式:体积 = 底面积高= π 半径^2 高。
解答过程:体积= π 3^2 6= π 9 6= 54π答案:54π 立方厘米三、统计与概率5. 题目:一个班级有30名学生,其中男生20名,女生10名。
随机抽取一名学生,求抽到女生的概率。
解答思路:这是一道求概率的题目。
我们需要计算女生的人数除以总人数,得到抽到女生的概率。
解答过程:概率 = 女生人数 / 总人数= 10 / 30= 1 / 3答案:1/3初中数学难题精选(附答案)一、数与代数6. 题目:解不等式:3x 7 > 2x + 4解答思路:这是一道一元一次不等式的题目。
我们需要将不等式两边的项进行移项,然后求解x的值。
解答过程:3x 7 > 2x + 43x 2x > 4 + 7x > 11答案:x > 117. 题目:计算:4^3 / 2^2解答思路:这是一道指数运算的题目。
初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初二数学经典难题(带答案及解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)考点:正方形的性质;全等三角形的判定与性质;等边三角形的性质;等边三角形的判定。
初中数学应用题较难题及答案(共5篇)

初中数学应用题较难题及答案(共5篇)第一篇:初中数学应用题较难题及答案初中数学应用题较难题及答案问题 1:某车间原计划每周装配 36 台机床,预计若干周完成任务。
在装配了三分之一以后,改进操作技术,工效提高了一倍,结果提前一周半完成了任务.求这次任务需要装配机床总台数.问题 2:《个人所得税法》规定,公民每月工资不超过1600 元,不需要交税,超过1600 元的部分为全月应纳税所得额,但根据超过部分的多少按不同的税率交税,税表如下:全月应纳税所得额税率不超过 500 元部分 5% 500 元至 2000 元部分 10% 2000 元至5000 元部分 15% 某人 3 月份应纳税款为 117.10 元,求他当月的工资是多少?答案:问题 1:162 台问题 2:3021 元数字问题:1、一个两位数,十位上的数比个位上的数小1。
十位上的数与个位上的数的和是这个两位数的,求这个两位数。
2、一个两位数,个位上的数与十位上的数的和为7,如果把十位与个位的数对调。
那么所得的两位数比原两位数大9。
求原来的两位数。
3、一个两位数的十位上的数比个位上的数小1,如十位上的数扩大 4 倍,个位上的数减 2,那么所得的两位数比原数大 58,求原来的两位数,4、一个五位数,如果将第一位上的数移动到最后一位得到一个新的五位数(例如:此变换可以由 4321 得到 3214),新的五位数比原来的数小 11106,求原来的五位数。
5、某考生的准考证号码是一个四位数,它的千位数是一;如果把1 移到个位上去,那么所得的新数比原数的 5 倍少 49,这个考生的准考证号码是多少?年龄问题:1、姐姐 4 年前的年龄是妹妹的 2 倍,今年年龄是妹妹的 1.5 倍,求姐姐今年的年龄。
2、1992 年,妈妈 52 岁,儿子 25 岁,哪一年妈妈的年龄是儿子的4 倍.3、爸爸和女儿两人岁数加起来是91 岁,当爸爸岁数是女儿现在岁数两倍的时候,女儿岁数是爸爸现在岁数的,那么爸爸现在的年龄是多少岁,女儿现在年龄是多少岁.4、甲、乙两人共63 岁,当甲是乙现在年龄一半时,乙当时的年龄是甲现在的岁数,那么甲多少岁,乙多少岁.5、父亲与儿子的年龄和是 66 岁,父亲的年龄比儿子的年龄的3 倍少 10 岁,那么多少年前父亲的年龄是儿子的 5 倍.等积问题1、现有一条直径为12 厘米的圆柱形铅柱,若要铸造12 只直径为12 厘米的铅球,应截取多长的铅柱(损耗不计)?(球的体积公式 R2,R 为球半径)2、直径为30 厘米,高为50 厘米的圆柱形瓶里存满了饮料,现把饮料倒入底面直径为 10 厘米的圆柱形小杯中,刚好倒满 20 杯,求小杯子的高。
八年级数学经典难题(答案 解析)

初二数学经典难题一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.4.(10分)设P是平行四边形ABCD内部的一点,且∠PBA=∠PDA.求证:∠PAB=∠PCB.5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.8.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值.9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.初二数学经典难题参考答案与试题解析一、解答题(共10小题,满分100分)1.(10分)已知:如图,P是正方形ABCD内点,∠PAD=∠PDA=15°.求证:△PBC是正三角形.(初二)2.(10分)已知:如图,在四边形ABCD中,AD=BC,M、N分别是AB、CD的中点,AD、BC的延长线交MN 于E、F.求证:∠DEN=∠F.GM=BCADMG=BC3.(10分)如图,分别以△ABC的边AC、BC为一边,在△ABC外作正方形ACDE和CBFG,点P是EF的中点,求证:点P到AB的距离是AB的一半.PQ=(PQ=PQ=5.(10分)P为正方形ABCD内的一点,并且PA=a,PB=2a,PC=3a,求正方形的边长.PE=2PE==2CF=EF=CE===即正方形的边长为6.(10分)一个圆柱形容器的容积为V立方米,开始用一根小水管向容器内注水,水面高度达到容器高度一半后,改用一根口径为小水管2倍的大水管注水.向容器中注满水的全过程共用时间t分.求两根水管各自注水的速度.解之得:经检验得:∴小口径水管速度为立方米7.(10分)(2009•郴州)如图1,已知正比例函数和反比例函数的图象都经过点M(﹣2,﹣1),且P(﹣1,﹣2)为双曲线上的一点,Q为坐标平面上一动点,PA垂直于x轴,QB垂直于y轴,垂足分别是A、B.(1)写出正比例函数和反比例函数的关系式;(2)当点Q在直线MO上运动时,直线MO上是否存在这样的点Q,使得△OBQ与△OAP面积相等?如果存在,请求出点的坐标,如果不存在,请说明理由;(3)如图2,当点Q在第一象限中的双曲线上运动时,作以OP、OQ为邻边的平行四边形OPCQ,求平行四边形OPCQ周长的最小值.Y=上的一点,所以,所以正比例函数解析式为x,|OB×m|所以有,)=))﹣OP=(=28.(10分)(2008•海南)如图,P是边长为1的正方形ABCD对角线AC上一动点(P与A、C不重合),点E在线段BC上,且PE=PB.(1)求证:①PE=PD;②PE⊥PD;(2)设AP=x,△PBE的面积为y.①求出y关于x的函数关系式,并写出x的取值范围;②当x取何值时,y取得最大值,并求出这个最大值..BE PF=x﹣xx xx x=()<时,9.(10分)(2010•河南)如图,直线y=k1x+b与反比例函数(x>0)的图象交于A(1,6),B(a,3)两点.(1)求k1、k2的值.(2)直接写出时x的取值范围;(3)如图,等腰梯形OBCD中,BC∥OD,OB=CD,OD边在x轴上,过点C作CE⊥OD于点E,CE和反比例函数的图象交于点P,当梯形OBCD的面积为12时,请判断PC和PE的大小关系,并说明理由.y=的图象上,﹣=12=,即PE=CE10.(10分)(2007•福州)如图,已知直线y=x与双曲线交于A,B两点,且点A的横坐标为4.(1)求k的值;(2)若双曲线上一点C的纵坐标为8,求△AOC的面积;(3)过原点O的另一条直线l交双曲线于P,Q两点(P点在第一象限),若由点A,B,P,Q为顶点组成的四边形面积为24,求点P的坐标.xx与双曲线在双曲线××=×)))。
(word完整版)初中数学经典难题(含答案),推荐文档
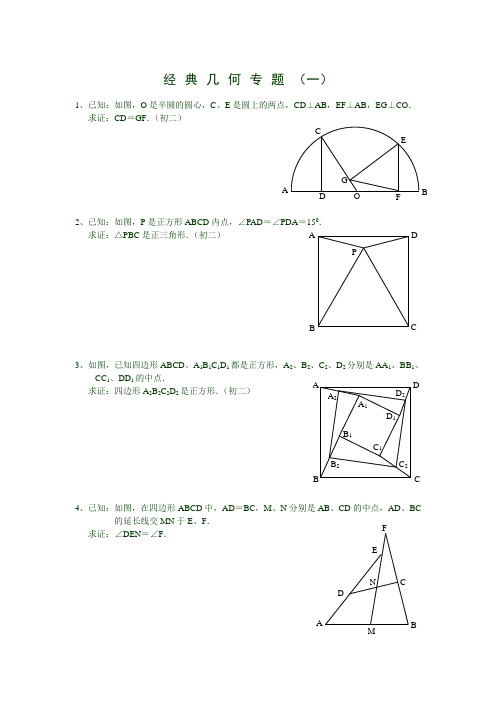
经典几何专题(一)1、已知:如图,O 是半圆的圆心,C 、E 是圆上的两点,CD ⊥AB ,EF ⊥AB ,EG ⊥CO . 求证:CD =GF .(初二)2、已知:如图,P 是正方形ABCD 内点,∠PAD =∠PDA =150. 求证:△PBC 是正三角形.(初二)3、如图,已知四边形ABCD 、A 1B 1C 1D 1都是正方形,A 2、B 2、C 2、D 2分别是AA 1、BB 1、CC 1、DD 1的中点.求证:四边形A 2B 2C 2D 2是正方形.(初二)4、已知:如图,在四边形ABCD 中,AD =BC ,M 、N 分别是AB 、CD 的中点,AD 、BC的延长线交MN 于E 、F .求证:∠DEN =∠F .A P C DB A F G CE BO D D 2 C 2B 2 A 2D 1 C 1 B 1C B DA A 1 BF经典几何专题(二)1、已知:△ABC 中,H 为垂心(各边高线的交点),O(1)求证:AH =2OM ; (2)若∠BAC =600,求证:AH =AO .(初二)2、设MN 是圆O 外一直线,过O 作OA ⊥MN 于A ,自A 及D 、E ,直线EB 及CD 分别交MN 于P 、Q . 求证:AP =AQ .(初二)3、如果上题把直线MN 由圆外平移至圆内,则由此可得以下命题:设MN 是圆O 的弦,过MN 的中点A 任作两弦BC 、DE ,设CD 、EB 分别交MN 于P 、Q . 求证:AP =AQ .(初二)4、如图,分别以△ABC 的AC 和BC 为一边,在△ABC 的外侧作正方形ACDE 和正方形CBFG ,点P 是EF 的中点.求证:点P 到边AB 的距离等于AB 的一半.宝剑锋从磨砺出,梅花香自苦寒来经典几何专题(三)1、如图,四边形ABCD 为正方形,DE ∥AC ,AE =AC ,AE 与CD 相交于F .234经典几何专题(四)1、已知:△ABC 是正三角形,P 是三角形内一点,PA =3,PB =4,PC =5.求:∠APB 的度数.(初二)2、设P 是平行四边形ABCD 内部的一点,且∠PBA =∠PDA . 求证:∠PAB =∠PCB .(初二)3、Ptolemy (托勒密)定理:设ABCD 为圆内接凸四边形,求证:AB ·CD +AD ·BC =AC ·BD . (初三)4、平行四边形ABCD 中,设E 、F 分别是BC 、AB 上的一点,AE 与CF 相交于P ,且 AE =CF .求证:∠DPA =∠DPC .(初二)宝剑锋从磨砺出,梅花香自苦寒来经典几何专题(五)1、设P是边长为1的正△ABC内任一点,l=PA+PB+PC,求证:3≤L<2.23、P4∠经典难题(一)1、2、宝剑锋从磨砺出,梅花香自苦寒来3、4、经典难题(二)1、2、宝剑锋从磨砺出,梅花香自苦寒来3、4、经典难题(三)1、2、3、4、宝剑锋从磨砺出,梅花香自苦寒来经典难题(四)1、2、3、4、证明:过D 作DQ ⊥AE ,DG ⊥CF,并连接DF 和DE ,如右图所示 则S △ADE =21S ABCD =S △DFC ∴21 AE ﹒DQ = 21 DG ﹒FC 又∵AE=FC,∴DQ=DG,∴PD 为∠APC 的角平分线,∴∠DPA=∠DPC经典难题(五)1、2、3、宝剑锋从磨砺出,梅花香自苦寒来3、4、。
(完整版)初中数学经典几何题(难)及答案分析(最新整理)

,求证:≤GF GH CDAB分别找其中点F,E.连接C F与A E并延长相交于从而得出四边形A2B2C2D2是正方形。
4.如下图连接AC并取其中点Q,连接QN和QM,所以可得∠QMF=∠F,∠QNM=∠DEN和∠QMN=∠QNM,从而得出∠DEN=∠F。
经典难题(二)1.(1)延长AD到F连BF,做OG⊥AF,又∠F=∠ACB=∠BHD,可得BH=BF,从而可得HD=DF,又AH=GF+HG=GH+HD+DF+HG=2(GH+HD)=2OM(2)连接OB,OC,既得∠BOC=1200,从而可得∠BOM=600,所以可得OB=2OM=AH=AO,得证。
经典难题(三)1.顺时针旋转△ADE,到△ABG,连接CG.由于∠ABG=∠ADE=900+450=1350从而可得B,G,D在一条直线上,可得△AGB≌△CGB。
推出AE=AG=AC=GC,可得△AGC为等边三角形。
∠AGB=300,既得∠EAC=300,从而可得∠A EC=750。
又∠EFC=∠DFA=450+300=750.可证:CE=CF。
2.连接BD作CH⊥DE,可得四边形CGDH是正方形。
由AC=CE=2GC=2CH,可得∠CEH=300,所以∠CAE=∠CEA=∠AED=150,的直线,并选一点E,使AE∥DC,BEL=(2)过P点作BC的平行线交AB,AC与点D,F。
由于∠APD>∠ATP=∠ADP,推出AD>AP ①又BP+DP>BP ②和PF+FC>PC ③又DF=AF ④由①②③④可得:最大L< 2 ;由(1)和(2)既得:≤L<2 。
2.顺时针旋转△BPC 600,可得△PBE为等边三角形。
既得PA+PB+PC=AP+PE+EF要使最小只要AP,PE,EF在一条直线上,即如下图:可得最小PA+PB+PC=AF。
4.在AB上找一点F,使∠BCF=600,连接EF,DG,既得△BGC为等边三角形,可得∠DCF=100 , ∠FCE=200 ,推出△ABE≌△ACF ,得到BE=CF ,FG=GE 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
初中数学应用题较难题及答案问题1:某车间原计划每周装配36 台机床,预计若干周完成任务。
在装配了三分之一以后,改进操作技术,工效提高了一倍,结果提前一周半完成了任务. 求这次任务需要装配机床总台数.问题2:《个人所得税法》规定,公民每月工资不超过1600 元,不需要交税,超过1600 元的部分为全月应纳税所得额,但根据超过部分的多少按不同的税率交税,税表如下:全月应纳税所得额税率不超过500 元部分5% 500 元至2000 元部分10% 2000 元至5000元部分15% 某人 3 月份应纳税款为117.10 元,求他当月的工资是多少?答案:问题1:162 台问题2:3021 元数字问题:1、一个两位数,十位上的数比个位上的数小1。
十位上的数与个位上的数的和是这个两位数的,求这个两位数。
2、一个两位数,个位上的数与十位上的数的和为7,如果把十位与个位的数对调。
那么所得的两位数比原两位数大9。
求原来的两位数。
3、一个两位数的十位上的数比个位上的数小1,如十位上的数扩大4倍,个位上的数减2,那么所得的两位数比原数大58,求原来的两位数,4、一个五位数,如果将第一位上的数移动到最后一位得到一个新的五位数(例如:此变换可以由4321 得到3214),新的五位数比原来的数小11106,求原来的五位数。
5、某考生的准考证号码是一个四位数,它的千位数是一;如果把1 移到个位上去,那么所得的新数比原数的 5 倍少49,这个考生的准考证号码是多少?年龄问题:1、姐姐 4 年前的年龄是妹妹的 2 倍,今年年龄是妹妹的1.5 倍,求姐姐今年的年龄。
2、1992 年,妈妈52 岁,儿子25 岁,哪一年妈妈的年龄是儿子的4 倍.3、爸爸和女儿两人岁数加起来是91 岁,当爸爸岁数是女儿现在岁数两倍的时候,女儿岁数是爸爸现在岁数的,那么爸爸现在的年龄是多少岁,女儿现在年龄是多少岁.4、甲、乙两人共63 岁,当甲是乙现在年龄一半时,乙当时的年龄是甲现在的岁数,那么甲多少岁,乙多少岁.5、父亲与儿子的年龄和是66 岁,父亲的年龄比儿子的年龄的3 倍少10 岁,那么多少年前父亲的年龄是儿子的5 倍.等积问题1、现有一条直径为12 厘米的圆柱形铅柱,若要铸造12 只直径为12 厘米的铅球,应截取多长的铅柱(损耗不计)?(球的体积公式R2,R 为球半径)2、直径为30 厘米,高为50 厘米的圆柱形瓶里存满了饮料,现把饮料倒入底面直径为10 厘米的圆柱形小杯中,刚好倒满20 杯,求小杯子的高。
3、用60 米长的篱笆,围成一个长方形的花圃,若长比宽的2 倍少3米,则长方形的面积是多少?4、将一个长、宽、高分别为15 厘米、12 厘米和8 厘米的长方体钢块,锻造成一个底面边长为12 厘米的正方形的长方体零件钢坯。
试问是锻造前长方体钢块的表面积大,还是锻造后的长方体零件钢坯的表面积大?请计算回答。
行程问题:(1)相遇问题:1、甲、乙两站间的路程为360 千米,一列慢车从甲站开出,每小时行48 千米,一列快车从乙站开出,每小时行72千米,已知快车先开25 分钟,两车相向而行,慢车行驶多少时间两车相遇?2、A、B 两地相距150 千米。
一辆汽车以每小时50 千米的速度从A 地出发,另一辆汽车以每小时40 千米的速度从 B 地出发,两车同时出发,相向而行,问经过几小时,两车相距30 千米?(2)追及问题:1、甲从 A 地以 6 千米/小时的速度向 B 地行走,40分钟后,乙从A 地以8 千米/小时的速度追甲,结果在甲离 B 地还有 5 千米的地方追上了甲,求A、B 两地的距离。
2、甲、乙两车都从A 地开往B 地,甲车每小时行40 千米,乙车每小时行50 千米,甲车出发半小时后,乙车出发,问乙车几小时可追上甲车?(3)航行问题:1、一轮船从甲码头顺流而下到达乙码头需要8 小时,逆流返回需要12 小时,已知水流速度是 3 千米/小时,求甲、乙两码头的距离。
2、甲乙两港相距120 千米,A、B 两船从甲乙两港相向而行6 小时相遇。
A 船顺水,B 船逆水。
相遇时 A 船比 B 船多行走49 千米,水流速度是每小时1??.5 千米,求A、B 两船的静水速度。
(4)过桥问题:1、一列火车以每分钟 1 千米的速度通过一座长400米的桥,用了半分钟,则火车本身的长度为多少米?(5)隧道问题:1、火车用26 秒的时间通过一个长256 米的隧道(即从车头进入入口到车尾离开出口),这列火车又以16 秒的时间通过了长96 米的隧道,求列车的长度。
(6)环行问题:1、甲、乙两人在环形跑道上竞走,跑道一圈长400 米,甲每分钟走100 米,乙每分钟走80 米,他们从相距40 米的A、B 两地同时出发,问出发几分钟后两人首次相遇?2、甲、乙两人环湖竞走训练,环湖一周长400 米,乙每分钟走80 米,甲的速度是乙的速度的1/4,现他们相距100 米,问几分钟后两人首次相遇?方案问题:1、某中学要添置某种教学仪器,方案1:到商店购买,每件需要8 元;方案2:学校自己制作,每件 4 元,另外需要制作工具的租用费120 元,设需要仪器x 件.(1)分别求出方案 1 和方案 2 的总费用;(2)当购制仪器多少件时,两种方案的费用相同;(3)若学校需要仪器50件,问采用哪种方案便宜?请说明理由.2、小颖的爸爸为了准备小颖3 年后读高中的费用,准备用1 万元参加教育储蓄,已知教育储蓄一年期的利率为 2.25%,三年期的利率为2.70%,现在有两种存法:①先存一年,下一年连本带息再存一年,到期后连本带息再存一年.②直接存一个三年期.请你帮着计算一下,小颖的爸爸应选择哪一种储蓄方式?3、张老师带领该校七年级“三好学生”去开展夏令营活动,甲旅行社说:“如果老师买全票一张,则学生可享受半价优惠。
”乙旅行社说:“包括老师在内按全票价的 6 折优惠。
”若全票价为240 元,当学生从数为多少人时,两家旅行社的收费一样多?4、校七年级组织学生秋游,如果租用若干辆45 座的客车,则有15 人无座位;如果租用60 座的客车,则可比45 座的客车少租 2 辆,且保证人人有座而无空位。
求:(1)七年级共有多少名学生?(2)若45 座客车的租金为每辆420 元,60 座客车的租金为每辆600 元,那么应如何安排客车的型号和数量,使得租金最少?是多少元?5、某运输公司计划用20 辆汽车装运甲、乙、丙三种水果共36 吨到外地销售,规定每辆车必须满载,每车只能装同一种水果,每种水果至少有一车。
下表所示为汽车的载重量及利润:甲乙丙每辆车载物重量(吨) 2 1 1.5 每吨水国可获利润(百元)5 7 4 问:(1)有几种运输方案?分别如何安排?(2)哪一种方案利润最大?最大利润为多少?工程问题:1、有一个水池,用两个水管注水。
如果单开甲管,2 小时30 分注满水池,如果单开乙管,5 小时注满水池. (1)如果甲、乙两管先同时注水20 分钟,然后由乙单独注水。
问还需要多少时间才能把水池注满?(2)假设在水池下面安装了排水管丙管,单开丙管 3 小时可以把一满池水放完。
如果三管同时开放,多少小时才能把一空池注满水?2、一件工作,甲单独做24 小时完成,乙单独做16 小时完成。
现在先由甲单独做4 小时,剩下的部分由甲、乙合做。
剩下的部分需要几小时完成?3、一项工程,甲单独完成需要9 天,乙单独完成需要12 天,丙单独完成需要15 天。
若甲、丙先做 3 天后,甲因故离开,由乙接替甲工作,问还需多少天能完成这项工程的?银行利率问题:1、小明的爸爸三年前为小明存了一份3000 元的教育储蓄.今年到期时取出,得本利和为3243 元.请你帮小明算一算这种储蓄的年利率.商品利润问题:1、某种商品因换季准备打折出售,如果按定价的七五折出售将赔25 元;而按定价的九折出售将赚20 元。
问这种商品的定价是多少?2、某商店为了促销G 牌空调机,2000 年元旦那天购买该机分两期付款,在购买时先付一笔款,余下部分及它的利息(年利率为 5.6%)在2001 年元旦付清.该空调机售价每台8224 元,若两次付款数相同,问每次应付款多少元?3、某工厂去年的总产值比总支出多600 万元,预计今年的总产值比去年增加30%,总支出比去年减少20%,因此今年总产值比总支出多1000 万元,问去年的总产值和总支出各是多少万元?4、某商场以每件a 元购进一种服装,如果规定以每件b 元卖出,平均每天卖出15 件,30 天共获利润22500 元.为了尽快回收资金,商场决定将每件降价20%卖出.结果平均每天比降价前多卖出10 件,这样30 天仍然可获利润22500 元,试求ab 的值(每件服装的利润=每件服装的卖出价-每件服装的进价).浓度问题:1、在含盐20﹪的盐水中加入10 千克水,变成含盐16﹪的盐水,原来的盐水是多少千克?其他问题:1、某班学生共50 人,会游泳的有27 人,会体操的有18 人,游泳、体操都不会的有15 人,那么既会游泳又会体操的有多少人?2、一台挖土机和200 名工人在水利工地挖土和运土,已知挖土机每天能挖土800 立方米,使挖出的土能每名工人每天能挖土 3 立方米或运土5立方米,如何分配挖土和运土人数,及时运走?3、国家规定个人发表文章、出版图书获得稿费的纳税计算办法是:⑴稿费高于800 元的不纳税;⑵稿费高于800 元,又不高于4000 元,应纳超过800元的那一部分稿费14%的税;⑶稿费高于4000 元,应缴纳全部稿费的11%的税。
某老师获得了2000 元稿费,他应纳税元。
4、在日历上任意圈出一竖列上的4 个数,如果这4 个数的和是54,那么这4 个数是多少呢?如果这 4 数的和是70,那么这 4 个数是多少呢?你能否找到一种最快的方法,马上说出这 4 个数是多少?问题1:小明到食堂买饭,看到A,B 两窗口前面排队的人一样多,就站在A 窗口队伍的里面,过了 2 分钟,他发现 A 窗口每分钟有 4 人买了饭离开队伍,B 窗口每分钟有 6 人买了饭离开队伍,且 B 窗口队伍后面每分钟增加5 人,此时,若小李迅速从 A 窗口转移到 B 窗口后面重新排队,将比继续在A 窗口排队提前30 秒买到饭,问开始时,有多少人排队?问题2:某学校修建了一撞 4 层的教学大楼,每层楼有 6 间教室,进出这幢大楼共有 3 道门(两道大小相同的正门和一道侧门)安全检查中,对这3 道门进行了测试:当同时开启一道正门和一道侧门时,2 分钟内可以通过400 名学生,若一道正门平均每分钟比一道侧门可多通过40 名学生(1)问平均每分钟一道正门和一道侧门各可以通过多少名学生?(2)检查中发现,紧急情况时因学生拥挤,出门的效率降低20%。
