第五章 判别分析(第1、2节 绪论、距离判别法)
合集下载
数学地质系列______5判别分析

(2)非线性判别函数
双变量: y=c1x1+c2x22 或
y=c1x12+c2x2
多变量:y=c1x1i+c2x2i+„+ckxki
i=1,为线性判别函数
i>=2,为非线性函数
一般情况下,若样品有m个变量,那么新变量y形式为:
y c1 x1 c 2 x 2
cm xm c j x j
主要思想:用统计方法将待判的未知样品与已知类 型样品进行类比,以确定待判样品应归属于哪一类。
矿产预测、地球化学分析、石油及天然气地质中都有 大量的判别类型的问题,
如,判别岩石类型、地层时代、古生物种属、判别钻井穿
过的层位的含油性、判别沉积相、判别地层的生油条件等
10
4、判别分析的具体做法
在已知类型(如A、B、C三类)中抽取样本, 然后根据每个样品的多个指标经过数学运算处理,建立每
= x - μ Σ Σ
-
1 2
-
1 2
x - μ
26
= x - μ Σ-1 x - μ
3、若变量之间是相互无关的,则协方差矩阵为对角矩阵
11 22 Σ
1 11 Σ 1 pp
另有8个待判样品。
利用SPSS软件进行计算: 由样本值得统计量F=14.4644,
对于给定的显著水平α =0.01,查表得临界值 F0.01 (4,5)
=11.4,由于
F F ,则拒绝 H0 ,
这说明A盆地和B盆地的盐泉特征有显著性的差异,
因此进行判别分析是有意义的。
下面进行判别分析:
两组间平方距离(马氏距离)为37.029
应用多元统计分析课后习题答案高惠璇第五章部分习题解答

u (2) a (2)
1 89765
(32,33)
2205
1465 4.8897 89765
u (1) u (2)
当X (1)
20 20
时,
u(
X
(1)
)
1 89765
(32,33)
20 20
4.3390
因u( X (1) ) 4.3390 u* , 判X (1) G2.
当X (1)
15 20
解 : (a) (ad )2 (ad )(ad )
aSa
aSa
a( X
(1)
X
(2) )( X aSa
(1)
X
(2) )a
def
aBa aSa
1
其中1为S 1B的最大特征值,且仅当a 1对应的
特征向量时等号成立.
又S 1B ( X (1) X (2) )( X (1) X (2) )S 1与
判X G2 , 当W ( X ) 0, 试求错判概率P(2 |1)和P(1| 2).
解 : 记a 1 ( (1) (2) ),W ( X ) ( X )a是X的
线性函数,当X
G1时,W
(X
)
~
N1
(
1
,
2 1
),
且
21
第五章 判别分析
1
E(W ( X
))
( (1)
)a
1 2
( (1)
2
PU a PU b
(1) 2
(2) 1
(1) 1
(2) 2
.
.
(b) (a)
4
第五章 判别分析
5-2 设三个总体的分布分别为: G1为N(2,0.52), G2为
判别分析

Clause) 十六.信用证生效性条款(Valid Conditions Clause) 十七.信用证特别条款(Special Conditions)
三、信用证项下单证的流转程序
① 买卖双方签订贸易合同,在合同中规定 使用信用证方式支付货款。
② 买方向当地银行提出申请,根据所签的 贸易合同填写开证申请书,落实开证保证 金,或提供其它保证,请银行(开证行) 开证。
什么是判别分析
在气象学中,由气象资料判断明天是阴天还是晴天, 是有雨还是无雨.
在市场预测中,由调查资料判断下季度(或下个月) 产品是畅销、平常或滞销.
股票持有者根据某种股票近期的变化情况判断此 种股票价格下一周是上升还是下跌.
在环境科学中,由气象条件,污染浓度等判断该地 区是属严重污染,一般污染还是无污染.
设有k个m维总体G1,G2,…,Gk,其分布特征已知(如已 知分布函数分别为F1(x),F2(x),…,Fk(x),或知道来自各 个总体的训练样本).对给定的一个新样品X,我们要判 断它来自哪个总体.
在进行判别归类时,由假设的前提,判别的依据及处 理的手法不同,可得出不同判别方法.如距离判别,Bayes 判别,Fisher判别或典型判别,逐步判别,序贯判别等.
在地质勘探中,由岩石标本的多种特征判断地层的 地质年代,是有矿还是无矿,是富矿还是贫矿.
在体育运动中,由运动员的多项运动指标来判定游 泳运动员的"苗子"是适合练蛙泳,仰泳还是自由泳等
3
第五章 判别分析
什么是判别分析
判别分析是应用性很强的一种多元统计方法, 已渗透到各个领域.但不管是哪个领域,判别分析问题 都可以这样描述:
③开证行根据开证申请书的内容,向卖方 (受益人)开出信用证,并发往(寄交) 卖方所在地银行或代理行(统称通知行)。
三、信用证项下单证的流转程序
① 买卖双方签订贸易合同,在合同中规定 使用信用证方式支付货款。
② 买方向当地银行提出申请,根据所签的 贸易合同填写开证申请书,落实开证保证 金,或提供其它保证,请银行(开证行) 开证。
什么是判别分析
在气象学中,由气象资料判断明天是阴天还是晴天, 是有雨还是无雨.
在市场预测中,由调查资料判断下季度(或下个月) 产品是畅销、平常或滞销.
股票持有者根据某种股票近期的变化情况判断此 种股票价格下一周是上升还是下跌.
在环境科学中,由气象条件,污染浓度等判断该地 区是属严重污染,一般污染还是无污染.
设有k个m维总体G1,G2,…,Gk,其分布特征已知(如已 知分布函数分别为F1(x),F2(x),…,Fk(x),或知道来自各 个总体的训练样本).对给定的一个新样品X,我们要判 断它来自哪个总体.
在进行判别归类时,由假设的前提,判别的依据及处 理的手法不同,可得出不同判别方法.如距离判别,Bayes 判别,Fisher判别或典型判别,逐步判别,序贯判别等.
在地质勘探中,由岩石标本的多种特征判断地层的 地质年代,是有矿还是无矿,是富矿还是贫矿.
在体育运动中,由运动员的多项运动指标来判定游 泳运动员的"苗子"是适合练蛙泳,仰泳还是自由泳等
3
第五章 判别分析
什么是判别分析
判别分析是应用性很强的一种多元统计方法, 已渗透到各个领域.但不管是哪个领域,判别分析问题 都可以这样描述:
③开证行根据开证申请书的内容,向卖方 (受益人)开出信用证,并发往(寄交) 卖方所在地银行或代理行(统称通知行)。
五章判别分析

测量变量:萼片与花瓣的长度,花瓣裂缝的深度, 苞的长度,花粉直径。 4.新产品的速购者与迟购者。 测量变量:教育,收入,家庭大小,过去更换品牌 的次数。 5.良好信用与不良信用风险。 测量变量:收入,年龄,信用卡数目,家庭规模。
每一组中所有样品的p维指标值 x x1, x2, , xp 构 成了该组的一个p元总体分布,我们试图主要从各组 的总体分布或其分布特征出发来判断新样品x是来自 哪一组的。
2
§5.1 引言
判别分类的例子: 1.有偿付力与无偿付力的财产责任保险公司。
测量变量:总资产,股票与债券价值,股票与债券 的市值,损失支出,盈余,签定的保费金额。 2.非溃疡胃病组(胃功能紊乱者)与控制组(“正常” 者)。 测量变量:焦虑、依赖性、罪恶感、完美主义的量 度
3
3.两种野草。
判别规则:
x x
1 2
, ,
若d 2 x,1 d 2 x, 2 若d 2 x,1 d 2 x, 2
d2 x,1d2 x,2=x μ1 Σ1 x μ1x μ2 Σ1 x μ2
=xΣ1x2xΣ1μ1 μ1Σ1μ1 xΣ1x2xΣ1μ2 μ2Σ1μ2
=2xΣ1 μ2 μ1 μ1Σ1μ1 μ2Σ1μ2
=2xΣ1 μ2 μ1μ1 μ2 Σ1 μ1 μ2
2
x
μ1
2
μ2
Σ1
μ1
μ2
2x
μ
a
2ax
μ
7
其中
μ
1 2
μ1
每一组中所有样品的p维指标值 x x1, x2, , xp 构 成了该组的一个p元总体分布,我们试图主要从各组 的总体分布或其分布特征出发来判断新样品x是来自 哪一组的。
2
§5.1 引言
判别分类的例子: 1.有偿付力与无偿付力的财产责任保险公司。
测量变量:总资产,股票与债券价值,股票与债券 的市值,损失支出,盈余,签定的保费金额。 2.非溃疡胃病组(胃功能紊乱者)与控制组(“正常” 者)。 测量变量:焦虑、依赖性、罪恶感、完美主义的量 度
3
3.两种野草。
判别规则:
x x
1 2
, ,
若d 2 x,1 d 2 x, 2 若d 2 x,1 d 2 x, 2
d2 x,1d2 x,2=x μ1 Σ1 x μ1x μ2 Σ1 x μ2
=xΣ1x2xΣ1μ1 μ1Σ1μ1 xΣ1x2xΣ1μ2 μ2Σ1μ2
=2xΣ1 μ2 μ1 μ1Σ1μ1 μ2Σ1μ2
=2xΣ1 μ2 μ1μ1 μ2 Σ1 μ1 μ2
2
x
μ1
2
μ2
Σ1
μ1
μ2
2x
μ
a
2ax
μ
7
其中
μ
1 2
μ1
判别分析

(1) 1 n1 (1) X i X (1) n1 i 1
( 2)
X ( 2)
(1) ( 2) 1 X X ( (1) ( 2 ) ) , 2 2 1 ( S1 S2 ), n1 n2 2
其中Si ( X
数学建模培训课件
判别分析
邱国新
qiugx02@
Def :判别分析是在已知研究对象分成若干类型(或 组别)并已取得各种类型的一批已知样品观测 数据,在此基础上根据某些准则建立判别式, 然后对未知类型的样品进行分类.
判别分析和聚类分析往往联合起来使用,当 总体分类不清楚时,可先用聚类分析对原来的一批 样品进行分类,然后再用判别分析建立判别式以对 新样品进行判别. 按照判别准则的不同,判别方法又分为距离判别 法,Fisher判别法,Bayes判别法和逐步判别法.
(1)当 (1) ( 2 ) 时, D 2 ( X , G2 ) D 2 ( X , G1 ) 2[ X
1 (1) 令 ( ( 2 ) ), 2
(1) ( 2 )
2
] 1 ( (1) ( 2 ) )
W ( X ) ( X ) 1 ( (1) ( 2 ) )
G2总体
X 1( 2 ) (2) X2 (2) Xn 2
( 2) X 11 ( 2) X 21 ( 2) Xn 21 ( 2) X 12 ( 2) X 22 ( 2) Xn 22 ) X 1( 2 p ( 2) X2p ( 2) Xn 2p
1
15
where
n1
( 1) ( 2) d k xk xk ,
第五章 判别分析 ppt课件

例F1如(X错),判F的2(X概),率…最…小或FK错(X判)(的均损为失p最元小分等布。函数),希望建立一 个准则,对于一个给定样品X,依据这个准则就能判断出这个
样品来自哪个总体。
2008.8 休息一下
安徽财经大学统计与应用数学学院
统计学专业主干课程——多元统计分析
5.1.2 判别分析的基本思想
……
2008.8 休息一下
安徽财经大学统计与应用数学学院
统计学专业主干课程——多元统计分析
5.1.1 引 例
这些问题有一个共同的特点,就是事先已有“类”的划分, 或事先已对某种已知样本分好了“类”。
判别分析要解决的问题就是在已知历史上用某些方法已把研 究对象分成若干类的情况下,来判定新的观测样品属于已知类 别中的哪一类。
1、按判别的组数 2、按判别函数的形式 3、按处理变量的方法 4、按判别准则
安徽财经大学统计与应用数学学院 2008.8 休息一下
返回
统计学专业主干课程——多元统计分析
5.1.3 判别分析的类型
根据资料的性质,分为定性资料的判别分析和定量资料的 判别分析。
本章的大部分内容是讨论定量资料的判别分析。
统计学专业主干课程——多元统计分析
5.2 距离判别
5.2.1 距离判别的基本思想 5.2.2 两总体距离判别 5.2.3 多总体距离判别
1、两总体距离判别 2、应用实例
安徽财经大学统计与应用数学学院 2008.8 休息一下
返回
统计学专业主干课程——多元统计分析
5.2.2 两总体距离判别
1、两总体距离判别
2008.8 休息一下
安徽财经大学统计与应用数学学院
统计学专业主干课程——多元统计分析
判别分析
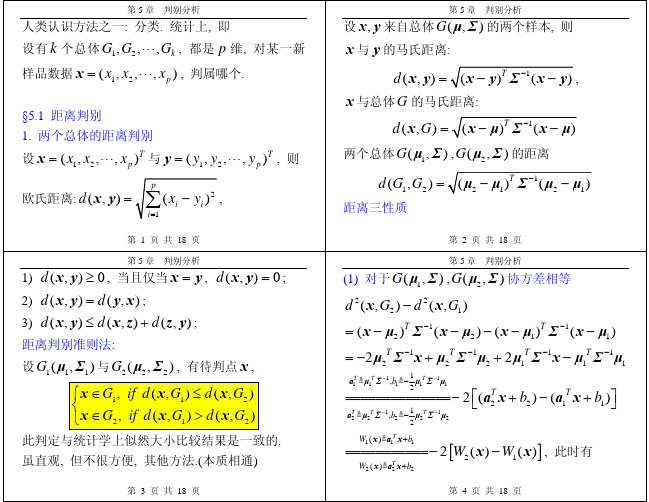
(2) 误判率的交叉确认估计法 步骤:
第 10 页 共 18 页 第 5 章 判别分析
1) 依次 G1 − { x} , 用余 n1 − 1 + n2 个,建判别准则,. 2) 判别 x , 记录正误, 直到结束, 记录误判数 n12
*
3) 对 G2 作类似步骤, 记录误判数 n21 ,
* * n12 + n21 ˆ p = n1 + n2 * c
W1 ( x ) ≥ W2 ( x )
W1 ( x )
的均值 μ1 , μ2 和协方差 S1 , S2 代总体的均值和方差.
d 2 ( x, G2 ) − d 2 ( x, G1 )
aT ( μ1 − μ2 )T Σ −1
ˆ ( n − 1) S1 + ( n2 − 1) S2 及相应的 由此得 S = Σ = 1 n1 + n2 − 2 ˆ ˆ ⎧ x ∈ G1 , if W1 ( x ) ≥ W2 ( x ) ⎪ ⎨ ˆ ˆ ⎪ x ∈ G2 , if W1 ( x ) < W2 ( x ) ⎩ ˆ ⎧ x ∈ G1 , if W ( x ) ≥ 0 ⎪ . ⎨ ˆ ( x) < 0 ⎪ x ∈ G2 , if W ⎩
此判定与统计学上似然大小比较结果是一致的. 虽直观, 但不很方便, 其他方法.(本质相通)
第 3 页 共 18 页
1 T a1 μ1T Σ −1 ,b1 − μ1T Σ −1 μ1 2
===========− 2 [W2 ( x ) − W1 ( x )] , 此时有
T W2 ( x ) a2 x + b2
G1 的 10 号, 被判为 G2 ;
G2 的 13 号和 16 号,被判为 G3 。
距离判别分析

现测得6只 蠓虫的触长,翅长数据 例1.现测得 只Apf和9只Af蠓虫的触长 翅长数据 现测得 和 只 蠓虫的触长 Apf:(1.14,1.78), (1.18,1.96), (1.20,1.86), : (1.26,2.00), (1.28,2.00), (1.30,1.96) Af:(1.24,1.72), (1.36,1.74), (1.38,1.64), : (1.38,1.82), (1.38,1.90), (1.40,1.70), (1.48,1.82),(1.54,1.82), (1.56,2.08) 若两类蠓虫协方差矩阵相等, 若两类蠓虫协方差矩阵相等,试判别以下 的三个蠓虫属于哪一类? 的三个蠓虫属于哪一类? (1.24,1.8),(1.28,1.84),( ,2.04) , ,(1.4, ,( )
如何解读计算主成分的数学表达式 我们设计算第一主成分的公式为: 我们设计算第一主成分的公式为:
Y1 = a 11 x 1 + a 12 x 2 + a 13 x 3 + a 14 x 4
的绝对值比较大, 若a11, a12 ,a14的绝对值比较大,表明第一主成 分主要提取了x1, x2 ,x4三个原始指标的信息; 三个原始指标的信息; 分主要提取了 如果此时再计算第二主成分, 如果此时再计算第二主成分,你会发现第二主 成分x 系数的绝对值就比x1, 系数的绝对 成分 3系数的绝对值就比 x2 ,x4系数的绝对 值要大, 值要大,也就是说第二主成分弥补了第一主成 分的不足. 分的不足
第四章 判别分析 判别分析利用已知类别的样本为标准, 判别分析利用已知类别的样本为标准,对未 知样本进行判类的一种统计方法。 知样本进行判类的一种统计方法。它产生于本世 30年代 近年来,在自然科学、 年代。 纪30年代。近年来,在自然科学、社会学及经济 管理学科中都有广泛的应用。 管理学科中都有广泛的应用 。 判别分析的特点 是根据已掌握的、 是根据已掌握的、历史上每个类别的若干样本的 数据信息,总结出客观事物分类的规律性, 数据信息,总结出客观事物分类的规律性,建立 判别公式和判别准则。然后, 判别公式和判别准则。然后,当遇到新的样本点 只要根据总结出来的判别公式和判别准则, 时,只要根据总结出来的判别公式和判别准则, 就能判别该样本点所属的类别。 就能判别该样本点所属的类别。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
后一种量度更合理些。
图5.1
第二节 距离判别法
更精确的说明例子,可参见教材 P.176 例子和图 5.1.
N ( , ) 更一般地,设总体G1的分布为
,设总体G2的分布为 2
,则利用统计距离,可以找出分界点 ,且不妨1设 1
N (2,,所2以2 )若令
*
1 2
(x 1)2
(x 2)2
解出
x
1
又如,在天气预报中,我们有一段较长时间关于某地区每天气象的记录资料(晴阴雨、气温、气压、湿度等),现在想建立一种 用连续五天的气象资料来预报第六天是什么天气的方法。这些问题都可以应用判别分析方法予以解决。
第一节 引言
直观上讲,判别分析是用来判别样品所属类型的一种多元统计分析方法。
这类问题可用数学语言来表达如下:设有n个样品,对每个样品测得p项指标(变量)的数据,已知每个样品 属于k个类别(或总体)G1,G2, …,Gk中的某一类,且它们的分布函数分别为F1(x),F2(x), …,Fk(x)。我们 希望利用这些数据,找出一种判别函数(或判别准则),使得这一函数具有某种最优性质,能把属于不同类别 的样本点尽可能地区别开来,并对测得同样p项指标(变量)数据的一个新样品(待判样品),能判定这个样品 归属于哪一类。
则判别规则可表示为
X X
G1 , G2 ,
如果 如果
W(X) 0 W(X) 0
这里称W (X ) 为两总体距离判别的判别函数,由于它是 X 的线
性函数,故又称为线性判别函数, α 称为判别系数。
第二节 距离判别法
在实际应用中,总体的均值和协方差矩阵一般是未知的,可
由样本均值和样本协方差矩阵分别进行估计。设
第二节 距离判别法
作为特殊情形,我们考虑:
1 X
2X
1 2
212 )
2
X
1 ( 2
1)
111
2
1 2
2X 1(2 1) (1 2 )1(1 2 )
2
X
1
2
2
1 ( 1
2
)
2(X *) 2(X *)
第二节 距离判别法
其
中
*
1 2
(1
2
)
是
两
个
总
体
均
值
的
平
均
值
,
1(1 2 ) ,记
W (X ) (X *)
X
G1,
X G2,
如果 如果
D2 (X ,G1) D2 (X ,G2) D2 (X ,G1) D2 (X ,G2 )
(*)
第二节 距离判别法
D2 ( X ,G1) D2 ( X ,G2 )
( X 1)1( X 1) ( X 2 )1( X 2 )
X
1 X
2X
1 1
111
(X
X (1) 1
,
,
X
(1) n1
来
自总体 G1 的样本,X1(2),
,
X (2) n2
是来自总体
G2的样本,1来自和2的一个无偏估计分别为
X (1)
1 n1
n1 i1
X (1) i
和
X ( 2 ) 1 n2
n2
Xi
i1
(2)
Σ 的一个联合无偏估计为
ˆ
n1
1 n2
2
(S1
S2
)
n
这里
S
(
X
( i
)
第二节 距离判别法
□ 马氏距离
设 p 维 欧 氏 空 间 R p 中 的 两 点 X ( X1, X 2, , X p ) 和
Y (Y1,Y2 , ,Yp ) ,通常我们所说的两点之间的距离,是指欧 氏距离,即 d(X, Y) 2 (X1 Y1)2 ( X p Yp )2 .
但在解决实际问题时,特别是针对多元数据的分析问题,欧氏 距离就显示出了它的一些缺陷。
定义 5.1 设 X 和 Y 是来自均值向量为 μ ,协方差为 Σ( 0) 的总体 G 中的 p 维样本,则总体 G 内两点 X 与 Y 之间的马氏距离定义为
D2 (X, Y) (X Y)Σ1(X Y)
定义点 X 到总体 G 的马氏距离为
D2 (X,G) (X μ)Σ1(X μ) 这里应该注意到,当 Σ I (单位矩阵)时,即为欧氏距离的情形。
2
21
*,
2 1
2 2
1 2
按这种距离最近的判别准则:
x x
* *
, ,
X X
G1, G2.
第二节 距离判别法
因为是单指标的问题,这时判别函数设为:
判
。
,在此例中 Y Y (因x) x
,故
* 79, x0 78 *
X 0 G2
下面给出对于m元总体的这种相对距离—即所谓的马氏距离定义
第一节 引言
■ 什么是判别分析?
在我们的日常生活和工作实践中,常常会遇到判别分析问题,即根据历史上划分类别的有关资料和某种最优准则,确定一种判别 方法,判定一个新的样品归属哪一类。
例如,在医学诊断中,一个病人肺部有阴影,医生要判断该病人患的是肺结核、肺部良性肿瘤还是肺癌?这里三种病人的集合 体可看做是三个总体,病人是来源于三个总体之一的样本。判别分析的目的是通过检测病人的一些指标(如阴影大小、边缘的光滑 度、体温等)来判定该病人应属于那个总体.
第二节 距离判别法
1、两个总体的距离判别问题
(1)
情形: 有协方差矩阵∑相等的两个总体G1和G2,其均值分别是1和 2,对于一个新的样品X,
Σ Σ Σ 要判断它来自哪1 个总体2。
一般的想法是计算新样品X到两个总体的马氏距离D2(X,G1)和D2(X,G2),并按照如下的判别规则进行
判断
这个判别规则的等价描述为:求新样品X到G1的距离与到G2的距离之差,如果其值为正,X属于G2;否则X属 于G1。
X
( )
)(
X
( i
)
X
( )
),
1, 2
i 1
第二节 距离判别法
此时,两总体距离判别的判别函数为 Wˆ ( X ) ˆ( X X *)
其中 X * 1 ( X (1) X (2) ) ,ˆ ˆ 1(X (1) X (2) ) 。这样,判别规则
2
为
X
G1
,
X G2,
如果 如果
Wˆ (X ) 0 Wˆ (X ) 0
譬 如 , 设 有 两 个 正 态 总 体 , X ~ N (1, 2 ) 和 Y ~ N (2 ,4 2 ) ,现有一个样品位于如图 5.1 所示的 A 点,距总 体 X 的中心的距离为 2 远,距总体Y 的中心的距离为 3 远, 那么, A 点处的样品到底离哪一个总体近呢?
第二节 距离判别法
若按欧氏距离来量度, A 点离总体 X 要比离总体Y “近一 些”。但是,从概率的角度看, A 点位于 1 右侧的 2 x 处,而位 于 2 左侧1.5 y 处,应该认为 A 点离总体Y “近一些”。显然,
图5.1
第二节 距离判别法
更精确的说明例子,可参见教材 P.176 例子和图 5.1.
N ( , ) 更一般地,设总体G1的分布为
,设总体G2的分布为 2
,则利用统计距离,可以找出分界点 ,且不妨1设 1
N (2,,所2以2 )若令
*
1 2
(x 1)2
(x 2)2
解出
x
1
又如,在天气预报中,我们有一段较长时间关于某地区每天气象的记录资料(晴阴雨、气温、气压、湿度等),现在想建立一种 用连续五天的气象资料来预报第六天是什么天气的方法。这些问题都可以应用判别分析方法予以解决。
第一节 引言
直观上讲,判别分析是用来判别样品所属类型的一种多元统计分析方法。
这类问题可用数学语言来表达如下:设有n个样品,对每个样品测得p项指标(变量)的数据,已知每个样品 属于k个类别(或总体)G1,G2, …,Gk中的某一类,且它们的分布函数分别为F1(x),F2(x), …,Fk(x)。我们 希望利用这些数据,找出一种判别函数(或判别准则),使得这一函数具有某种最优性质,能把属于不同类别 的样本点尽可能地区别开来,并对测得同样p项指标(变量)数据的一个新样品(待判样品),能判定这个样品 归属于哪一类。
则判别规则可表示为
X X
G1 , G2 ,
如果 如果
W(X) 0 W(X) 0
这里称W (X ) 为两总体距离判别的判别函数,由于它是 X 的线
性函数,故又称为线性判别函数, α 称为判别系数。
第二节 距离判别法
在实际应用中,总体的均值和协方差矩阵一般是未知的,可
由样本均值和样本协方差矩阵分别进行估计。设
第二节 距离判别法
作为特殊情形,我们考虑:
1 X
2X
1 2
212 )
2
X
1 ( 2
1)
111
2
1 2
2X 1(2 1) (1 2 )1(1 2 )
2
X
1
2
2
1 ( 1
2
)
2(X *) 2(X *)
第二节 距离判别法
其
中
*
1 2
(1
2
)
是
两
个
总
体
均
值
的
平
均
值
,
1(1 2 ) ,记
W (X ) (X *)
X
G1,
X G2,
如果 如果
D2 (X ,G1) D2 (X ,G2) D2 (X ,G1) D2 (X ,G2 )
(*)
第二节 距离判别法
D2 ( X ,G1) D2 ( X ,G2 )
( X 1)1( X 1) ( X 2 )1( X 2 )
X
1 X
2X
1 1
111
(X
X (1) 1
,
,
X
(1) n1
来
自总体 G1 的样本,X1(2),
,
X (2) n2
是来自总体
G2的样本,1来自和2的一个无偏估计分别为
X (1)
1 n1
n1 i1
X (1) i
和
X ( 2 ) 1 n2
n2
Xi
i1
(2)
Σ 的一个联合无偏估计为
ˆ
n1
1 n2
2
(S1
S2
)
n
这里
S
(
X
( i
)
第二节 距离判别法
□ 马氏距离
设 p 维 欧 氏 空 间 R p 中 的 两 点 X ( X1, X 2, , X p ) 和
Y (Y1,Y2 , ,Yp ) ,通常我们所说的两点之间的距离,是指欧 氏距离,即 d(X, Y) 2 (X1 Y1)2 ( X p Yp )2 .
但在解决实际问题时,特别是针对多元数据的分析问题,欧氏 距离就显示出了它的一些缺陷。
定义 5.1 设 X 和 Y 是来自均值向量为 μ ,协方差为 Σ( 0) 的总体 G 中的 p 维样本,则总体 G 内两点 X 与 Y 之间的马氏距离定义为
D2 (X, Y) (X Y)Σ1(X Y)
定义点 X 到总体 G 的马氏距离为
D2 (X,G) (X μ)Σ1(X μ) 这里应该注意到,当 Σ I (单位矩阵)时,即为欧氏距离的情形。
2
21
*,
2 1
2 2
1 2
按这种距离最近的判别准则:
x x
* *
, ,
X X
G1, G2.
第二节 距离判别法
因为是单指标的问题,这时判别函数设为:
判
。
,在此例中 Y Y (因x) x
,故
* 79, x0 78 *
X 0 G2
下面给出对于m元总体的这种相对距离—即所谓的马氏距离定义
第一节 引言
■ 什么是判别分析?
在我们的日常生活和工作实践中,常常会遇到判别分析问题,即根据历史上划分类别的有关资料和某种最优准则,确定一种判别 方法,判定一个新的样品归属哪一类。
例如,在医学诊断中,一个病人肺部有阴影,医生要判断该病人患的是肺结核、肺部良性肿瘤还是肺癌?这里三种病人的集合 体可看做是三个总体,病人是来源于三个总体之一的样本。判别分析的目的是通过检测病人的一些指标(如阴影大小、边缘的光滑 度、体温等)来判定该病人应属于那个总体.
第二节 距离判别法
1、两个总体的距离判别问题
(1)
情形: 有协方差矩阵∑相等的两个总体G1和G2,其均值分别是1和 2,对于一个新的样品X,
Σ Σ Σ 要判断它来自哪1 个总体2。
一般的想法是计算新样品X到两个总体的马氏距离D2(X,G1)和D2(X,G2),并按照如下的判别规则进行
判断
这个判别规则的等价描述为:求新样品X到G1的距离与到G2的距离之差,如果其值为正,X属于G2;否则X属 于G1。
X
( )
)(
X
( i
)
X
( )
),
1, 2
i 1
第二节 距离判别法
此时,两总体距离判别的判别函数为 Wˆ ( X ) ˆ( X X *)
其中 X * 1 ( X (1) X (2) ) ,ˆ ˆ 1(X (1) X (2) ) 。这样,判别规则
2
为
X
G1
,
X G2,
如果 如果
Wˆ (X ) 0 Wˆ (X ) 0
譬 如 , 设 有 两 个 正 态 总 体 , X ~ N (1, 2 ) 和 Y ~ N (2 ,4 2 ) ,现有一个样品位于如图 5.1 所示的 A 点,距总 体 X 的中心的距离为 2 远,距总体Y 的中心的距离为 3 远, 那么, A 点处的样品到底离哪一个总体近呢?
第二节 距离判别法
若按欧氏距离来量度, A 点离总体 X 要比离总体Y “近一 些”。但是,从概率的角度看, A 点位于 1 右侧的 2 x 处,而位 于 2 左侧1.5 y 处,应该认为 A 点离总体Y “近一些”。显然,
