最大功率定理
§4-4 最大功率传输定理.
计算可变二端电阻负载从线性电阻电路获得最大功率的步 骤是: 1.计算连接二端电阻的含源线性电阻单口网络的戴维宁等 效电路。 2.利用最大功率传输定理,确定获得最大功率的负载电阻 值RL=Ro>0. 3.计算负载电阻RL=Ro>0时获得的最大功率值。
pmax
uo2c 4Ro
例4-15 电路如图4-22(a)所示。 试求:(l) RL为何值时获得最大功率;
(2) RL获得的最大功率; (3) 10V电压源的功率传输效率。
图4-22
图4-22
解:(l)断开负载RL,求得单口网络 N1的戴维宁等效电路参 数为:
2
22
uoc 2 2 10V 5V Ro 2 2 1
如图4-22(b)所示,由此可知当RL=Ro=1时可获得最 大功率。
(2)由式(4-14)求得RL获得的最大功率
pmax
uo2c 4Ro
25 W 41
6.25W
(3)先计算10V电压源发出的功率。当RL=1时
iL
uoc Ro RL
5A 2
2.5A
i
i1
iL
2.5 2
2.5 A
3.75A
uL RLiL 2.5V p 10V 3.75A 37.5W
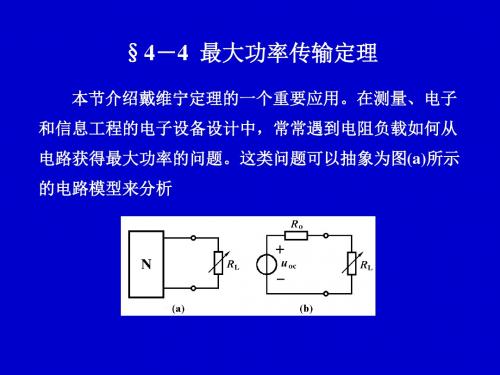
§4-4 最大功率传输定理
本节介绍戴维宁定理的一个重要应用。在测量、电子 和信息工程的电子设备设计中,常常遇到电阻负载如何从 电路获得最大功率的问题。这类问题可以抽象为图(a)所示 的电路模型来分析
网络N表示供给电阻负载能量的含源线性电阻单口网
络,它可用戴维宁等效电路来代替,如图(b)所示。电阻RL 表示获得能量的负载。此处要讨论的问题是电阻RL为何值 时,可以从单口网络获得最大功率。
最大功率定理

最大功率传输定理最大功率传输定理(maximum power transfer,theorem on)是关于使含源线性阻抗单口网络向可变电阻负载传输最大功率的条件。
定理满足时,称为最大功率匹配,此时负载电阻(分量)RL获得的最大功率为:Pmax=Uoc^2/4R0。
最大功率传输定理是关于负载与电源相匹配时,负载能获得最大功率的定理。
基本信息中文名最大功率传输定理外文名maximum power transfer学科电子技术学应用领域测量、电子与信息工程定理内容最大功率传输定理是关于负载与电源相匹配时,负载能获得最大功率的定理。
定理分为直流电路和交流电路两部分,内容如下所示。
直流电路含源线性电阻单口网络()向可变电阻负载传输最大功率的条件是:负载电阻与单口网络的输出电阻相等。
满足条件时,称为最大功率匹配,此时负载电阻RL获得的最大功率为:。
交流电路工作于正弦稳态的单口网络向一个负载供电,如果该单口网络可用戴维宁(也叫戴维南)等效电路(其中)代替,则在负载阻抗等于含源单口网络输出阻抗的共轭复数(即电阻成份相等,电抗成份只数值相等而符号相反)时,负载可以获得最大平均功率。
这种匹配称为共轭匹配,在通信和电子设备的设计中,常常要求满足共轭匹配,以便使负载得到最大功率。
计算步骤计算可变二端电阻负载从含源线性电阻电路获得最大功率的步骤是:1.计算连接二端电阻的含源线性电阻单口网络的戴维宁(也叫戴维南)等效电路。
2.利用最大功率传输定理,确定获得最大功率的负载电阻值。
3.计算负载电阻时获得的最大功率值。
使用范围满足最大功率匹配条件()时,Ro吸收功率与RL吸收功率相等,对电压源uoc而言,功率传输效率为。
对单口网络N中的独立源而言,效率可能更低。
电力系统要求尽可能提高效率,以便更充分地利用能源,不能采用功率匹配条件。
但是在测量、电子与信息工程中,常常着眼于从微弱信号中获得最大功率,而不看重效率的高低。
注意事项使用最大功率传输定理的注意事项:1、最大功率传输定理用于一端口网络的功率给定,负载电阻可调的情况;2、一端口网络等效电阻消耗的功率一般不等于端口网络内部消耗的功率,因此当负载获取最大功率时,电路的传输效率并不一定等于50%;3、计算最大功率问题结合应用戴维宁(也叫戴维南)定理或诺顿定理最方便。
最大功率传输定理

题目:最大功率传输定理专业:电气工程及其自动化班级:电气16-5姓名:柳云龙、姜乔林、袁靖昊学号:1605040508、1605040506、1605040522一.导引一个含源线性一端口电路,当所接负载不同时,一端口电路传输给负载的功率就不同,讨论负载为何值时能从电路获取最大功率,及最大功率的值是多少的问题是有工程意义的。
二.定理内容设一负载 电压型电源上,若该电源的电压保持规定值和串联电阻不变,负载 可变,则当 时,负载RL上可获得最大功率。
这就是最大功率传输定理。
三.定理证明:下面所示电路来证明最大功率传输定理。
图a中为电源的电压、R为电源的内阻、 是负载。
该电路可代表电源通过两条传输线向负载传输功率,此时,就是两根传输线的电阻。
负载 所获得的功率为上式中为电源发出的功率,=为传输效率。
将看为变量,将随变化而变化,最大功率发生在的条件下,即=求解上式得所获得的最大功率当负载电阻 时,负载可获得大功率,此种情况称为与 匹配。
最大功率问题可推广至可变化负载 从含源一端口获得功率的情况。
将含源一端口(如图b )用戴维宁等效电路来代替,其参数为与 ,当满足 时, 将获得最大功率。
我们还可以通过对关于功率P 的函数求导来得出同样的结论 2)(Leq oc L R R u R P +=对P 求导:0)()(2)( 422'=++-+=L eq L eq L L eq oc R R R R R R R u P匹配条件最大功率四.解题步骤① 求开路电压②求等效电阻③根据最大功率传输定理求解五.注意事项①最大功率传输定理用于一端口电路给定,负载电阻可调的情况。
②一端口等效电阻消耗的功率一般并不等于端口内部消耗的功率,因此当负载获取最大功率时,电路的传输效率并不一定是50%。
③计算最大功率问题结合应用戴维宁定理或诺顿定理最方便。
Welcome ToDownload !!!欢迎您的下载,资料仅供参考!④⑤。
最大功率传输定理

4A
I1
7 6
2 2
4 4
15 6
2.5A
返回 上页 下页
例3 已知:uab=0, 求电阻R
解 用替代:
uab 3I 3 0 I 1A
用结点法:
c
44
RR IRI++
aa
uC
1A
320+V3V
22
2200VV - bb -- 88 I1
a点
(1 2
1 4)ua
1 20 4
1
ua ub 8V I1 1A IR I1 1 2A
返回 上页 下页
1. 戴维宁定理
任何一个线性含源一端口网络,对外电路来说,
总可以用一个电压源和电阻的串联组合来等效置
换;此电压源的电压等于外电路断开时端口处的
开路电压uoc,而电阻等于一端口的输入电阻(或
等效电阻Req)。
i a
+
Au -b
Req +
Uoc -
ia + u
b
返回 上页 下页
例
a
10 10 +
返回 上页 下页
例 RL=2 R1=1 R2=1 us=51V,求电流 i
21A R1
+
+21V– +
us
–
R2
– us'=34V
8A R1 + 8V –
13A R2
3A R1 + 3V –
5A R2
i i '=1A
+ RL 2V
2A
–
解 采用倒推法:设 i'=1A
则 i us 即 i us i' 51 1 1.5A
8、最大功率输出定理

R0 = 0 3、 最大功率是:
u0 PLmax = 4R0
2
2 Uo
2
b
电源等效互换 但可能麻烦些
负载上 RL可以获得最大功率
3、 Pmax =
= 4Ro
12 = 3.6W 4×10
例: 电路如图,当RL 为多少时可以获得最大功 率,且为Pmax多少? 1、求戴氏等效电路 断开待求支路 5 3A
a
RL
2
4V
Uo = 6V+6V=12V Ro = 2
2、当 RL =
§3
常用电路定理(三)
内容: 最大功率输出定理
时数:1 学时
要求:说出最大功率传输定理的引出理由;
复述最大功率传输定理的内容;说出
最大功率传输定理的使用步骤;使用
最大功率传输定理分析比较简单的电
路。
重点:最大功率传输定理的应用
实际传输电路:
发送 线性有源 网络
+
动画
接收 网络 分析:
线性无源
u0
R0
-
10
+ _4V
R
b
(2) 当 R = R0 = 10 时,
有 Pmax
U = 4R0
2 0
= 1.6W
10
R
b
例:如图电路, R为何值时其上可获最大功率? 并求此最大功率。 I2 a 3I2+U 2 3 + I2 + 2 解: 断开ab
+ 4V _
2I_ 2
U 2
–
R
U0 = 2V b 3I2+U ) U = – 3I2 + 2I2 – 2×(I2 + 2 R0 = 3 2 U0 当 R = R0 = 3 时, 有 Pmax = 4R0
最大功率传输定理

第4章 电路定理与应用
小结:
பைடு நூலகம்
最大功率传输定理是戴维宁(诺顿)定理的具体
应用,若一个线性有源二端网络为负载提供最大功率,
其条件是负载电阻应与线性有源二端网络内部独立源
置零后的等效电阻相等,此时为最大功率匹配状态,
且最大功率为: 作业:
率为:
PL max
VO2C 4R
62 44
2.25(W)
第4章 电路定理与应用
+−
+−
+−
4Ω R
(a)
+
6V
− i
2Ω
+ 6V
4i
2i
4Ω
2i' 4Ω
4i'
+
− i'
2Ω
R vOC
2Ω
2Ω
(b)
−
4Ω
+
iS
i''
VOC
2Ω − 2i'R'
Req
2Ω (d)+
4Ω iS
第4章 电路定理与应用
最大功率为:
PL m ax
VOC2 4Req
第4章 电路定理与应用
此时的电路状态称最大功率匹配状态,或称为电
路达到最大功率传输。
如果有源网络用诺顿定理等效,同样可得到此时
的最大功率传输条件仍为Geq = GL,且此时的最大功 率为:
P L m ax
IS2C 4Geq
1 4
Req
I
2 SC
最大功率匹配的条件是在二端网络一定,即VOC 与Req不变的情况下推导出来。
§4-4 最大功率传输定理

计算可变二端电阻负载从线性电阻电路获得最大功率的步 骤是:
1.计算连接二端电阻的含源线性电阻单口网络的戴维宁等
效电路。 2.利用最大功率传输定理,确定获得最大功率的负载电阻 值RL=Ro>0. 3.计算负载电阻RL=Ro>0时获得的最大功率值。
例4-15 电路如图4-22(a)所示。 试求:(l) RL为何值时获得最大功率;
(2) RL获得的最大功率;
(3) 10V电压源的功率传输效率。
图4-22
图4-22
解:(l)断开负载RL,求得单口网络 N1的戴维宁等效电路参 数为:
如图4-22(b)所示,由此可知当RL=Ro=1时可获得最 大功率。
(2)由式(4-14)求得RL获得的最大功率
(3)先计算10V电压源发出的功率。当RL=1时
满足最大功率匹配条件(RL=Ro>0)时,Ro吸收功率与RL 吸收功率相等,对电压源uoc 而言,功率传输效率为
=50%。对单口网络 N中的独立源而言,效率可能更低。
电力系统要求尽可能提高效率,以便更充分地利用能源,
不能采用功率匹配条件。但是在测量、电子与信息工程中,
常常着眼于从微弱信号中获得最大功率,而不看重效率的 高低。
§4-4 最大功率传输定理
本节介绍戴维宁定理的一个重要应用。在测量、电子 和信息工程的电子设备设计中,常常遇到电阻负载如何从 电路获得最大功率的问题。这类问题可以抽象为图(a)所示
的电路模型来分析
网络 N 表示供给电阻负载能量的含源线性电阻单口网
络,它可用戴维宁等效电路来代替,如图(b)所示。电阻RL 表示获得能量的负载。此处要讨论的问题是电阻RL为何值 时,可以从单口网络获得最大功率。
整理得到
最大功率传输定理-最全资料PPT

由此式求得p为极大值或极小值的条件是
R LR o (41)2
由于
d2p dR2
L RLRo
8uRo2o3c
0
Ro0
由此可知,当Ro>0,且RL=Ro时,负载电阻RL从单口网
络获得最大功率。
最大功率传输定理:含源线性电阻单口网络(Ro>0)向
可变电阻负载RL传输最大功率的条件是:负载电阻RL与单
写出负载RL吸收功率的表达式
pRi (RRuR) 电阻RL表示获得能量的负载。
2 L
2 L oc
2 oL
整理得到
本节介绍戴维宁定理的一个重要应用。
欲求p的最大值,应满足dp/dR =0,即 解:为求uoc,按图(b)所示网孔电流的参考方向,列出网
孔方程:
万用表电阻档输出电阻测量
L
对单口网络 N中的独立源而言,效率可能更低。
为求isc,按图(c)所示网孔电流参考方向,列出网孔方程
(1 0)i1(3)isc1V 2 (3)i1(4)isc1V 2( 3)i1
整理得到
10i1 3isc 12A 4isc 12A
解得 isc=3A
为求Ro,用式(4-10)求得
Ro
uoc isc
62 3
得到单口网络的戴维宁等效电路,如图(d)所示。由式
口网络的输出电阻Ro相等。满足RL=Ro条件时,称为最大
功率匹配,此时负载电阻RL获得的最大功率为
pmax 4uR o2oc
(413)
满足最大功率匹配条件(RL=Ro>0)时,Ro吸收功率与RL
吸收功率相等,对电压源uoc 而言,功率传输效率为=50%。
对单口网络 N中的独立源而言,效率可能更低。电力系统 要求尽可能提高效率,以便更充分地利用能源,不能采用 功率匹配条件。但是在测量、电子与信息工程中,常常着 眼于从微弱信号中获得最大功率,而不看重效率的高低。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 2 RLU S 2 RLU S 有功功率 P 2 RLI P ( Ri RL ) ( X i XRi) RL ) 2 ( X i X L ) 2 (L 2
讨论正弦电流电路中负载获得最大功率Pmax的条件。 (1) ZL= RL + jXL可任意改变 (a) 先设RL不变,XL改变
最佳 匹配
2 RLU S 有功功率 P RLI ( Ri RL ) 2 ( X i X L ) 2 2
(2) 若ZL= RL + jXL只允许XL改变
获得最大功率的条件是:Xi + XL=0,即 XL =-Xi 最大功率为 Pmax
2 RLU S ( Ri RL ) 2
PL I 2 RL 6.762 2.83 129.32W
• 6.32
Байду номын сангаас9.7
有 源 网 络 负 载
最大功率传输
I
I
ZL
等效电路
Zi
+ US
Zi= Ri + jXi, ZL= RL + jXL
US I , Zi Z L
I
US ( Ri RL ) 2 ( X i X L ) 2
2 RLU S 有功功率 P RLI 2 ( Ri RL ) 2 ( X i X L ) 2
(4) 若ZL= RL+XL=|ZL| ,RL 、XL 均可改 变 ,但 XL/RL不变. (即|ZL|可变,不变)
2 RLU S P RLI 2 ( Ri RL ) 2 ( X i X L ) 2
例:电路如图所示。求(1)Z L 为何值时,它可获得最大 功率,最大功率为多少?(2)若 Z L为电阻时,求 Z L获得 的最大功率。 2 a 解:将除负载外的电路用戴维 南等效电路代替: j 4 Z 2 L 10000 A
2 RLU S 显然,当Xi + XL=0,即XL =-Xi时,P获得最大值 P ( Ri RL ) 2
(b) 再讨论RL改变时,P的最大值 当 RL= Ri 时,P获得最大值
Pmax
2 US
4Ri
综合(a)、(b),可得负载上获得最大功率的条件是:
RL= Ri XL =-Xi
ZL= Zi*
2
+ 35.36 450V Z L -
(1)由共轭匹配可得: Z L Z s* 2.83 450
PL max
2 U oc 35.362 156.16W 0 4 Rs 4 2.83 cos 45
(2)由模匹配可得:Z L 2.83
U oc 35 .36 45 0 I 6.76 67 .50 A Z s Z L 2.8345 0 2.83
(3) 若ZL= RL为纯电阻
US US , I 电路中的电流为: I 2 Z i RL ( Ri RL ) 2 X i
负载获得的功率为: P
2 RLU S
( Ri RL ) X i
2
2
dP 令 0 获得最大功率条件:RL Ri2 X i2 Z i dRL
2
0
b
j 4
U oc
U oc j 4
2 100 0 0 2 2 j4
35 .36 45 0 V
1000 A
2
4 j4 Z s 4 // j 4 2.8345 0 4 j4
2
0
2.83450
j 4
ZL
1000 A
