统计方法在大学英语四级成绩分析中的应用

合集下载

统计方法在大学英语四级成绩分析中的应用

Statistical Analysis for CET 4
Li Zaixing Hu jie Shi Xiaokai Zhao Yingwang Fan Wenfeng Huang Dan Jing Ping
（ School of Science，China University of Mining ＆ Technology， Beijing， 100083 ，China） Abstract This paper surveys the impact factors on the performance of College English Test Band Four （ CET － 4 for
x1 ， x2 ， x3 ， x4 ， x5 分别表示高考成绩及大一大二四学期的英语其中 y 表示 CET － 4 的成绩，成绩． 3． 3 回归系数的显著性检验
表3
P 值项目城市农村大一大二英语平均成绩≥70 分大一大二英语平均﹤ 70 分文科理科总的 x1 显著显著显著显著显著显著显著来自＊摘要
本文以本校 2005 级本科生为调查对象，考察影响大学生四级考试（ College English Test Band Four，简
称 CET － 4 ） CET － 4 成绩的因素．采用 Bootstrap 方法与 T 检验方法，分析得出：来自城市和农村的大学生 CET － 4 成绩存在差异；大一大二四学期英语水平不同的人 CET － 4 成绩存在显著差异；文、理科大学生 CET － 4 成绩也存在差异．进一步，我们运用多元统计中回归分析的方法建立了 CET － 4 成绩的回归模型，并利用 Logistic 模型对四级通过率进行了预测．关键词 CET － 4 成绩 Bootstrap 检验 T 检验多元回归分析 Logistic 模型

统计分析软件在大学英语教学测试效果评估中的应用——以SPSS统计分析软件为例

ＣｏｌｇｇｉｈＴｅｃｉｇＥｖｌａｉｎ／ａａｙｎｌｅＥｎｌａｈｎａｕｔｏ／ＰｎＸｉｏａｅｓ
ＡｂｓｒｔｔａｃＵｎｉｅｓｔｇｉｈｉｈｏｔｉｐｒａｔｃｒｃｌｍｖｒｉｙＥｎｌｓＳｔｅｍｓｍｏｔｎｕｒｉｕｕ
ｔｓｒｓｌｎｌｓｓｎｔｅｅｅｒｈｔｅｔｔｓｉａａｌｓｓｅｔｅｕｔａａｙｉａｄｈｒｓａｃ．ｈｓａｉｔｌｎａｙｉｃ
ｓｆｗａｅｉｈｍｐｏｔｎｘｌａｙｍｅｎ．ｏｔｒｓｔｅｉｒａｔａｕｉｒａｓｉ
求）两者之间相符合的程度。它具有双重相互关联的意思：一是测试的内容是否符合教学大纲；二是试卷的测试水平是否已达到基本要求所规定的应达到的水平。一般来说：Ｒ≥ ０７认为效度较高；．≤Ｒ０，为效度中等；＜．，为．，０５＜．认７Ｒ０认５效度不好。２２３试题的难度＿．它是主要决定试题质量和试卷合理性的关键因素。可以用没有及格的人数与总人数之比来表示。一般来说：≥ Ｐ０５．，认为试题难度较高，．≤Ｐ０５０２＜．，认为试题难度中等，ＰＯ＜．为试题难度不大。２认２２４试题的区分度．．题目对不同水平的考生加以区分的程度指标可以用区分度来表示。区分度高的试题，对考生的鉴别力就强。优生得高分，差生得低分。区分度低，就表现为优生与差生的得分差不多。优秀试题的区分度一般在０４以上，．若区分度在

成绩统计系统在大学英语测试中的应用

・83・　哈尔滨职业技术学院学报 2012年第4期 J o urna l of Ha rbi n Vo c a t i ona l & T e c h ni c a l C ol l e ge一、引言语言测试是衡量外语教学成效和提高外语教学质量的重要手段。

Bailey. KM( 1996)指出, 测试会影响学习者对教学和学习的理解和态度, 而这种理解和态度又会反过来影响学习者的学习过程和成效[1]。

这种测试对教与学的影响在教育界即被称为反拨效应(washback 或backwash )。

Hamp- Lyons( 2004)认为反拨效应这个术语用于普通教育、语言教育和语言测试中, 用来解释一种产生测试、教学和学习三者之间的相互关系和影响[2]。

大学英语学期考试和四、六级考试都涉及到听力、阅读理解、完型填空或翻译、写作等部分，针对学生的每一项成绩进行统计分析，找到学生的薄弱环节，对学生的英语水平进行把握，从而便于教师因材施教，在英语教学中有的放矢，为以后的教学积累经验，是我们进行成绩统计的目的。

从测试学的角度来说，成绩统计分析是我们英语教学中一个很重要的环节，能发现我们英语教学中的优势和不足，为下一步改良提供科学依据，因而该系统的开发和设计对提高大学英语教学的整体水平和实力奠定基础，最终达到为大学英语教学服务的目的。

大学英语是大学非英语专业学生一、二年级的基础必修课。

这门课程上课学生多，每学期参加期末考试的学生一般都在数千人。

这么多人的考试成绩需要在期末短短几天内进行统计和分析，难度可想而知。

同时，每年都有大量学生参加全国大学英语四、六级考试，他们的四、六级成绩公布后也需要尽快进行统计分析，以便及时反馈给学生，为他们改进学习提供依据。

在当前信息化时代，学生的成绩管理如果仅仅依赖于手工操作，不仅加大了管理者的工作量，而且还浪费了大量的人力、物力，并且容易造成学生成绩管理的不规范性，缺乏科学性。

大学生成绩影响因素的数据统计分析

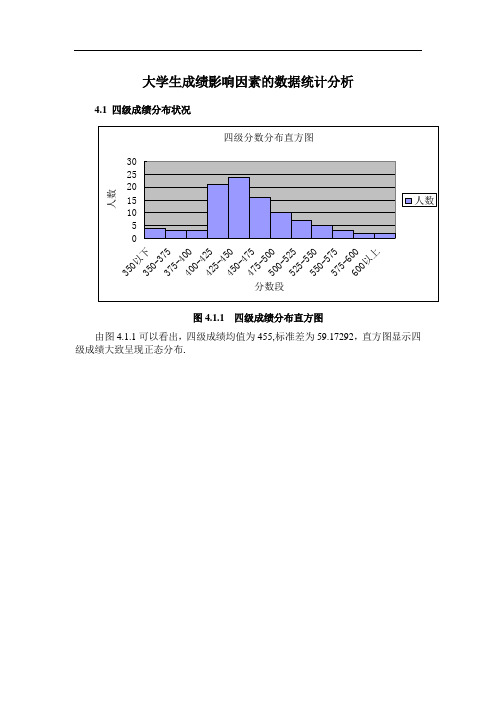
大学生成绩影响因素的数据统计分析4.1 四级成绩分布状况图4.1.1 四级成绩分布直方图由图4.1.1可以看出，四级成绩均值为455,标准差为59.17292，直方图显示四级成绩大致呈现正态分布.4.2四级成绩分布的正态性检验图4.2.1 四级成绩正态分布Q-Q图表4.2.1 单样本K-S检验统计表a. 检验分布为正态分布.b.根据数据计算得到.英语四级成绩服从正态分布.运用同样的方法可以发现均匀分布、泊松分布以及指数分布的显著性水平双尾检验结果均为0<0.05，故认为英语四级不服从这三种分布形态.综上所述，本文所采用的样本中的英语四级成绩服从正态分布.4.3 性别与四级成绩的差异分析表4.3.1性别因素与四级通过率统计图根据表4可知，男生四级通过率为63.24%，女生四级通过率为81.25%，总体显示女生四级通过率远高于男生通过率.表4.3.2男女四级成绩均值分析4.3.3ANOVA 表a我们对男生女生四级通过人数进行方差分析，由表4.3.2可知，给定显著性水α，查表得到临界值.由于所得显著性0.028<0.05,所以拒绝原假设，即有=.0平0595%的把握认为男女性别对四级通过率的影响是显著的，即性别差异对四级成绩有显著影响.表4.3.4 男女四级成绩均值差异卡方检验a. 0单元格(.0%)的期望计数少于5.最小期望计数为8.06.b.仅对2x2表计算由表4.3.4卡方检验结果显示，Pearson卡方检验为15.785，相伴概率为0.00，精确概率（Fisher's Exact Test）计算的相伴概率为0.00，均小于0.05，故说明女生的四级成绩与男生的有显著差异.综上所述，女生英语四级成绩均值与男生相比有显著差异.女生相对男生来说学习态度更端正.4.4年级与四级成绩的差异分析表4.4.1年级与四级通过率统计图从表4.4.1可以得出，大一学生的英语四级通过率为14.29%，大二学生的英语四级通过率为73.61%，大三学生的四级通过率为75.00%，大四学生的英语四级通过率为71.43%，已毕业同学的英语四级通过率为50%.总体看来，大二、大三、大四学生四级通过率基本相同.表4.4.2不同年级学生四级成绩均值分析从表4.4.2可知，在大一的学生当中，有关英语四级成绩的平均值为410分，而大二学生的英语四级成绩平均分为456分，大三学生的平均值为460分。

大学英语四级考试结果统计分析

大学英语四级考试结果统计分析01级学生02-03学年度秋季通过人数为17人，春季通过人数为27人，总人数为44人,参加考试的总人数没有记录.02级学生03-04学年度秋季通过人数为35人，春季通过人数为34人，总人数为69人, 参加考试的总人数没有记录.03级学生04-05学年度秋季通过人数为28人，春季通过人数为34人，总人数为62人，参加考试总人数为1557人，过级率为4.0%.04级学生05-06学年度秋季通过人数为49人，春季通过人数为18人，总人数为67人, 参加考试总人数为1371人，过级率为4.9%.05级学生06-07学年度秋季通过人数为93人，春季结果尚未公布，秋季参加考试总人数为1470人,过级率为6.3%.以上数据表明,我院学生四级考试通过率逐年提高,其原因分析如下:04年以前英语授课教师均为外聘教师,从04年起学院开始聘用英语专职教师,工作认真负责,主抓英语教学,使过级率有所提高. 从04年起学院组织学生参加四级考试培训,对学生进行集中辅导. 05年起学院创办了外语教学台,使学生听力水平有所提高.但从教学过程中发现如下问题:1. 职高学生的英语基础普遍差,跟不上教学进度,不爱学习,通过四级考试的学生上课专心学习,能紧密跟上教师的教学步伐.2. 影响四级考试过级率的另一主要原因是存在学生严重缺考的现象,以及学生考试中应付考试,不认真答题.3. 与其他院校相比,四级考试的不同之处在于,其他院校在考前进行全员模拟,不合格者不允许参加四级考试,参加人数少于我院,所以我院的过级率相对受到了影响.大学英语六级考试结果统计分析03级学生04-05学年度秋季通过人数为4人，春季通过人数为4人，总人数为8人，参加考试总人数为70人，过级率为11.4%.04级学生05-06学年度秋季通过人数为2人，春季通过人数为4人，总人数为6人, 参加考试总人数为73人，过级率为8.2%.05级学生06-07学年度秋季通过人数为2人，春季参加考试人数没有记录,结果尚未公布，秋季参加考试总人数为33人,过级率为6.1%.以上数据表明,我院学生六级考试的参加总人数逐年增加,通过率相对有所下降.。

英语四级成绩的影响因素分析

影响英语四级成绩的相关性分析摘要：英语四级成绩是检验大学生英语掌握水平的重要标准。

本课题通过对某高校非英语专业本科学生的大学英语四级考试成绩与考前5000常用词认知词量及高考英语成绩的相关性研究做出以下结论:1、四级统考成绩与高考英语成绩有较密切的正相关关系;2、四级成绩与考前认知词量有较密切正相关关系; 3、四级成绩同时受高考英语成绩和考前词量制约;4、若不实行分级教学,两年内通过四级统考对高考英语成绩的下限要求将必须在614分以上,对5000常用词的认知量下限要求将必须在3220以上;5、非重点院校本科生全部达四级要求有较大的难度。

并据此对目前的教学现状进行思考, 提出了相关建议。

关键词：英语四级成绩；高考英语成绩；词汇认知总量；相关性，性别。

引言:高考和四级考试作为目前国内客观性较强的两种水平考试, 有很强的信度和效度, 能够比较客观真实的反映学生从高中到大学的英语学习水平。

尽管大部分英语教师和学生都认为学生高中英语学习的基础对于其进入大学后的英语学习至关重要, 但是二者之间的关系究竟达到一个什么样的相关程度并没有得到具体的证实。

而研究两者之间的相关性程度, 对于制订大学英语教学计划, 决定教学方法以及评价教学效果都具有现实的指导意义。

问题提出：在英语教学过程中，高考英语成绩与英语专业四级成绩之间是否存在相关性一直是一个比较模糊的问题。

本次研究在揭示问题：高考英语成绩与英语专业四级成绩之间是否存在相关性？相关性如何？收集数据如下：表一高考英语成绩四级成绩的统计数据统计人数：52模型的建立与分析：将收集得到的学生高考成绩及相应的四级成绩作散点图( 图一) ,可以看到高考成绩对四级成绩是有影响的, 大致呈线性关系。

图一高考英语成绩与四级成绩的散点图用变量x表示高考英语成绩, 变量y 表示四级成绩, 利用数理统计中的回归分析可以确定x 和y的定量关系。

借助数学软件MATLAB工具箱中的命令regress求解，使用格式为：,a=data;b=a(:,3);c=a(:,1);y=a(:,2);x=[b,c];[b,brint,r,rint,stats]=regress(y,x,0.05)x 和y 的回归模型如下:y=1.4593x+ 284.2426在显著性水平 =0.05 下, 回归模型的假设检验通过, 且常数项的置信区间为[210.5480 357.9372], 一次项的置信区间为[0.7276 2.1909]四级成绩与高考成绩的拟合曲线见图二图二四级成绩与高考成绩的拟合曲线说明: 1、回归模型的假设检验: R^2 称为相关系数, R 越大, y 和x相关关系越密切, 通常, R 大于0.8( 或0.9) 才认为相关关系成立( 此模型检验中R^2=0.9653, F=0.9652)。

统计方法在学生成绩分析中的应用

1832010年・０４月・下期学　术・　理　论现代企业教育ＭＯＤＥＲＮＥＮＴＥＲＰＲＩＳＥＥＤＵＣＡＴＩＯＮ现代企业教育学生成绩不仅是反映学生学习效率和教师授课效果的一项重要指标，同时，考试成绩中蕴藏的大量信息更给教育改革提供者启示。

比如学生的以往成绩对现在或将来成绩的相关性，学生性别差异可能带来的某些学科成绩的差异等等。

本文仅以大一新生的高等数学考试成绩为例，就ＳＰＳＳ这一统计软件在学生成绩分析方面的应用做一简单探讨，以期为教学提供一定的帮助。

一、探讨背景学生的成绩蕴含的信息很多，即可以反映学生的学习效率也可以反馈出教师的教学效果。

同时，我们还可以通过统计的方法反应出试卷的难易程度、检验学生各科成绩间的相关性，男女生性别差异与学科的成绩相关性等。

本文选择某高职院校机电一体化专业四个平行班级的大一学生各科成绩作为讨论数据。

重在探索大一学生的成绩与高考成绩是否具有相关性、性别差异在文科和理工科学科成绩方面是否存在差异等。

二、成绩分析内容１．试卷成绩分析：包括平均分数、最高分、最低分、及格率、良好率、优秀率、学生人数、参加（缺考）人数、总分、标准差，图形绘制（是否成呈正态分布）等。

２．学生成绩的比较：比较班级之间和男女生之间成绩是否存在差异。

３．学生成绩的相关性：学生各科成绩的相互关系等。

三、数据文件建立１．试卷成绩的录入即可以在ＳＰＳＳ中建立数据，也可以在Ｅｘｃｅｌ中建立，然后导入ＳＰＳＳ中，设置的变量分别有班级、姓名、性别、大一各科成绩及高考成绩等。

２．定义分数段　（１）为了更清晰明白的反映不及格、及格、中、良、优的人数分布及其比率，必须把分数转换为分数段。

具体做法如下：执行Ｔｒａｎｓｆｏｒｍ→Ｒｅｃｏｄｅ　ＩｎｔｏＤｉｆｆｅｒｅｎｔ　Ｖａｒｉａｂｌｅｓ命令，弹出Ｒｅｃｏｄｅ　ＩｎｔｏＤｉｆｆｅｒｅｎｔＶａｒｉ２ａｂｌｅｓ对话框，将“高等数学”变量送入ＮｕｍｅｒｉｃＶａｒｉａｂｌｅＯｕｔｐｕｔ对话框中，在Ｏｕｔｐｕｔ　Ｖａｒｉａｂｌｅ下面的Ｎａｍｅ框中输入“分数段”，单击Ｃｈａｎｇｅ按钮；单击Ｏｌｄ　Ａｎｄ　ＮｅｗＶａｌｕｅｓ按钮，弹出ＲｅｃｏｄｅＩｎｔｏ　Ｄｉｆｆｅｒｅｎｔ　Ｖａｒｉａｂｌｅｓ　Ｏｌｄ　Ａｎｄ　Ｎｅｗ　Ｖａｌｕｅｓ对话框，选择Ｒａｎｇｅ（在此，要注意转化的变量必须是数值型的，如果是字符串型，此选项将不可用），在其下框中和Ｔｈｒｏｕｇｈ后面的框中输入相应的值，在Ｖａｌｕｅ下面的Ｖａｌｕｅ框中输入相对应的分数段，具体划分为０～５９．９９对应新值为“５０”表示不及格；６０～６９．９９对应“６０”，表示及格；７０～７９．９９对应“７０”，表示成绩为“中”；８０～８９．９９对应“８０”表示成绩“良”；９０～１００对应“９０”表示成绩为“优”。

英语四六级考试成绩统计方法

英语四六级考试成绩统计方法平均级点分：全国大学英语四、六级考试的目的是考核学生的英语能力是否达到了大学英语教学大纲规定的要求，主要是对考生个体英语能力作出评价，但同时也折射出各校、各省、市及全国对大学英语教学大纲的执行情况。

迄今为止，大学英语四、六级考试有效地促进了全国大学英语教学的改革和发展。

大学英语四、六级考试的成绩也因而常被用作对学校教学情况进行评价的依据，但利用的往往只是累计通过率这一项指标。

考试委员会认为，全国大学英语四、六级考试的成绩能够说明某个学生群体（班级、年级、学校、省、全国）的英语水平，但不能简单地用累计通过率来评价该群体的大学英语教学情况。

在说明某个学生群体的英语水平时，累计通过率只能反映出有多少学生达到了大学英语四级或六级的及格线，而不能反映这些学生在什么层次上达到了教学大纲相应级别的要求，因为60 分是及格，80 分也是及格。

为了较全面地说明某个学生群体的英语水平，考试委员会向各校提供平均级点分这一数据。

平均级点分既考虑到累计通过率，也考虑到及格学生考试成绩的高低。

平均级点分的计算公式为：G = ( S G i / N ) × 50 + 100其中：G 平均级点分G i 第i个考生的级点，其计算方法为：0 - 59.5 060 - 64.5 365 - 74.5 475 - 84.5 585 - 94.5 695 - 100 7N：该群体（学校、省、全国）在校修读大学英语课程的总人数平均级点分能更好、更准确地描写一个考生群体的实际情况。

采用平均级点分是为了鼓励各校全面提高学生运用英语的实际水平，不简单地满足于勉强及格，同时也便于有关教育行政部门对不同层次的学校实施分类指导。

平均级点分在100-400 分之间，凡平均级点分在300 分以上的学校，考生总体英语能力非常好；250-300 分考生总体英语能力很好；200-250 分，一般；150-200 分，较差；低于150 分为很差。

英语四级成绩的研究与分析

英语四级成绩的研究与分析作者：游世超吕思奇刘聪吴春霞来源：《高教学刊》2018年第03期摘要：文章运用数理统计的方法，借助统计软件SAS，对我校近三年的本科生英语成绩进行了统计和分析，研究对比了不同性别、不同生源学生的英语学业成绩和大学生英语四级成绩，并进行了差异性检验；同时对我校两种教学模式下的英语四级成绩进行了对比。

关键词：四级成绩；SAS；检验中图分类号：O213 文献标志码：A 文章编号：2096-000X（2018）03-0053-03Abstract： Guided by the mathematical statistics method and through SAS software， this study statistically analyzes English score of undergraduates from our school in recent three years. It compares English scores and CET-4 scores of undergraduate from aspects of gender and source of student. Besides the difference examination， this study also compares CET-4 score from two different teaching models.Keywords： CET4 scores； SAS； T-test大学英语四级考试是由国家教育部高等教育司主持的全国性教学考试，是测试非英语专业的大学生英语水平的重要工具，四级考试成绩在社会上被认可程度很高。

我校对学生大学英语四级考试也很重视，希望采取某些方法提高学生的英语水平。

本文利用Excel和SAS统计软件对学生的英语成绩数据进行统计和分析，从性别、生源地，教学模式等方面，研究影响大学英语四级成绩的因素。

统计分析在学生成绩评估中的应用

基于我国目前人力资源的基本状况 ,专家们提出了今后
小学及小学以下教育水平初中以下教育水平
高中和中等职业技术教育高等教育
33 % 42 % 12. 7 % 4. 7 %
教育发展的重要趋势 :大力发展高等教育 ,培养大批高层级创
新人才 ,教育发展的主攻方向应是高中阶段教育. 随着这股高教育需求之风的来临 ,相应的 ,我国的本科、
表 3 相关系数分析
相关系数
语文
数学
外语
综合科
总分 1
奖励分
总分 2
语文数学外语综合科总分 1 奖励分总分 2
1 0. 501 0. 478 0. 352 0. 713 - 0. 017 0. 691
0. 501 1
0. 399 0. 378 0. 768 0. 235 0. 779
0. 478 0. 399
0 引言
2003 年 5 月 16 日 ,教育部公布了“中国教育与人力资源表 1 2000 年我国从业人员中受教育水平
问题报告”. 报告中指出 ,我国人力资源基本现状 :整体国民素
教育水平
所占比例
质偏低 ,中高层次人才严重缺乏. 2000 年我国从业人员中受教育比例远不能满足现代经济对劳动者知识、技能的需要. 如表 1 所示.
52 5. 53 [17318 ,253132 ]
注 :1) 其中 9510 %置信度是运用正态分布的 2σ原则 ,即为标准误差的两倍 ;2) 由置信区间也可以看出 ,正态性假设在各科成绩中都不是一个很好的假定.
几个统计量的含义 : 1) 样本方差从表中该项可以看出数学和综合科的成绩相对于其它两门学科的成绩分散度显得更加厉害 ,这就表示 :在高考的总得分中 ,这两科是最容易拉开距离的科目 ,得分容易 ,失分也很容易. 因此 ,按拉开成绩距离的容易程度排序就是 :综合科 > 数学 > 外语 > 语文. 2) 偏斜度

大学生英语四级成绩影响因素的统计分析

应用概率统计课程设计大学生英语四级成绩影响因素的统计分析大学生英语四级成绩影响因素的统计分析摘要：大学生作为国家的生力军，英语能力的提高就尤为重要。

英语四级成绩是检验大学生英语掌握水平的重要标准，但目前四级通过率并不十分乐观，本文对大学生英语四级成绩影响因素进行统计分析。

本文在对相关文献研究的基础上，于2013年7月通过直接调查、网络调查等形式对全国大学生的英语四级成绩及其相关因素进行了抽样调查，并根据调查取得的数据运用了描述统计分析、统计绘图、均值比较、方差分析、相关分析等方法对影响英语四级成绩的因素进行了研究，发现：性别、英语基础、英语学习态度、英语学习方法的不同对英语四级成绩存在显著影响。

最后，根据上述数据分析结果，对改善大学生四级成绩状况提出了意见和建议。

关键词：英语四级统计方差分析卡方检验spss一引言1.1背景介绍改革开放以来，随着社会经济的发展，我国与世界各国的经济文化交流越来越多，各种语言教育应运而生。

英语作为一门世界通用语言，受到了社会上的广泛关注和重视。

大学生作为国家的生力军，英语能力的提高就尤为重要。

为此，教育部主管组织举办了全国大学英语等级考试。

全国大学英语等级考试（以下简称“四六级考试”）是教育部主管的一项全国性的教学考试，其目的是对大学生的英语能力进行客观、准确的测量，推动大学英语教学大纲的贯彻执行，为提高我国大学英语课程的教学质量服务。

四六级考试不但信度高，而且效度高，每次考试后所公布的成绩含有大量信息，成为各级教育行政部门进行决策的动态依据，也为各校根据本校实际情况采取措施提高教学质量提供了反馈信息。

但是，大学生英语四六级考试成绩受到多种因素的影响，这一现象又不断制约了英语教学质量的提高，通过对大学生英语四六级成绩影响因素的分析将有利于解决大学生英语学习中存在的问题、英语教学质量、提高大学生的综合素质。

1.2问题的提出自全国大学生英语等级考试诞生以来，围绕英语四、六级考试通过率的研究就没有中断过，例如学校之间考试成绩、四六级通过率的比较；非智力因素对英语成绩的影响；英语考试中听力、阅读、写作、完形填空及翻译等五部分成绩对英语整体成绩的影响；英语单词量、写作、口语、语法水平对英语成绩的影响等。

SPSS统计软件在考试成绩分析中的应用

一摘要考试成绩现阶段作为教学评估的一个贯用的标准,通过对考试成绩的分析能了解学生的不足, 也可以帮助教育工作者更好地进行教育设计,改进教学方法,从而达到良好的教学效果。

所以,考试成绩的数据分析相当重要。

在这篇论文中我们对同一年级的两个班级的50名学生统一进行英语考试，使用SPSS统计软件对考试成绩进行分析，得出两个班级的学生成绩的差别，进而可以了解两个班级的教学效果，使两个班级相互交流自己的教学理念，教学方式，从而达到共同发展，能满足考试成绩分析全部指标的分析计算，为教学工作起到一定的指导作用。

关键词：考试成绩T检验原理描述性统计分析二 SPSS研究的主要统计分析方法1、T检验原理T检验是用了T分布理论来推断差异发生的概率，从而比较了两个平均数的差异是否显著，T检验有单总体检验和双总体检验。

单总体T检验是检验一个样本平均数与一个已知的总体平均数的差异是否显著。

双总体T检验两个样本平均数与其各自所代表的总体差异是否显著。

2、卡方检验原理卡方检验是以卡方分布为基础的一种假设检验方法，主要用与分类变量，根据样本数据推断总体的分布是否有了显著差异，或推断两个分类变量是否相关或相互独立。

三运用SPSS软件进行数据统计对同一年级两个班级（假设为5年级）的50名学生统一进行英语考试，成绩如下先对两个班级的英语成绩进行多方面的分析,比较这两个班级的英语成绩的差异。

3.1用spss软件对考试成绩进行定义和录入在spss软件中，点击variables view标签，在Name标题下定义：学校，英语成绩，其中学校定义为school，成绩定义为Numeric，其余选项均默认。

用excel 文件做好数据，进入spss软件中，录入数据时点击File——open——data，在files of tapes中选择excel选项，以便导入数据。

3.2 对两组成绩进行分段成绩分段就是统计各个分数段的人数，将分数转化成5个等级，优秀>=90,良好（80-89），中等（70-79），及格（60-69），不及格（<60）.进行统计。

英语四级分数分配情况

英语四级分数分配情况1. 引言英语四级考试（CET-4）是中国大学生的英语能力评估考试，对学生的英语水平具有重要意义。

本文将对英语四级分数分配情况进行探讨和分析，以了解考试的整体分数分布情况、及格率以及各分数段的人数占比等关键指标。

2. 数据来源本文的数据基于近年来的英语四级考试成绩数据，并采用了以下统计方法：•综合分析历年考试原始成绩数据；•计算各分数段的人数占比；•以文本及表格形式呈现数据。

3. 分数分配情况分析3.1 总体分数分布根据数据统计，英语四级考试的总体分数分布如下：分数段人数占比600分及以上5%550-599分10%500-549分20%450-499分25%400-449分30%400分以下10%从表中可以看出，英语四级考试中，成绩在400分以下的学生占比为10%，而成绩在600分以上的学生仅占总人数的5%。

3.2 各分数段的人数占比下面将对各个分数段的人数占比进行详细分析。

•600分及以上：这个分数段的学生占总人数的5%，代表着英语水平较高的学生群体。

这部分学生通常具备较高的英语听说读写能力，能够熟练地运用英语进行学习和交流。

•550-599分：这个分数段的学生占总人数的10%，属于英语水平中上的学生。

他们的英语能力较为扎实，能够较好地理解和表达英语语言。

•500-549分：这个分数段的学生占总人数的20%，属于英语水平中等的学生。

他们的英语能力在基本应对日常交流和学习的情况下具备一定的能力。

•450-499分：这个分数段的学生占总人数的25%，属于英语水平中下的学生。

他们的英语能力相对较弱，常常会感到出现理解和表达困难的情况。

•400-449分：这个分数段的学生占总人数的30%，属于英语水平较低的学生。

他们的英语能力相对较差，对于英语语言的理解和运用存在一定的困难，需要更加努力学习。

•400分以下：这个分数段的学生占总人数的10%，为英语水平最低的学生群体。

他们对于英语语言的掌握程度较差，面对英语的理解和运用存在较大的困难，需要更加努力提升水平。

SPSS统计软件在大学英语考试成绩分析中的应用

１．３５７８２１．５１１８６
３０１５１５
Ｇｅｎｄｅｒｔｅａｃｈｅｒ１
ｔｅａｃｈｅｒ３
Ｍｅａｎ
Ｓｔｄ．Ｄｅｖｉａｔｉｏｎ
１．７２６５４
Ｎ
ｍａｌｅＴｏｔａｌ
ｍａｌｅｆｅｍａｌｅ
１１．１１．６０００２６６７
１１．４６６７６０００１１．
１．６１７４３４０４０８１．
１．１．４５４０６３５５７６
周刊 2011年第20期 ○ 考试研究
SPSS统计软件在大学英语考试成绩分析中的应用
李延波房红芳
2665 山东青岛摘要：本文借助 SPSS13.0 统计软件，从变量相关分析、双因素混合实验设计方差分析与多组配对检验等角度分析大学英语考试成绩，给出了对学生考试成绩进行分析时具体操作 SPSS13.0 软件的步骤和方法，以期直观且科学地对学生英语考试成绩进行分析。关键词： SPSS13.0 统计软件大学英语考试成绩应用
*Correlation is significant at the 0.05 level （2-tailed ）. **Correlation is significant at the 0.01 level （2-tailed ）. 表 1 数据表明，在本次考试中，所选取 30 名学生的听写成绩的标准差（standard deviation ）是 2.61868 为最大，而写作成绩的标准差是 1.35782 ，为最小。
步骤四：单击 OK 。表 1 Descriptive Statistics

大学生英语成绩的计量分析_以贵州某大学学生调查为例

2007年9月第12卷第5期西　安　邮　电　学　院　学　报JOURNAL OF XI ’AN UN IV ERSIT Y OF POST AND TEL ECOMMUN ICA TIONS Sep 12007Vol 112No 15收稿日期:2007-03-14作者简介:杨迎华(1973-),女,贵州贵阳人,贵州财经学院外语系讲师。

大学生英语成绩的计量分析———以贵州某大学学生调查为例杨迎华(贵州财经学院外语系,贵州贵阳　550004)摘要:根据教育心理学的基本原理,认为学生的英语成绩主要取决于学生的各种先天因素和大学期间的努力程度。

根据对贵州C 大学二年级学生的英语四级考试成绩及其相关因素的问卷调查所收集的数据,应用相关分析和回归分析的计量统计手法进行分析,得出以下结论:第一,英语四级考试成绩主要与包括英语高考成绩在内的各种先天因素和对英语的喜欢程度、英语学习时间的长短等后天因素正相关;第二,学生的英语学习时间的长短与对英语的喜欢程度,对教科书,英语课外读物的评价成正相关,而与对教师的英语教学没有直接关系。

关键词:四级考试;英语成绩;相关分析;回归分析中图分类号:H319 文献标识码:A 文章编号:1007-3264(2007)05-0169-04前言作为国际语言的英语在全球化进一步发展的21世纪受到了空前的重视,熟练地使用英语已经成为现代职业人士的重要标志。

作为必修课的英语以及英语四级考试,也倍受关注。

全国高校都很重视英语教学,在校大学生也把很大的精力用在英语学习和考试上,怎样提高英语学习的效率?就成为各高校和大学生所普遍关心的问题。

怎样提高英语学习的效率?很多专家都给出了很多有益的建议,在google 上用“如何提高英语成绩”搜索一下就可以得到37万多个答案;但是,这些答案大多是介绍具体的英语学习方法,而几乎没有理论和实证上的学术研究。

专家们对英语学习方法也进行了很多探索(比如陈佑林,2000),但是,到现在为止的研究仅仅局限在规范分析之上。

2013年英语专业四级考试成绩的统计分析

2013年英语专业四级考试成绩的统计分析作者：张焕新来源：《中小企业管理与科技·下旬刊》2013年第11期摘要：作为全国权威的语言测试——英语专业四级考试是大学专业英语基础教学水平的评估手段之一，它的反拨作用是不容忽视的。

本文以英语系2013年4月英语专业四级考试成绩作为研究对象，借助SPSS数据统计工具进行量化分析，总结问题，提出对策，为提高英语教学效果起到借鉴作用。

关键词：英语专业四级考试成绩统计分析 SPSS统计工具0 引言高校英语专业四级考试（以下简称TEM4）是由教育部统一组织的高等学校英语专业本科学生基础阶段的英语水平测试。

随着TEM4的信任度和权威性的逐年提高，各大高校已将TEM4的成绩作为英语教学水平的评估手段之一，更重要的是，可以通过对考试结果的分析和总结，从中发现英语语言教学和学习的规律，从而指导今后的英语教学和改革，促进教学水平及学生能力的提高。

因此，对成绩的总结和分析具有重要意义。

1 2013年TEM4考试情况（本次成绩总结和分析以2013年首次参加考试的学生成绩为主，选用2011、2012年考试成绩作为参照。

）从平均分来比较，今年全国平均分是59.17分，我院53.52分，相差5.55分；从通过率来比较，今年全国通过率是51.37%，我院为28.46%，相差22.91个百分点。

与往年相比，平均分的差距缩小了，但是通过率没有明显的提高。

为了更清晰地展现三年考试成绩的差异性，表2进行了三年考试成绩的描述性统计分析：从表2中我们可以看出，2013级学生的平均分是53.52、最大值是78分、最小值是30分、其差距是48分、标准差是9.09；2012级学生的平均分是52.45分、最大值是75分、最小值是18分、其差距是57分、标准差是8.91；2011级学生的平均分是51.86分、最大值是77分、最小值是28分、其差距是49分、标准差是8.46。

从三年学生的考试成绩的描述性统计分析表中，我们可以看出平均分是逐年提高的，最大值均在75分上下，最小值差异较大，最低达到18分，差距较大，标准差在8-9之间。

心理学统计法在英语测试的作用

心理学统计法在英语测试的作用【摘要】χ2检验法和偏度峰度检验法是经常使用的两种分布检验法。

其中偏度峰度检验法在检验正态分布中更常见。

在试卷评价系统中，对分布成绩进行正态性检验尤为重要。

本文用偏度峰度检验法对一次英语测验成绩进行了正态性检验，来检测试卷质量。

【关键字】正态性χ2检验;偏度峰度检验法;标准差;难度系数1成绩正态分布检验的意义目前，成绩测试仍是对高校学生英语学习成绩检查与评定的一种重要方法，也是教学评价的一种重要手段。

而对英语考试成绩进行正态分布检验十分重要。

主要有以下两点：一是许多重要的考试质量评价指标的计算都以成绩服从正态分布为前提，在对考试成绩及试题参数的统计过程中，使用的均值、方差等主要统计参数的估计和检验，只适用于正态分布或近似正态分布的情况，因此在使用这些统计方法前，必须进行正态性检验。

二是用于对考试成绩的解释，不同的成绩分布可以解释为试题的难度分布情况和学生的学习情况，或者在不同类型的考试中可以解释为教师的教学情况。

研究证实自然人群中个体智力分布特征为处于中等智力附近的个体数量较多，由中间向两端(智力低下和智力超强)数量逐渐减少，从形态上看是一条单峰、对称呈钟形的分布曲线，该曲线符合统计学上的正态分布。

在正常教学情况下，学生成绩受智力影响较大，应服从正态分布。

因此，英语成绩分布的正态性检验可为英语教师提高教学质量和教学行政部门改进教学管理提供可靠的科学依据。

2运用正态性检验法对大学英语测试进行评估考试成绩是考生水平的反映，同时考试成绩分布是否正态分布反映了命题质量。

根据正态分布曲线呈现的形态，可以进行考题相对难度分析。

2.1研究对象本次论文选择一份英语期末考试试卷作为样本。

期未英语考试的程序是：由英语教研室按照教学大纲对教科书的要求及学生的学习情况，并严格将学生的考试平均成绩控制在70分左右的原则，由专人负责出题。

考卷的打印、密封、分发都做到了规范化。

在整个考试过程中严格考试纪律、强化考试监督。