薛薇,《SPSS统计分析方法及应用》第六章 方差分析
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
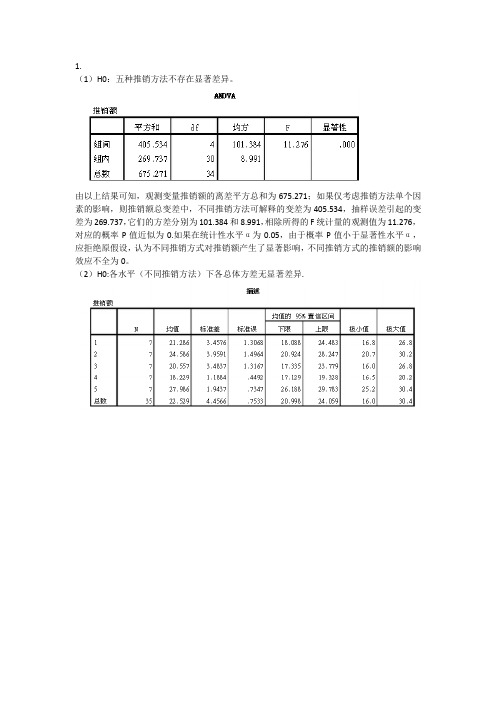
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.016.817.921.223.926.822.4第二组24.921.322.630.229.922.520.7第三组16.020.117.320.922.026.820.8第四组17.518.220.217.719.118.416.5第五组25.226.226.929.330.429.728.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析比较均值单因素ANOVA因变量:销售额;因子:组别确定。
ANOVA销售额平方和df均方F显著性组之间405.5344101.38411.276.000组内269.737308.991总计675.27134概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项均值图;事后多重比较LSD多重比较因变量:销售额LSD(L)95%置信区间平均差(I)组别(J)组别(I-J)标准错误显著性下限值上限第一组第二组-3.30000 *1.60279.048-6.5733-.0267第三组.728571.60279.653-2.54484.0019第四组3.057141.60279.066-.21626.3305第五组-6.70000 *1.60279.000-9.9733-3.4267*1.60279.048.02676.5733第二组第一组3.30000第三组4.02857 *1.60279.018.75527.3019*1.60279.0003.08389.6305第四组6.35714*第五组-3.400001.60279.042-6.6733-.1267第三组第一组-.728571.60279.653-4.00192.5448第二组-4.02857 *1.60279.018-7.3019-.7552第四组2.328571.60279.157-.94485.6019第五组-7.42857 *1.60279.000-10.7019-4.1552第四组第一组-3.057141.60279.066-6.3305.2162第二组-6.35714 *1.60279.000-9.6305-3.0838第三组-2.328571.60279.157-5.6019.9448第五组-9.75714 *1.60279.000-13.0305-6.4838*1.60279.0003.42679.9733第五组第一组6.70000*1.60279.042.12676.6733第二组3.40000*1.60279.0004.155210.7019第三组7.42857*1.60279.0006.483813.0305第四组9.75714*.均值差的显著性水平为0.05。
统计分析与SPSS的应用薛薇第四版的第六章课后习题:第一题
1.
(1)H0:五种推销方法不存在显著差异。
由以上结果可知,观测变量推销额的离差平方总和为675.271;如果仅考虑推销方法单个因素的影响,则推销额总变差中,不同推销方法可解释的变差为405.534,抽样误差引起的变差为269.737,它们的方差分别为101.384和8.991,相除所得的F统计量的观测值为11.276,对应的概率P值近似为0.如果在统计性水平α为0.05,由于概率P值小于显著性水平α,应拒绝原假设,认为不同推销方式对推销额产生了显著影响,不同推销方式的推销额的影响效应不全为0。
(2)H0:各水平(不同推销方法)下各总体方差无显著差异.
上表是推销方法对推销额的单因素方差分析结果。
可以看到:不同推销方法下推销额的方差齐性检验值为2.048,概率P-值为0.113大于显著性水平0.05,不应拒绝原假设,认为不同推销方法下推销额的总体方差无显著差异,满足方差分析的前提要求。
H0:不同推销方式没有对推销额产生显著影响,即:不同水平下控制因素的影响不显著。
由第一题可得:
在此之后检验:
在LSD方法中,第一组和第三组的效果没有明显的差异(概率P值为0.653),第一组和第四组的效果没有明显的差异(概率P值为0.066);与第二组和第五组有明显的差异(概率P 值分别为0.048,接近0)。
统计分析与SPSS的应用(第五版)课后练习答案(第6章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:1)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析→比较均值→单因素ANOV A→因变量:销售额;因子:组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间405.534 4 101.384 11.276 .000组内269.737 30 8.991总计675.271 34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
可知,1和2、1和5、2和3,2和4,2和5,3和5,4和5有显著差异。
2、从两个总体中分别抽取n 1 =7 和和n 2 =6 的两个独立随机样本,经计算得到下面的方差分析表。
请补充表中单元格的两个独立随机样本,经计算得到下面的方差分析表。
请补充表中单元格“A”和单元格“B”内的计算结果。
答:已知组内均方=组内偏差平方和/自由度,所以A=26.4/11=2.4F 统计量=组间均方/组内均方所以B=7.5/2.4=3.1253、为研究某种降血压药的适用特点,在五类具有不同临床特征的高血压患者中随机挑选了若干志愿者进行对比试验,并获得了服用该降压药后的血压变化数据。
现对该数据进行单因素方差分析,所得部分分析结果如下表所示。
1)请根据表格数据说明以上分析是否满足方差分析的前提要求,为什么?2)请填写表中空缺部分的数据结果,并说明该降压药对不同组患者的降压效果是否存在显著差异。
3)如果该降压药对不同组患者的降压效果存在显著差异,那么该降压药更适合哪组患者?(1)因F检验的概率P值小于显著性水平(0.05),拒绝原假设,方差不齐,不满足方差分析的前提假设。
SPSS人大薛微 第三版 课后习题

SPSS人大薛微第三版课后习题spss人大薛微第三版课后习题五点二independentsamplestestlevene's TestForeQuality of Variances T-TestForeQuality of Means?ò等变差被统计为等变差未被统计257.985.000f9.6409.815sig.381345.536t.000.000df.41978.41978sig.(2-tailed).04354.04277meandifference.33416.33566std.erdifferen.5054.5039第六章p179-1811组内组间方差分析销售数据总计405 534269.737675.271DF43034平均平方101。
3848.991f11。
276sig。
根据单因素方差分析结果,观察变量销售量总偏差的平方和为675.271,不同销售方法可解释的变化为405.534,抽样误差引起的变化为269.727。
它们的方差分别为101.384和8.991。
F统计量的观测值为11.276,相应的概率p值为0。
如果显著性水平为0.05,因为P小于0.05,则应拒绝原始假设,即不同营销方法对销售的影响为0.05*.themeandifferenceissignificantatthe0.05level.均值对比图如上图所示。
由lsd 方法得出的多重检验结果可知,如果显著性水平为0.05,则第一组和第三组没有显著差异,第三组和第四组差异不显著,但其他组两两之间差异非常显著。
2.(1)根据方差齐性检验表中的数据,如果显著性水平为0.05,则应拒绝原始假设,因为概率p值小于显著性水平。
认为不同类型高血压患者的血压差总体方差存在显著差异,不符合方差分析的前提要求。
(2)根据单因素方差分析结果,如果显著性水平为0.05,则应拒绝原始假设,因为概率p值为0,即抗高血压药物对不同组患者的降压效果存在显著差异。
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)
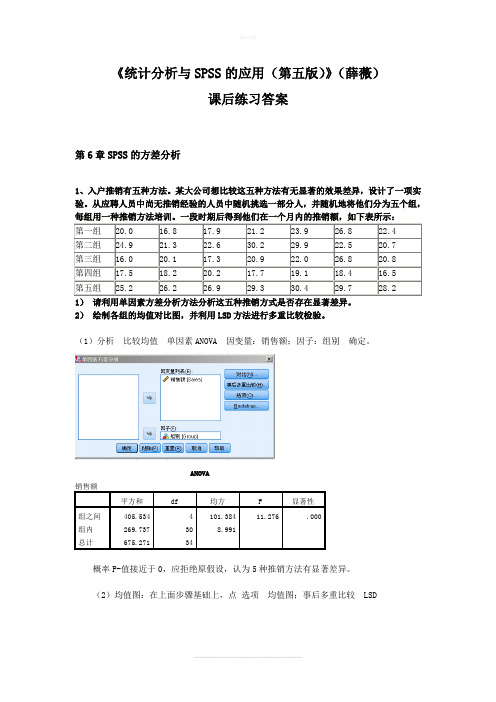
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.016.817.921.223.926.822.4第二组24.921.322.630.229.922.520.7第三组16.020.117.320.922.026.820.8第四组17.518.220.217.719.118.416.5第五组25.226.226.929.330.429.728.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析比较均值单因素ANOVA因变量:销售额;因子:组别确定。
ANOVA销售额平方和df均方F显著性组之间405.5344101.38411.276.000组内269.737308.991总计675.27134概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项均值图;事后多重比较LSD多重比较因变量: 销售额LSD(L)(I) 组别(J) 组别平均差(I-J)标准错误显著性95% 置信区间下限值上限第一组第二组-3.30000* 1.60279.048-6.5733-.0267第三组.72857 1.60279.653-2.5448 4.0019第四组 3.05714 1.60279.066-.2162 6.3305第五组-6.70000* 1.60279.000-9.9733-3.4267第二组第一组 3.30000* 1.60279.048.0267 6.5733第三组 4.02857* 1.60279.018.75527.3019第四组 6.35714* 1.60279.000 3.08389.6305第五组-3.40000* 1.60279.042-6.6733-.1267第三组第一组-.72857 1.60279.653-4.0019 2.5448第二组-4.02857* 1.60279.018-7.3019-.7552第四组 2.32857 1.60279.157-.9448 5.6019第五组-7.42857* 1.60279.000-10.7019-4.1552第四组第一组-3.05714 1.60279.066-6.3305.2162第二组-6.35714* 1.60279.000-9.6305-3.0838第三组-2.32857 1.60279.157-5.6019.9448第五组-9.75714* 1.60279.000-13.0305-6.4838第五组第一组 6.70000* 1.60279.000 3.42679.9733第二组 3.40000* 1.60279.042.1267 6.6733第三组7.42857* 1.60279.000 4.155210.7019第四组9.75714* 1.60279.000 6.483813.0305*. 均值差的显著性水平为 0.05。
(完整word版)《统计分析与SPSS的应用(第五版)》课后练习答案(第6章)

《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,每组用一种推销方法培训。
一段时期后得到他们在一个月内的推销额,如下表所示:第一组20.0 16.8 17.9 21.2 23.9 26.8 22.4 第二组24.9 21.3 22.6 30.2 29.9 22.5 20.7 第三组16.0 20.1 17.3 20.9 22.0 26.8 20.8 第四组17.5 18.2 20.2 17.7 19.1 18.4 16.5 第五组25.2 26.2 26.9 29.3 30.4 29.7 28.2 1)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析比较均值单因素ANOV A 因变量:销售额;因子:组别确定。
ANOVA销售额平方和df 均方 F 显著性组之间405.534 4 101.384 11.276 .000组内269.737 30 8.991总计675.271 34概率P-值接近于0,应拒绝原假设,认为 5 种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项均值图;事后多重比较LSD多重比较因变量: 销售额LSD(L)95% 置信区间平均差(I) 组别(J) 组别(I-J) 标准错误显著性下限值上限第一组第二组-3.30000 * 1.60279 .048 -6.5733 -.0267 第三组.72857 1.60279 .653 -2.5448 4.0019第四组 3.05714 1.60279 .066 -.2162 6.3305第五组-6.70000 * 1.60279 .000 -9.9733 -3.4267 * 1.60279 .048 .0267 6.5733 第二组第一组 3.30000 第三组 4.02857 * 1.60279 .018 .7552 7.3019* 1.60279 .000 3.0838 9.6305 第四组 6.35714*第五组-3.40000 1.60279 .042 -6.6733 -.1267 第三组第一组-.72857 1.60279 .653 -4.0019 2.5448 第二组-4.02857 * 1.60279 .018 -7.3019 -.7552第四组 2.32857 1.60279 .157 -.9448 5.6019第五组-7.42857 * 1.60279 .000 -10.7019 -4.1552 第四组第一组-3.05714 1.60279 .066 -6.3305 .2162第二组-6.35714 * 1.60279 .000 -9.6305 -3.0838第三组-2.32857 1.60279 .157 -5.6019 .9448第五组-9.75714 * 1.60279 .000 -13.0305 -6.4838* 1.60279 .000 3.4267 9.9733 第五组第一组 6.70000 * 1.60279 .042 .1267 6.6733 第二组 3.40000* 1.60279 .000 4.1552 10.7019 第三组7.42857* 1.60279 .000 6.4838 13.0305 第四组9.75714*. 均值差的显著性水平为0.05 。
SPSS_第6章 方差分析
-12.3756
15.7090
-31.0423
-2.9577
-15.7090
12.3756
-32.7090
-4.6244
2.9577
31.0423
4.6244
32.7090
40
结果2
英语
Subset for alpha = .05
Student-Newman-Keul sa
g rou p 2 1 3 Si g.
Std. Deviation 13.70280 12.42176 6.96898 13.79175
Std. Error 5.59414 5.07116 2.84507 3.25075
95% Confidence Interval for M ea n
Lower Bound Upper Bound
58.7865
75 70
74
80 72
72
77 66
68
68 72
71
75 70
71
75 70
Xt =72
4
从上表可知,三种不同实验教材的教学效果不完全 一致,表现在三个不同实验处理组的平均数之间存 在差异;同时,同一实验组内部的5名样本的反应变 量也存在差异。
5
我们可以将三个实验组的所有15名样本分数的差异 分为两部分:实验组间的差异(称为组间差异)和 实验组内的差异(称为组内差异)。
18.66667* 6.58815
*. The mean difference is significant at the .05 level.
Si g. .804 .021 .804 .013 .021 .013
95% Confidence Interval
《统计分析与SPSS的应用(第五版)》课后练习答案(第6章).doc
《统计分析与SPSS的应用(第五版)》课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,第一组20.0 16.8 17.9 21.2 23.9 26.8 22.4第二组24.9 21.3 22.6 30.2 29.9 22.5 20.7第三组16.0 20.1 17.3 20.9 22.0 26.8 20.8第四组17.5 18.2 20.2 17.7 19.1 18.4 16.5第五组25.2 26.2 26.9 29.3 30.4 29.7 28.21)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析→比较均值→单因素ANOV A→因变量:销售额;因子:组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间405.534 4 101.384 11.276 .000组内269.737 30 8.991总计675.271 34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项→均值图;事后多重比较→LSD多重比较因变量: 销售额LSD(L)(I) 组别(J) 组别平均差(I-J) 标准错误显著性95% 置信区间下限值上限第一组第二组-3.30000* 1.60279 .048 -6.5733 -.0267 第三组.72857 1.60279 .653 -2.5448 4.0019第四组 3.05714 1.60279 .066 -.2162 6.3305第五组-6.70000* 1.60279 .000 -9.9733 -3.4267 第二组第一组 3.30000* 1.60279 .048 .0267 6.5733 第三组 4.02857* 1.60279 .018 .7552 7.3019第四组 6.35714* 1.60279 .000 3.0838 9.6305第五组-3.40000* 1.60279 .042 -6.6733 -.1267 第三组第一组-.72857 1.60279 .653 -4.0019 2.5448 第二组-4.02857* 1.60279 .018 -7.3019 -.7552第四组 2.32857 1.60279 .157 -.9448 5.6019第五组-7.42857* 1.60279 .000 -10.7019 -4.1552 第四组第一组-3.05714 1.60279 .066 -6.3305 .2162第二组-6.35714* 1.60279 .000 -9.6305 -3.0838第三组-2.32857 1.60279 .157 -5.6019 .9448第五组-9.75714* 1.60279 .000 -13.0305 -6.4838第五组第一组 6.70000* 1.60279 .000 3.4267 9.9733 第二组 3.40000* 1.60279 .042 .1267 6.6733第三组7.42857* 1.60279 .000 4.1552 10.7019第四组9.75714* 1.60279 .000 6.4838 13.0305*. 均值差的显著性水平为 0.05。
SPSS基础学习方差分析—单因素分析
SPSS基础学习⽅差分析—单因素分析为什么要进⾏⽅差分析?单样本、两样本t检验其最终⽬的都是分析两组数据间是否存在显著性差异,但如果要分析多组数据间是否存在显著性差异就很困难,因此⽤⽅差分析解决这个问题;举例:t检验可以分析⼀个班男⼥的⼊学成绩差异;⽽⽅差分析可以分析⼀个班来⾃各省市地区同学的⼊学成绩。
在⽅差分析中,涉及到控制变量和随机变量以及观测变量;举例:施肥量是否会给农作物产量带来显著影响;这⾥,控制变量:施肥量,观测变量:农作物产量,随机变量:天⽓、温度……单因素分析⽬的:分析单⼀控制因素影响下的多组样本的均值是否存在显著性差异。
适⽤条件:正态性,每个⽔平下的因变量应服从正态分布;同⽅差性,各组之间的具有相同的⽅差;独⽴性,各组之间是相互独⽴的。
案例分析:案例描述:在某⼀公司下,分析⼴告形式对销售额的影响。
(数据来源:《统计分析与SPSS的应⽤》(第五版)薛薇第六章)题⽬分析:在题⽬中,⼴告形式不⾄两种,没办法⽤两独⽴样本t检验分析形式和销售额之间的显著性差异,同时,只有⼀个控制因素,所以采⽤⽅差分析中的单因素分析。
提出原假设:⼴告形式和销售额之间不存在显著性差异。
界⾯操作步骤:分析—⽐较均值—单因素ANOVA关键步骤截图:分清楚因变量列表和因⼦;因⼦:控制变量,因变量列表:观测变量结果分析:单因素⽅差分析销售额平⽅和df均⽅F显著性组间5866.08331955.36113.483.000组内20303.222140145.023总数26169.306143分析:平⽅和:组间离差平⽅和(SSA)是由控制变量的不同⽔平造成的变差,组内离差平⽅和(SSE)是由随机变量的不同⽔平造成的变差;df:组间⾃由度,在本题中根据⼴告形式的不同分为四组,所以⾃由度为k-1=4-1=3;组内⾃由度n-k=144-k=140;均⽅:即为⽅差;F=SSA/(k-1)÷(SSE/(n-k))=组间⽅差/组内⽅差,F值显著性⼤于1,说明控制变量对观测变量的影响⽐随机变量⼤,反之有效;P-值=0.00<0.05,所以拒绝原假设,认为不同的⼴告形式和地区对销售额的平均值产⽣了显著影响,不同的⼴告形式、地区对销售额的影响效应不全为0。
统计分析与SPSS的应用(第五版)课后练习答案(第6章)
《统计分析与SPSS的应用(第五版)》(薛薇)课后练习答案第6章SPSS的方差分析1、入户推销有五种方法。
某大公司想比较这五种方法有无显著的效果差异,设计了一项实验。
从应聘人员中尚无推销经验的人员中随机挑选一部分人,并随机地将他们分为五个组,第一组第二组第三组第四组第五组1)请利用单因素方差分析方法分析这五种推销方式是否存在显著差异。
2)绘制各组的均值对比图,并利用LSD方法进行多重比较检验。
(1)分析→比较均值→单因素ANOV A→因变量:销售额;因子:组别→确定。
ANOVA销售额平方和df 均方 F 显著性组之间 4 .000组内30总计34概率P-值接近于0,应拒绝原假设,认为5种推销方法有显著差异。
(2)均值图:在上面步骤基础上,点选项→均值图;事后多重比较→LSD多重比较因变量: 销售额LSD(L)(I) 组别(J) 组别平均差(I-J) 标准错误显著性95% 置信区间下限值上限第一组第二组*.048第三组.72857 .653第四组.066第五组*.000第二组第一组*.048 .0267第三组*.018 .7552第四组*.000第五组*.042第三组第一组.653第二组*.018第四组.157第五组*.000第四组第一组.066 .2162第二组*.000第三组.157 .9448第五组*.000第五组第一组*.000第二组*.042 .1267第三组*.000第四组*.000*. 均值差的显著性水平为。
可知,1和2、1和5、2和3,2和4,2和5,3和5,4和5有显著差异。
2、从两个总体中分别抽取n 1 =7 和和n 2 =6 的两个独立随机样本,经计算得到下面的方差分析表。
请补充表中单元格的两个独立随机样本,经计算得到下面的方差分析表。
请补充表中单元格“A”和单元格“B”内的计算结果。
答:已知组内均方=组内偏差平方和/自由度,所以A=11=F 统计量=组间均方/组内均方所以B==3、为研究某种降血压药的适用特点,在五类具有不同临床特征的高血压患者中随机挑选了若干志愿者进行对比试验,并获得了服用该降压药后的血压变化数据。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
S-N-K方法
目的是寻找同质子集,简单地说,各组均值首先按从小 到大的顺序排列,然后根据多重比较结果将所有的组分为若 干个子集,子集之间的各组间有差别(P值小于0.05),子集 之内的各组间无差别。
问题:分析不同地区的销售额总体上是否会随着地区人口密度的减
少(地区编号大人口密度低)而呈现某种变化趋势
Scheffe方法
当各水平下观测值个数不相等,或者想进行复杂的比较时,
或对所有可能的组合进行同步比较时,可选用此方法。这种
检验被用来检验组间均值的所有可能的线性组合,而不只是 成对组合,并控制整体显著性水平为0.05。这种方法相对比
较保守,有时候方差分析F值有显著性,用该方法进行两两比
较却找不出差异。
值存在细微差别也有可能被检验出来,但此方法对
第一类弃真错误不进行控制和调整。
Bonferroni方法
修正最小显著性差异法。用T检验完成组间成对均值的比 较,但通过设置每个检验的误差率来控制整个误差率。因此 采用此方法看到的显著值是多重比较完成后的调整值。
Tukey方法
用q检验完成各水平下观测值个数相等时组间成对均值的 比较。一定程度可以保证犯一类错误的概率总体上不增大。
当
p
p
时,拒绝原假设,即认为控制变量
不同水平下观测变量各总体的均值存在显著差异; 当 时,则不能拒绝原假设,即认为控
制变量不同水平下观测变量各总体的均值没有显 著差异
广告形式对销售额的单因素方差分析 分析
方法 一
比较均值
单因素AVOVA
因为F值对应的概率P值小于0.05,所以拒绝原
设控制变量A有k个水平,B有r个水平,每个交叉水 平下均有l个样本,则在控制变量A的水平Ai和控制 变量B的水平Bj下的第k个样本值 xijk 定义为:
xijk ai bj (ab)ij ijk
(i 1, 2,...k; j 1, 2..., r; k 1, 2..., l )
控制因素的交互作用能否对观测变量的分布产生显
著影响,进而找到有利于观测变量的最优组合。
基本思想
确定观测变量和若干个控制变量
剖析观测变量的方差 比较观测变量总离差平方和和各部分所占的比例
SST SSA SSB SSAB SSE
第一,控制变量独立作用 的影响 第二,控制变量交互作用 的影响 第三,随机因素的影响
数据变异用离均差平方和表示。
衡量同一水平下 样本数据的误差
组内误差(随机误差)
数据误差 随机误差
组间误差
系统误差
衡量控制变量不同造成的 变差
方差分析的核心是方差可分解。这里的方差是指通 过计算各观测值偏离均值的平方和再除以n-1得到。
这样,在给定n的情况下,方差就是离差平方和,
简称SST。
观测因素(观测变量):在进行方差分析时,每个控制因素水平下得到的样本数据。来自方差分析基本原理
方差分析中判断总体均值是否相等一般是通过对数据变异来 源的分析判断得到。
变异来源有两种情况:控制因素和随机因素。 控制因素:控制变量不同而造成的变异。 随机误差:在同一因素下的观察值由于抽样的随机性造成的 误差(抽样误差)。
多因素方差 分析的饱 和模型
提出零假设
H 0 : a1 a2 ak 0 b1 b2 bk 0 (ab)11 (ab)12 (ab) kr 0
H1 : a1 , a2 , ak 不全为0 b1,b2, bk 不全为0 (ab)11, (ab)12, (ab) kr 不全为0
单因素方差分析的基本步骤
单因素方差分析的基本操作
单因素方差分析的应用举例
单因素方差分析的进一步分析及应用
概念
单因素方差分析研究的是一个分类型自变量对一个
数值型因变量的影响。
例如:学历是对工资收入的影响。
基本思想
明确观测变量和控制变量
eg.前面例子中观测变量是收入;控制变量是学历
都可以使用方差分析方法去解决
方差分析概念
方差分析是检验多个总体均值是否相等的一种方法。本质上是研 究分类型自变量对数值型因变量的影响。
几个基本概念
控制因素(控制变量):在方差分析中,所要检验的对象称为因素。
其常为一个或多个离散型的分类变量。
水平:因素的不同类别或不同取值为因素的不同水平。因素的 每一个水平可以看作一个整体。
根据统计学原理,组间均方和组内均方的比值构成 F分布。给定显著性水平,通过和F分布统计量的概 率P的比较,推出总体均值是否存在显著差异。
方差分析一般应满足3个基本假设,即要求:
各个总体应服从正态分布
各个总体的方差相同
观测值是独立的。
单因素方差分析的基本思想 单因素方差分析的数学模型
单变量
因为概率P小于0.05, 所以拒绝原假设,即认 为线性模型对观测变量 有一定的解释作用
后面的几个概率中,除了交互作用中概率 大于0.05外,其余的全小于0.05,说明除了交 互作用差异不显著外,其它的都显著
多因素方差分析的非饱和模型
两因素的非饱和模型:SST=SSA+SSB+SSE 三因素的非饱和模型: SST=SSA+SSB+SSC+SSABC+SSE
SSA nij ( xi x)2
A i 1 j 1
k
r
SSB nij ( xi x)2
B i 1 j 1
r
k
SSE ( xijk xij
i 1 j 1 k 1
r
k
nij
AB 2
)
SST SSA SSB SSC SSAB SSBC SSAC SSABC SSE
的变动主要是由控制变量引起的,否则,则不是。
在水平Ai下的第j次试验的样本值
xij i ij (i 1, 2,..., k; j 1, 2,...r )
1 k i k i 1
xij可以定义为:
ai i (i 1, 2,..., k )
单因素方差分析的数学模型为 xij ai ij (i 1, 2,..., k; j 1, 2,...r)
趋势检验
在多重比较分析后得知宣传品广告效果最差,其余略有差异(先验的 结论)。这里可以对报纸、广播和体验的整体效果进行进一步的对比 分析。
先验对 比检验
所有系数之和 为0
不同广告形式下销售额总体方差齐性检验
因为P值大于0.05,所 以不能拒绝原假设, 即认为方差齐性
多重比较检验(分析哪种广告形式作用明显)
SSAB /(k 1)(r 1) MSAB SSE / kr (l 1) MSE
SSB /(r 1) MSA FB SSAB /(k 1)(r 1) MSAB
计算检验统计量观测值和概率P值
给出显著性水平 ,并作出统计决策
变量A的不同水平对观测变量产生了显著影响。
方差分析概述
单因素方差分析
多因素方差分析
协方差分析
在科学实验中常常要探讨不同实验条件或处理方法对实验结 果的影响。通常是比较不同实验条件下总体均值间的差异
举例
医学界研究几种药物对某种疾病的疗效; 农业研究土壤、肥料、日照时间等因素对某种农作物产量的影响 不同饲料对牲畜体重增长的效果等 不同广告形式、地区规模等因素对广告效果的影响等
配是否会对销售额产生影响呢?而哪种搭配方式又
可以获得最理想的销售业绩呢?
多因素方差分析的基本思想 多因素方差分析的数学模型
多因素方差分析的基本步骤
多因素方差分析的基本操作 多因素方差分析的应用举例 多因素方差分析的进一步分析及应用
概念
多因素方差分析用来研究两个及两个以上控制 变量是否对观测变量产生显著影响。它不仅能分析 多个因素对观测变量的独立影响,更能够分析多个
对四个服务行业的服务质量进行评价,较高得分 表示较高的服务质量。对航空公司、零售业、旅
馆业和汽车制造业进行的评定数据见四种不同行
业评价得分 .sav 。在显著性水平 =0.05 下,检验四 种行业质量等级的总体均值是否差异显著?你的 结论如何?
问题引出
在上一节课,我们已经研究了不同广告形式对 产品销售有显著影响,不同地区的产品销售额也存 在显著差异,然而,不同广告形式和不同地区的搭
(1)若FA的概率p< ,则拒绝原假设,即认为控制 (2)FB的概率p< ,则拒绝原假设,即认为控制变 量B的不同水平对观测变量产生了显著影响。 (3)FAB的概率p< ,则拒绝原假设,即认为控制变 量A、B的交互作用对观测变量产生了显著影响,然
后再依此对A、B的效应进行检验
分析
一般线性模型
假设,即认为不同广告形式对销售额有显著差异。
方法二
分析
比较均值
均值
单因素方
差分析一 定要选上
一、方差齐性检验
对控制变量不同水平下各观测变量总体方差是否相等进行分析 (方差分析前提条件)
二、多重比较检验 如果控制变量确实对观测变量产生了显著影响,进一步应确定
控制变量的不同水平对观测变量的影响程度如何,其中哪个水平
选择检验统计量
随机效应模型
FA SSA /(k 1) MSA SSAB /(k 1)(r 1) MSAB
固定 效 应 模 型
FA FB FAB
SSA /(k 1) MSA SSE / kr (l 1) MSE SSB /(r 1) MSB SSE / kr (l 1) MSE
