数电-精讲逻辑关系
合集下载
数电讲义--2章
1.0
VOL(max)0.5
输入标 准低电
平
0.4V
VNL
D VNH
E
V V 0.5 1.0 1.5 2.0 2.5 3.0 3.5 4.0
SL VOFF VON
SH
Vi (V)
输入标准
高电平
2. 输入特性
+VCC
1) 输入伏安特性
iI
R1 3kΩ
1
-1.6 mA
<50 uA vI A
31
B
T1
1.4 V
和边沿,T4放大。 VO随iOH变化不大。 当由i于Oi以OHH受↑:线时功性,R耗变4上的化压限。降制增,大i0,H过T大3 、会T4烧饱毁和T,4管V,O随所
功耗 1mW IOH 400 A
输出高电平时的扇出系数 3.6V
R2 750Ω 2T3 Vc2 1 3 R4
VO
+VCC
R 4 +5V 100Ω
抗干扰能力越强。 高电平噪声容限
VNH= VSH ¯ VON 。
VNH越大,输入为1态下
抗干扰能力越强。
Vo (V)
4.0 A B
3.5
3.0
VOH(min)2.5 2.4V
C
2.0
1.5
A(0V, 3. 6V) B(0.6V, 3.6V) C(1.3V, 2.48V) D(1.4V, 0.3V) E(3.6V, 0.3V)
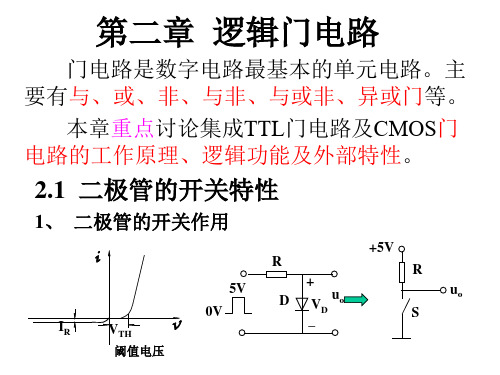
• 导通(VD>VTH) • 2、二极管的开关时间
截止5V(VDR<VT+H)
0V
D VD
uo
_
VF Vi
二极管开关状态的转换需要时间:
t1 t2
数电

2.对偶式和对偶定理 所谓对偶式就是将一个逻辑函数式Y中所有的“·”换成“+”,“+”换成“·”, “1”换成“0”,“0”换成“1”,则得到一个新的逻辑函数式Y'。 对偶定理:若是两逻辑函数式相等,则它们的对偶式也相等。
Y = A( B +
3.反演定理 将一个逻辑函数式Y中所有的“·”换成“+”,“+”换成“·”,“1”换成“0”, “0”换成“1”,原变量换成反变量,反变量换成原变量,则得到的逻辑函数 式为。将Y变为的规律称为反演定理。使用反演定理时,注意遵循如下约定: ① 需要遵守“先括号,然后乘,最后加”的运算顺序。 ② 不属于单个变量上的非号应该保留不变。 4.摩根定理 (1)摩根定理 a)定理1:或函数的非等于非的与函数,即 A + B = A B
输 入 A 0 0 1 1 B 0 1 0 1 输 出 Y 0 1 1 1
某房间的3个窗户上 某房间的 个窗户上 安装有磁控开关 , 当窗户打开时磁控 开关输出高电平 , 现在要求设计一个 电路 , 当任何一个 窗户打开时 , 该电 路输出报警信号。 路输出报警信号。
3.与门 与门是实现与运算的门电路。与运算又称为与逻辑、逻辑乘。
4. 逻辑信号 逻辑信号既可以用高电平H或是逻辑 表示有效,也可以用低电平L或是逻辑 或是逻辑1表示有效 逻辑信号既可以用高电平 或是逻辑 表示有效,也可以用低电平 或是逻辑 0表示有效。在信号为高电平 或是 有效的逻辑中,低电平 或是 表示信号无效, 表示有效。 或是1有效的逻辑中 或是0表示信号无效 表示有效 在信号为高电平H或是 有效的逻辑中,低电平L或是 表示信号无效, 而在信号为低电平L或是 有效的逻辑中,高电平H或是 表示信号无效。 或是0有效的逻辑中 或是1表示信号无效 而在信号为低电平 或是 有效的逻辑中,高电平 或是 表示信号无效。有些逻辑 图中的信号既有高电平有效的信号也有低电平有效的信号, 图中的信号既有高电平有效的信号也有低电平有效的信号,这种逻辑称为混合逻 辑。 若是用逻辑1代表高电平 代表高电平H,用逻辑0代表低电平 代表低电平L,则称为正逻辑; 若是用逻辑 代表高电平 ,用逻辑 代表低电平 ,则称为正逻辑;若是用逻 代表低电平L,用逻辑0代表高电平 代表高电平H,则称为负逻辑。 辑1代表低电平 ,用逻辑 代表高电平 ,则称为负逻辑。 代表低电平
数电 第2章 逻辑代数基础

“异或”运算的符号:
异或逻辑的真值表及其逻辑表达式:
A B 0 0 1 1 0 1 0 1
F 0 1 1 0
F A B AB AB
第2章 逻辑代数基础
A B A B A B
F F
异或门的逻辑符号
+ 1
F
第2章 逻辑代数基础
“同或”逻辑与“异或”逻辑相反,它表示当两个输入 变量相同时输出为1;相异时输出为0。 “同或”运算的符号:⊙ “同或”逻辑的真值表及其逻辑表达式:
必须注意,由原式求对偶式时,运算的优先顺序不能改
变, 且式中的非号也保持不变。 前面逻辑代数基本定律和公式,都是成对出现,而且都 是互为对偶的对偶式。 例如,已知 A(B+C)=AB+AC
则有
A+BC=(A+B)(A+C)
第2章 逻辑代数基础
2.2.3 若干常用公式
1. 合并律
AB AB A
V1 A B
&
F
( c) 中国标准
V2
二极管与门
与门的逻辑符号
第2章 逻辑代数基础
2. 或运算(逻辑加)
逻辑关系:?
或逻辑运算真值表:
A B E F
A 0 0 1 1
B 0 1 0 1
F 0 1 1 1
或逻辑实例
或逻辑可以用逻辑表达式表示:
F=A+B
第2章 逻辑代数基础
实现或逻辑的单元电路称为“或门”,其逻辑符号如左下 图所示,其中图 (a)为国际流行符号,图 (b)为 IEEE标准符号,
的B,则可以得到适用于多变量的反演律, 即
A B C A B C A B C
第2章 逻辑代数基础
数字电路基本逻辑关系及其逻辑运算

一:与逻辑和与运算
只有当决定某一种结果的所有条件都具备时,这个结果才能发生,我们把这种因果关系称为与逻辑关系,简称与逻辑。
与逻辑真值表
与逻辑运算规则
与逻辑符号
二:或逻辑和或运算
当决定某一结果的多个条件中,只要有一个或一个以上的条件具备,结果就发生,这种逻辑关系,就称为或逻辑关系,简称或逻辑。
逻辑表达式:
Y=A·B或 Y=AB
或逻辑真值表 或逻辑关系
或逻辑运算规则 或逻辑符号
或运算又称逻辑加。
用逻辑式表示为: Y=A+B
三:非逻辑和非运算
如果条件与结果的状态总是相反,则这样的逻辑关系叫做非逻辑关系,
简称非逻辑,或逻辑非。
非逻辑关系
非逻辑真值表
非运算的运算规则
1
0=-
1=-
非逻辑符号
逻辑表达式:
通常称A 为原变量,A 为反变量。
A
Y =
复合运算
四:几种常用的复合逻辑运算。
数电简明教程第一章 逻辑代数基础知识

10
第六章 脉冲产生与整形电路
概述 6.1 施密特触发器
11
12
概 述
一、逻辑代数(布尔代数、开关代数) 逻辑: 事物因果关系的规律 逻辑函数: 逻辑自变量和逻辑结果的关系
Z f ( A, B, C )
逻辑变量取值:0、1 分别代表两种对立的状态 一种状态 另一状态 高电平 真 低电平 假 是 非 有 无 … … 1 0 0 1
概述 3.1 3.2 3.3 3.4 3.5 组合电路的分析方法和设计方法 加法器和数值比较器 编码器和译码器 数据选择器和分配器 用 MSI 实现组合逻辑函数
8
第四章
概述
触发器
4.1 基本触发器 4.2 同步触发器 4.3 边沿触发器 4.4 触发器的电气特性
9
第五章
时序逻辑电路
概述 5.1 时序电路的基本分析和设计方法 5.2 计数器 5.3 寄存器和读/写存储器
( 26 )10 = 16 + 8 + 2 = 24 +23 + 21 = ( 1 1 0 1 0 )2
16 8 4 2 1
20
(3) 二-八转换: 每 3 位二进制数相当一位 8 进制数
( 0 10 101 111 ) 2 ( 257 )8
2 5 7
( 0 1 0 0 1 1 1 0 0 0 0 1. 0 0 0 1 1 0 )2 ( 2 3 4 1 . 0 6 )8
(4) 八-二转换: 每位 8 进制数转换为相应 3 位二进制数
( 31. 47 )8 ( 011 001 . 100 111
)2
)2
( 375.64 )8 ( 011 111 101 . 110 100
数字电子技术教案第3章 逻辑代数基础

重点难点:重点:逻辑函数的表达式描述方法。
难点:任意项和非完全描述函数。
方法步骤:理论讲授、例题讲解、课堂练习、课堂提问。
器材保障:多媒体电脑、投影仪、扩音设备。
教学内容与时间安排:
首先,在黑板上简单举例说明逻辑函数常见的两种描述方式——真值表、表达式,或者叫做“表现形式”。
一、描述方式之一——真值表
本次课小结:
本次课,首先学习了逻辑函数的两种描述方式——真值表和表达式,在 “表达式描述方式”这一部分内容中,又包括表达式的类型、标准的表达式;然后了解了不同描述方式之间的相互转换的方法;最后学习了非完全描述的逻辑函数和任意项。
至此,本课程的第一部分内容已经结束。对这一部分的知识结构、主要内容及学习要求做一个简单的梳理和总结。
(三) 逻辑关系、逻辑函数与数字电路
通过幻灯片上的表格说明三者之间的一一对应关系。
二、常见的逻辑运算
注意强调逻辑关系、逻辑运算和逻辑门之间的联系;注意指出三种逻辑关系、逻辑运算和逻辑门的特点;再次强调逻辑运算与普通代数运算的区别;三种逻辑运算的优先级不同;要求学生认识逻辑门的三套符号,使用国标符号。
1和0的概念是真与假、高与低、导通与截止等对应。
注意三个域之间的对应:逻辑关系、逻辑运算、逻辑门。
注意总结每种逻辑门的特点。
基本定理是等式证明、公式变换的依据。
三条规则熟练掌握应用。
总结知识点,提示知识预习。
内容
备注
《数字电子技术》课程教案
讲课题目:第05讲 逻辑代数(2) —逻辑函数的描述方式
目的要求:1、掌握逻辑函数的两种描述方式——真值表、表达式;2、理解最小项、最大项和任意项的概念。
前面提到,在逻辑函数的真值表中,自变量的每一组取值组合都代表着一个最大项和最小项。如果自变量的某个取值组合令函数值为1,则这个取值组合所代表的最小项就会出现在函数的最小项表达式中;如果自变量的某个取值组合令函数值为0,则这个取值组合所代表的最大项就会出现在函数的最大项表达式中。
难点:任意项和非完全描述函数。
方法步骤:理论讲授、例题讲解、课堂练习、课堂提问。
器材保障:多媒体电脑、投影仪、扩音设备。
教学内容与时间安排:
首先,在黑板上简单举例说明逻辑函数常见的两种描述方式——真值表、表达式,或者叫做“表现形式”。
一、描述方式之一——真值表
本次课小结:
本次课,首先学习了逻辑函数的两种描述方式——真值表和表达式,在 “表达式描述方式”这一部分内容中,又包括表达式的类型、标准的表达式;然后了解了不同描述方式之间的相互转换的方法;最后学习了非完全描述的逻辑函数和任意项。
至此,本课程的第一部分内容已经结束。对这一部分的知识结构、主要内容及学习要求做一个简单的梳理和总结。
(三) 逻辑关系、逻辑函数与数字电路
通过幻灯片上的表格说明三者之间的一一对应关系。
二、常见的逻辑运算
注意强调逻辑关系、逻辑运算和逻辑门之间的联系;注意指出三种逻辑关系、逻辑运算和逻辑门的特点;再次强调逻辑运算与普通代数运算的区别;三种逻辑运算的优先级不同;要求学生认识逻辑门的三套符号,使用国标符号。
1和0的概念是真与假、高与低、导通与截止等对应。
注意三个域之间的对应:逻辑关系、逻辑运算、逻辑门。
注意总结每种逻辑门的特点。
基本定理是等式证明、公式变换的依据。
三条规则熟练掌握应用。
总结知识点,提示知识预习。
内容
备注
《数字电子技术》课程教案
讲课题目:第05讲 逻辑代数(2) —逻辑函数的描述方式
目的要求:1、掌握逻辑函数的两种描述方式——真值表、表达式;2、理解最小项、最大项和任意项的概念。
前面提到,在逻辑函数的真值表中,自变量的每一组取值组合都代表着一个最大项和最小项。如果自变量的某个取值组合令函数值为1,则这个取值组合所代表的最小项就会出现在函数的最小项表达式中;如果自变量的某个取值组合令函数值为0,则这个取值组合所代表的最大项就会出现在函数的最大项表达式中。
数电2-逻辑函数与逻辑门

A 1=? A A 0=? A
4〉同或: A⊙ B = A B=AB + AB 相同为1 相异为0
@ Copyright 杭州电子科技大学 电子信息学院 张珣
二、逻辑函数及其表示方法
1> 真值表
例1:三个人表决一件事情,结果按“少数服从多数”的原则决定,试 建立该逻辑函数。
解:第一步:设置自变量和因变量。 第二步:状态赋值。
@ Copyright 杭州电子科技大学 电子信息学院 张珣
4 逻辑证明
(1)用简单的公式证明略为复杂的公式。 例3.1.1 证明吸收律 A + AB = A + B 证: A + AB= A(B + B) + AB = AB + AB + AB = AB + AB + AB + AB
= A(B + B) + B(A + A) = A + B
@ Copyright 杭州电子科技大学 电子信息学院 张珣
一、与或非代数系统基本逻辑关系
3、非: Y= A Y
(逻辑补) 取反
X 例: 1 = ? 0
0=? 1
A= ? A
*运算顺序:非〉与〉或
@ Copyright 杭州电子科技大学 电子信息学院 张珣
4、其他常用逻辑运算
1>与非 ——由与运算和非运算组合而成。
推广:ABC=ABC=A+B+C A+B+C=A+B+C=A B C
@ Copyright 杭州电子科技大学 电子信息学院 张珣
1、常用公式 2〉AB+AC+BC=AB+AC 证明: AB+AC+BC= AB+AC+(A+A)BC
数电-第一章 数字逻辑概论

例如: 例如:(2A.7F)H= 2×161+10×160+7×16-1+15×16-2 × × × × =(42.4960937)D 各位数的权是16的幂 各位数的权是 的幂
几种进制数之间的对应关系
十进制数 D 二进制数 B 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 10 1010 11 1011 12 1100 13 1101 14 1110 15 1111 八进制数 O 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 十六进制数 H 0 1 2 3 4 5 6 7 8 9 A B C D E F
三,八进制
数码为: ~ ;基数是8.用字母O表示 表示. 数码为:0~7;基数是 .用字母 表示. 运算规律:逢八进一, 运算规律:逢八进一,即:7+1=10. + = . 八进制数的权展开式: 八进制数的权展开式:D=∑ki×8i 例如: (207.04)O= 例如: )
2×82 +0×81+7×80+0×8-1+4 ×8-2 × × × × =(135.0625)D
= 011 (
六,十—十六进制之间的转换
将十六进制数转换成十进制数时, 将十六进制数转换成十进制数时,按权展开再 相加即可. 相加即可.
将十进制数转换成十六进制数时,可先转换成 将十进制数转换成十六进制数时, 二进制数, 二进制数,再将得到的二进制数转换成等值的十 六进制数. 六进制数.
1.2 二进制数的算术运算
二,二进制
数码为:0,1; 数码为: , ; 基数是 .用字母 表示. 基数是2.用字母B表示 表示. 运算规律:逢二进一,即:1+1=10. 运算规律:逢二进一, + = . 二进制数的权展开式: 二进制数的权展开式:D=∑ki×2i
几种进制数之间的对应关系
十进制数 D 二进制数 B 0 0000 1 0001 2 0010 3 0011 4 0100 5 0101 6 0110 7 0111 8 1000 9 1001 10 1010 11 1011 12 1100 13 1101 14 1110 15 1111 八进制数 O 0 1 2 3 4 5 6 7 10 11 12 13 14 15 16 17 十六进制数 H 0 1 2 3 4 5 6 7 8 9 A B C D E F
三,八进制
数码为: ~ ;基数是8.用字母O表示 表示. 数码为:0~7;基数是 .用字母 表示. 运算规律:逢八进一, 运算规律:逢八进一,即:7+1=10. + = . 八进制数的权展开式: 八进制数的权展开式:D=∑ki×8i 例如: (207.04)O= 例如: )
2×82 +0×81+7×80+0×8-1+4 ×8-2 × × × × =(135.0625)D
= 011 (
六,十—十六进制之间的转换
将十六进制数转换成十进制数时, 将十六进制数转换成十进制数时,按权展开再 相加即可. 相加即可.
将十进制数转换成十六进制数时,可先转换成 将十进制数转换成十六进制数时, 二进制数, 二进制数,再将得到的二进制数转换成等值的十 六进制数. 六进制数.
1.2 二进制数的算术运算
二,二进制
数码为:0,1; 数码为: , ; 基数是 .用字母 表示. 基数是2.用字母B表示 表示. 运算规律:逢二进一,即:1+1=10. 运算规律:逢二进一, + = . 二进制数的权展开式: 二进制数的权展开式:D=∑ki×2i
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
表2 或逻辑真值表
A 0 0 1 1
B 0 1 0 1
P 0 1 1 1
A+1=1;A+0=A;A+A=A。
口诀:见1出1
三种基本逻辑关系
3、非逻辑和非运算 定义:如果某一事件的发生取决于条件的否定,即事 件与事件发生的条件之间构成矛盾,则这种因果关系称为 “非”逻辑。 非逻辑的逻辑函数表达式:P= A。
0•0=0;0•1=0;
表1 与逻辑真值表
A 0 0 1 1
B 0 1 0 1
P 0 0 0 1
1•0=0;1•1=1。
逻辑乘的一般形式是: A•1=1;A•0=0;A•A=A。
逻辑函数的真值表是描述逻辑 函数的一种直观的描述方法。
口诀:全1为1
三种基本逻辑关系
2、或逻辑和或运算 定义:如果决定某一事件是否发生的多个条件中,只 要有一个或一个以上条件成立,事件便可发生,则这种因 果关系称之为“或”逻辑。 或逻辑的逻辑函数表达式:P=A+B。
P 1 0 0 0
A B
P
图5 或非逻辑符号
口诀:全0为1
复合逻辑关系
3、与或非逻辑和与或非运算 与或非逻辑函数的表达式:
P AB +CD
A B C D & &
E
A B C D
& ≥1 P
≥1
F
P
图 6 与或非逻辑符号
图 7 与或非的等效电路
复合逻辑关系
4、异或逻辑和异或运算 异或逻辑函数表达式:
逻辑代数的基本逻辑关系
主讲人:张老师
主讲内容
1 逻辑代数的介绍
2 三种基本逻辑关系
3 复合逻辑关系 4 总结
逻辑代数的介绍
逻辑代数又叫布尔代数,也称开关代数,是描述 客观事物逻辑关系的数学方法。
1847年,英国数学家乔治·布尔提出了用数学分析方法表示命题陈 述的逻辑结构,并成功地将形式逻辑归结为一种代数演算,从而诞生了 著名的“布尔代数”。 1938年,克劳德·向农将布尔代数应用于电话继电器的开关电路, 提出了“开关代数”。
P 1 0 0 1
A B
=1
P
图9 同或逻辑符号
口诀:相同为1
例1 写出图11所示逻辑图的逻辑函数表达式,并 列出真值表。
&
AB
1
A
1
A
&
F
AB 表9 逻辑函数真值表
B
1
B
图11 逻辑电路图
解:(1)表达式:F=AB+A B
(2)真值表:如表9所示 F=AB+A B=A ⊙ B
A 0 0 1 1
A
B E (a) 电路图
P
A B
≥1
(b)逻辑符号
P
L=AB
图2 或逻辑
A B E
A B E
P
P
A、B都断开,灯不亮。
A B E
A断开、B接通,灯亮。
A B E
P
P
A接通、B断开,灯亮。
A、B都接通,灯亮。
两个开关只要有一个接通, 灯就会亮。逻辑表达式为:
P=A+B
或运算也叫逻辑加,它的 逻辑运算规则是: 0+0=0;0+1=1; 1+0=1;1+1=1。 逻辑加的一般形式是:
A E (a) 电路图 B P
A B
&
(b)(b) 逻辑符号 逻辑符号
P
L=AB
图1 与逻辑
A E
B P E
A
B P
A、B都断开,灯不亮。
A E B P
A断开、B接通,灯不亮。
A E B P
A接通、B断开,灯不亮。
两个开关必须同时接通,灯才亮。逻辑表达式 为:
A、B都接通,灯亮。
P=A•B
与运算也叫逻辑乘,它的 运算规则是:
1、与非逻辑和与非运算
与非逻辑函数的表达式:
表4 与非逻辑函数真值表
P AB
&
P
A 0 0 1 1
B 0 1 0 1
P 1 1 1 0
A B
图4 与非逻辑符号
复合逻辑关系
2、或非逻辑和或非运算 或非逻辑函数的表达式:
表5 或非逻辑函数真值表
P A+B
≥1
A 0 0 1 1
B 0 1 0 1
B 0 1 0 1
P 1 0 0 1
例2 画出逻辑函数表达式的P= A BC+ AB C+ ABC 真值表。 解:真值表:如表8所示 3个变量输入
表8 逻辑函数真值表
A 0 0 0 0 1 1 1 1
B 0 0 1 1 0 0 1 1
C 0 1 0 1 0 1 0 1
P 0 0 0 1 0 1 0 1
23个组合
23 个输出
例3 写出图10所示逻辑图的逻辑函数表达式。
A B
&
AB
C
&
BC
1P&来自AC图10 逻辑电路图
解:表达式:P=AB+BC+AC 化简 P=AB+BC+AC P= A BC+ AB C+ ABC
总结:
三种基本逻辑 关系
与逻辑和与运算
或逻辑和或运算
非逻辑和非运算
重点内容
与非逻辑和与非 运算 或非逻辑和或非 运算
逻辑代数中只存在0和1两个数字,用来描述两种 完全相反的逻辑状态,不代表具体数值。 例如:高电平和低电平,光信号的有或无,开关 的闭合与断开等。
三种基本逻辑关系
逻辑代数中有三种最基本的逻辑,分别是与逻辑、或 逻辑和非逻辑。与其相对应的运算有三种:与运算、或运 算和非运算。 1、与逻辑和与运算 定义:如果决定某一事件发生的多个条件必须同时具 备,事件才能发生,则这种因果关系称之为“与”逻辑。 表达式为:P=A•B。常用•,∩,∧,&及and表示相与。
表6 异或逻辑函数真值表
P A B AB AB
A B
图8 异或逻辑符号
A 0 0 1 1
B 0 1 0 1
P 0 1 1 0
=1
P
口诀:相异为1
复合逻辑关系
5、同或逻辑和同或运算 同或逻辑函数表达式:
表7 同或逻辑函数真值表
P A B AB AB
A 0 0 1 1
B 0 1 0 1
R E 电路图
图3 非逻辑
A
P
A
1
逻辑符号
P
表3 非逻辑真值表
R E A
A 0 1
P 1 0
P
A接通,灯灭。
非逻辑的运算规则是: 0=1;1=0。
R E A P
逻辑加的一般形式是:
A =A;A+A =1;A•A =0
A断开,灯亮。
口诀:0为1, 1为0
复合逻辑关系
与、或、非三种基本逻辑按不同的方式组合,还可 以构成与非、或非、与或非、同或、异或等逻辑,统称 为复合逻辑。
复合逻辑关系
异或逻辑和异或 运算 同或逻辑和同或 运算
表10 各种逻辑关系的表达式和逻辑符号 逻辑关系 与 或 非 与非 或非 与或非 异或 同或 逻辑表达式 P=AB P=A+B P= A AB 逻辑符号
&
(b) 逻辑符号 ≥1
&
&
A +B
AB+CD A⊕ B A⊙ B
& &
≥1
≥1
=1
=1
