直方图均衡化原理及编码实现
图像处理中直方图均衡化的使用教程

图像处理中直方图均衡化的使用教程图像处理中的直方图均衡化是一种常用的增强图像对比度的方法。
通过对图像的像素值进行重新分布,直方图均衡化可以使图像中的明暗区域更具有对比度,从而提高图像的质量和清晰度。
本文将介绍直方图均衡化的原理、应用场景以及具体的步骤。
1. 直方图均衡化的原理直方图均衡化的原理基于对图像的灰度级进行重新分布。
它通过将原始图像的像素值映射到新的像素值上,使得直方图在整个灰度范围内得到均匀分布。
这样就能够增强图像中的低对比度区域,提高图像的视觉效果。
2. 直方图均衡化的应用场景直方图均衡化在图像处理领域有着广泛的应用。
下面列举了一些常见的应用场景:- 增强图像的对比度:直方图均衡化可以使得图像中的亮度值更加均匀分布,提高图像的对比度,使得图像变得更加清晰。
- 增强图像的细节:直方图均衡化通过增强图像中的低对比度区域,可以使得细节更加显著,提高图像的可视化效果。
- 降低图像的噪声:直方图均衡化可以将图像中的噪声分布均匀化,从而减少噪声对图像质量的影响。
3. 直方图均衡化的步骤下面是使用直方图均衡化对图像进行处理的具体步骤:步骤 1: 将彩色图像转换为灰度图像如果原始图像是彩色图像,我们需要将其转换为灰度图像。
这是因为直方图均衡化是针对灰度级进行处理的。
步骤 2: 计算原始图像的像素值分布使用图像处理工具,计算原始图像中每个像素值的出现频率。
这样可以得到一个直方图,该直方图显示了原始图像中像素值的分布情况。
步骤 3: 计算累积分布函数通过对原始图像的直方图进行累积求和,得到一个累积分布函数。
该函数显示了每个像素值的累积出现频率。
步骤 4: 计算新的像素值根据累积分布函数,计算每个像素值的新的映射像素值。
这个计算公式可以根据具体的图像处理工具而有所不同。
步骤 5: 创建均衡化后的图像使用新的像素值替换原始图像中的像素值,将得到的图像称为均衡化后的图像。
4. 注意事项在使用直方图均衡化时,需要考虑以下几个注意事项:- 直方图均衡化可能会改变图像的整体亮度。
数字图像处理实验3图像直方图与均衡化

实验三图像直方图与均衡化一、实验原理离散图像用直方图表示该图像中各个不同灰度级像素出现的相对频率。
灰度直方图是简单且实用的工具,对图像的采集、处理和分析都可以有效地利用直方图。
灰度直方图反映了数字图像中的每一灰度级与其出现的频率间的关系。
直方图均衡化是通过对原图形进行某种变换,使图像的直方图变为均匀分布的直方图,从而达到增强的效果。
二、实验设备MATLAB软件三、实现程序:pic=imread('football.jpg');imshow(pic)imwrite(rgb2gray(PS),'football.bmp');pic=rgb2gray(pic);figure,imshow(pic)[m,n]=size(pic);S0=zeros(1,256);for k=0:255S0(k+1)=length(find(pic==k))/(m*n);endfigure,bar(0:255,S0,'g')S1=zeros(1,256);for i=1:256for j=1:iS1(i)=S0(j)+S1(i);endendS2=round(S1*256);for i=1:256S0eq(i)=sum(S0(find(S2==i)));endfigure,bar(0:255,S0eq,'b')Img=pic;for i=0:255Img (find(pic==i))=S2(i+1);endfigure,imshow(Img);四、运行结果:原图像的直方图均衡化后图像的直方图原图像均衡化后的图像。
C语言数字图像处理之直方图均衡化

C语⾔数字图像处理之直⽅图均衡化本⽂实例为⼤家分享了C语⾔直⽅图均衡化的具体代码,供⼤家参考,具体内容如下原理直⽅图均衡化(Histogram Equalization) ⼜称直⽅图平坦化,实质上是对图像进⾏⾮线性拉伸,重新分配图像象元值,使⼀定灰度范围内象元值的数量⼤致相等。
这样,原来直⽅图中间的峰顶部分对⽐度得到增强,⽽两侧的⾕底部分对⽐度降低,输出图像的直⽅图是⼀个较平的分段直⽅图:如果输出数据分段值较⼩的话,会产⽣粗略分类的视觉效果。
直⽅图是表⽰数字图像中每⼀灰度出现频率的统计关系。
直⽅图能给出图像灰度范围、每个灰度的频度和灰度的分布、整幅图像的平均明暗和对⽐度等概貌性描述。
灰度直⽅图是灰度级的函数, 反映的是图像中具有该灰度级像素的个数, 其横坐标是灰度级r, 纵坐标是该灰度级出现的频率( 即像素的个数) pr( r) , 整个坐标系描述的是图像灰度级的分布情况, 由此可以看出图像的灰度分布特性, 即若⼤部分像素集中在低灰度区域, 图像呈现暗的特性; 若像素集中在⾼灰度区域, 图像呈现亮的特性。
灰度数字图像是每个像素只有⼀个采样颜⾊的图像。
这类图像通常显⽰为从最暗⿊⾊到最亮的⽩⾊的灰度。
灰度图像与⿊⽩图像不同,在计算机图像领域中⿊⽩图像只有⿊⽩实现流程:1)统计每个灰度级像素点的个数2)计算灰度分布密度3)计算累计直⽅图分布4)累计分布取整,保存计算出来的灰度映射关系处理图⽚规格800*600 8位灰度单通道原图直⽅图均衡化分析:本次实验中,我故意把原图调暗,进⾏直⽅图均衡化后可以明显感受到整幅图像亮度增⼤了,⽽且某些细节⽅⾯更加突出。
出现问题最初进⾏直⽅图均衡化时,输出结果如下:经分析,是没有对数组初始化置零导致的。
Hist数组是进⾏⼀个统计像素点个数的数组,最初倘若不置零,结果必然毫⽆意义。
故⽽添加数组内存置零的操作:经测试,问题解决。
附代码#include <stdio.h>#include <stdlib.h>#include <memory.h>#define height 600#define width 800typedef unsigned char BYTE; // 定义BYTE类型,占1个字节int main(void){FILE *fp = NULL;//BYTE Pic[height][width];BYTE *ptr;BYTE **Pic = new BYTE *[height];for (int i = 0; i != height; ++i){Pic[i] = new BYTE[width];}fp = fopen("weiminglake_huidu.raw", "rb");ptr = (BYTE*)malloc(width * height * sizeof(BYTE));//创建内存for (int i = 0; i < height; i++){for (int j = 0; j < width; j++){fread(ptr, 1, 1, fp);Pic[i][j] = *ptr; // 把图像输⼊到2维数组中,变成矩阵型式ptr++;}}fclose(fp);int hist[256];float fpHist[256];float eqHistTemp[256];int eqHist[256];int size = height *width;int i, j;memset(&hist, 0x00, sizeof(int) * 256);memset(&fpHist, 0x00, sizeof(float) * 256);memset(&eqHistTemp, 0x00, sizeof(float) * 256);for (i = 0; i < height; i++) //计算差分矩阵直⽅图直⽅图统计每个灰度级像素点的个数{for (j = 0; j < width; j++){unsigned char GrayIndex = Pic[i][j];hist[GrayIndex] ++;}}for (i = 0; i< 256; i++) // 计算灰度分布密度{fpHist[i] = (float)hist[i] / (float)size;}for (i = 0; i< 256; i++) // 计算累计直⽅图分布{if (i == 0){eqHistTemp[i] = fpHist[i];}else{eqHistTemp[i] = eqHistTemp[i - 1] + fpHist[i];}}//累计分布取整,保存计算出来的灰度映射关系for (i = 0; i< 256; i++){eqHist[i] = (int)(255.0 * eqHistTemp[i] + 0.5);}for (i = 0; i < height; i++) //进⾏灰度映射均衡化{for (j = 0; j < width; j++){unsigned char GrayIndex = Pic[i][j];Pic[i][j] = eqHist[GrayIndex];}}fp = fopen("output.raw", "wb");for (i = 0; i < height; i++){for (j = 0; j < width; j++){fwrite(&Pic[i][j], 1, 1, fp);}}fclose(fp);return 0;}以上就是本⽂的全部内容,希望对⼤家的学习有所帮助,也希望⼤家多多⽀持。
直方图均衡化的原理和作用

直方图均衡化的原理和作用直方图均衡化是一种常见的图像处理技术,用于增强图像的对比度和视觉效果。
它的原理是通过重新分布图像的灰度级别,使得图像中的像素灰度值分布更加均匀,从而改善图像的视觉效果。
在进行直方图均衡化时,首先需要获取图像的灰度直方图,然后根据灰度直方图的累积概率密度函数对图像的像素进行重新分配。
直方图均衡化的作用主要体现在以下几个方面:1. 增强图像的对比度:直方图均衡化可以有效地增强图像的对比度,使得图像中不同区域的灰度级别更加明显,从而使得图像的细节更加清晰。
2. 提高图像的视觉效果:通过直方图均衡化,图像的灰度级别分布更加均匀,可以使得图像看起来更加自然和真实,同时增强了图像的视觉效果,使得观看者更容易理解和分析图像内容。
3. 抑制背景噪声:在图像处理中,背景噪声往往会影响图像的清晰度和质量。
通过直方图均衡化可以有效地抑制背景噪声,使得图像更加清晰和易于分析。
4. 增强图像的细节:直方图均衡化可以增强图像的细节,使得图像中的纹理和结构更加清晰和突出,同时也能够凸显出图像中的一些微弱的特征。
直方图均衡化的原理是基于图像的灰度级别分布的重新分配,其具体操作过程如下:1. 获取图像的灰度直方图:首先需要对图像进行灰度化处理,然后统计不同灰度级别的像素点数量,从而得到图像的灰度直方图。
2. 计算灰度直方图的累积概率密度函数:根据图像的灰度直方图,可以计算出每个灰度级别对应的累积概率密度函数,即将原始的灰度级别映射到新的灰度级别上。
3. 根据累积概率密度函数对像素进行重新分配:根据计算得到的累积概率密度函数,可以将图像中的每个像素的灰度级别重新映射到新的灰度级别上,从而得到均衡化后的图像。
通过以上操作,可以实现直方图均衡化,从而改善图像的对比度和视觉效果。
需要注意的是,直方图均衡化可能会增强图像中的噪声和细小的纹理,因此在实际应用中需要结合具体的图像特性进行调整,以达到最佳的效果。
总之,直方图均衡化是一种有效的图像处理技术,通过重新分配图像的灰度级别,可以增强图像的对比度,改善图像的视觉效果,并抑制背景噪声,使得图像更加清晰和易于分析。
图像编码中的直方图均衡化方法探究

图像编码中的直方图均衡化方法探究一、引言图像编码是一种将图像转换为数字数据以便存储或传输的过程。
在图像编码中,直方图均衡化是一种常用的图像增强方法。
通过对图像的像素值进行变换,直方图均衡化可以增强图像的对比度和细节,并改善图像的视觉效果。
本文将探讨直方图均衡化方法在图像编码中的应用。
二、直方图均衡化的基本原理直方图均衡化是通过对图像像素值进行变换,将原始图像的像素值分布转换为均匀分布,以实现对比度的增强。
在直方图均衡化过程中,首先需要计算图像的灰度直方图,即统计图像中各个灰度级别的像素数量。
然后,通过归一化直方图将像素值映射到[0,1]的范围内。
最后,通过累积概率函数将归一化后的直方图变换为均匀分布的直方图。
三、直方图均衡化的优点直方图均衡化具有以下几个优点:1.增强对比度:直方图均衡化可以通过增大灰度级别之间的差异来增强图像的对比度,使得图像中的细节更加清晰。
2.增强细节:直方图均衡化可以通过增大较低灰度级别的像素值来提高图像中的细节。
这对于一些细节丰富但对比度较低的图像特别有效。
3.适应不同场景:直方图均衡化可以适应不同场景下的图像,不受光照条件的影响。
它可以将图像的整体亮度分布进行调整,以适应不同的光照条件。
四、直方图均衡化的应用直方图均衡化在图像编码中有着广泛的应用。
下面将介绍两种常见的图像编码方法,以及在这两种方法中直方图均衡化的应用。
1.离散余弦变换(DCT)编码离散余弦变换(DCT)是一种基于空间频率的图像编码方法。
在DCT编码中,直方图均衡化可以应用于DCT系数的量化过程。
通过对DCT系数的直方图进行均衡化处理,可以提高编码后的图像的清晰度和对比度。
2.小波变换编码小波变换是一种多分辨率分析方法,常用于图像压缩编码中。
在小波变换编码中,直方图均衡化可以应用于小波系数的量化过程。
通过对小波系数的直方图进行均衡化处理,可以增强编码后的图像的细节和对比度,并减少编码后的图像中的噪声。
五、直方图均衡化方法的改进传统的直方图均衡化方法存在一些问题,比如在图像具有大片连续区域相同灰度的情况下,会产生明显的噪点。
Python图像直方图、高斯滤波、直方图均衡化的结果及基本原理

Python图像直⽅图、⾼斯滤波、直⽅图均衡化的结果及基本原理⼀、图像直⽅图1、基本原理 直⽅图的定义:图像的直⽅图⽤来表⽰该图像像素值的分布情况。
⽤⼀定数⽬的⼩区间(bin)来指定表征像素值的范围,每个⼩区间会得到落⼊该⼩区间表⽰范围的像素数⽬。
绘制图像直⽅图: ⼀幅数字图像在[0,G]的范围内总共有L个灰度级,其直⽅图定义为下列离散函数:h(r k) = n k 式⼦中,r k 是区间[0,G]内的第k级灰度,n k为图像中出现r k 这种灰度级的像素数量。
对于uint8类图像,G的值为255;对于uint16类图像,G的值为65535;对于浮点图像,G的值为1.0。
注意,对于uint8类和uint16类图像,G=L-1。
图像的直⽅图可以使⽤ hist() 函数绘制。
hist() 函数的第⼆个参数指定⼩区间的数⽬。
需要注意的是,因为 hist() 只接受⼀维数组作为输⼊,所以我们在绘制图像直⽅图之前,必须先对图像进⾏压平处理。
flatten() ⽅法将任意数组按照⾏优先准则转换成⼀维数组。
2、相关代码:(参考课本)from array import arrayfrom PIL import Imagefrom pylab import *# 添加中⽂字体⽀持from matplotlib.font_manager import FontPropertiesfont = FontProperties(fname=r"c:\windows\fonts\SimSun.ttc", size=14)im = array(Image.open('../images/02.jpg').convert('L')) # 打开图像,并转成灰度图像figure()subplot(121)gray()contour(im, origin='image')axis('equal')axis('off')title(u'图像轮廓', fontproperties=font)subplot(122)hist(im.flatten(), 128)title(u'图像直⽅图', fontproperties=font)plt.xlim([0, 260])plt.ylim([0, 11000])show()3、运⾏结果:⼆、⾼斯滤波1、基本原理 ⾼斯滤波的定义:它是⼀种线性平滑滤波,能够有效的抑制⾼斯噪声,⼴泛应⽤于图像处理的减噪过程。
直方图均衡化(histogramequalization)

直⽅图均衡化(histogramequalization)⼀. 原理直⽅图均衡化是想要将聚集在某⼀区间内分布的灰度值,变为均匀的在所有区间内分布。
为了达到这⼀⽬的,我们需要找出⼀个函数T,将r(原图像灰度)映射到s(新图像灰度)上。
同时,由于不想将图像反转,我们需要保证函数单调不减(若需要逆运算,则要严格单调递增)s=T(r)设p r(r)为r的概率分布函数,p s(s)为s的概率分布函数,则两者关系如下p s(s)=p r(r)|dr ds|也就是说,T(r)这个函数现在要满⾜条件:单调递增值域范围为[0,L-1]p s(s)为⼀个常函数(表⽰每⼀个灰度值的概率都相等)现在给出⼀个函数(⾄于为什么是这个函数,我也不知道啊,哪位看官可以帮忙推导⼀下QAQ):s=T(r)=(L−1)∫r0p r(w)dw我们将逐步证明,以上三点成⽴由于此函数为积分所得,因此函数单调递增由于p r(r)为概率密度函数,因此,积分区间为[0,1],乘以常数,区间为[0,L-1]推导过程:ds=dT(r)=d((L−1)∫r0p r(w)dw)=(L−1)p r(r)drp s(s)=p r(r)|drds|=pr(r)|1(L−1)p r(r)|=1L−1此时p s(s)为⼀个均匀密度函数,符合对于离散值,计数每个不⼤于r的概率和,就是这个r对应的ss k=T(r k)=(L−1)k∑j=0p r(r j)⼆. 代码img = imread("14.jpeg");r = img(:,:,1);g = img(:,:,2);b = img(:,:,3);p = stat(r);map = cal(p);img_equa = my_hist_equation(r,map); % 画图%原图subplot(331)imshow(r);title('原图');subplot(332)imhist(r);title('原图直⽅图');%⾃⼰的直⽅图均衡化图subplot(334)imshow(img_equa);title('my直⽅图均衡化图');subplot(335)imhist(img_equa);title('my直⽅图均衡化直⽅图'); subplot(336)plot((0:255)/255,map/255);title('my函数');%标准的直⽅图均衡化图[std_img,T] = histeq(r);subplot(337)imshow(std_img);title('标准直⽅图均衡化图');subplot(338)imhist(std_img);title('标准直⽅图均衡化图直⽅图'); subplot(339)plot((0:255)/255,T);Processing math: 100%title('std函数');figureplot((0:255)/255,map/255);figureplot((0:255)/255,T);%计算图像的分布function p=stat(img)[r,c] = size(img);p = linspace(0,0,256);for i=1:1:rfor j=1:1:cp(img(i,j)+1)= p(img(i,j)+1)+1;endendp = p/(r*c);end%计算r与s的对应关系,矩阵坐标为r,值为s(动态规划) function s=cal(probality)s=probality;l = length(probality);for i=2:ls(i) = s(i-1)+s(i);ends = round(s*255);end%将图⽚根据映射函数,映射function img_equa=my_hist_equation(img,map)[r,c] = size(img);img_equa = zeros(r,c);for i=1:rfor j=1:cimg_equa(i,j) = map(img(i,j)+1);endendimg_equa = uint8(img_equa);end放⼤我的映射函数图⽚为:matlab⾃建的映射函数为:对⽐两个映射函数可以看出来,⾃⼰实现的为⽐较连续的,⽽matlab⾃建的为阶段性的。
编程实现直方图均衡化
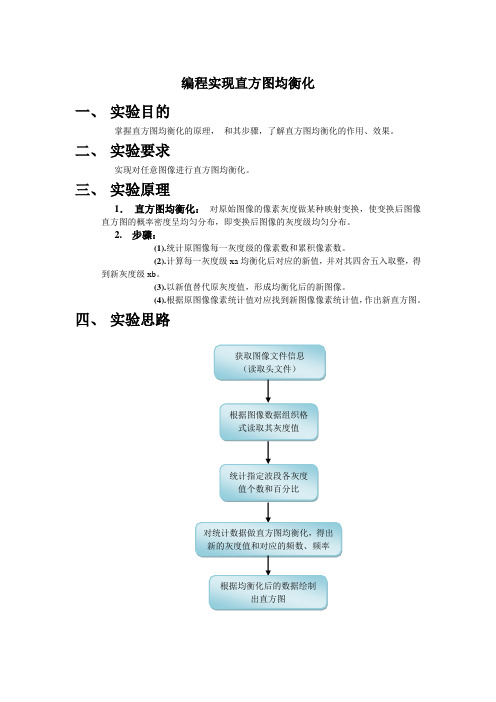
编程实现直方图均衡化一、实验目的掌握直方图均衡化的原理,和其步骤,了解直方图均衡化的作用、效果。
二、实验要求实现对任意图像进行直方图均衡化。
三、实验原理1.直方图均衡化:对原始图像的像素灰度做某种映射变换,使变换后图像直方图的概率密度呈均匀分布,即变换后图像的灰度级均匀分布。
2. 步骤:(1).统计原图像每一灰度级的像素数和累积像素数。
(2).计算每一灰度级xa均衡化后对应的新值,并对其四舍五入取整,得到新灰度级xb。
(3).以新值替代原灰度值,形成均衡化后的新图像。
(4).根据原图像像素统计值对应找到新图像像素统计值,作出新直方图。
四、实验思路五、 实验步骤1.新建项目文件:本实验选用的语言是C#,开发工具是VisualStudio2010,通过“文件—新建—项目—C#—Windows 窗体应用程序”,命名“直方图均衡化”即可;2.编写代码:由实验思路中的思维导图可得知,本实验步骤与“绘制直方图实验非常类似”,只是中间加了对原始图像灰度值统计数据进行了均衡化处理这一步骤,因此,只需在它的基础上进行改动和添加部分代码即可,具体如下:(1).编写头文件读取代码:由于以前的实验已有该代码,那么只需,导入其所在的“.cs ”类文件即可;(2).编写读取图像灰度值代码:将“绘制任意图像灰度值”实验该部分功能“.cs ”类文件导入即可;(3).编写统计灰度值代码:载入该功能所在“.cs ”类文件即可;(4).编写直方图均衡化代码:由实验原理里的直方图均衡化步骤可知它对应的代码部分应该有:统计像素累计数,这个只需利用已有的灰度值及其频数所在的Hashtable 哈希表数据即可;将原始灰度级映射到新的值,只需编写一个 对应方法,再对新的灰度级频数进行统计即可,具体代码将后文;(5).编写绘制直方图代码:导入已有的代码所在“.cs ”类文件即可。
3.编译与调试:通过VS2010断点等调试工具,可查看、排除程序错误,无语法、逻辑错误后,编译生成程序文件即可;4.运行程序查看结果:运行程序,加载实验数据,查看绘制出的直方图,然后再通过ENVI 的“Enhance-Interactive Stretching ”工具选择“SretchType ”为“Equalization ”执行后显示的直方图对比,看是否准确;六、 结果与分析1. 结果程序界面()01kja a j L h x N =-∑2.分析在对灰度级进行映射转换时一定要进行四舍五入运算,否则会有误差。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
//行
pPixelLine[y] = T[pPixelLine[y]];
}
} // 显示直方图均衡化后图像 cvNamedWindow("dst"); cvShowImage("dst", dst);
// 直方图均衡化后图像的直方图 IplImage *dstHistImg = cvCreateImage(cvSize(256, 200), 8, 3); cvSet(dstHistImg, CV_RGB(255, 255, 255)); plotHist1D(dst, dstHistImg, CV_RGB(100, 100, 100)); // 画直方图 cvNamedWindow("dstHist"); cvShowImage("dstHist", dstHistImg);
// 1.计算直方图 int bins = DEPTH; int sizes[] = {bins}; CvHistogram* hist = cvCreateHist(1, sizes, CV_HIST_ARRAY); cvCalcHist(&dst, hist); cvNormalizeHist(hist, 1); //归一化
原始图片:
直方图:
直方图均衡化后结果:
直方图:
OpenCV 源码:
/**********************************************************/ // 说明:直方图参考例程 // 作者:Mark // 时间:6.4.2011 /**********************************************************/ #include <cv.h> #include <highgui.h> #include "histogram.h"
归一化: 概率密度函数为:
概率分布函数为:
������
A0 = ∫ ������������(������)������������0源自p(������)=
������������(������) ������0
1 ������
P(������)
=
A0
∫
0
������������(������)������������
其中:
T′(������) = ds/dr
所以,当������������的分子分母只差一个比例常数时,������������就恒定。即,
T′(������)
=
������ ������0
������������(������)
所以:
其中
������ ������
s
=
T(������)
=
������0
在离散情况下
其中
s = T(r) = ������������(������������)
������为图像中总像素个数。
������(������������)
=
k
∑
������������ ������
������=0
编码实现(OpenCV): 1. 计算图像直方图,并归一化 2. 计算变换函数 s = T(������) 3. 根据 s = T(������) 计算新的灰度值 s
#define DEPTH 256
int main(void) {
IplImage *src = cvLoadImage("D:\\picture\\素材\\9.jpg", CV_LOAD_IMAGE_GRAYSCALE);
IplImage *dst = cvCloneImage(src);
// 显示原始图片 cvNamedWindow("src"); cvShowImage("src", src);
// 2.计算变换函数 s=T(r) double val = 0.0; uchar T[DEPTH] = {0}; for(int index = 0; index < DEPTH; index++) {
val += cvQueryHistValue_1D(hist, index); T[index] = (uchar)(val*255); }
// 3.灰度变换
uchar* pPixelLine = NULL;
for(int x = 0; x < dst->height; x++) {
//列
pPixelLine = (uchar *)(dst->imageData + x*dst->widthStep);
for(int y = 0; y < dst->width; y++) {
设变换:
s = T(������) 为斜率有限的非减连续可微函数,它将输入图像A(������, ������)转换为输出图像 B(������, ������)。 输入图像的直方图为H������(������)与输出图像的直方图为H������(������)之间的关系可由如 下过程导出
根据直方图的含义,经过灰度变换后对应的小面积元相等
cvWaitKey(0); cvReleaseImage(&src); cvReleaseImage(&dst); cvReleaseImage(&srcHistImg); cvReleaseImage(&dstHistImg); cvReleaseHist(&hist); cvDestroyAllWindows(); return 0; }
直方图均衡化
Author:Mark Date:6.4.2011
原理: 直方图均衡化是通过灰度变换将一幅图像转换为另一幅具有均衡直方图,即
在每个灰度级上都具有相同的象素点数的过程。
对图像A(������, ������),灰度范围为[0, ������],其图像的直方图为H������(������),图像 A 的总像 素点数为:
解得:
������������(������)������������ = ������������(������)������������
������������
=
������������(������) ������������/������������
=
������������(������) ������′(������)
// 原始图像直方图 IplImage *srcHistImg = cvCreateImage(cvSize(256, 200), 8, 3); cvSet(srcHistImg, CV_RGB(255, 255, 255)); plotHist1D(src, srcHistImg, CV_RGB(100, 100, 100)); // 画直方图 cvNamedWindow("srcHist"); cvShowImage("srcHist", srcHistImg);
∫
0
������������(������)������������
=
C������(������)
1 ������
P(������)
=
A0
∫
0
������������(������)������������
为了使 s 的取值范围为[0, ������]:
C=L
由此得,使直方图均衡化的灰度变换函数是概率分布函数。
