单位根检验
单位根检验

单位根检验单位根检验是一种用于检验指数时间序列是否稳定的方法。
在经济学中,许多变量都是随时间变化的,如股票价格、货币汇率、通货膨胀率等,而这些变量都可以被视为时间序列。
但是,这些时间序列是否稳定是一个重要的问题。
因为如果一个时间序列是不稳定的,那么它的预测结果就是不可靠的。
什么是单位根?单位根是指一个数学方程中的根等于1的根。
在统计学中,我们通常使用单位根来检验时间序列的稳定性。
如果时间序列有一个单位根,那么它就是不稳定的。
因此,我们需要通过时间序列的单位根检验来确定它是否是稳定的。
单位根检验是基于一个叫做“随机游走”的经济学理论的基础上的。
随机游走是指一个随机变量在未来的状态完全是随机的。
如果一个时间序列是随机游走的,那么它就是不稳定的。
因此,我们需要通过检验这个序列是否是随机游走来确定它是否是稳定的。
单位根检验的主要步骤如下:第一步:确定时间序列的类型。
我们需要确定这个时间序列的具体类型,是属于随机游走类型还是平稳类型,或者是介于两者之间的。
第二步:选择一种统计方法进行检验。
单位根检验有许多种不同的方法,每种方法都基于不同的假设。
第三步:计算检验统计量。
根据所选的统计方法,我们需要计算出检验统计量的值,然后与临界值进行比较。
第四步:做出结论。
如果检验统计量的值小于临界值,那么我们可以拒绝原假设,说明时间序列是稳定的;如果检验统计量的值大于临界值,那么我们接受原假设,说明时间序列是不稳定的。
常用的单位根检验方法包括ADF检验、PP检验,以及KPSS检验。
ADF检验ADF检验全称为“Augmented Dickey-Fuller test”。
这种检验方法用于检查一个时间序列是否具有单位根,并且可以给出序列是否是平稳序列的信息。
ADF检验的步骤如下:第一步:设定模型。
ADF模型可以通过以下方式表示:$\Delta Y_t=a+bY_{t-1}+\sum_{i=1}^{k-1}\delta\Delta Y_{t-i}+u_t $其中,$\Delta$表示差分运算符,$Y_t$表示时间序列,$k$表示差分的阶数,$u_t$是一个随机变量。
单位根检验详解
第2节 单位根检验由于虚假回归问题的存在,因此检验变量的平稳性是一个必须解决的问题。
在第十二章中介绍用相关图判断时间序列的平稳性。
这一章则给出序列平稳性的严格的统计检验方法,即单位根检验。
单位根检验有很多方法,这里主要介绍DF 和ADF 检验。
序列均值为0则无C ,序列无时间趋势则无trend在介绍单位根检验之前,先认识四种典型的非平稳随机过程。
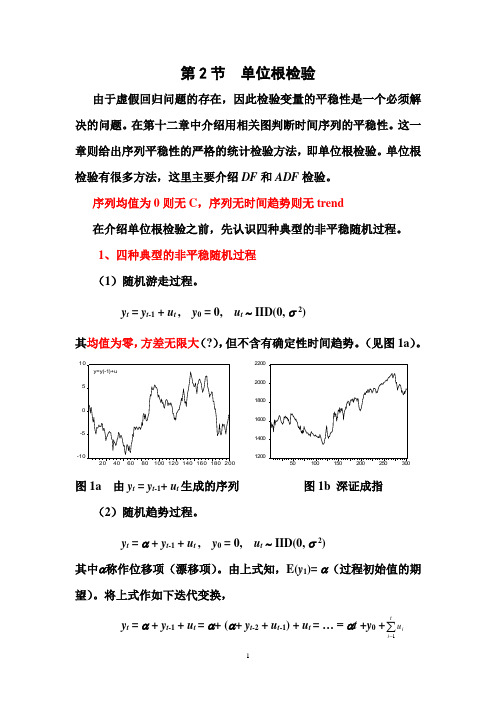
1、四种典型的非平稳随机过程 (1)随机游走过程。
y t = y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) 其均值为零,方差无限大(?),但不含有确定性时间趋势。
(见图1a )。
-10-551020406080100120140160180200y=y(-1)+u12001400160018002000220050100150200250300图1a 由y t = y t -1+ u t 生成的序列 图1b 深证成指(2)随机趋势过程。
y t = α + y t -1 + u t , y 0 = 0, u t ~ IID(0, σ 2) 其中α称作位移项(漂移项)。
由上式知,E(y 1)= α(过程初始值的期望)。
将上式作如下迭代变换,y t = α + y t -1 + u t = α+ (α+ y t -2 + u t -1) + u t = … = αt +y 0 +∑-ti i u 1y t 由确定性时间趋势项αt 和y 0 +∑-t i i u 1组成。
可以把y 0 +∑-ti i u 1看作随机的截距项。
在不存在任何冲击u t 的情况下,截距项为y 0。
而每个冲击u t 都表现为截距的移动。
每个冲击u t 对截距项的影响都是持久的,导致序列的条件均值发生变化,所以称这样的过程为随机趋势过程(stochastic trend process ),或有漂移项的非平稳过程(non-stationary process with drift ),见图2,虽然总趋势不变,但随机游走过程围绕趋势项上下游动。
单位根检验的方法

单位根检验的方法主要有以下几种:
1. ADF检验:即Augmented Dickey-Fuller检验,是对Dickey-Fuller检验的扩展,可以处理含有高阶滞后项的时间序列数据。
它通过在回归模型中加入差分滞后项来控制序列相关的干扰。
2. PP检验:即Phillips-Perron检验,与ADF检验类似,但使用非参数方法来修正序列相关的问题,对小样本性质有一定的改进。
3. KPSS检验:即Kwiatkowski-Phillips-Schmidt-Shin检验,是一种基于平稳序列的检验方法,原假设是序列是平稳的,而备择假设是序列存在单位根。
4. ERS检验:即Elliott-Rothenberg-Stock检验,是一种基于误差修正模型的单位根检验方法,适用于存在长期均衡关系的非平稳时间序列。
5. NP检验:即Nelson-Plosser检验,是一种专门用于检验宏观经济时间序列是否存在单位根的方法。
6. DF-GLS检验:即Dickey-Fuller Generalized Least Squares检验,是一种改进的Dickey-Fuller检验,使用广义最小二乘法来估计模型参数,以提高检验的功效。
7. 霍尔斯检验:即Hall测试,也是一种单位根检验方法,主要用于检测分数整合的存在。
8. 其他检验:还有一些其他的单位根检验方法,如Fisher类型的检验、Maddala-Wu检验等,它们在不同的情况下有各自的适用性和优势。
单位根检验的基本步骤

单位根检验的基本步骤一、单位根检验是啥呢?单位根检验就像是给一组数据做个小检查,看看这组数据是不是平稳的。
这在经济学、统计学里可老重要啦。
你想啊,如果数据不平稳,就像盖房子的地基不稳,那后面基于这些数据做的分析啥的,可能就会出问题。
二、单位根检验的基本步骤1. 选择合适的检验方法常见的有ADF检验(Augmented Dickey - Fuller Test)。
这就好比你要去一个地方,有好几条路可以走,ADF检验就是其中一条比较常用的路。
还有PP检验(Phillips - Perron Test)等其他方法。
选择的时候要根据数据的特点来,要是数据有趋势,那得选能对付这种有趋势数据的检验方法;要是数据有季节性,那也得考虑这个因素。
2. 确定检验的模型形式有三种模型形式呢。
第一种是不带常数项和趋势项的模型,这种适合那种数据看起来就比较简单,没有什么明显的常数特征或者趋势特征的情况。
就像是一个很单纯的数列,没有什么额外的“装饰”。
第二种是带常数项,不带趋势项的模型。
这就好比数列有个基本的“起点”,有个常数在那儿撑着,但没有上升或者下降的趋势。
第三种是带常数项和趋势项的模型。
如果数据看起来像是有个固定的起点,然后还朝着某个方向有趋势地变化,就像股票价格有时候会有上涨或者下跌的趋势,还有个基本的价格底线,那这种模型就比较合适。
3. 设定检验的显著性水平这个显著性水平啊,就像是一个门槛。
一般我们常用的有0.05或者0.01。
这是什么意思呢?就是说如果我们得到的检验统计量比这个门槛对应的临界值更极端,那我们就可以拒绝原假设。
比如说,显著性水平是0.05,就好像是在说,这件事情只有5%的可能性是巧合,要是超过这个巧合的范围,那我们就认为有问题啦。
4. 计算检验统计量根据我们选择的检验方法和模型形式,把数据代入相应的公式里,就像做数学题一样,算出那个检验统计量。
这个过程可不能马虎,要是数据代错了,那结果肯定就不对啦。
adf检验通俗解释

adf检验通俗解释
ADF检验,即单位根检验(Augmented Dickey-Fuller Test),是一种经济学时间序列分析中常用的统计方法。
它用来判断一个时间序列数据是否存在单位根,即是否存在趋势。
通俗地说,单位根检验用来判断时间序列数据的变化趋势是否随机性的,或者说是否存在长期趋势。
如果数据存在长期趋势,就不能用简单的方法进行分析和预测,因为数据变化是有规律的。
而单位根检验可以帮助我们识别数据是否存在长期趋势,从而选择合适的模型来进行进一步分析。
ADF检验的思路是将时间序列数据拆分成趋势项、季节项、残差项等不同部分,然后分别对这些部分进行统计检验。
如果残差项(即剔除了趋势项和季节项后的数据)不存在单位根,那么我们可以认为原始数据也不存在单位根,即没有长期趋势。
通过ADF检验,我们可以得到一个统计量,根据这个统计量的显著性水平,来判断时间序列是否存在单位根。
如果统计量的值小于某个阈值,即p值小于显著性水平,那么我们可以拒绝存在单位根的假设,认为数据不存在长期趋势。
总之,ADF检验是一种用来判断时间序列数据是否存在长期趋势的方法,通过检验序列的残差项是否存在单位根,来判断原始数据是否存在单位根。
单位根检验选取方法

单位根检验选取方法
1. 哎呀,你知道单位根检验选取方法里的那个直观判断法不?就好比你一眼就能看出这个东西好不好一样!比如看股票走势,有时候是不是一眼就能感觉出它的趋势呀,这就有那么点类似直观判断法的意思。
2. 还有那个图形分析法呀,可形象啦!就像你看地图找路一样,在单位根检验里通过图形去分析,能快速找到线索呢!比如说分析气温变化图表,不就能看出个大概趋势啦。
3. 统计量检验法也很重要呢!这就像一个精准的尺子,能衡量出到底合不合格。
就好比挑水果,用一定标准去衡量哪个更好,在单位根检验里就是用统计量去把关呀!
4. 模型比较法咋样?这就如同比赛一样,把几个方法放在一起比一比,看看哪个更厉害!比如在选择旅游线路的时候,对比几条线路看哪个更适合。
5. 经验法则呢,是很实用的哦!就像是老司机的经验,那可都是宝贵的财富。
比如开车遇到某些情况怎么处理,经验法则在单位根检验里也能派上大用场呀。
6. 理论推导法,哇,这个可高深啦!像是解开一个复杂谜题的钥匙。
好比我们解一道很难的数学题,通过理论推导找到答案,单位根检验也常用到这个方法呢。
7. 实际应用验证法,这可太关键啦!就像实践出真知一样。
比如新做的一个东西,实际用一用就知道好不好,单位根检验也要通过实际应用来验证选取方法是否合适。
8. 综合判断法更是牛呀!把各种方法都综合起来考虑,多全面呀!就好像全面评估一个人一样,看好多方面,在单位根检验里综合判断能让结果更准确呢!
我觉得呀,这些单位根检验选取方法都各有特点,要根据具体情况灵活运用,才能得出准确的结果呢!。
stata单位根检验趋势和截距

一、概述Stata作为一款广泛使用的统计软件,常常被用于进行时间序列数据的分析。
在时间序列分析中,我们经常需要进行单位根检验,以确定数据序列是否存在趋势或截距。
通过Stata单位根检验,我们可以对数据序列进行有效的分析和预测,为决策提供重要的参考依据。
二、单位根检验的概念1. 单位根的定义单位根是指在时间序列数据中存在一个根为1的特征方程,也就是说数据序列在一定程度上呈现出随机游走的特性。
2. 单位根检验的目的单位根检验的目的在于确定时间序列数据是否存在趋势或截距,进而对数据进行更准确的建模和预测。
三、Stata中单位根检验的工具1. 时间序列命令Stata中针对时间序列数据的单位根检验主要通过时间序列命令来实现,其中包括adf命令和pperron命令。
2. adf命令adf命令是Stata中用于进行单位根检验的重要工具,其语法为“adf 变量名”,通过这一命令可以对指定变量进行单位根检验,并输出相应的检验结果和统计量。
3. pperron命令四、单位根检验结果的解读1. adf检验结果解读adf检验结果通常包括检验统计量、临界值和p值等信息,需要根据这些信息来判断数据序列是否存在单位根。
2. pperron检验结果解读pperron检验结果类似于adf检验结果,同样需要对检验统计量和p值进行解读,以得出数据序列的单位根检验结论。
五、单位根检验在实际分析中的应用1. 时间序列建模通过单位根检验的结果,可以为时间序列数据的建模提供重要的参考依据,确定合适的模型形式和参数。
2. 趋势预测单位根检验还可以为数据序列的未来走势提供预测和分析,为决策提供支持。
六、结论Stata单位根检验作为时间序列分析中的重要工具,对数据序列的趋势和截距具有重要的作用。
通过对单位根检验工具的熟练使用,可以更准确地分析和预测时间序列数据,为决策提供更可靠的参考依据。
希望本文对Stata单位根检验的概念、工具和应用能够给读者提供一定的帮助和参考。
什么是单位根检验如何进行单位根检验

什么是单位根检验如何进行单位根检验单位根检验是时间序列分析中常用的一种方法,用于判断一个序列是否具有单位根。
本文将介绍单位根检验的概念及其常见方法,并详细说明如何进行单位根检验。
一、单位根检验的概念单位根检验是用来判断一个时间序列数据是否具有单位根的方法。
单位根是指时间序列中的随机游走部分,即序列具有无界的随机性。
如果一个序列是单位根序列,那么它的均值和方差都会随着时间的推移而改变,无法稳定在一个特定的水平上。
单位根检验是为了验证时间序列是否平稳而进行的,平稳序列的均值和方差在时间推移的过程中是固定的,与时间无关。
二、如何进行单位根检验常见的单位根检验方法包括ADF检验(Augmented Dickey-Fuller Test)和KPSS检验(Kwiatkowski–Phillips–Schmidt–Shin Test)。
ADF检验是一种常用的单位根检验方法,它的原假设是序列具有单位根,即非平稳;备择假设是序列是平稳的。
ADF检验会利用时间序列的滞后项来估计单位根系数,进而进行假设检验。
KPSS检验则是另一种常用的单位根检验方法,它的原假设是序列是平稳的;备择假设是序列具有单位根,即非平稳。
KPSS检验会计算序列的累积和,通过比较它与滞后项的关系来判断序列是否具有单位根。
在进行单位根检验时,一般需要确定检验的滞后阶数和选择合适的检验统计量。
通常会根据样本的性质和经验来选择合适的参数。
三、进行单位根检验的步骤下面将以ADF检验为例,介绍进行单位根检验的具体步骤。
1. 收集时间序列数据,确保数据已经按照时间顺序排列。
2. 导入统计软件,比如R或Python等,加载相关的统计函数库。
3. 指定滞后阶数。
根据样本的特点和经验选择合适的滞后阶数,一般建议初始滞后阶数为1或者自动选择。
4. 进行ADF检验,并取得检验统计量的值。
统计软件会输出检验统计量的值,一般为负数,可以与相应的临界值进行比较。
5. 进行假设检验。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
势,一般不会返回某个特定值。大多数宏观 经济流量指标和与人口规模相联系的存量指 标往往都是一阶单整的,如产出和就业人口; 二阶单整序列往往具有一个相对不变的增长 率,如物价指数;三阶及以上单整序列一般 不常见,但并非不存在,如恶性通货膨胀时 期的物价水平可能是三阶单整的。
单位根检验:单位根过程
单位根过程是一种特别常见的非平稳过程。
-3.5778 -2.9256 -2.6005
Augmented Dickey-Fuller Test Equation Dependent Variable: D(DLGIM) Method: Least Squares Date: 06/02/05 Time: 23:14 Sample(adjusted): 1953 1998 Included observations: 46 after adjusting endpoints VariableCoefficient DLGIM(-1) D(DLGIM(-1)) C 0.090999 R-squared Adjusted R-squared S.E. of regression Sum squared resid Log likelihood Durbin-Watson stat Std. Error -0.836358 0.196643 0.032063 0.379331 0.350463 0.175250 1.320646 16.39079 1.917004 t-Statistic Prob. 0.171284 -4.882871 0.129065 1.523594 2.838167 0.0069 Mean dependent var S.D. dependent var Akaike info criterion Schwarz criterion F-statistic Prob(F-statistic) 0.0000 0.1349 0.001161 0.217449 -0.582208 -0.462949 13.14006 0.000035
虚假回归(伪回归) :产生原因
伪回归的产生原因:伪回归现象产生的根本
原因就是序列的非平稳性 当我们引入平稳和非平稳的概念,这些问题 就可以通过一定的方式解决。
虚假回归(伪回归):检验和纠正
伪回归检验
可以利用残差的平稳性检验来判断是否存在 伪回归。如果残差非平稳,则是伪回归。
虚假回归(伪回归):检验和纠正
Eviews提供了如下三种检验形式:
(1)包含常数项 yt yt 1 t (2)包含常数项和线性时间调整项
yt t yt 1 t
(3)无常数项和线性时间调整项
yt yt 1 t
单位根检验:DF和ADF检验
首先观察序列的曲线图。如果常数项显著,
单位根检验:定义
单位根过程是一种特别常见的非平稳过程。
其差分为平稳过程。 一般,如果一个非平稳过程的一阶差分是平 稳的,则称其为一阶单整的,记为I(1);若非 平稳过程经过d次差分以后成为平稳的,则称 其为d阶单整的,记为I(d)。
单位根检验:定义
一阶单整序列一往往具有一个固定的增长趋
单位根检验:DF和ADF检验 假设H : 1。进行与DF相同的检验,临界
0
值表也与DF检验相同,对于的检验则可选用 普通的T分布表或F分布表。由此可见,ADF 检验只是在方程的右边加入了p个Y的滞后项, 从而保证使为白噪声过程。至于p的确定,根 据的显著性检验即可。 Yt 通过单整检验后,说明它至少为一阶单整的,再 对其差分做检验;如果其差分通过了检验,说 明至少为二阶单整的 直到拒绝原假设即不存 在单位根为止。此时即确定了序列的单整阶数。
单位根检验:DF和ADF检验
通过了一阶单整检验后,再建立如下方程: 2 xt ( 1) xt 1 t 进行同样过程的检验。如果通过检验,则说 明序列xt 至少为2阶单整的如果进行直到不 能通过检验为止。此时也就确定了序列xt的单 整阶数。
单位根检验:DF和ADF检验 在DF检验中,由于不能保证方程中的残差为白
伪回归的纠正方法:
1)在回归模型中包含自变量和因变量的一阶 滞后变量,即 yt xt yt 1 xt 1 ut 通过这种方式可以消除伪回归。即当 y 和 x ˆ 不相关,则 和 ˆ 依概率收敛于零。
虚假回归(伪回归):检验和纠正
伪回归的纠正方法:
则选择第一种检验形式;如果存在时间趋势 和常数,则选用第二种检验形式;如果时间 趋势和常数都不显著,就改为无常数项和线 性时间调整项的第三种情形。
单位根检验:DF和ADF检验
运用Eviews软件对y进行ADF检验时,如果滞
后期为0时,即为DF检验。 如何选择p:找AIC和SC最小的p
单位根检验:案例
单位根检验
定义
单位根过程 单位根检验(DF和ADF检验) 单位根检验案例 网上的问题 I(d)过程的检验
单位根检验:定义
平稳性定义:如随机过程{ Yt}满足以下条件,则它 是弱平稳的: (1)E ( yt )与t无关 Var( yt ) 是与t无关的常数 (2) Cov( yt , ys ) 是t-s的函数,但不是t或s的函数 (3)
Banerjee 利用蒙特卡罗模拟得出结论:对于相
虚假回归(伪回归) :定义
虚假回归:两个没有任何逻辑联系的序列进行回 R 2,因为两个序列都与时俱进 归,含有很高的 (具有时间趋势,随时间推移而发生变化)。例 子,考研人数与手机数量。 虚假回归的后果:如果我们不能够判断出来哪些 变量之间是真正存在相关关系的,哪些不是真正 存在关系的,那么当我们用不存在关系的变量进 行相关分析和回归分析时,就会得出错误的结论
单位根检验:单位根过程
单位根过程的性质: 长记忆时间序列和短记忆时间序列:一般地,平稳 过程都是短记忆过程,即序列的当前值不受很早以 前的值的影响或影响很小、以至可以忽略。而单位 根过程则是长记忆过程,即很早以前的值对过程的 当前值仍然具有显著影响,或这种影响不会随时间 的增加而减弱。认识到时间序列的这种长短记忆特 征具有重要意义。如我们观察发现某经济时间序列 为一定形式的单位根过程,则可认为它受到的冲击 具有永久性影响,决策时必须考虑到这一点。
其差分为平稳过程。
单位根检验:单位根过程
单位根过程的性质: 伪回归:如对于某些时间序列,可能它们本 身之间并不相关,但对资料进行计算可以得 到显著的相关系数和回归方程。这种现象称 为伪回归。这是因为回归估计中主要依靠的 是序列的趋势之间的关系,只要两个序列具 有一定的趋势关系,我们就可能会得到显著 的相关系数和回归系数。
单位根检验:定义
AR(1)过程是平稳序列吗?
| 定理:若 | 1,则AR(1)过程是平稳过程。因
为 (1) Eyt
1
2 |h| (2)cov( yt , yt h ) 1 2
2 var( yt ) 1 2
(t , h) |h| (3)
的统计推断都不再成立,因此必须检验被解 释变量和解释变量是不是平稳的。标准的检 验方法是“单位根检验”。
单位根检验:定义
一个随机过程的平稳性取决于其特征方程的
根的值。若所有的根都位于单位圆之外,则 该过程是平稳的。若某个(些)根的值位于单位 圆上或单位圆内,则该过程是非平稳的。若 特征方程的根取值为1,则称其为单位根。对 单位根的检验(即对随机过程单整阶数的检验) 也就是对随机过程平稳性的检验。
ˆ 噪声,所以得到的的估计值不是无偏的。于是 迪基 - 富勒又对由他们提出的这一检验进行了推 广,形成增广的DF检验即ADF检验。 ADF检验为保证方程中的为白噪声,设随机过 程服从AR(p)过程,即 Yt 1Yt 1 2 Yt 2 pYt p t Yt 1 1Yt 1 2 Yt 2 p 1Yt p 1 t
证明过程略
单位根检验:定义
如果 | | 1
,AR(1)过程 {yt}还是平稳过程吗?
为什么? 可以通过数学推导证明; 已知随机步游是非平稳的,当 | | 1 时, AR(1)过程 {yt}为一随机步游过程。
单位根检验:定义
看图识平稳 :
单位根检验:定义
看图识平稳 :
2)对 yt 和 xt 先做一阶差分,从而使得yt 和 xt 变成平稳过程,然后建立模型
yt xt ut
此时能够消除伪回归。即当 y 和 x 不相关, ˆ 则 依概率收敛于零。
虚假回归(伪回归):检验和纠正
伪回归的纠正方法:
3)Cochrane-Orcutt方法(自相关问题) 如果 yt xt ut 其中 ut ut 1 t 则可根据广义差分法,建立模型
ADF Test Statistic
1% Critical Value* 5% Critical Value 10% Critical Value *MacKinnon critical values for rejection of hypothesis of a unit root.
-4.882871
计量经济学
虚假回归(伪回归)
单位根检验 格兰杰因果检验 协整与误差ห้องสมุดไป่ตู้正模型
虚假回归(伪回归)
定义
伪回归产生的原因 伪回归的检验和纠正方法 总结
虚假回归(伪回归):定义
互独立的单整序列 yt xt , u 1, 1, x0 0, y0 0 且 ,进行回归时,t 统计量显示比正常检验临界值水平还高。也就 是在相互独立的序列进行的实际回归中,经常 R2 伴随着高的 ,并且 系数显著。这种现象就 称为为伪回归(虚假回归)现象。
