《简单的逻辑连接词 或且非》
第12讲简单的逻辑联结词(且或非)讲义-高三艺考数学一轮复习
第12讲：简单的逻辑联结词（且或非）【课型】复习课【教学目标】1.了解逻辑联结词【预习清单】【基础知识梳理】1．常用的简单的逻辑联结词有“或”“且”“非”．23【引导清单】考向一：含有逻辑联结词的命题的真假判断例1：（1）命题p ：若sin x ＞sin y ，则x ＞y ；命题q ：x 2＋y 2≥2xy .下列命题为假命题的是( )A ．p 或qB ．p 且qC ．qD ．﹁p（2）记不等式组⎩⎨⎧x ＋y ≥6，2x －y ≥0表示的平面区域为D .命题p ：存在(x ，y )∈D ，2x ＋y ≥9；命题q ：对任意的(x ，y )∈D ，2x ＋y ≤①p 或q ②﹁p 或q ③p 且﹁q ④﹁p 且﹁q这四个命题中，所有真命题的编号是( )A ．①③B ．①②C ．②③D ．③④【解析】（1）取x ＝π3，y ＝5π6，可知命题p 是假命题；由(x －y )2≥0恒成立，可知命题q 是真命题，故﹁p 为真命题，p 或q 是真命题，p 且q 是假命题．（2）在不等式组表示的平面区域D 内取点(7，0)，点(7，0)满足不等式2x ＋y ≥9，所以命题p 正确；点(7，0)不满足不等式2x ＋y ≤12，所以命题q 不正确．所以命题p 或q 和p 且﹁q 正确．故选A.考向二：由命题的真假确定参数的取值范围例2：已知p ：存在x ∈R ，mx 2＋1≤0，q ：任意x ∈R ，x 2＋mx ＋1＞0，若p 且q 为假，p 或q 为真，求实数m 的取值范围．【解析】若p 且q 为假，p 或q 为真，则p ，q 一真一假．当p 真q 假时⎩⎨⎧m ＜0，m ≥2或m ≤－2，所以m ≤－2；当p 假q 真时⎩⎨⎧m ≥0，－2＜m ＜2，所以0≤m ＜2. 所以m 的取值范围是(－∞，－2]∪[0，2)．【训练清单】【变式训练1】设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内．p 2：过空间中任意三点有且仅有一个平面．p 3：若空间两条直线不相交，则这两条直线平行．p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l .则下述命题中所有真命题是________．(填序号)①p 1且p 4 ②p 1且p 2 ③﹁p 2或p 3 ④﹁p 3或﹁p 4【解析】对于p 1，由题意设直线l 1∩l 2＝A ，l 2∩l 3＝B ，l 1∩l 3＝C ，则A ，B ，C三点不共线，所以此三点确定一个平面α，则A ∈α，B ∈α，C ∈α，所以AB ⊂α，BC ⊂α，CA ⊂α，即l 1⊂α，l 2⊂α，l 3⊂α，所以p 1是真命题．以下同方法一．答案：①③④【变式训练2】已知命题p ：关于x 的方程x 2－ax ＋4＝0有实根；命题q ：关于x 的函数y ＝2x 2＋ax ＋4在[3，＋∞)上是增函数．若p 或q 是真命题，p 且q 是假命题，则实数a 的取值范围是________．【解析】命题p 等价于Δ＝a 2－16≥0，即a ≤－4或a ≥4；命题q 等价于－a 4≤3，即a ≥p 或q 是真命题，p 且q 是假命题知，命题p 和q 一真一假．若p 真q 假，则a ＜－12；若p 假q 真，则－4＜aa 的取值范围是(－∞，－12)∪(－4，4)．【巩固清单】1．已知命题p ，q ，则“﹁p 为假命题”是“p 且q 是真命题”的( )条件。
简单的逻辑联接词01或且非
04
“或”、“且”、“非”的组合逻辑
组合逻辑的定义
组合逻辑是数字逻辑电路设计的基础，它研究的是如何将基本的逻辑门电路组合 起来实现特定的逻辑功能。
组合逻辑电路由输入变量、逻辑门和输出变量组成，其功能由输入和输出之间的 逻辑关系决定。
组合逻辑的规则
输入变量的取值可以是0或1，输出变量的取值也相应 为0或1。
电梯的上升和下降控制可以看作 是“或”运算，即只要有人按下 上升按钮或者下降按钮，电梯就 会响应。
80%
电子门锁
电子门锁的开锁和闭锁状态可以 通过“与”运算来控制，只有当 输入正确的密码时，门锁才会打 开。
THANK YOU
感谢聆听
“或”的逻辑规则
逻辑“或”遵循“排除法”原则，即 当两个命题中至少有一个为真时，整 个复合命题为真；反之，如果整个复 合命题为假，则两个命题都为假。
在逻辑“或”的运算中，如果两个命 题有一个是真的，那么“或”运算的 结果就是真。
“或”在日常生活中的例子
02
01
03
例子1
明天下雨或刮风，我们取消户外活动。
P∧Q与Q∧P是等价的。
分配律
P∧(Q∨R)等价于 (P∧Q)∨(P∧R)。
“且”在日常生活中的例子
01
例子1
当我们在描述一个物品时，使用“且”来描述其多个属性。例如，“这
个手机是苹果公司的产品，且具有高分辨率的屏幕。”
02
例子2
在制定计划时，我们使用“且”来描述多个条件同时满足。例如，“我
们计划在星期六下午去电影院看电影，且晚餐选择一家意大利餐厅。”
简单的逻辑联接词01或、且、 非
目
CONTENCT
录
• “或”的逻辑 • “且”的逻辑 • “非”的逻辑 • “或”、“且”、“非”的组合逻
简单的逻辑联结词一或且非
“非”在日常生活中的运用
1 2
决策制定
在决策过程中，人们经常使用“非”来否定某个 选项或观点，以缩小选择范围或排除不合适的方 案。
判断与评价
在评价事物或人时，人们使用“非”来否定某种 不良属性或行为，以强调其正面特质或价值。
3
逻辑推理
在逻辑推理中，“非”常用于否定某个假设或前 提，从而推导出相反的结论或验证某个假设的错 误。
简单的逻辑联结词一 或且非
目录
• “或”的逻辑 • “且”的逻辑 • “非”的逻辑 • 逻辑联结词的综合应用
01
“或”的逻辑
“或”的定义
“或”表示两个命题中至少有一个为 真，则该复合命题为真。
在逻辑中，“或”可以表示为符号 “∨”。
“或”的逻辑性质
交换律
01
P ∨ Q 和 Q ∨ P 是等价的。
“且”的定义
“且”是逻辑联结词中的一种，表示两个命题同时成立。
在逻辑学中，“且”通常用符号“∧”表示，用于连接两个命题。
“且”的逻辑性质
传递性
如果命题A和命题B都为真，那么命题A∧B也为真。
反身性
任何命题P与自身相“且”，结果都为真，即P∧P为真。
交换律
A∧B与B∧A等价。
结合律
A∧(B∧C)等价于(A∧B)∧C。
不确定性推理
逻辑联结词可以用于描述概率和不确定性，例如“P 或 Q”可以表示 P 和 Q 都发生的概率之和。
逻辑联结词在计算机科学中的应用
01
编程语言
02
数据库查询
逻辑联结词在许多编程语言中都有应 用，如 C、Java 和 Python 等。它们 用于控制程序流程，如条件语句和循 环语句。
在数据库查询语言中，逻辑联结词用 于连接多个条件，形成复杂的查询语 句。例如，使用 AND 和 OR 联结多 个查询条件。
知识讲解_逻辑联接词“且”“或”“非”
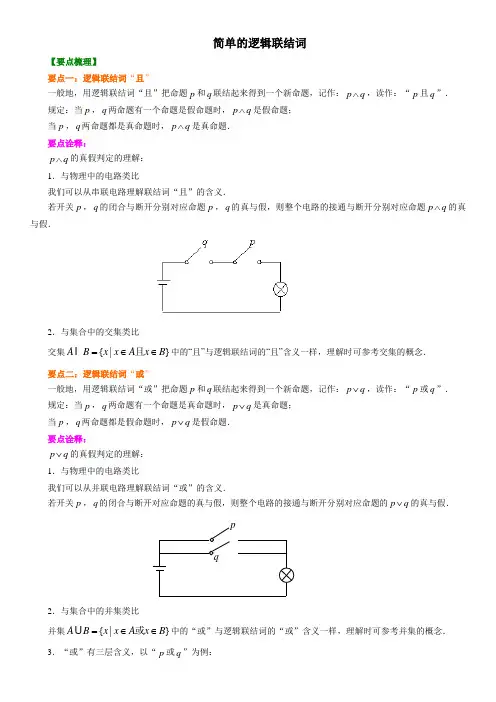
简单的逻辑联结词【要点梳理】要点一：逻辑联结词“且”一般地，用逻辑联结词“且”把命题p 和q 联结起来得到一个新命题，记作：p q ∧，读作：“p 且q ”． 规定：当p ，q 两命题有一个命题是假命题时，p q ∧是假命题； 当p ，q 两命题都是真命题时，p q ∧是真命题． 要点诠释：p q ∧的真假判定的理解：1．与物理中的电路类比我们可以从串联电路理解联结词“且”的含义．若开关p ，q 的闭合与断开分别对应命题p ，q 的真与假，则整个电路的接通与断开分别对应命题p q ∧的真与假．2．与集合中的交集类比交集{|}A B x x A x B =∈∈I 且中的“且”与逻辑联结词的“且”含义一样，理解时可参考交集的概念． 要点二：逻辑联结词“或”一般地，用逻辑联结词“或”把命题p 和q 联结起来得到一个新命题，记作：p q ∨，读作：“p 或q ”． 规定：当p ，q 两命题有一个命题是真命题时，p q ∨是真命题； 当p ，q 两命题都是假命题时，p q ∨是假命题． 要点诠释：p q ∨的真假判定的理解：1．与物理中的电路类比我们可以从并联电路理解联结词“或”的含义．若开关p ，q 的闭合与断开对应命题的真与假，则整个电路的接通与断开分别对应命题的p q ∨的真与假．2．与集合中的并集类比并集{|}A B x x A x B =∈∈U 或中的“或”与逻辑联结词的“或”含义一样，理解时可参考并集的概念． 3．“或”有三层含义，以“p 或q ”为例：qp（1）p 成立且q 不成立； （2）p 不成立但q 成立； （3）p 成立且q 也成立．要点三：逻辑联结词“非”一般地，对一个命题p 全盘否定得到一个新命题，记作：p ⌝，读作：“非p ”或“p 的否定”． 规定：当p 是真命题时，p ⌝必定是假命题； 当p 是假命题时，p ⌝必定是真命题． 要点诠释：1．逻辑联结词中的“非”相当于集合中补集的概念，谈到补集必然要说全集，谈论 “非”时也应该弄清这件事是在一个什么样的范围中研究．2．下面是一些常用词的否定：注意：“一定”的否定不是“一定不”． 3．否命题与命题的否定之间的区别：否命题是对原命题的条件和结论分别做否定后得到的命题（否定二次）；命题的否定是只对原命题的结论做否定（否定一次），即p ⌝．如：命题p ： 若1x =，则(1)(1)0x x -+=． 命题p 的否命题：若1x =/，则(1)(1)0x x -+=/． 命题p 的否定p ⌝：若1x =，则(1)(1)0x x -+=/． 4．“或”、“且”联结的命题的否定形式： “p 或q ”的否定⇔p ⌝且q ⌝； “p 且q ”的否定⇔p ⌝或q ⌝. 要点四：简单命题与复合命题 1. 定义：简单命题：不含逻辑联结词的命题叫简单命题．复合命题：由简单命题与逻辑联结词“或” “且” “非”构成的命题叫做复合命题． 2. 复合命题的构成形式： （1）p 或q ；记作：p q ∨； （2）p 且q ；记作：p q ∧；（3）非p （即命题p 的否定）；记作：p ⌝. 3.复合命题的真假判断要点诠释：1. 当p 、q 同时为假时，“p 或q ”为假，其它情况时为真，可简称为“一真必真”；2. 当p 、q 同时为真时，“p 且q ”为真，其它情况时为假，可简称为“一假必假”；3. “非p ”与p 的真假相反．【典型例题】类型一：复合命题的构成例1．分别指出下列复合命题的形式及构成的简单命题． （1）李明是老师，赵山也是老师； （2）1是合数或质数； （3）他是运动员兼教练员.【思路分析】观察命题结构，判断其中是否还有“或” “且” “非”等联结词或相似含义的联结词，利用“或” “且” “非”的概念对复合命题进行结构分解. 【解析】（1）这个命题是“p 且q ”形式，其中p ：李明是老师，q ：赵山是老师． （2）这个命题是“p 或q ”形式，其中p ：1是合数， q ：1是质数． （3）这个命题是“p 且q ”形式，其中p ：他是运动员，q ：他是教练员．【总结升华】正确理解逻辑联结词“或”、 “且”、 “非”的含义是解题的关键．根据上述各复合命题中出现的逻辑联结词或语句的意义确定复合命题的形式．举一反三：【高清课堂：简单的逻辑联结词395484例1】 【变式1】将下列各组命题用“且”联结组成新命题： （1）p ： 平行四边形的对角线互相平分， q ：平行四边形的对角线相等； （2）p ： 集合A 是A B I 的子集， q ：集合A 是A B U 的子集； （3）p ： 211x +≥， q ：34>． 【答案】（1）p q ∧：平行四边形的对角线互相平分且相等； （2）p q ∧：集合A 是A I B 的子集，且是A U B 的子集； （3）p q ∧：211x +≥，且34>．【变式2】判断下列复合命题的形式，并写出构成其的简单命题 （1）1是奇数或偶数； （2）梯形不是平行四边形； （3）2是偶数也是质数． 【答案】（1）p 或q 的形式，其中p ：1是奇数， q ：1是偶数； （2）非p 的形式， 其中p ：梯形是平行四边形；（3）p 且q 的形式，其中p ：2是偶数， q ：2是质数．例2．判断下列命题中是否含有逻辑联结词“或” “且” “非”，若含有，请指出其中p q 、的基本命题． （1）正方形的对角线垂直相等； （2）2是4和6的约数；（3）不等式2560x x -+>的解为32x x ><或； （4）平行四边形的对角线不一定相等. 【解析】（1）是“p 且q ”形式的命题，其中p ：正方形的对角线互相垂直；q ：正方形的对角线相等． （2）是“p 且q ”形式的命题，其中p ：2是4的约数； q ：2是6的约数． （3）是简单命题，而不是用“或” “且” “非”联结的复合命题； （3）是“非p ”形式的命题，其中p ：平行四边形的对角线一定相等.【总结升华】对于用逻辑联结词“或” “且” “非”联结的新命题的结构特点不能仅从字面上看它是否含有“或”、“且”、“非”等逻辑联结词，而应从命题的结构来看是否用逻辑联结词联结两个命题．举一反三：【变式】指出下列复合命题的结构，写出构成其的简单命题． (1) 菱形的对角线互相垂直平分；（3）6是12或18的约数． 【答案】（1）p 且q 的形式，其中p ：菱形的对角线互相垂直，q ：菱形对角线互相平分；（2）非p 的形式，其中p（3）p 或q 的形式，其中p ：6是12的约数，q ：6是18的约数． 类型二：复合命题真假的判定例3．分别指出下列复合命题的形式及构成它的简单命题，并指出复合命题的真假． （1）8或6都是30的约数； （2）矩形的对角线互相垂直平分； （3）方程210x x ++=无实根.【思路点拨】将复合命题写成“p 或q ”、“p 且q ”、“非p ”的形式，并一一判断p ，q 的真假，再由真值表判断复合命题的真假.【解析】（1）“p 或q ”形式．其中p ：8是30的约数， q ：6是30的约数， ∵p 假q 真，∴该复合命题为真．（2）“p 且q ”形式．其中p ：矩形的对角线互相垂直，q ：矩形的对角线互相平分， ∵p 假q 真，∴该复合命题为假．（3）“非p ”形式．其中p ： 方程210x x ++=有实根，∵p 假，∴该复合命题为真．【总结升华】 先判断各简单命题的真假，再依据复合命题的构成形式写出复合命题，最后判断复合命题的真假．举一反三：【变式1】已知命题p 、q ，试写出p 或q 、p 且q 、非p 的形式的命题并判断真假． （1）p ：平行四边形的一组对边平行， q ：平行四边形的一组对边相等； （2）p ：2{1,3,5,7}∈， q ：2{2,4,6,8}∈； （3）p ：1{12}∈，， q ：{1}⊆{12}，； （4）p ：2{|1}x x ∅=<， q ：∅◊2{|1}x x <； （5）p ：34<， q ：34=． 【答案】（1） p 或q ：平行四边形的一组对边平行或相等（真命题）；p 且q ：平行四边形的一组对边平行且相等（真命题）； 非p ： 平行四边形的一组对边不平行（假命题）．（2） p 或q ：2{1,3,5,7}∈或2{2,4,6,8}∈，即2{1,2,3,4,5,6,7,8}∈（真命题）；p 且q ：2{1,3,5,7}∈且2{2,4,6,8}∈（假命题）； 非p ： 2{1,3,5,7}∈/（真命题）. （3） p 或q ：1{12}∈，或{1}⊆{12}，（真命题）； p 且q ：1{12}∈，且{1}⊆{12}，（真命题）； 非p ： 1{12}∈/，（假命题）. （4） p 或q ：2{|1}x x ∅=<或∅◊2{|1}x x <，即2{|1}x x ∅⊆< （真命题）；p 且q ：2{|1}x x ∅=<且∅◊2{|1}x x <（假命题）； 非p ： 2{|1}x x ∅=</（真命题）.（5） p 或q ：34<或34=，即34≤（真命题）；p 且q ：34<且34=（假命题）； 非p ： 34</，即34≥（假命题）． 【变式2】已知命题p ：33ß； q ：3＞4，则下列判断正确的是（ ） A ．p q ∨为真，p q ∧为真，p ⌝为假 B ．p q ∨为真，p q ∧为假，p ⌝为真 C ．p q ∨为假，p q ∧为假，p ⌝为假 D ．p q ∨为真，p q ∧为假，p ⌝为假 【答案】D【解析】 p ：33ß，是真命题， q ：3＞4是假命题，根据真值表：p q ∨为真，p q ∧为假，p ⌝为假，所以选D ．【变式3】已知命题p ：所有有理数都是实数，命题q ：正数的对数都是负数，则下列命题为真命题的是（ ）A ．()p q ⌝∨B ．p q ∧C ．()()p q ⌝∨⌝D ．()()p q ⌝∧⌝ 【答案】C【变式2】以下判断中正确的是（ ）A ．命题p 是真命题时，命题“p q ∧”一定是真命题B ．命题“p q ∧”为真命题时，命题p 一定是真命题C ．命题“p q ∧”为假命题时，命题p 一定是假命题D ．命题p 是假命题时，命题“p q ∧”不一定是假命题 【答案】B例4. 如果命题“p 且q ”是假命题，“非p ”是真命题，那么 （ ） A .命题p 一定是真命题 B .命题q 一定是真命题 C .命题q 一定是假命题D .命题q 可以是真命题也可以是假命题【思路点拨】由“非p 是真命题”入手，可判断p 的真假性，再由“p 且q 是假命题”可知q 的真假. 【答案】D【解析】∵“非p ”是真命题， ∴p 是假命题，∵“p 且q ”是假命题，∴q 可以是真命题也可以是假命题， ∴选项为D.【总结升华】含逻辑联结词命题的真假情况，利用真值表逆向思考，从而推断出组成命题的真值情况，再进行判断.【变式】如果命题“()p q ⌝∨”为假命题，则（ ） A. p q ，均为假命题 B. p q ，均为真命题C. p q ，中至少有一个为真命题D. p q ，中至多有一个为真命题 【答案】C类型三：命题的否定与否命题例5．写出下列命题的否定和否命题，并判定其真假． （1）p ：在整数范围内，a 、b 都是偶数，则a b +是偶数； （2）p ：若0x ß且0y ß，则0x y +ß． 【解析】(1) p ⌝：在整数范围内，a 、b 都是偶数，则a b +不是偶数（假命题）；p 的否命题是：在整数范围内，若a 、b 不都是偶数，则a b +不是偶数（假命题）； (2) p ⌝：若0x ≥且0y ≥，则0x y +<（假命题）； p 的否命题是：若0x <或0y <，则0x y +<（假命题）． 【总结升华】1. “0x ß且0y ß”的否定是“0x <或0y < ”；“a 、b 都是偶数”的否定为“a 、b 不都是偶数”.2. 命题的否定和否命题是不一样的．举一反三：【变式1】命题 “ABC ∆是直角三角形或等腰三角形”的否定是 ； 【答案】ABC ∆既不是直角三角形，也不是等腰三角形． 【变式2】写出下列命题的否定和否命题，并判定其真假． （1）p ：若220x y +=，则x ，y 全为零； （2）p ：若3x =且5y =，则8x y +=． 【答案】(1) p 的否定：若220x y +=，则x ，y 不全为零 （假命题）；p 的否命题：若220x y +=/，则x ，y 不全为零 （真命题）； (2) p 的否定：若3x =且5y =，则8x y +=/ （假命题）； p 的否命题：若3x =/或5y =/，则8x y +=/ （假命题）． 【变式3】 “220x y +=/”是指 （填出符合条件的所有选项） A ．0x ≠且0y ≠ B ．0x ≠或0y ≠C ．x ，y 至少有一个不是0D ．x ，y 都不是0E ．x ，y 不都是0 【答案】B 、C 、E【解析】220x y +=/是指x ，y 不同时为零，即x ，y 至少有一个不是0，亦即x ，y 不都是0，0x ≠或0y ≠． 类型四：复合命题的应用例6．已知命题2560p x x +：－ß；命题04q x <<：．若p 是真命题，q 是假命题，求实数x 的取值范围．【解析】 由2560x x +－ß得x ≥3或x ≤2． ∵命题q 为假，∴x ≤0或x ≥4．则{x |x ≥3或x ≤2}∩{x |x ≤0或x ≥4}＝{x |x ≤0或x ≥4}． ∴满足条件的实数x 的范围为(－∞，0]∪[4，＋∞)．【总结升华】解答这类问题，应先由每个简单命题为真，确定参数的取值范围，再由复合命题的真值，得参数所满足的条件，进而确定参数的取值范围．举一反三：【变式】已知命题p ：方程210x +mx+＝有两个不等的负实数根；命题q ：方程244(2)10x +m x+－＝无实数根．若“p 或q ”为真命题，“p ⌝”为真命题，求m 的取值范围．【解析】∵方程210x +mx+＝有两个不等的负实数根， ∴2m >， ∵方程244(2)10x +m x+－＝无实数根，∴13m << 由条件可知，p 假q 真，。
简单的逻辑联结词-或且非ppt课件
如何确定命题“p∧q”的真假性呢？ 规定：
当p,q都是真命题时, “p∧q”是真命题; 当p,q两个命题中有一个是假命题时， “ p∧q”是假命题. 简记为：有假则假.
例1 将下列命题用“且”联结成新命题,并 判断它们的真假: (1)p:平行四边形的对角线互相平分,
q:平行四边形的对角线相等;
思考: 如果p且q为真命题,那么p或q一定为真命题吗?
反之,如果p或q为真命题,那么p且q一定是真命题吗?
p
q
p且q
p或q
真
真
真
真
真
假
假
真
假
真
假
真
假
假
假
假
探究点3 联结词“非”
下列两个命题间有什么关系？ （1）35能被5整除; （2）35不能被5整除.
答案：命题(2)是命题(1)的否定.
【提升总结】
思考：写出命题p: “正方形的四条边相等”
的否定与它的否命题.
命题┓p： 正方形的四条边不相等.
若P一的个否四命边题形：不是正方形，则它的四条边不相等.
命题的否定与否命题的区别
• （1）原命题“若P则q” 的形式，它的非命 题（即命题的否定）“若p，则q”；而它 的否命题为 “若┓p，则┓q”.
• （2）命题的否定（非）的真假性与原命题 相反；而否命题的真假性与原命题无关.
例2 用逻辑联结词“且”改写下列命题,并判断 它们的真假： (1)1既是奇数,又是质数; (2)2和3都是质数.
解：(1)改写为:1是奇数且1是质数.由于“1是质数” 是假命题,所以该命题为假命题. (2)改写为:2是质数且3是质数.因为“2是质数”与 “3是质数”都是真命题,所以该命题为真命题.
简单的逻辑联结词(一)或且非
A）.U指出下列复合命题的形式及构成它的简单命题：的倍数，也是）李强是篮球运动员或跳高运动员；）平行线不相交七、课后练习1．命题“方程x 2＝2的解是x ＝±2是( )A ．简单命题B ．含“或”的复合命题C ．含“且”的复合命题D ．含“非”的复合命题 2．用“或”“且”“非”填空，使命题成为真命题： （1）x ∈A ∪B ，则x ∈A__________x ∈B ； （2）x ∈A ∩B ，则x ∈A__________x ∈B ；（3）a 、b ∈R ，a ＞0__________b ＞0，则ab ＞0． 3．把下列写法改写成复合命题“p 或q ”“p 且q ”或“非p ”的形式： （1）（a －2）（a+2）=0； （2）⎩⎨⎧==21y x ； （3）a ＞b ≥0．4．已知命题p ：a ∈A ，q ：a ∈B ，试写出命题“p 或q ”“p 且q ”“┐p ”的形式． 5．用否定形式填空：(1)a ＞0或b ≤0； (2)三条直线两两相交(3)A 是B 的子集.___________________ (4)a ，b 都是正数.___________ (5)x 是自然数.___________________(在Z 内考虑)6．在一次模拟打飞机的游戏中，小李接连射击了两次，设命题p １是“第一次射击中飞机”，命题p ２是“第二次射击中飞机”试用p １、p ２以及逻辑联结词或、且、非(∨，∧，┐)表示下列命题：命题S ：两次都击中飞机； 命题r ：两次都没击中飞机； 命题t ：恰有一次击中了飞机； 命题u ：至少有一次击中了飞机. 八、参考答案： 1．B 2．（1）或 （2）且 （3）且 3．（1）p ：a －2=0或q ：a+2=0； （2）p ：x=1且q: y=2 （3）p ：a ＞b 且q ：b ≥0 4．命题“p 或q ”：a ∈A 或a ∈B ．“p 且q ”：a ∈A 且a ∈B ．“┐p ”：a ∉A 5．(1)a ≤0且b ＞0(2)三条直线中至少有两条不相交 (3)A 不是B 的子集 (4)a ，b 不都是正数 (5)x 是负整数．6．（1）p q ∧ （2）p q ⌝∧⌝（3）()()p q p q ∧⌝∨⌝∧（4）()p q ⌝⌝∧⌝。
121逻辑联结词“非”“且”和“或”(课件)
（1）我给傻子让路（2）你批评家是傻子（3）我给你 让路。
２
１.２.１逻辑联结词
“非”、“且”、“或”
问１.下列语句哪些是命题，哪些不是命 题？并说明理由。
问２.下列语句是命题吗？如果是命题，则与前 面的命题(1)(2)(3)在结构上有什么区别？
（8） 0.5是非整数 （9） 菱形的对角线互相垂直且平分 （10）10可以被2或5整除
(1) 0.5是整数
(2) 3是12的约数
“非”、“且”、“或”这些词就叫做逻辑
联结词。
(3)12>5
１.联结词＂非＂（not ) 设p是一个命题，联结词＂非＂是对命
是假p命题q.
Pq 真真 真假 假真 假假
pq
真 假 假 假
“全真为真，有假即假”
例２.根据下列命题中的p，q ，写出命题p∧q.
（１）p：矩形的对角线互相平分， 真 q：矩形的对角线互相垂直； 假
（２）p： 2 是无理数， 真 解： q： 2 大于1 真
(1) p q : 矩形的对角线互相垂直且平分 假 (2) p q : 2 是大于1的无理数。 真
3．联结词“或” 一般地，用(o联r) 结词“或”把命题p和命题q 联结起来，就得到一个新命题，记作p∨q ， 读作“p或q ”.
例如：p: ６是２的倍数； q：６是３的倍数。 则p∨q ：６是２或３的倍数。
例３.根据下列命题的p，q，写出命题“ p∨q”。
(1) p：５是集合{２，３，４}中思的考元：素如，何判 q：３是集合{２，３，４}中的定元p∨素q；命题
1.3逻辑联结词且、或、非1
新课引入:
在 数 学 中常 常 要使 用 逻辑 联 结词 “且”、“或”、“非”，它们与日常 生活中这些词语所表达的含义和用法是 不尽相同的，下面我们就分别介绍数学 中使用联结词 “且”、“或”、“非” 联结命题时的含义与用法。 为了叙述简便，今后常用小写字母p， q，r，s，…表示命题。
A
A∩B
B
问题探究:
命题p∧q的真假如何确定?
p q 如图,在串联电路中,若开关 p, q的闭合与断开分别对应 命题p, q的真假,则整个电路 的接通与断开分别对应命题 p∧q的真与假.问整个电路 接通的充要条件是什么? 结论:开关p, q都闭合是整个电路接通的充要 条件.即, p∧q为真的充要条件是p为真同时q 为真.
不都是 至多有n 个 任意 两个
某个
某些
至少有n 某两个 ＋1个
例.已知p:|x2-x|≥6,q:x∈Z.p且q与非q都是 假命题,求x的值
解：非q假 q真
2
又p且q假
p假
x 1,0,1,2
2 |x x| 6 6 x x 6 即 x Z x Z 2 x 3 x Z
1.3 简单的逻辑联结词(二)
思考：
下列两个命题间有什么关系？ （1）35能被5整除； （2）35不能被5整除.
可以看到，命题(2)是命题(1)的否定.
一般地，对一个命题p全盘否定，就得 到一个新命题，记作¬ p，读作“非p”或“p的 否定”
如果p：集合A，则¬p为集合 C A
U
C
A U
A
U
p 真 假
非p 假 真
一般地，我们规定: 若p是真命题，则¬p必是假命题，若p 是假命题，则¬p必是真命题。
逻辑连接词且或非
命题的否定须注意的几个方面:
(1)“≥”的意义是“＞或＝”． (2)“非”命题对常见的几个正面词语的否定.
或 = > 是 都是 至多 至少 任 所 有一 有一 意 有 个 个 的的
且 ≠ ≤ 不 不都 至少 没有 某 某 是 是 有两 一个 个 些 个
例4已知命题p：能被5整除的整数的个位数 一定为5；命题q：能被5整除的整数的个位 数一定为0，则p∨q:_______________
注：逻辑联结词“且”与日常用语中的“并且”、“又”、 “和”相当；表明前后两者同时兼有，同时满足 .
例1 将下列命题用“且”联结成新命题并判断它们的真假：
1：命题p:函数 y x 是奇函数；
真
命题q:函数 y x 在定义域内是增函数； 真
命题p∧q: 函数 y=x是奇函数且在定义域是 增函数。
下列三个命题间有什么关系? (1)35能被5整除； (2)35不能被5整除.
全（特） 称命题 的否定
是怎样
一般地,对一个命题p加以否定,就得到一的？
个新命题,称为p的非命题记作 p
读作“非p”或“p的否定”
p
p
若p是真命题,则¬p必是假命题;
若p是假命题,则¬p必是真命题.
例5 写出下列命题的否定，并判断它们的真假：
假
命题p∨q: 3>2或3<2。
假
命题p∨q的真假判断方法：
一般地，当p，q两个命题中只要有 一个命 题是真命题时,p∨q就是 命真题；当p，q两 个命题都是假命题时，p∨q是 命假题.
有真即真，全假为假
p
q p∨q
真真真
p q
真假真
假真真
假假假
例3：判断下列命题的真假： （1）2≤2； （2）集合A是A∩B的子集且是A∪B的子集； （3）周长相等的两个三角形全等或面积相等的两个三 角形全等.
简单的逻辑联结词或(or)且(and)非(not)
简单的逻辑联结词或(or)且(and)非(not) 教学目标1.理解逻辑联结词“且”“或”“非”的含义.(重点)2.会判断命题“p∧q”“p∨q”“﹁p”的真假.(难点)3.掌握命题的否定与否命题的区别.(易混点)教材整理1 “且”“或”“非”的含义阅读教材P14第1段～第6段，P15“思考”～第3段，P16“思考”～第2段，完成下列问题.1..用联结词“且”把命题p和命题q联结起来，就得到一个新命题，记作p∧q，读作“p且q”.2.用联结词“或”把命题p和命题q联结起来，就得到一个新命题，记作p∨q，读作“p或q”.3.对一个命题p全盘否定，就得到一个新命题，记作﹁p，读作“非p”或“p的否定”.课堂练习1.命题：“菱形的对角线互相垂直平分”，使用的逻辑联结词的情况是()A.没有使用逻辑联结词B.使用了逻辑联结词“且”C.使用了逻辑联结词“或”D.使用了逻辑联结词“非”【解析】菱形的对角线互相垂直且互相平分.∴使用逻辑联结词“且”.【答案】 B2.若p：正数的平方大于0，q：负数的平方大于0，则p∨q：________.(用文字语言表述)【答案】正数或负数的平方大于0教材整理2 含有逻辑联结词的命题的真假判断阅读教材P14第7,8段，P15最后两行，P17第3,4段，完成下列问题.课堂练习1.已知命题p：5≤5，q：5＞6，则下列说法正确的是()A.p∧q为真，p∨q为真，﹁p为真B.p∧q为假，p∨q为假，﹁p为假C.p∧q为假，p∨q为真，﹁p为假D.p∧q为真，p∨q为真，﹁p为假【解析】易知p为真命题，q为假命题，由真值表可得：p∧q为假，p∨q为真，﹁p为假.【答案】 C2.若命题p：常数列是等差数列，则﹁p：________.【解析】只否定命题的结论：常数列不是等差数列.【答案】常数列不是等差数列例题分析(1)用适当的逻辑联结词填空(填“且”“或”“非”)：①若a2＋b2＝0，则a＝0________b＝0；②若ab＝0，则a＝0________b＝0；③平行四边形的一组对边平行________相等.【解析】①若a2＋b2＝0，则a＝0且b＝0，故填且.②若ab＝0，则a＝0或b＝0，故填或.③平行四边形的一组对边平行且相等，故填且.【答案】①且②或③且(2)将下列命题写成“p∧q”“p∨q”和“﹁p”的形式：①p：6是自然数，q：6是偶数；②p：∅⊆{0}，q：∅＝{0}；③p：甲是运动员，q：甲是教练员.【解】①p∧q：6是自然数且6是偶数.p∨q：6是自然数或6是偶数. ﹁p：6不是自然数.②p∧q：∅⊆{0}且∅＝{0}.p∨q：∅⊆{0}或∅＝{0}. ﹁p：∅⃘{0}.③p∧q：甲是运动员且甲是教练员.p∨q：甲是运动员或甲是教练员.﹁p：甲不是运动员.小结1.判断一个命题的构成形式时，不能仅从命题的字面上找逻辑联结词，而应当从命题的结构特征进行分析判断.2.用逻辑联结词构造新命题的两个步骤3.常见词语的否定形式：[再练一题]1.(1)判断下列命题的形式(从“p∨q”“p∧q”和“﹁p”中选填一种)：①π不是整数：______；②6≤8：______；③2是偶数且2是素数：_______.(2)分别写出由下列命题构成的“p∨q”“p∧q”“﹁p”形式的命题：①p：方程x2＋2x＋1＝0有两个相等的实数根，q：方程x2＋2x＋1＝0的两根的绝对值相等；②p：三角形的外角等于与它不相邻的两个内角的和，q：三角形的外角大于与它不相邻的任何一个内角.【解析】(1)①﹁p②p∨q③p∧q(2)①“p∨q”：方程x2＋2x＋1＝0有两个相等的实数根或两根的绝对值相等；“p∧q”：方程x2＋2x＋1＝0有两个相等的实数根且两根的绝对值相等；“﹁p”：方程x2＋2x＋1＝0没有两个相等的实数根.②“p∨q”：三角形的外角等于与它不相邻的两个内角的和或大于与它不相邻的任何一个内角；“p∧q”：三角形的外角等于与它不相邻的两个内角的和且大于与它不相邻的任何一个内角；“﹁p”：三角形的外角不等于与它不相邻的两个内角的和.指出下列命题的真假：(1)命题：“不等式|x＋2|≤0没有实数解”；(2)命题：“－1是偶数或奇数”；(3)命题：“2属于集合Q，也属于集合R”.【精彩点拨】本题主要考查判断复合命题的真假，关键是搞清每个简单命题的构成形式.【自主解答】(1)此命题是“﹁p”的形式，其中p：不等式|x＋2|≤0有实数解.∵x＝－2是该不等式的一个解，∴命题p为真命题，即﹁p为假命题，故原命题为假命题.(2)此命题是“p或q”的形式，其中p：－1是偶数，q：－1是奇数. ∵命题p为假命题，命题q为真命题，∴“p∨q”为真命题，故原命题为真命题.(3)此命题为“p∧q”的形式，其中p：2∈Q，q：2∈R.∵命题p为假命题，命题q为真命题.∴命题“p∧q”为假命题，故原命题为假命题.小结判断含逻辑联结词的命题的真假时，首先确定该命题的构成，再确定其中简单命题的真假，最后由真值表进行判断.[再练一题]2.分别写出由下列各组命题构成的“p∧q”“p∨q”“﹁p”形式的命题，并判断其真假.(1)p ：等腰梯形的对角线相等，q ：等腰梯形的对角线互相平分； (2)p ：函数y ＝x 2－2x ＋2没有零点，q ：不等式x 2－2x ＋1>0恒成立. 【解】 (1)p ∧q ：等腰梯形的对角线相等且互相平分，假命题. p ∨q ：等腰梯形的对角线相等或互相平分，真命题. ﹁p ：等腰梯形的对角线不相等，假命题.(2)p ∧q ：函数y ＝x 2－2x ＋2没有零点且不等式x 2－2x ＋1>0恒成立，假命题. p ∨q ：函数y ＝x 2－2x ＋2没有零点或不等式x 2－2x ＋1>0恒成立，真命题. ﹁p ：函数y ＝x 2－2x ＋2有零点，假命题.探究 对涉及命题的真假且含参数的问题，参数范围怎样确定？【提示】 已知命题p ∧q 、p ∨q 、﹁p 的真假，可以通过真值表判断命题p 、q 的真假，然后将命题间的关系转化为集合间的关系，利用解不等式求参数的范围，要注意分各种情况进行讨论.已知命题p ：方程x 2＋2ax ＋1＝0有两个大于－1的实数根，命题q ：关于x 的不等式ax 2－ax ＋1>0的解集为R ，若“p 或q ”与“﹁q ”同时为真命题，求实数a 的取值范围. 【精彩点拨】分别解出p ，q 中a 的范围→由条件得出p ，q 的真假→求出a 的取值范围 【自主解答】 命题p ：方程x 2＋2ax ＋1＝0有两个大于－1的实数根，等价于⎩⎨⎧Δ＝4a 2－4≥0，x 1＋x 2>－2，(x 1＋1)(x 2＋1)>0⇔⎩⎨⎧a 2－1≥0，－2a >－2，2－2a >0，解得a ≤－1.命题q ：关于x 的不等式ax 2－ax ＋1>0的解集为R ，等价于a ＝0或⎩⎨⎧a >0，Δ<0，由于⎩⎨⎧ a >0，Δ<0⇔⎩⎨⎧a >0，a 2－4a <0，解得0<a <4，∴0≤a <4.因为“p 或q ”与“﹁q ”同时为真命题，即p 真且q 假，所以⎩⎨⎧a ≤－1，a <0或a ≥4，解得a ≤－1.故实数a 的取值范围是(－∞，－1].小结应用逻辑联结词求参数范围的四个步骤1.分别求出命题p，q为真时对应的参数集合A，B.2.由“p且q”“p或q”的真假讨论p，q的真假.3.由p，q的真假转化为相应的集合的运算.4.求解不等式或不等式组得到参数的取值范围.[再练一题]3.已知命题p：方程2x2＋ax－a2＝0在[－1,1]上有解；命题q：只有一个实数x0满足不等式x20＋2ax0＋2a≤0.若命题“p或q”是假命题，求a的取值范围. 【解】由2x2＋ax－a2＝0，得(2x－a)(x＋a)＝0，∴x＝a2或x＝－a，∴当命题p为真命题时，⎪⎪⎪⎪⎪⎪a2≤1或|－a|≤1，∴|a|≤2. 又“只有一个实数x0满足不等式x20＋2ax0＋2a≤0”，即抛物线y＝x2＋2ax＋2a与x轴只有一个交点，∴Δ＝4a2－8a＝0，∴a＝0或a＝2，∴当命题q为真命题时，a＝0或a＝2，∴命题“p或q”为真命题时，|a|≤2.∵命题“p或q”为假命题，∴a>2或a<－2.即a的取值范围为(－∞，－2)∪(2，＋∞).1.已知命题p：3≥3，q：3＞4，则下列判断正确的是()A.p∨q为真，p∧q为真，﹁p为假B.p∨q为真，p∧q为假，﹁p为真C.p∨q为假，p∧q为假，﹁p为假D.p∨q为真，p∧q为假，﹁p为假【解析】p为真，q为假，故选D. 【答案】 D2.已知命题p：对任意x∈R，总有2x>0；q：“x>1”是“x>2”的充分不必要条件.则下列命题为真命题的是()A.p∧qB.﹁p∧﹁qC.﹁p∧qD.p∧﹁q【解析】因为指数函数的值域为(0，＋∞)，所以对任意x∈R，y＝2x>0恒成立，故p为真命题；因为当x>1时，x>2不一定成立，反之当x>2时，一定有x>1成立，故“x>1”是“x>2”的必要不充分条件，故q为假命题，则p∧q、﹁p 为假命题，﹁q为真命题，﹁p∧﹁q、﹁p∧q为假命题，p∧﹁q为真命题，故选D.【答案】 D3.命题“若x＞0，则x2＞0”的否定是________.【答案】若x＞0，则x2≤04.命题p：x＝π是y＝|sin x|的一条对称轴；q：2π是y＝|sin x|的最小正周期.下列命题：①p∨q；②p∧q；③﹁p；④﹁q.其中真命题的序号是________.【解析】∵π是y＝|sin x|的最小正周期，∴q为假.又∵p为真，∴p∨q为真，p∧q为假，﹁p为假，﹁q为真.【答案】①④5.判断下列命题的真假：(1)函数y＝cos x是周期函数并且是单调函数；(2)x＝2或x＝－2是方程x2－4＝0的解.【解】(1)由p：“函数y＝cos x是周期函数”，q：“函数y＝cos x是单调函数”，用联结词“且”联结后构成命题p∧q.因为p是真命题，q是假命题，所以p∧q是假命题.(2)由p：“x＝2是方程x2－4＝0的解”，q：“x＝－2是方程x2－4＝0的解”，用“或”联结后构成命题p∨q.因为p，q都是真命题，所以p∨q是真命题.。
简单的逻辑连接词
简单的逻辑连接词1，且定义：一般地，用逻辑连接词“且”把命题ｐ和命题ｑ联接起来，就得到一个新的命题，记作ｐ∧ｑ，读着“p且q”命题p∧q的真假：命题p 命题q p∧q (p且q)真真真真假假假真假假假假总结：一假则假，全真则真。
2．或定义：一般地，用联接词“或”把命题p和命题q联接起来就得到一个新命题，记着“p∨q”,读作“p或q”.命题p或q的真假：命题p 命题q p∨q (p或q)真真真真假真假真真假假假总结：有真则真，全假则假。
3.“非”定义：一般地，对一个命题p全盘否定，就得到一个新命题，记着﹁p,读着“非p”,“或p的否定”。
命题﹁p的真假：命题p ﹁p (非p)真假假真总结：一真一假。
典型例题例1：将下列各组命题用“且”联接成新命题，并判断真假。
（1）p:π是无理数； q: π小于4；（2）p：5是17的约数； q: 5是15的约数；（3）p: 梯形的对角线相等； q: 梯形的对角线互相平分；（4）p: 2x2+3＞x-5； q: 2x2+3＜x-5；例2：将下列各组命题用“或”联接成新命题，并判断真假。
（1） p: 3＞4, q: 3＜4；（2） p: 正数的平方大于0； q；负数的平方大于0；（3） p: π是整数； q: π是分数。
例3：写出下列命题的否定，并判断它们的真假；（1）p: y=tan x是奇函数，（2）p: π=3.1415；（3）p: 2,3都是8的约数；（4）p: 一元二次方程至多有两个解。
例4：指出下列命题的形式和结构（1）45是3和15的倍数；（2）4是合数或偶数；（3）方程x2+1=0没有有理根。
例5：写出下列命题的否定及否命题（1）面积相等三角形是全等三角形；（2）若m2+n2+x2+y2=0,则实数m,n,x,y全为零；（3）若xy=0,则x=0,y=0.例6：已知：p:方程x2+mx+1=0有两个不等的负实数根；q:方程4x2+4(m-2)x+1=0无实数根，若p∨q为真，p∧q为假，求m的取值范围。
13简单逻辑连接词或且非(优质课)精品PPT课件
★★ 或 (or)
1.问题1： 下列命题中，命题 间有什么关系？
思考： (1)27是7的倍数; (2)27是9的倍数; (3)27是7的倍数或是9的倍数.
命题(3)是由命题(1)(2)使用联结词“或”联结 得到的新命题.
一般地，用联结词“或”把命题p和命题q联结起 来，就得到一个新命题，记作p∨q，读作“p或 q”.
含有逻辑联结词“且”、“或”、“非”的命题称为复合命题
1.命题“方程x2=1的解是x=±1”,使用逻辑联结词的情况
是 (B) A.没有使用逻辑联结词
B.使用了逻辑联结词“或”
C.使用了逻辑联结词“且” D.使用了逻辑联结词“非”
2.已知p:2+2=5,q:3>2,则下列判断中,错误的是 ( C ) A.p或q为真,非q为假 B.p且q为假,非p为真 C.p且q为假,非p为假 D.p且q为假,p或q为真
1.3简单逻辑连接词
一个明智的人总是抓住机遇， 把它变成美好的未来。
同学们：加油！！！
目标解读
知识与技能：了解逻辑连接词“或”“且”“
非”的含义，会用“且”“或”连接两个命题 ，能判断含有逻辑连接词“且”“或”命题的 真假。
过程与方法：通过实例，领悟逻辑连接词
“或”“且”“非”构成的命题形式，体会由 特殊到一般的思想方法。
且 ≠ ≤ 不 不都 至少 没有 某 某 是 是 有两 一个 个 些 个
写在最后
经常不断地学习,你就什么都知道。你知道得越多,你就越有力量 Study Constantly, And You Will Know Everything. The More
You Know, The More Powerful You Will Be
1.2.1 逻辑联结词“非”、“且”、“或”
“”与“”类似
例如：p：a>3 q：a<5
p q：a 3且a 5, 即：3 a 5
q
p
p q的真值表如下：
p q p q
真真真
类似于串联电路， 真 假 假 一假“且”即假
当且仅当开关p与 开关q都闭合时，
假
真
假
灯才会亮
假假假
例2：书本P15（详见书本）
补例 用逻辑连结词"且"改写下列命题,并判断 它们的真假:
1.2 简单的逻辑联结词
1.2.1 逻辑联结词“非”、“且”、“或”
联结词“非”
我们学习了命题的否命题，知道“若p则q”的否命题为 “若﹁p则﹁q”,其中“﹁p”是p的否定“﹁q”是q的否定。
“非” 否定
﹁p:排除p以外的所有事实
（概率中，即为求对立事件）
例如：p:a是大于5的实数,则﹁p：a是不大于5的实数
真
(4)﹁p：方程至少有三个解
假
(5)﹁p：小王和小李不都是一中的学生 假
即：小王或小李不是一中的学生
常用否定词语如下：
正面词语 = >
否定词语
是
不是
全是不全是至多有源自个至少有两个至少有一个
一个也没有
至多有n个
至少有n+1个
至少有k个
至多有k-1个
任意（每一个） 存在（某一个）
所有
存在某一些
a且b
11既是奇数,又是素数; 22和3都是素数.
解 1命题"1既是奇数,也是素数"可以改写
为"1是奇数且1是素数"因为"1是素数"是假命 题, 所以这个命题是假命题.
2命题" 2和3都是素数"可以改写为"2是素数
简单的逻辑联结词(第一课时)“且”“或”“非” 课件
正面词语 否定词语 正面词语
等于 不等于
都是
大于(>) 不大于
(≤) 任意的
是 不是 至多有一个
否定词语 不都是 某一个 至少有两个
正面词语 否定词语
至少有一个 一个也没有
ቤተ መጻሕፍቲ ባይዱ
3.判断含有逻辑联结词“或”、“且”、“非”的命题 的真假
(1)弄清构成命题的p，q的真假； (2)弄清结构形式； (3)用真值表判别命题的真假．
题型二 判断命题的真假 例2 分别指出下列命题的形式及构成它的命题，并判 断真假： (1)相似三角形周长相等或对应角相等； (2)9的算术平方根不是－3； (3)垂直于弦的直径平分这条弦，并且平分弦所对的两段 弧．
分析 根据组成上述各命题的语句中所出现的逻辑联结 词，并用真值表判断真假．
解 (1)这个命题是 p∨q 的形式，其中 p：相似三角形周 长相等；q：相似三角形对应角相等，因为 p 假 q 真，所以 p ∨q 为真．
答案 1．“且”、“或”、“非” 2．真 真 假 假 真 假 假 真 真 假 假 真
1.对逻辑联结词“或”的理解 (1)“或”与日常生活用语中的“或”意义不同．日常生 活用语中的“或”带有“不可兼有”的意思，如工作或休 息，而逻辑联结词“或”含有“同时兼有”的意思，如x<－ 1，或x>2.
(2)“或”与集合A∪B有关系，A∪B＝{x|x∈A，或x∈ B}．集合的并集是用“或”来定义的．
规律技巧 一个命题“若 p，则 q”的否定是：“若 p， 则﹁q”；否命题为：“若﹁p，则﹁q”.
4．命题的否定与否命题 (1)一个命题的否定(非)只否定结论，而一个命题的否命 题是对条件和结论都否定．
如：命题 p：空集是集合 A 的子集．綈 p：空集不是集合 A 的子集．否命题：若集合不是空集，则它不是集合 A 的子集．因 此，一个命题的否定与它的否命题是有区别的．
简单逻辑连接词或、且、非
目录
• “或”的逻辑 • “且”的逻辑 • “非”的逻辑 • “或”、“且”、“非”的组合逻辑 • 逻辑连接词在计算机科学中的应用
01 “或”的逻辑
“或”的定义
01
“或”表示两个命题中至少有一 个为真，则该复合命题为真。
02ቤተ መጻሕፍቲ ባይዱ
“或”可以用于连接两个命题， 表示它们之间的逻辑关系。
THANKS FOR WATCHING
感谢您的观看
且（AND）
逻辑且在人工智能中用于表示多个条件必须同时满足时，才触发某个事件或行为。例如， 在自然语言处理中，可以使用逻辑且来构建规则，要求多个语法规则同时满足时，才能识 别出某个短语或句子。
非（NOT）
逻辑非在人工智能中用于否定某个条件或规则。例如，在知识表示中，可以使用逻辑非来 否定某个事实或规则。
例如，“明天去游泳且看电影。”表 示两个活动同时进行。
03 “非”的逻辑
“非”的定义
“非”是逻辑中的基本否定词，表示 对某一命题的否定。
“非”通常用符号“¬”表示，置于 命题之前，表示该命题的否定。
“非”的逻辑性质
01
“非”具有传递性
如果命题A的否定是B，命题B的 否定是C，那么命题A和C是等价 的。
条件判断
在制定条件语句时，“或”用于表示满足任一条件即可。
02 “且”的逻辑
“且”的定义
1
“且”逻辑连接词表示两个或多个命题同时成立 。
2
在逻辑学中，“且”通常用符号“∧”表示。
3
在自然语言中，“且”通常用“和”或“并且” 来表示。
“且”的逻辑性质
01
02
03
结合律
p∧(q∧r)=(p∧q)∧r，即 “且”具有结合律，可以 任意组合。
高中数学选修2-1课件1.3简单的逻辑联结词
3.已知 c>0,设 p:函数 y cx 在 R 上递减; q:函数 f (x) x2 cx的
最小值小于 1 .如果“ p或q ”为真，且“ p且q ”为假， 16
则实数 c 的取值范围为___0_,_1_2____. 1,
自学指导：
1、了解逻辑联结词“且”“或”“非”
的含义。 p q p q ┐p
高中选修《数学2-1》（新教材）
1.3 简单的逻辑联结词
逻辑联结词“且”“或”“非” 的含义
且：就是两者都有的意思。 或：就是两者至少有一个的意思（可兼容） 非：就是否定的意思。
注意:今后常用小写字母p,q,r,s,…表示命题。 我们把使用逻辑联结词联结而成的命题称为
复合命题。
(and)
观察下面的三个命题，它们之间有什么关系？
的(2)含.判义断; 复合命题的真假。
能力目标： (1).启发学生能够发现问题和提出问题，善于独立思考，
学会分析问题和创造地解决问题； (2).通过教师指导发现知识结论，培养学生抽象概括能 力和逻辑思维能力。
德育目标： 激发学生学习数学的兴趣和积极性，陶冶学生的情操，
培养学生坚忍不拔的意志，实事求是的科学学习态度 和勇于创新的精神。
课堂练习 3 答案:
1.若1≤
x
≤
2
,则
x2
1 3x
2
≤
0
或
x2 3x 2 0 .
2.若 x2 1 ,则 x 不一定等于 1.
课外练习:
1.设有两个命题，命题 p：关于 x 的不等式 (x2) x2 3x2≥0
的解集为{x | x ≥ 2} ，命题 q：若函数 y kx2 kx 1 的值恒
(4)“p∧q真”的充分不必要条件是
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
思考?
下列三个命题间有什么关系? (1)27是7的倍数； (2)27是9的倍数； (3)27是7的倍数或是9的倍数.
2、“或”（or）
一般地,用逻辑联结词“或”把命 题p和命题q联结起来.就得到一个新命
因为命题p是真命题，所以命题pVq是真命题.
(2)命题“集合A是A∩B的子集或是AUB的子集” 是由命题: p:集合A是A∩B的子集；q:集合A是 AUB的子集.用“或”联结后构成的新命题，即pVq.
因为命题q是真命题，所以命题pVq是真命题.
（3）命题“周长相等的两个三角形全等或面积 相等的两个三角形全等”是由命题：
命题的否定须注意的几个方面:
(1)“≥”的意义是“＞或＝”． (2)“非”命题对常见的几个正面词语的否定.
或 = > 是 都是 至多 至少 任 所 有一 有一 意 有 个 个 的的
且 ≠ ≤ 不 不都 至少 没有 某 某 是 是 有两 一个 个 些 个
我们先来看几个命题:
(1)10可以被2或5整除. (2)菱形的对角线互相垂直且平分. (3)0.5非整数.
p
q pVq p˄q
真真真 真
真假真 假 假真真 假
假假假 假
思考?
下列三个命题间有什么关系? (1)35能被5整除； (2)35不能被5整除.
3、“非”（not）
一般地,对一个命题p全盘否定,就 得到一个新命题,记作
p
读作“非p”或“p的否定”
p p
若p是真命题,则¬p必是假命题;若p 是假命题,则¬p必是真命题.
由于p是真命题,q是假命题,所以p˄q是假命题. (2)p˄q:菱形的对角线互相垂直且平分. 由于p是真命题,q是真命题,所以p˄q是真命题. (3)p˄q:35是15的倍数且是7的倍数. 由于p是假命题,q是真命题,所以p˄q是假命题.
例2 用逻辑联结词“且改写下列命题，并判断它们 的真假：
（1）1既是奇数，又是素数； （2）2和3都是素数. 解：（1）命题“11既是奇数，又是素数”可以 改写为“1是奇数且1是素数”.因为“1是素数” 是假命题，所以这个命题是假命题.
p:周长相等的两个三角形全等； q:面积相等的两个三角形全等 用“或”联结后构成的新命题，即pVq. 因为命题p，q都是假命题，所以命题pVq是 假命题.
思考?
如果p˄q为真命题,那么pVq一定是真 命题吗?
反之,如果pVq为真命题,那么p˄q一 定是真命题吗?
含有逻辑联结词“或”、“且”的命题的真假判
1.3简单的逻辑联结词： 或且非
思考?
下列三个命题间有什么关系? (1)12能被3整除; (2)12能被4整除; (3)12能被3整除且能被4整除.
1、“且”（and）
一般地,用逻辑联结词“且”把命题p 和
p ∧ q 命题q联结起来,就得到一个新命题,记作
读作“p且q”.
规定:当p,q都是真命题时, p˄q 是真命题;当p,q两个命题中有一个 命题是假命题时, p˄q是假命题.
“或”,“且”, “非”称为逻辑联结词. 含有逻辑联结词的命题称为复合命题,不含逻 辑联结词的命题称为简单命题.
复合命题有以下三种形式: (1)p˄q. (2)pVq. (3)¬p.
逻辑联结词“或”“且”“非”的含义
或：就是两者至少有一个的意思（可兼容） 且：就是两者都有的意思 非：就是否定的意思
例4 写出下列命题的否定，并判断它们的真假： (1)p:y=sinx是周期函数; (2)p:3<2; (3)p:空集是集合A的子集. 解:(1)¬p:y=sinx不是周期函数. 命题p是真命题,¬p是假命题.
(2)¬p:3≥2. 命题p是假命题，¬p是真命题.
(3)¬p:空集不是集合A的子集. 命题p是真命题，¬p是假命题.
全真为真,有假即假.
p q p˄q
真 真真 真 假假 假 真假 假 假假
p
q
例1、将下列命题用“且”联结成新命题，并
判断它们的真假： （1）p:平行四边形的对角线互相平分，
q:平行四边形的对角ห้องสมุดไป่ตู้相等；
（2）p:菱形的对角线互相垂直，
q:菱形的对角线互相平分；
（3）p:35是15的倍数，q:35是7的倍数. 解:(1)p˄q:平行四边形的对角线互相平分且相等.
题,记作 p q
规定：当p,q两个命题中有一个是 真命题时,pVq是真命题;当p,q两个命 题都是假命题时,pVq是假命题.
有真即真，全假为假
p q pVq
真 真真 真 假真 假 真真 假 假假
p q
例3 判断下列命题的真假：
(1)2≤2; (2)集合A是A∩B的子集或是AUB的子集； (3)周长相等的两个三角形全等或面积相等的 两个三角形全等. 解：(1)命题“2≤2”是由命题： p:2=2；q:2<2 用“或”联结后构成的新命题，即pVq.