竖曲线内任一点高程计算程序
竖曲线高程计算及程序设计

竖曲线高程计算及程序设计高永刚(中港一航局四公司云南嵩待项目部 ,云南 昆明 651700)[ 摘 要 ] 本文对道路施工中竖曲线中几种构成方式进行讨论并给出其计算公式 ,并结合 PC - 进行了程序设计 。
[ 关键词 ] 竖曲线 ;高程E500S[ 文章编号 ] 1007 - 3000 (2002) 01 - 0029 - 03[ 中图分类号 ] P258[ 文献标识码 ] A概述随着高等级公 路 建 设 中 路 面 高 程 测 量 精 度 求越来越高 ,原有的设计高程己无法满足施工 量的需要 ,从而使测量人员必须对路面点高程 行加密计算 。
对于纵断面中 未 设 竖 曲 线 部 分 的 高 程 计 算 对简单 , 而对竖曲线部分则 计 算 量 大 , 并 且 往 由于考虑不周而算错 ,随着 E 500S 、微机等在测 中应用 , 通过程序设计可方 便 快 捷 、准 确 的 实 路面点高程计算 。
竖曲线1 高程改正值 y 及曲线要素如图 1 ,两相邻纵坡的坡度为 i 1 、i 2 ,竖曲线半 为 R 。
(1) 竖曲线转角 :α= i 1 - i 2 (2) 曲线长 : L = R α= R ( i 1 - i 2 ) (3) 切线长 : T = Rtan (α/ 2)(4) 由于α很小 ,故可以认为曲线上各点 y 坐标方向与半径方向一致 ,也可认为它是切线上与 曲线上高程差 ,故( R + y ) 2 = R 2 + x 2又 y 2 与 x 2 相比较 ,其值甚微 ,可略去不计 2y ≈X从而 2Rx —坚曲线上任一点 P 至竖曲线起点或终点的水平距离2 . 2 高程计算 坚曲线的形式 通 常 由 两 相 邻 纵坡 的 大 小 所决定 ,其可分凹形和凸形 。
( 通 常 设 计 中 变 坡 点 高程 H b 、ZH b ,半径 R 及 i 1 、i 2 为已知)2 . 2 . 1 凸形竖曲线 凸形竖曲线设 计 是 沿 路 线 前进 方 向 连 接 两纵坡中 i 1 > i 2 的情形而设计的 ,具体构成及曲线 上任意高程计算如下 :图 1图 2Ξ [ 收稿日期 ] 2001 - 10 - 18(1) i 1 > 0 ,i 2 < 0 ,如图 2a :当 ZHb - T Φ ZH i Φ ZH b 时 , P i1 相对变坡点为下坡点 :H i 1 = H b - y - i 1 ×( ZH b - Z H i )b :当 ZH b ΦZH i ΦZH b + T 时 , Pi2 相对变坡点为下坡点 :下 :(1) i 1 Φ0 ,i 2 > 0 ,如图 5H i 2 = H b - y - i 2 ×( ZH i - (2) i 2 < i 1 , Φ0 ,如图 3ZH b ) 图 5Pi1 、Pi2 在变坡点任一侧相对变坡点都是上 坡a :当 ZHb - T ΦZH i ΦZH b 时 ,H i 1 = H b + y + i 1 ×( ZH b - b :当 ZH b ΦZH i ΦZH b + T 时 ,H i 2 = H b + y + i 2 ×( ZH i - (2) i 1 < i 2 Φ0 ,如图 6Z H i ) ZH b )图 3a :当 ZHb - T ΦZH i ΦZH b 时 , Pi1 相对变坡点为上坡点 :H i 1 = H b - y + i 1 ×( ZH b - b :当 ZH b ΦZH i ΦZH b + T 时 , Pi2 相对变坡点为下坡点 :H i 2 = H b - y - i 2 ×( ZH i - (3) i 1 > i 2 Ε 0 ,如图 4Z H i ) 图 6a :当 ZHb - T ΦZH i ΦZH b 时 , Pi1 相对变坡点为上坡点 :H i 1 = H b + y + i 1 ×( ZH b - b :当 ZH b ΦZH i ΦZH b + T 时 , Pi2 相对变坡点为下坡点 :H i 2 = H b + y - i 2 ×( ZH i - (3) i 2 > i 1 Ε 0 ,如图 7ZH b ) Z H i ) ZH b ) 图 4a :当 ZHb - T ΦZH i ΦZH b 时 , Pi1 相对变坡点为下坡点 :H i 1 = H b - y - i 1 ×( ZH b - b :当 ZH b ΦZH i ΦZH b + T 时 , Pi2 相对变坡点为下坡点 :H i 2 = H b - y + i 2 ×( ZH i - 2 . 2 . 2 凹形竖曲线Z H i ) ZH b )a :当ZHb - T ΦZH i ΦZH b 时, Pi1 相对变坡点为下坡点:H i 1 = H b + y - i1 ×( ZH b -b :当ZH b ΦZH i ΦZH b + T 时, Pi2 相对变坡点为下坡点:H i 2 = H b + y + i2 ×( ZH i -源程序:1000 : RE M 竖园曲线标高计算程序1005 :C LS :WA IT : PRINT“竖园曲线标高计算程序!”:WAIT(0)1010 :C LS : I NPUT“请输入变坡点桩号及高Z H i )程!BPDZH = ”:BPDZH“, BPD G C = ”:BPD G C1015 :C LS : INPUT“请输入竖园曲线的半径! ZH b)S QXB J = ”: S QXB J1020 :C LS : INPUT“请按路线前进方向输入变程序设计在竖曲线程序编辑中,要对其构成方进行全考虑,通过各种判断确定其形式和计算公式。
竖曲线高程计算公式

竖曲线上点的高程计算公式1.字母所代表的意义:R:曲线半径i1:ZY~JD方向的坡度1.字母所代表的意义:i0:路拱坡度i b:超高坡度L s:缓和曲线长精心整理精心整理b 1:所求点~路中线距离x 0:从直缓开始,到路左右坡度一致的距离,即图中C---Cx :所求点~直缓或缓直的距离h b :超高值超高计算公式1相对于路中线超高值行车道外侧边缘行车道内侧边缘X0=2×i0/(i0+ib)×Ls X≤x0hb=b1×(i0+ib)×X/Ls-b1×i0hb=-(b1+bx)×i0X≥x0hb=-(b1+bx)×X/LS×ib 行车道外侧边缘行车道内侧边缘hb=(-i0+(i0+ib)×X/Ls)×bhb=(-i0-(ib-i0)×X/Ls)×bi0:路拱坡度ib:超高坡度L s :缓和曲线长b:到路中线距离X:所求点到ZH(HZ)距离超高计算公式2()b si i L i x +=0002 1)当x ≤x 0时行车道外侧边缘:()0101i b L xi i b h sb b -+=行车道内侧边缘:()01i b b h x b +-=2)当x≥x0时行车道外侧边缘:()11i bLxiibhsbb-+=行车道内侧边缘:()bsxbiLxbbh+-=13.计算公式(公式2):精心整理。
竖曲线标高的计算及其程序应用

竖曲线标高的计算及其程序应用摘要根据竖曲线的原理,用CASIO-4500P袖珍计算机编制计算竖曲线标高的程序,在日常的计算工作中,取得了较好的效果。
介绍了竖曲线的理论参数和E=T/2R (1-3)Q=D-T,Z=D+T (1-4)竖曲线上的任一点距切线的纵距(亦称高程改正值)y为:y=x2/(2R) (1-5)上式中x为竖曲线上任一点至竖曲线起点或终点的水平距离。
y值在凹形竖曲线中为正值,在凸形竖曲线中为负值。
第二节竖曲线的手控计算设竖曲线半径R=20606.061,相邻坡段的坡度i1=2.55%、i2=4.2%,变坡点的里程桩号D为:K89+700,其高程G为936.335m,试求竖曲线的其它要素和K89+650、K89+730点的标高。
—、计算竖曲线的元素按1-1式得:T=0.5(2.55%-4.2%)×20606.061按1-2式得:L=2×170=340170按1-3式得:E=T2/2R=1702/(2×20606.061):0.701按1-4式得:Q=89700—170=89530,E=89700+170=89870二、计算K89+650和K89+730点的标高由于两坡道的坡度均为正值,i1< i2,故此竖曲线为凹形竖曲线,y取正值。
两点标高计算经过分别为:1、K89+650的标高计算过程:(1)此点距起点K89+530的平距:X=89650-89530=120(2)此点在切线上的坡道高程为:G·(D-89650) ×i1=936.335-(89700-89650) ×2.55%=935.06(3)此点的高差改正值为:y=x2/2R=1202/(2×20606.06)=0.349(4)此点的标高为:935.06+0.349=935.4092、K89+730点的标高计算经过:(1)此点距终点K89+870的平距:X=89870-89730=140(2)此点在切线上的坡道高程为:G+(89730-D) ×i2=936.335+(89730-89700) ×4.2%三937.595(3)此点的高差改正值:y=x2/(2R)=1402/(2×20606.061):0.476(4)此点的标高为:937.595+0.476=938.071第三节竖曲标高的计算程序及其应用一、程序的编制:(CASIO-4500P袖珍计算机程序)F1 SQL1 “MNRGDEF”L2 1--AbS(M—N):T--0.51R▲L=2T▲L3 Q=D-T▲Z=D+T▲L4 Lbl 1:{k}:K≤D ProgQJ:K>D ProgQH △△H▲GOTO 1F2 QJL1 H=G+E(D-K)M+F(K-Q)2/(2R)▲F3 QHL1 H=G-E(K-D)×N+F(Z-K)2/(2R) ▲二、程序说明1、程序输入M,N———分别为相邻纵坡的坡度,上坡为正值,下坡为负值;R———竖曲线的半径;D——竖曲线变坡点的里程;K——要求标高的里程;G———变坡点的高程;E——竖曲线为上坡时E=-I,竖曲线为下坡时,E=+1,当竖曲线由上坡变下坡,或由下坡变上坡时,E值应按曲线前后半部分视具体情况决定正负号。
竖曲线运算步骤及公式讲解

竖曲线上高程计算
已知:①第一坡度:i 1(上坡为“+”,下坡为“-”)
②第二坡度:i 2(上坡为“+”,下坡为“-”)
③变坡点桩号:S Z
④变坡点高程:H Z
⑤竖曲线的切线长度:T
⑥待求点桩号:S
计算过程:
1、切线上任意点与竖曲线间的竖距h 通过推导可得:
==PQ h )()(2112li y l x R y y A A q p ---=-R
l 22= 2、竖曲线曲线长: L = R ω
3.竖曲线切线长: T= T A =T B ≈ L/2 =
2ωR
4、竖曲线的外距: E =R
T 22
5. 竖曲线上任意点至相应切线的距离:R
x y 22= 式中:x —为竖曲任意点至竖曲线起点(终点)的距离, m ;
R —为竖曲线的半径,m 。
竖曲线计算的目的是确定设计纵坡上指定桩号的路基设计标高,其计算步骤如下:
(1)计算竖曲线的基本要素:竖曲线长:L ;切线长:T ;外距:E 。
(2)计算竖曲线起终点的桩号: 竖曲线起点的桩号 = 变坡点的桩号-T
(3)计算竖曲线上任意点切线标高及改正值:
切线标高 = 变坡点的标高±(x T -)⨯i ;改正值:y=R
x 22 (4)计算竖曲线上任意点设计标高
某桩号在凹形竖曲线的设计标高 = 该桩号在切线上的设计标高 + y 某桩号在凸形竖曲线的设计标高 = 该桩号在切线上的设计标高- y。
竖曲线标高计算程序

竖曲线标高计算程序(加了数据库)主程序名:SQXBGLbi1:{H}:H:Prog"SJK":F=C-D:T=Abs(RF÷2:R=R AbsF÷FH≤B-T=>K=0:≠=>H≥B+T=>K=0:C=D:≠=>K=H-B+T⊿⊿G=A-(B-H)C-K2÷2R▲Goto1 ――――――――――――――――――――――――――――――――――子程序:SJK H≤第二竖曲线起点桩号(5569.108)=>A=第一竖曲线交点高程(820.968):B=第一竖曲线交点桩号(4980):C=第一竖曲线前坡度(.03):D=第一竖曲线后坡度(-.02902):R=第一竖曲线半径(13000)⊿H≤第三竖曲线起点桩号(7174.4)=>A=第二竖曲线交点高程(798.331):B=第二竖曲线交点桩号(5760):C=第二竖曲线前坡度(-.02902):D=第二竖曲线后坡度(.0187):R=第二竖曲线半径(8000)⊿H≤第四竖曲线起点桩号(7898.584)=>A=第三竖曲线交点高程(828.438):B=第三竖曲线交点桩号(7370):C=第三竖曲线前坡度(.0187):D=第三竖曲线后坡度(.035):R=第三竖曲线半径(24000)⊿………………………继续添加要素――――――――――――――――――――――――――――――――――说明:1、A:交点高程2、B:交点桩号3、C:前坡度(上坡为正,下坡为负)4、D:坡度(上坡为正,下坡为负)5、R:竖曲线半径6、H:待求点桩号7、数据库中()内的数字用于网友试算,现根据()内的数据提供几个设计高程:H=5400 G=808.7796H=5450 G=807.3286H=6000 G=802.819H=6112 G=804.9134H=6980 G=821.145今天终于讲到了Excel函数的最后一部分——文本和数据函数。
再往后我们会陆续给大家介绍一些函数应用实例,每一则都会有详细的分析与指导,让您把理论上升为实际,敬请关注。
竖曲线任意里程中桩高程计算程序
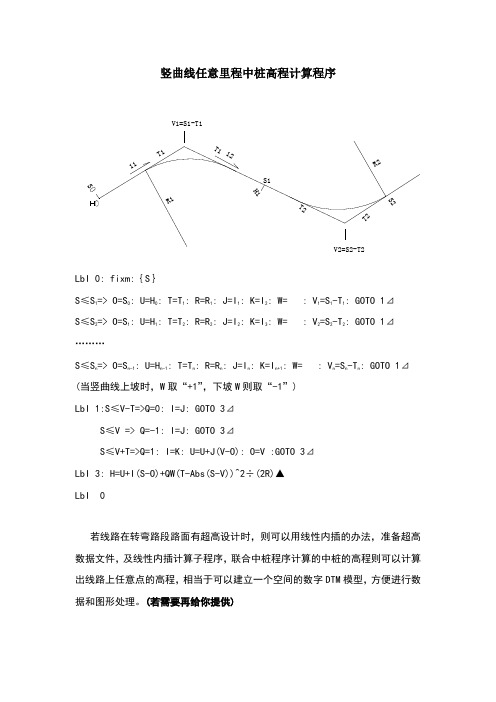
LbI 1:S≤V-T=>Q=0: I=J: GOTO 3⊿
S≤V => Q=-1: I=J: GOTO 3⊿
S≤V+T=>Q=1: I=K: U=U+J(V-O): O=V :GOTO 3⊿
LbI 3: H=U+I(S-O)+QW(T-Abs(S-V))^2÷(2R)▲
LbI0:fixm:{S}
S≤S1=> O=S0: U=H0: T=T1: R=R1: J=I1: K=I2: W= : V1=S1-T1: GOTO 1⊿
S≤S2=: J=I2: K=I3: W= : V2=S2-T2: GOTO 1⊿
………
S≤Sn=> O=Sn-1: U=Hn-1: T=Tn: R=Rn: J=In: K=In+1: W= : Vn=Sn-Tn: GOTO 1⊿
goto当竖曲线上坡时w取1下坡w则取1lbihuisoqwtabssv22rlbi若线路在转弯路段路面有超高设计时则可以用线性内插的办法准备超高数据文件及线性内插计算子程序联合中桩程序计算的中桩的高程则可以计算出线路上任意点的高程相当于可以建立一个空间的数字dtm模型方便进行数据和图形处理
竖曲线任意里程中桩高程计算程序
LbI 0
若线路在转弯路段路面有超高设计时,则可以用线性内插的办法,准备超高数据文件,及线性内插计算子程序,联合中桩程序计算的中桩的高程则可以计算出线路上任意点的高程,相当于可以建立一个空间的数字DTM模型,方便进行数据和图形处理。(若需要再给你提供)
竖曲线高程计算方法(一)
竖曲线高程计算方法(一)竖曲线高程计算在道路、桥梁、隧道等工程中,竖曲线是公路线形设计中的重要元素,而竖曲线高程计算则是道路设计过程中必不可少的一项工作。
本文将详细介绍竖曲线高程计算的各种方法。
直接法直接法是最简单的竖曲线高程计算方法,公式如下:H=R+L2 2R其中,H为竖曲线起点和终点高程差,R为竖曲线半径,L为竖曲线长度。
坡度法坡度法是一种常用的竖曲线高程计算方法,公式如下:H=∑(l i+l i+1)2d i24R ini=1其中,n为竖曲线段数,l i和l i+1分别为第i段和第i+1段的长度,d i为第i段的坡度,R i为第i段的半径。
求解法求解法是一种基于数值解的竖曲线高程计算方法,公式如下:H i=H i−1+l2(k i+k i−1)+l3240(k i−k i−1)2其中,H i为第i个点的高程,H i−1为第i−1个点的高程,l为第i个点和第i−1个点之间的水平距离,k i和k i−1分别为第i个点和第i−1个点的曲率。
分段求解法分段求解法是一种将竖曲线按照不同的半径等级分段求解的高程计算方法,公式如下:s iH i=H i−1+∫k(ρ(s))dss i−1其中,H i为第i个点的高程,H i−1为第i−1个点的高程,s i−1和s i分别为第i−1个点和第i个点之间的弧长,k(ρ(s))为曲率半径为ρ(s)时的曲率。
以上就是竖曲线高程计算的各种方法,根据不同的情况和要求,可以选择不同的方法进行计算。
混合法混合法是将直接法、坡度法、求解法和分段求解法结合起来的一种综合性高程计算方法,可以根据需要选择不同的计算方法进行竖曲线高程的计算。
混合法的具体过程如下:1.根据竖曲线长度和曲率要求选择直接法或坡度法计算竖曲线起点和终点的高程差。
2.确定分段长度和半径等级,使用分段求解法计算竖曲线半径变化较为平缓的区间的高程,并将计算结果与直接法或坡度法的计算结果进行校核。
3.使用求解法计算竖曲线半径变化较为显著的区间的高程,将计算结果与分段求解法和直接法或坡度法的计算结果进行校核。
竖曲线任意点高程计算例题
竖曲线任意点高程计算例题竖曲线是道路设计中常用的一种曲线形式,用于连接不同高程的道路段。
在竖曲线中,曲线是沿垂直方向变化的,通过控制曲率半径和高程变化率来实现。
在竖曲线设计中,一个重要的问题是如何计算曲线上各点的高程。
这需要根据设计要求和道路条件,使用相关的公式和计算方法进行求解。
首先,竖曲线设计中的一个重要参数是曲率半径。
曲率半径是曲线的弯曲程度的测量,在竖曲线中通常使用千分之一切割距(1/k)来表示。
常用的曲率半径有200、250、300等。
一般情况下,设计中需要根据道路的标准、设计速度等因素来确定曲率半径。
其次,竖曲线设计中需要考虑的另一个关键参数是纵坡。
纵坡是曲线的高程变化率,通常以百分比表示。
纵坡的选择需要考虑到各种因素,如舒适度、引导视线、排水等。
在设计中,一般规定了最大纵坡和最小纵坡范围,并根据道路的标准来选择合适的纵坡。
竖曲线设计中高程计算的基本方法是使用上拱曲线理论。
根据路线的设计要求和曲率半径,可以计算出曲线上各点的高程。
具体计算方法如下:1. 确定曲线起点和终点的高程,以及曲线起点的坡度。
在竖曲线设计中,通常规定曲线的起点和终点的高程,以及曲线起点的坡度。
这些信息是计算曲线高程的基础。
2. 将曲线分成若干段,并计算各段的水平长度和垂直位移。
根据曲线的设计要求和曲率半径,可以将曲线分成若干段,计算每段的水平长度和垂直位移。
3. 计算各点的高程。
根据曲线起点和终点的高程,以及曲线起点的坡度,可以计算出曲线上各点的高程。
4. 检查设计是否符合要求。
计算完成后,需要对设计进行检查,确保满足各种要求,如最大纵坡、最小纵坡、曲线长度等。
在竖曲线设计中,还可以使用各种软件进行高程计算。
常用的软件有AutoCAD、Civil 3D等,它们提供了方便快捷的计算功能,可以根据输入的参数自动生成曲线的高程。
总结起来,竖曲线任意点高程计算是道路设计中的重要一环。
通过确定曲率半径、计算水平长度和垂直位移,以及根据曲线起点高程和坡度计算各点高程,可以得到合理的竖曲线设计。
公路竖曲线高程计算程序
fx-4800P计算器公路竖曲线高程计算程序(程序名:GAO CHENG-HP)Lb1 0︰{CDAB}︰C“K1=”︰D“H1=”︰A“PV-K0=”︰B “PV-H0=”↙Lb1 1 ︰{REF }︰R“R=”︰E“K2=”︰F“H2=”↙Lb1 2︰U =(B-D)÷(A-C)︰V =(F-B)÷(E-A)︰U >V =>N = 0︰T = R ( U-V ) ÷2︰≠>N = 1︰T = R ( V-U ) ÷2 ︰⊿G = A -T ︰Q = A +T ︰W = T 2÷(2 R)↙Lb1 3︰{K}︰K “I.T.E.ZY-K.YZ-K=0,1”︰K =0 =>Goto 4 ︰⊿U “I 1”= U ▲V “I 2”= V ▲T = T ▲W “E”= W ▲G “ZY-K”= G ▲Q “YZ-K”= Q▲↙Lb1 4︰{M}︰M“PK=”︰M ≤A =>Goto 5︰⊿Goto 6 ↙Lb1 5︰M ≤G =>H = B-U ( A-M ) ︰Goto 7 ︰≠>Prog “H1 ”︰N = 1 =>H = B+X-Y ︰Goto 7︰≠>N = 0 =>H = B-X -Y ︰Goto 7↙Lb1 6︰M ≥Q =>H = B+V ( M-A ) ︰Goto 7 ︰≠>Prog “H2 ”︰N = 1 =>H = B+X+Y ︰Goto 7︰≠>N = 0 =>H = B-X +Y ↙Lb1 7︰H “HP”= H ▲{L}︰L“BZ-T=0,L”︰L = 0 =>Goto 8 ︰⊿{S}︰S “IL=”︰H “HL”= H +S L ▲↙Lb1 8︰{Z }︰Z “NEXT-PV=0,1”︰Z = 0 =>Goto 4 ︰⊿C= A ︰D= B ︰A =E ︰B= F ︰Goto 1↙子程序:H1:X = ( M-G ) 2÷( 2 R ) ︰Y = U ( A-M ) ↙H2:X = ( Q-M ) 2÷( 2 R ) ︰Y = V ( M-A ) ↙二00二年元月二十三日公路竖曲线高程计算程序(程序名:GAO CHENG-HP)使用说明1、按“ON”-“FILE”-“GAO CHEHG-HP”-“EXE”2、输入竖曲线后方直线段任一点桩号、高程(K1=?,H1=?),变坡点桩号、高程(PV-K0=?,PV-H0=?)-“EXE”3、输入竖曲线半径(R=?), 竖曲线前方直线段任一点桩号、高程(K2=?,H2=?) -“EXE”4、是否显示重要参数(后坡度%I1、前坡度%I2、以及竖曲线切线长T、外距E、曲线起点桩号ZY-K、曲线终点桩号YZ-K?,显示:输入1;不显示:输入0。
竖曲线高程计算公式
竖曲线上点的高程计算公式
1. 字母所代表的意义:
R:曲线半径
i1:ZY~JD方向的坡度
i2:JD~YZ方向的坡度
T:曲线的切线长
E:外失距
x:竖曲线上的点到直圆或圆直的距离
y:竖曲线上点的高程修正值
2. 计算公式:
超高计算公式
1. 字母所代表的意义:
i0:路拱坡度
i b:超高坡度
L s:缓和曲线长
b1:所求点~路中线距离
x0:从直缓开始,到路左右坡度一致的距离,即图中C---C
x:所求点~直缓或缓直的距离
h b:超高值
2. 计算公式公式1:绕中线旋转
1当x ≤x 0时
行车道外侧边缘:()0101i b L x
i i b h s
b b -+=
行车道内侧边缘:()01i b b h x b +-= 2当x ≥x0时
行车道外侧边缘:()0101i b L x
i i b h s b b -+= 行车道内侧边缘:()b s
x b i L x
b b h +-=
1 3. 计算公式公式2:
行车道外侧边缘:()100b L x i i i h s
b b ⎪⎪
⎭
⎫
⎝⎛
++
-= 行车道内侧边缘:()100b L x i i i h s
b b ⎪⎪
⎭
⎫
⎝⎛--
-=。
