matlab基础与应用教程答案
Matlab编程与应用习题和一些参考答案

Matlab编程与应用习题和一些参考答案Matlab 上机实验一、二3.求下列联立方程的解⎪⎪⎩⎪⎪⎨⎧=+-+-=-+=++-=--+41025695842475412743w z y x w z x w z y x w z y x >> a=[3 4 -7 -12;5 -7 4 2;1 0 8 -5;-6 5 -2 10];>> b=[4;4;9;4];>> c=a\b4.设⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡------=81272956313841A ,⎥⎥⎥⎦⎤⎢⎢⎢⎣⎡-----=793183262345B ,求C1=A*B’;C2=A’*B;C3=A.*B,并求上述所有方阵的逆阵。
>> A=[1 4 8 13;-3 6 -5 -9;2 -7 -12 -8];>> B=[5 4 3 -2;6 -2 3 -8;-1 3 -9 7];>> C1=A*B'>> C2=A'*B>> C3=A.*B>> inv(C1)>> inv(C2)>> inv(C3)5.设 ⎥⎦⎤⎢⎣⎡++=)1(sin 35.0cos 2x x x y ,把x=0~2π间分为101点,画出以x 为横坐标,y 为纵坐标的曲线。
>> x=linspace(0,2*pi,101);>> y=cos(x)*(0.5+(1+x.^2)\3*sin(x));>> plot(x,y,'r')6.产生8×6阶的正态分布随机数矩阵R1, 求其各列的平均值和均方差。
并求该矩阵全体数的平均值和均方差。
(mean var )a=randn(8,6)mean(a)var(a)k=mean(a)k1=mean(k)i=ones(8,6)i1=i*k1i2=a-i1i3=i2.*i2g=mean(i3)g2=mean(g)10.利用帮助查找limit 函数的用法,并自己编写,验证几个函数极限的例子。
MATLAB语言基础与应用(第二版)第5章 习题答案

第5章习题与答案5.1用矩阵三角分解方法解方程组123123123214453186920x x x x x x x x x +-=⎧⎪-+=⎨⎪+-=⎩ 解答:>>A=[2 1 -1;4 -1 3;6 9 -1] A =2 1 -1 4 -13 6 9 -1 >>b=[14 18 20]; b =14 18 20 >> [L, U, P]=lu(A) L =1.0000 0 0 0.6667 1.0000 0 0.3333 0.2857 1.0000 U =6.0000 9.0000 -1.0000 0 -7.0000 3.6667 0 0 -1.7143 P =0 0 1 0 1 0 1 0 0 >> y=backsub(L,P*b’) y =20.0000 4.6667 6.0000 >> x=backsub(U,y) x =6.5000 -2.5000 -3.5000 5.2 Cholesky 分解方法解方程组123121332352233127x x x x x x x ++=⎧⎪+=⎨⎪+=⎩ 解答:>> A=[3 2 3;2 2 0;3 0 12] A =3 2 32 2 03 0 12>> b=[5;3;7]b =537>> L=chol(A)L =1.7321 1.1547 1.73210 0.8165 -2.44950 0 1.7321>> y=backsub(L,b)y =-11.6871 15.7986 4.0415>> x=backsub(L',y)x =-6.7475 28.8917 49.93995.3解答:观察数据点图形>> x=0:0.5:2.5x =0 0.5000 1.0000 1.5000 2.0000 2.5000 >> y=[2.0 1.1 0.9 0.6 0.4 0.3]y =2.0000 1.1000 0.9000 0.6000 0.4000 0.3000 >> plot(x,y)图5.1 离散点分布示意图从图5.1观察数据点分布,用二次曲线拟合。
matlab基础教程课后答案

matlab基础教程课后答案【篇一:matlab基础练习题及答案】xt>1.4 matlab操作桌面有几个窗口?如何使某个窗口脱离桌面成为独立窗口?又如何将脱离出去的窗口重新放置到桌面上?答:在matlab操作桌面上有五个窗口。
在每个窗口的右上角有两个小按钮,一个是关闭窗口的close按钮,一个是可以使窗口成为独立窗口的undock按钮,点击undock按钮就可以使该窗口脱离桌面成为独立窗口。
在独立窗口的desktop菜单中选择dock...项就可以将独立的窗口重新放置到桌面上。
1.5 如何启动m文件编辑/调试器?答:在操作桌面上选择“建立新文件”或“打开文件”操作时,m文件编辑/调试器将被启动。
在命令窗口中键入edit命令时也可以启动m文件编辑/调试器。
1.6 存储在工作空间中的数组能编辑吗?如何操作?1.7 命令历史窗口除了可以观察前面键入的命令外,还有什么用途?答:命令历史窗口除了用于查询以前键入的命令外,还可以直接执行命令历史窗口中选定的内容、将选定的内容拷贝到剪贴板中、将选定内容直接拷贝到m文件中。
1.8 如何设置当前目录和搜索路径,在当前目录上的文件和在搜索路径上的文件有什么区别?答:当前目录可以在当前目录浏览器窗口左上方的输入栏中设置,搜索路径可以通过选择操作桌面的file菜单中的set path菜单项来完成。
在没有特别说明的情况下,只有当前目录和搜索路径上的函数和文件能够被matlab运行和调用,如果在当前目录上有与搜索路径上相同文件名的文件时则优先执行当前目录上的文件,如果没有特别说明,数据文件将存储在当前目录上。
1.9 在matlab中有几种获得帮助的途径?答:(1)帮助浏览器:选择view菜单中的help菜单项或选择help菜单中的matlab help菜单项可以打开帮助浏览器。
(2)help命令:在命令窗口键入“help” 命令可以列出帮助主题,键入“help 函数名”可以得到指定函数的在线帮助信息。
MATLAB基础及其应用教程-周开利-邓春晖课后答案,第三章
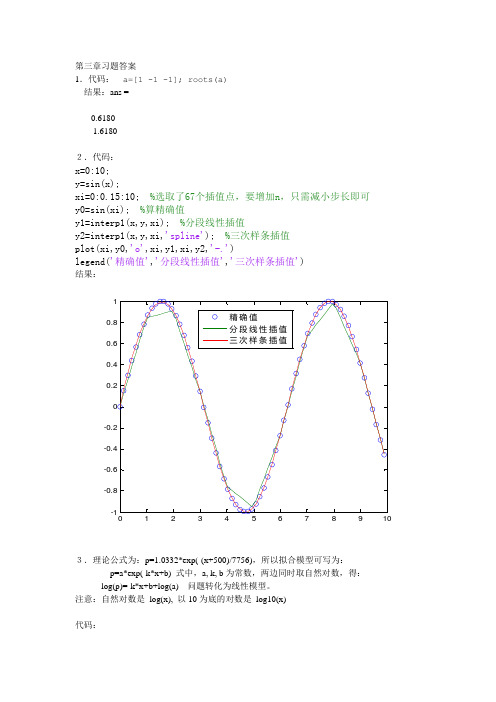
第三章习题答案1.代码:a=[1 -1 -1]; roots(a)结果:ans =-0.61801.61802.代码:x=0:10;y=sin(x);xi=0:0.15:10; %选取了67个插值点,要增加n,只需减小步长即可y0=sin(xi); %算精确值y1=interp1(x,y,xi); %分段线性插值y2=interp1(x,y,xi,'spline'); %三次样条插值plot(xi,y0,'o',xi,y1,xi,y2,'-.')legend('精确值','分段线性插值','三次样条插值')结果:3.理论公式为:p=1.0332*exp(-(x+500)/7756),所以拟合模型可写为:p=a*exp(-k*x+b) 式中,a, k, b为常数,两边同时取自然对数,得:log(p)=-k*x+b+log(a)问题转化为线性模型。
注意:自然对数是log(x), 以10为底的对数是log10(x)代码:clear;x=[0 300 600 1000 1500 2000];p=[0.9689 0.9322 0.8969 0.8519 0.7989 0.7491];lnp=log(p); %转化为 p 的自然对数值,模型转化为线性模型pk=polyfit(x,lnp,1); % 线性拟合,得到模型的斜率pk(1)和常数pk(2) 模型为: p=exp(pk(1)*x)*exp(pk(2))xi=0:50:2000;p0=1.0332*exp(-(xi+500)/7756); %理论值p1=exp(pk(1)*xi+pk(2)); %拟合模型值p2=interp1(x,p,xi,'spline'); %三次样条插值plot(x,p,'p',xi,p0,xi,p1,'--',xi,p2,'-.');legend('测量值','理论值','拟合值','三次样条值');format long % 数据显示格式为15位有效数字x2=0:200:2000 % 取10个点,比较差异pp1=1.0332*exp(-(x2+500)/7756) %理论值pp2=exp(pk(1)*x2+pk(2)) % 拟合值pp3=interp1(x,p,x2,'spline') % 样条插值err1=sum(abs(pp2-pp1).^2) % 拟合值的误差绝对值总和err2=sum(abs(pp3-pp1).^2) % 样条值的误差绝对值总和结果:0200400600800100012001400160018002000从图像上,都符合得很好,但很难看出差异。
matlab程序设计与应用第二版习题答案

matlab程序设计与应用第二版习题答案Matlab程序设计与应用第二版习题答案Matlab是一种强大的数学软件,广泛应用于科学计算、数据分析和工程设计等领域。
《Matlab程序设计与应用》是一本经典的教材,对于学习和掌握Matlab编程语言具有重要的意义。
本文将为大家提供《Matlab程序设计与应用第二版》中部分习题的答案,帮助读者更好地理解和应用Matlab。
第一章:Matlab基础1.1 基本操作1. a = 3; b = 4; c = sqrt(a^2 + b^2); disp(c);2. x = linspace(-pi, pi, 100); y = sin(x); plot(x, y);3. A = [1 2 3; 4 5 6; 7 8 9]; B = [9 8 7; 6 5 4; 3 2 1]; C = A + B; disp(C);1.2 控制结构1. for i = 1:10disp(i);end2. n = 0; sum = 0; while sum < 100n = n + 1;sum = sum + n;enddisp(n);3. x = 5; if x > 0disp('x is positive');elseif x < 0disp('x is negative');elsedisp('x is zero');end第二章:向量和矩阵运算2.1 向量运算1. A = [1 2 3]; B = [4 5 6]; C = A .* B; disp(C);2. A = [1 2 3]; B = [4 5 6]; C = A ./ B; disp(C);3. A = [1 2 3]; B = [4 5 6]; C = dot(A, B); disp(C);2.2 矩阵运算1. A = [1 2 3; 4 5 6]; B = [7 8; 9 10; 11 12]; C = A * B; disp(C);2. A = [1 2 3; 4 5 6]; B = [7 8; 9 10; 11 12]; C = B * A; disp(C);3. A = [1 2 3; 4 5 6]; B = [7 8; 9 10; 11 12]; C = A .* B; disp(C); 第三章:函数和脚本文件3.1 函数1. function y = myfunc(x)y = x^2 + 3*x + 2;end2. function [y1, y2] = myfunc(x1, x2)y1 = x1^2 + 3*x1 + 2;y2 = x2^2 + 3*x2 + 2;end3. function [y1, y2] = myfunc(x)y1 = x^2 + 3*x + 2;y2 = sin(x);end3.2 脚本文件1. x = linspace(0, 2*pi, 100); y = sin(x); plot(x, y);2. x = linspace(-10, 10, 100); y = x.^2 + 3*x + 2; plot(x, y);3. x = linspace(0, 2*pi, 100); y1 = sin(x); y2 = cos(x); plot(x, y1, x, y2);通过以上习题的答案,读者可以对Matlab程序设计的基本语法和常用函数有一个初步的了解。
MATLAB基础及其应用教程周开利邓春晖课后答案
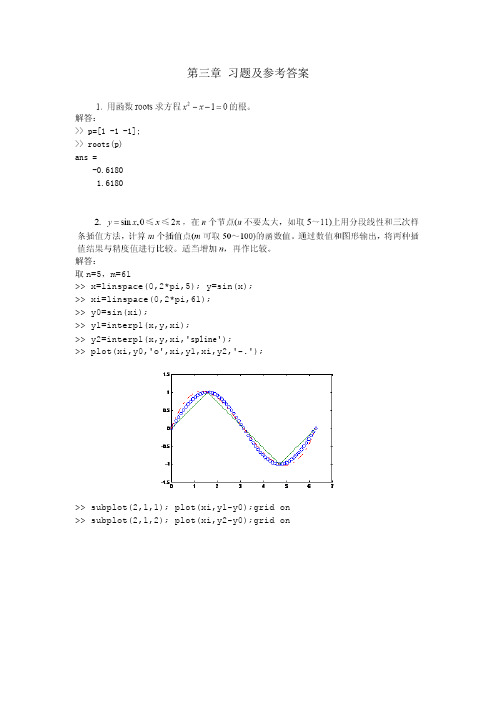
第三章习题及参考答案解答:>> p=[1 -1 -1];>> roots(p)ans =-0.61801.6180解答:取n=5,m=61>> x=linspace(0,2*pi,5); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on >> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差取n=11,m=61>> x=linspace(0,2*pi,11); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差解答:>> x=[0,300,600,1000,1500,2000];>> y=[0.9689,0.9322,0.8969,0.8519,0.7989,0.7491]; >> xi=0:100:2000;>> y0=1.0332*exp(-(xi+500)/7756);>> y1=interp1(x,y,xi,'spline');>> p3=polyfit(x,y,3);>> y3=polyval(p3,xi);>> subplot(2,1,1);plot(xi,y0,'o',xi,y1,xi,y3,'-.'); >> subplot(2,1,2);plot(xi,y1-y0,xi,y3-y0);grid on插值和拟合方法相比较,都合理,误差也相近。
MATLAB及其应用课后习题解答

5
“MATLAB 及其应用”课程作业
图 4- 2 画出函数图像
第5章
1. 已知椭圆的长、短轴 a 4, b 2 ,用“小红点线”画如下图所示的椭圆
x a cos t 。 y b sin t
(提示:参量 t ;点的大小;axis equal) 答 : 运 行 :clf; a=4;b=2;t=0:pi/80:2*pi;x=a*cos(t);y=b*sin(t);plot(x,y,’r’,’markersize’,15);axis equal;xlabel(‘x’);ylabel(‘y’);shg;结果如图 5-1 所示:
1
“MATLAB 及其应用”课程作业
a5=sin(sym(pi/4)+exp(sym(0.7+pi/3))); a6=sin(sym(pi/4)+sym(exp(0.7+pi/3))); a7=sin(sym(pi/4+exp(0.7+pi/3))); a8=sym(sin(pi/4+exp(0.7+pi/3))); da2 = vpa(a1-a2,30) da3 = vpa(a1-a3,30) da4 = vpa(a1-a4,30) da5 = vpa(a1-a5,30) da6 = vpa(a1-a6,30) da7 = vpa(a1-a7,30) da8 = vpa(a1-a8,30) 结果如图 2-2 所示: 只有 a2 是精准的,观察可知,这是由 于 sym('Num')和 sym(Num)的区别带来 图 2- 2 vpa 观察误差 的前者以字符串的形式传给符号运算内 核,可以保留完整的精度;而后者经过浮点数运算之后再转换为符号类型,存在精度损 失。 3.在不加专门指定的情况下,以下符号表达式中的哪一个变量被认为是独立自由变量。 sym('sin(w*t)') , sym('a*exp(-X)' ) , sym('z*exp(j*th)') 答:分别为 w,a,z,具体图 2-3 所示。
MATLAB基础及其应用教程周开利邓春晖课后答案

第三章习题及参考答案解答:>> p=[1 -1 -1];>> roots(p)ans =-0.61801.6180解答:取n=5,m=61>> x=linspace(0,2*pi,5); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差取n=11,m=61>> x=linspace(0,2*pi,11); y=sin(x);>> xi=linspace(0,2*pi,61);>> y0=sin(xi);>> y1=interp1(x,y,xi);>> y2=interp1(x,y,xi,'spline');>> plot(xi,y0,'o',xi,y1,xi,y2,'-.');>> subplot(2,1,1); plot(xi,y1-y0);grid on>> subplot(2,1,2); plot(xi,y2-y0);grid on分段线性和三次样条插值方法与精确值之差解答:>> x=[0,300,600,1000,1500,2000];>> y=[0.9689,0.9322,0.8969,0.8519,0.7989,0.7491]; >> xi=0:100:2000;>> y0=1.0332*exp(-(xi+500)/7756);>> y1=interp1(x,y,xi,'spline');>> p3=polyfit(x,y,3);>> y3=polyval(p3,xi);>> subplot(2,1,1);plot(xi,y0,'o',xi,y1,xi,y3,'-.');>> subplot(2,1,2);plot(xi,y1-y0,xi,y3-y0);grid on插值和拟合方法相比较,都合理,误差也相近。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8-1建立一个图形窗口,使之背景颜色为红色,并在窗口上保留原有的菜单项,而且在按下鼠标左键之后显示出Left Button Pressed 字样。
本体程序:
clc;
hf=figure('color','r','windowbuttondownfcn','axis off;text(0.1,0.5,''Left Button Pressed'',''fontsize'',30)')
运行结果:
hf =
1
8-3利用图形对象绘制下列曲线,要求先利用默认属性绘制曲线,然后通过图形句柄操作来改变曲线的颜色、线型和线宽,并利用文字对象给曲线添加文字标注。
(1)2)cos(2.0+=-x e y x
clc;
x=0:5*pi;
y=exp(-0.2*x).*cos(x)+2;
h=plot(x,y);
set(h,'Color',[1,0,0],'LineStyle',':','LineWidth',2);
(2)⎪⎩⎪⎨⎧==325t
y t x 程序:
t=0:2:100;
x=t.*t;
y=5*t.^3;
hf=plot(x,y);
set(hf,'color','b','linestyle',':','marker','p','linewidth',0.3);
8-4利用图形对象绘制下列三维图形,要求与上题相同。
(1)⎪⎩
⎪⎨⎧===t z t y t x sin cos
程序:
t=0:0.1:2*pi;
x=cos(t);
y=sin(t);
z=t;
hf=plot3(x,y,z);
运行结果:
8-5以任意位置子图形式绘制出正弦、余弦、正切和余切函数曲线。
clc;
x=-2*pi:0.01:2*pi;
y1=sin(x);
y2=cos(x);
axes('Position',[0.1,0.6,0.2,0.2])
plot(x,y1);
ht=get(gca,'Title');set(ht,'Color','r');title('y=sin(x)')
hc=get(gca,'Children'),set(hc,'Color','b','LineWidth',1.5)
axes('Position',[0.6,0.6,0.2,0.2])
plot(x,y2,'r');
ht=get(gca,'Title');set(ht,'Color','r');title('y=cos(x)')
axes('Position',[0.1,0.1,0.2,0.2])
fplot('tan(x)',[-1.5,1.5]);
ht=get(gca,'Title');set(ht,'Color','r');title('y=tan(x)')
axes('Position',[0.6,0.1,0.2,0.2])
fplot('cot(x)',[0,1,3]);
ht=get(gca,'Title');set(ht,'Color','r');title('y=cot(x)')。
