1描写刚体定轴转动的物理量(大学物理 - 刚体部分)
合集下载
大学物理第3章刚体的转动
T2
( 2 m1 m / 2 ) m 2 g m 2 M f / R m1 m 2 m / 2
例4.如图所示长度不等的A ,B两个匀质细棒(材料粗细均相 同), 从竖直位置由静止开始自由倒向地面,问:A B棒哪根先倒地?
M rF
M mg l 2 sin( )
三. 转动惯量
I
m
i 1
n
r i i
2
是刚体转动惯性大小的量度 (质量是物体惯性大小的量度) 1. 刚体的质量 由三个因素决定: 2. 质量的分布 3. 转轴的位置
物理意义:
M I
2 如果刚体是连续分布的质点系 I r d m 单位:kg m2
质量为体分布: d m d V 质量为面分布: d m d s
dm m l d x
1 2
1
l
I I
r
2
dm
O
dm
x
l
2
x dm
I
1 l
2
2 1 l 2
m l
l
m l
x dx
2
0
1 3
ml
2
x d x
l 2
2
z l
ml
2
3 mx l 3
l 2
1 12
o
dx
x
例2: 计算质量为m, 半径为R的均匀细圆环的转动惯量. 轴与圆环平面垂直并通过圆心。 解: 如图各质元到轴的垂直距离相等 m
质点角动量 L r p r m v
刚体的角动量(定轴转动)
L I
大学物理 刚体的定轴转动

⑶ t =6 ·0 s 时转过的角度为
6s
0
6s
d t 0
0(1et)dt
0 [te t]6 0 s 9 [6 ( 2 0 0) 5 (0 2 )]369rad
则 t =6 ·0 s
时电动机转过的圈数
N 587圈 2
5.2 5.4 刚体的转动定律及应用
5.2.1力对转轴的力矩
转轴
§5.1 刚体的运动的描述 §5.2 刚体定轴转动 §5.3 转动惯量的计算 §5.4 转动定律应用 §5.5 角动量守恒 §5.6 定轴转动中的功和能
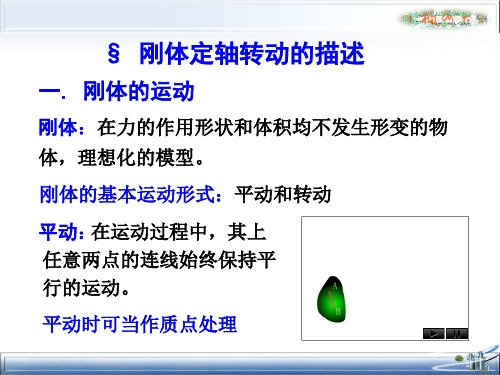
5.1 刚体的运动的描述
•刚体(rigid body)
任何情况下形状和体积都不改变的物体(理想化模型)。 刚体是特殊的质点系。 刚体可以看作是由许多质点组成,每一个质点叫做 刚体的一个质元,刚体这个质点系的特点是,在外 力作用下各质元之间的相对位置保持不变。
2、刚体定轴转动的转动定律
M d(J )dL J
dt dt
刚体绕定轴转动时,它的角加速度与作用于刚体上的 合外力矩成正比,与刚体对转轴的转动惯量成反比。
刚体定轴转动的转动定律
M=J 与 F ma地位相当 m反映质点的平动惯性,J 反映刚体的转动惯性
力矩是使刚体转动状态发生改变而产生角加速度的原因。力
ri
即 F itfitΔ m iri
则刚体转动定律为
变形有 F ir tifir tiΔm iri2
M J
对所有质元求和:
F ir ti fir ti (m ir i2 ) 上式表明:
这里 FitriM i M外
刚体绕定轴转动时,刚
fitri 0 定义 JΔmiri2 叫转动惯量
体的角加速度与它所 受的合外力矩成正比.
刚体的转动惯量(大学物理--刚体部分)解析ppt课件

第二节 转动惯量
1
一、转动惯量 刚体的动能等于各 质点动能之和。
2
刚体的动能 与平动动能比较
相当于描写转动惯性的物理量 转动惯量的定义: 单位: 千克 ·米2
3
§4.刚体的转动惯量/ 一、转动惯量
转动惯量
4
§4.刚体的转动惯量/ 二、转动惯量的计算
刚体的转动惯量与哪些物理量有关? ①.与刚体质量有关。 ②.与质量对轴的分布有关。 ③.与轴的位置有关。
细棒转轴通过中 心与棒垂直
l
细棒转轴通过端 点与棒垂直
14
§4.刚体的转动惯量\ 三、典型刚体的转动惯量
2r
2r
球体转轴沿直径
球壳转轴沿直径
15
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
四、平行轴定理 定理表述: 刚体绕平行于质心轴的转动惯 量 J,等于绕质心轴的转动惯量 JC 加上刚 体质量与两轴间的距离平方的乘积。
二.质量连续分布刚体的转动惯量计算
1.计算公式
5
§轻杆的 b 处 3b 处各系质量 为 2m和 m 的质点,可绕 o 轴转动,求: 质点系的转动惯量J。 解: 由转动惯量的定义
6
§4.刚体的转动惯量\ 二、转动惯量的计算
例2:长为 l、质量为 m 的匀质细杆,绕与 杆垂直的质心轴转动,求转动惯量 J。
建立坐标系,坐标原点选在边缘处。分 割质量元 dm ,长度为 dx ,
9
§4.刚体的转动惯量/ 二、转动惯量的计算
10
§4.刚体的转动惯量/ 二、转动惯量的计算
例4:半径为 R 质量为 M 的圆环,绕垂直 于圆环平面的质心轴转动,求转动惯量J。 解: 分割质量元 dm 圆环上各质量元到 轴的距离相等,
1
一、转动惯量 刚体的动能等于各 质点动能之和。
2
刚体的动能 与平动动能比较
相当于描写转动惯性的物理量 转动惯量的定义: 单位: 千克 ·米2
3
§4.刚体的转动惯量/ 一、转动惯量
转动惯量
4
§4.刚体的转动惯量/ 二、转动惯量的计算
刚体的转动惯量与哪些物理量有关? ①.与刚体质量有关。 ②.与质量对轴的分布有关。 ③.与轴的位置有关。
细棒转轴通过中 心与棒垂直
l
细棒转轴通过端 点与棒垂直
14
§4.刚体的转动惯量\ 三、典型刚体的转动惯量
2r
2r
球体转轴沿直径
球壳转轴沿直径
15
§4.刚体的转动惯量/ 三、典型刚体的转动惯量
四、平行轴定理 定理表述: 刚体绕平行于质心轴的转动惯 量 J,等于绕质心轴的转动惯量 JC 加上刚 体质量与两轴间的距离平方的乘积。
二.质量连续分布刚体的转动惯量计算
1.计算公式
5
§轻杆的 b 处 3b 处各系质量 为 2m和 m 的质点,可绕 o 轴转动,求: 质点系的转动惯量J。 解: 由转动惯量的定义
6
§4.刚体的转动惯量\ 二、转动惯量的计算
例2:长为 l、质量为 m 的匀质细杆,绕与 杆垂直的质心轴转动,求转动惯量 J。
建立坐标系,坐标原点选在边缘处。分 割质量元 dm ,长度为 dx ,
9
§4.刚体的转动惯量/ 二、转动惯量的计算
10
§4.刚体的转动惯量/ 二、转动惯量的计算
例4:半径为 R 质量为 M 的圆环,绕垂直 于圆环平面的质心轴转动,求转动惯量J。 解: 分割质量元 dm 圆环上各质量元到 轴的距离相等,
大学物理第3章刚体的定轴转动

13
【例5】长为 l、质量为 m 的匀质细杆,绕与杆垂直的 质心轴转动,求转动惯量 J。
【解】建立坐标系,分割质量元
J x2dm
l2 l 2
x2Байду номын сангаас
ml dx
1 ml 2 12
x o x dx
【例6】长为 l、质量为 m 的匀质细杆,绕细杆一端轴 转动,求转动惯量 J。
【解】J x2dm
L
L
11
【例2】半径为 R 质量为 M 的圆环,绕垂直于圆环平 面的质心轴转动,求转动惯量J。
【解】分割质量元,环上各质元到轴的距离相等。
M
J
R2dm R2
M
dm
MR2
0
0
【例3】在无质轻杆的 b 处 3b 处各系质量为 2m 和 m 的质点,可绕 O轴转动,求质点系的转动惯量J。
刚体作定轴转动时, 刚体上各质点都作圆周运动。 各质点运动的线量一般不同,但角量完全相同。
1.角坐标
OP与极轴之间的夹角称 为角坐标(或角位置)
角坐标为标量,但可有正负。
o
P
x
在定轴转动过程中,角坐标是时间的函数: =(t),称为转动方程。
3
2.角位移
角坐标的增量 称为刚体的角位移
i
i
i
得 LJ
v i m i ri
29
由刚体定轴转动定律
得到
MJ J
d dt
d( J ) dt
dL dt
M dL 定轴转动刚体角动量定理微分形式 dt
t
L
Mdt d
t0
L0
LLL0
1.3大学物理(上)刚体力学基础

dm ds dm dV
面密度和体密度。
线分布
面分布
体分布
注 意
只有对于几何形状规则、质量连续且均匀分布
的刚体,才能用积分计算出刚体的转动惯量。
[例3.1]: 求长为L、质量为m的均匀细棒对图中不同 轴的转动惯量。 [分析]:取如图坐标,dm=dx
A B
L
X
J A r dm
2
x dx mL / 3
T1 mg sin ma 1 2 T2 R T1 R J mR 2 mg T2 ma
a R
mg
[例3.4]: 转动着的飞轮的转动惯量为J,在t=0时角速度 为ω0。此后飞轮经历制动过程,阻力矩M的大小与角速度 ω的平方成正比,比例系数为k(k>0),当ω= ω0/3时,飞 轮的角速度及从开始制动到现在的时间分别是多少? [分析]: (1)已知 M k 2
练习:右图所示,刚体对经过
棒端且与棒垂直的轴的转动惯
mL
量如何计算?(棒长为L、球
半径为R)
mO
J L1
1 2 mL L 3
2 2 J o mo R 5
2 2
J L 2 J 0 m0 d J 0 m0 ( L R)
1 2 2 2 2 J mL L mo R mo ( L R) 3 5
dL d ( mv ) dr d (mv ) dr r mv F , v dt dt dt dt dt dL v mv 0, r F M r F v mv dt dL 角动量定理的微分形式 M dt
平均角速度
角速度
t
大学物理一复习第四章刚体的转动-文档资料

mg FT2 ma2
FT1 FT2
R
mg FT1 r
m
a1
J
a1 r
a2 R
FT1 r R
FT1'
A
mg
β
FT2
FT2'
B
mg
mg(R r)
J mR2 mr2
a1
r
J
mgr(R r) mR2 mr2
40 半径减小角速度增加。
(2)拉力作功。请考虑合外力矩为0, 为什么拉力还作功呢?
W
0
Md
在定义力矩作功 时,我们认为只 有切向力作功, 而法向力与位移 垂直不作功。
但在例题中,小 球受的拉力与位 移并不垂直,小 球的运动轨迹为 螺旋线,法向力 要作功。
o
F
r d Fn F
解得
a2
R
mgR(R r) J mR2 mr2
FT1 mg ma1
FT2 mg ma2
例2:光滑斜面倾角为 ,顶端固定一半 径为 R ,质量为 M 的定滑轮,质量为 m 的物体用一轻绳缠在定滑轮上沿斜面 下滑,求:下滑的加速度 a 。
解:物体系中先以
物体 m 研究对象,
A
分别根据牛二定律和转动定律列方程:
角量、线量关系式
解得:
a
mB g
mA mB mC 2
T1
mAmB g
mA mB mC
2
T2
(mA mC 2)mBg mA mB mC 2
如令 mC 0,可得:
大学物理Ⅰ刚体定轴转动的转动定律

第五章 刚体的定轴转动
5.1刚体运动的描述
一.刚体
刚体:在外力作用下,形状和大小都不发生变 化的物体 . (任意两质点间距离保持不变的特殊质点 组)
(1)刚体的运动
刚体的运动形式:平动、转动 .
平动:若刚体中所有点 的运动轨迹都保持完全相同, 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线 .
F F11 F
其中F11对转轴的力 矩为零,故 F 对转轴的力矩
M zk r F
z
k F11
F
O r
F
M z rF sin
2)合力矩等于各分 力矩的 矢量和 M M1 M2 M3
第五章 刚体的定轴转动
3) 刚体内作用力和反作用力的力矩互相抵消
M ij
O
rj
d ri
i
j
Fji Fij
M
rdf
l
grdr
0
1 gl 2
2
1 mgl
2
dm dl
dm ds
dm dV
其中、、分别
为质量的线密度、 面密度和体密度。
线分布
面分布
体分布
第五章 刚体的定轴转动
m 例1 一质量为 、长为 l 的均匀细长棒,求通过棒中
心并与棒垂直的轴的转动惯量 .
O
Or
l 2 O´ dr l 2
O´ dr l
r 解 设棒的线密度为 ,取一距离转轴 OO´ 为 处的质
fi
第五章 刚体的定轴转动
M i外 M i内 miri2
i
i
i
Mi内 0
i
M i外 ( miri2 )
i
i
z
O rj
5.1刚体运动的描述
一.刚体
刚体:在外力作用下,形状和大小都不发生变 化的物体 . (任意两质点间距离保持不变的特殊质点 组)
(1)刚体的运动
刚体的运动形式:平动、转动 .
平动:若刚体中所有点 的运动轨迹都保持完全相同, 或者说刚体内任意两点间的 连线总是平行于它们的初始 位置间的连线 .
F F11 F
其中F11对转轴的力 矩为零,故 F 对转轴的力矩
M zk r F
z
k F11
F
O r
F
M z rF sin
2)合力矩等于各分 力矩的 矢量和 M M1 M2 M3
第五章 刚体的定轴转动
3) 刚体内作用力和反作用力的力矩互相抵消
M ij
O
rj
d ri
i
j
Fji Fij
M
rdf
l
grdr
0
1 gl 2
2
1 mgl
2
dm dl
dm ds
dm dV
其中、、分别
为质量的线密度、 面密度和体密度。
线分布
面分布
体分布
第五章 刚体的定轴转动
m 例1 一质量为 、长为 l 的均匀细长棒,求通过棒中
心并与棒垂直的轴的转动惯量 .
O
Or
l 2 O´ dr l 2
O´ dr l
r 解 设棒的线密度为 ,取一距离转轴 OO´ 为 处的质
fi
第五章 刚体的定轴转动
M i外 M i内 miri2
i
i
i
Mi内 0
i
M i外 ( miri2 )
i
i
z
O rj
大学物理刚体的定轴转动
2l
l
17
例 一匀质细杆,长为 l 质量为 m ,在摩擦系数为
的水平桌面上转动,求摩擦力的力矩 M阻。 解: 建立如图坐标,取质元
dm dx
质元受阻力矩:
dM 阻 dmgx
o
xl dm m dx
x
细杆受的阻力矩
M阻
dM
阻
0l
gxdx
1 mgl
2
18
例 一半径为R,质量为m的均匀圆盘平放在粗糙的
令 J miri2
刚体绕Z轴转动的转动惯量
即
M z J ----刚体的定轴转动定律
说明
1. 上式是矢量式(力矩只有两个方向)。
2. M、J、是对同一轴而言的。
3. 具有瞬时性,是力矩的瞬时效应。
4. 转动惯量J是刚体转动惯性大小的量度。
8 8
3、转动惯量的计算
转动惯量: J miri2
l
r
dr
d
dm g
M
dM
l
0
mg l
r
cosdr
mg
l 2
cos
16
M J 1 ml2
3
3g cos
2l
(2) d d d d 3g cos dt d dt d 2l
分离变量积分 g cos d l d
02
03
(3g sin ) l
300 , 3g 900 , 3g
i
质量连续分布的刚体: J r2dm
质量为线分布: dm dl
面分布: dm ds
体分布: dm dV
1)总质量
转动惯量与下列因素有关: 2)质量分布 3)转轴位置
9
✓ J与质量分布有关:
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章刚体的转动
第一节 刚体定轴转动
一、什么是刚体?
物体的大小、形状和质量分布都不 随时间发生变化的物体。 二、刚体作定轴转动的特点 1.有一固定的轴。 2.刚体中各质点都作圆周运动。 3.各质点在相同的时间内转过的角度相同。
一.角坐标
描写刚体转动位置的物理量。
参考方向为ox,
刚体上某一点 P 到转轴 O 点 的连线与参考 方向ox的夹角。 单位:弧度,rad 角坐标为标量。
P
o
x
二、角位移 描写刚体位置变化的物理量。 刚体的角位移
P
x
0
单位:弧度,radFra biblioteko
0
三、角速度
θ dθ ω lim t 0 t dt
方向:满足右手定 则,沿刚体转动方 向右旋大拇指指向。
ω
四、角加速度 描写角速度变化快慢和方向的物理量。
v r
r
三、加速度与角加速度之间的关系 将质点的加 速度可分解为切 向加速度和法向 加速度,
dv d r a r dt dt 2 2 v (r ) 2 an r r r
o
a
r a n
a
a a a
2
2 n
2 ω dω dθ β lim 2 t 0 t dt dt
单位:弧度/秒2,rad/s2 方向: β
0
0
β
五、角量和线量的关系
一、位移与角位移之间的关系
r
s
s r
二、速度与角速度之间的关系
o
x
w v
s lim lim r t 0 t t 0 t
第一节 刚体定轴转动
一、什么是刚体?
物体的大小、形状和质量分布都不 随时间发生变化的物体。 二、刚体作定轴转动的特点 1.有一固定的轴。 2.刚体中各质点都作圆周运动。 3.各质点在相同的时间内转过的角度相同。
一.角坐标
描写刚体转动位置的物理量。
参考方向为ox,
刚体上某一点 P 到转轴 O 点 的连线与参考 方向ox的夹角。 单位:弧度,rad 角坐标为标量。
P
o
x
二、角位移 描写刚体位置变化的物理量。 刚体的角位移
P
x
0
单位:弧度,radFra biblioteko
0
三、角速度
θ dθ ω lim t 0 t dt
方向:满足右手定 则,沿刚体转动方 向右旋大拇指指向。
ω
四、角加速度 描写角速度变化快慢和方向的物理量。
v r
r
三、加速度与角加速度之间的关系 将质点的加 速度可分解为切 向加速度和法向 加速度,
dv d r a r dt dt 2 2 v (r ) 2 an r r r
o
a
r a n
a
a a a
2
2 n
2 ω dω dθ β lim 2 t 0 t dt dt
单位:弧度/秒2,rad/s2 方向: β
0
0
β
五、角量和线量的关系
一、位移与角位移之间的关系
r
s
s r
二、速度与角速度之间的关系
o
x
w v
s lim lim r t 0 t t 0 t
