大学物理第四章 刚体的转动(3课时)
合集下载
第4章刚体转动
16
长江大学物理教程
M1
外力在转动平面上对转
轴的力矩使刚体发生转动
F2
j2
F 2
F 1
r2 O r1
P2 d2 d1
P1
F1 力矩 M1 = r1 × F1 j1 大小 M1 = r1 F1 sin j1
= F1 d1 =F 1 r1
方向 MM2 = r2 × F2
M2
大小 M 2 = r2F2 sin j 2
定轴转动刚体在某时刻t 的瞬时角速度为 ，瞬
时角加速度 ， 刚体中一质点P至转轴的距离为r
瞬时线速度
质点P 瞬时切向加速度 瞬时法向加速度
的大小
2019/10/31
这是定轴转动中线量与角量的基本关系
11
长江大学物理教程
质点直线运动或刚体平动 位移 速度 加速度
匀速直线运动 匀变速直线运动
刚体的定轴转动 角位移 角速度 角加速度 匀角速定轴转动 匀变角速定轴转动
2019/10/31
12
长江大学物理教程
例1 在高速旋转的微型电动机里，有一 圆柱形转子可绕垂直其横截面并通过中心的 转轴旋转．开始起动时，角速度为零．起动
后式其中转m速随5时40间r变 s化1，关系为2.：0s ．求m (：1 et / )
(1)t=6 s时电动机的转速．(2)起动后，电动 机在 t=6 s时间内转过的圈数．(3)角加速度 随时间变化的规律．
优秀精品课件文档资料
长江大学物理教程
长江大学物理科学与技术学院
第四章 刚体的转动
主讲教师：喻秋山
2010～2011年第一学期
4-0 教学基本要求
一 理解描写刚体定轴转动角速度和 角加速度的物理意义，并掌握角量与线量 的关系．
大学物理。刚体转动课件
解：杆上各质元均 受摩擦力作用， 受摩擦力作用，但 各质元受的摩擦阻 力矩不同， 力矩不同，靠近轴 的质元受阻力矩小， 的质元受阻力矩小， 远离轴的质元受阻 力矩大， 力矩大，
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
细杆的质量密度 m λ= l 质元质量 dm = λdx 质元受阻力矩
O
−l 2
O
l 2
r
dr
dr O´
O´
l
解 设棒的线密度为 λ ，取一距离转轴 OO´ 为 处的质量元 dm = λdr dJ = r 2 dm = λr 2 dr
r
1 3 J = 2λ ∫ r dr = λl 0 12 1 = ml 2 12
l/2 2
如转轴过端点垂直于棒
1 2 J = λ ∫ r dr = ml 0 3
4 –三 力矩 转动定律 转动惯量 2 转动惯量
2 j j j
第四章 刚体的转动
2
J = ∑ ∆m r , J = ∫ r dm
物理意义： 物理意义：转动惯性的量度 . 意义 转动惯性的计算方法 质量离散分布刚体的转动惯量
J = ∑ ∆m r = m r + m r + L
2 j j 2 11 2 2 2 j
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
3） 刚体内作用力和反作用力的力矩互相抵消 ） 刚体内作用力和反作用力的力矩互相抵消
v Mij
O
v rj
v Mji
d
v iF ri ij
j v Fji v
v v M ij = −M ji
4 – 2 力矩 转动定律 转动惯量
第四章 刚体的转动
大学物理第四章 刚体的转动部分的习题及答案
第四章 刚体的转动一、简答题：1、简述刚体定轴转动的角动量守恒定律并给出其数学表达式?答案：刚体定轴转动时，若所受合外力矩为零或不受外力矩，则刚体的角动量保持不变。
2、写出刚体绕定轴转动的转动定律文字表达与数学表达式?答案：刚体绕定轴转动的转动定律：刚体绕定轴转动时，刚体的角加速度与它所受的合外力矩成正比，与刚体的转动惯量成反比。
表达式为：αJ M =。
3、写出刚体转动惯量的公式，并说明它由哪些因素确定?答案：dm r J V⎰=2①刚体的质量及其分布；②转轴的位置；③刚体的形状。
二、选择题1、在定轴转动中，如果合外力矩的方向与角速度的方向一致，则以下说法正确的是 ( A )A.合力矩增大时，物体角速度一定增大；B.合力矩减小时，物体角速度一定减小；C.合力矩减小时，物体角加速度不一定变小；D.合力矩增大时，物体角加速度不一定增大2、关于刚体对轴的转动惯量，下列说法中正确的是 ( C ) A.只取决于刚体的质量，与质量的空间分布和轴的位置无关； B.取决于刚体的质量和质量的空间分布，与轴的位置无关； C.取决于刚体的质量，质量的空间分布和轴的位置；D.只取决于转轴的位置，与刚体的质量和质量的空间分布无关；3、有一半径为R 的水平圆转台，可绕通过其中心的竖直固定光滑轴转动， 转动惯量为J ，开始时转台以匀角速度0ω转动，此时有一质量为m 的人站住转台中心，随后人沿半径向外跑去，当人到达转台边缘时，转台的角速度为 ( A ) A.()2mR J J +ω B.()2Rm J J +ω C.20mR J ω D.0ω4、均匀细棒OA 可绕通过其一端O 而与棒垂直的水平固定光滑轴转动，如图所示。
今使棒从水平位置由静止开始自由下落，在棒摆动到竖直位置的过程中，下述说法哪一种是正确的? ( A )A.角速度从小到大，角加速度从大到小．B.角速度从小到大，角加速度从小到大．C.角速度从大到小，角加速度从大到小．D.角速度从大到小，角加速度从小到大．5、一圆盘正绕垂直于盘面的水平光滑固定轴O 转动，如图射来两个质量相同，速度大小相同，方向相反并在一条直线上的子弹，子弹射入圆盘并且留在盘内，则子弹射入后的瞬间，圆盘的角速度( C )A.增大B.不变C.减小 (D) 、不能确定6、在地球绕太阳中心作椭圆运动时，则地球对太阳中心的 ( B ) A.角动量守恒，动能守恒 B.角动量守恒，机械能守恒 C.角动量不守恒，机械能守恒 D.角动量守恒，动量守恒7、有两个半径相同,质量相等的细圆环A 和B ，A 环的质量分布均匀，B 环的质量分布不均匀，它们对通过环心并与环面垂直的轴的转动惯量分别为A J 和B J ，则 ( C )A.B A J J >；B.B A J J <；C.B A J J =；D.不能确定A J 、B J 哪个大。
第四部分刚体的转动教学-
y
y
dA
x
dy
hy
x
O
Q
O
解 设水深h，坝长L，在坝面上取面积元 dA Ldy
作用在此面积元上的力
dFpdApLdy
h100m
L1000m
y
令大气压为 p 0 ，则
pp0g(hy) h y
d F [p 0 g (h y)]L d y O
dA dy
x
F 0 h [p 0g (h y )]L d yp 0 L h 1 2g L h 2
解 （1）0 5πrads1, t = 30 s 时， 0.
设 t = 0 s 时， 0 0 .飞轮做匀减速运动
0 0 5 π ra d s 1 π ra d s 2
t 3 0
6
飞轮 30 s 内转过的角度
22 0 22 ((5 π π)26)75πrad
mB B
FT1
FT2
mAmBg mA mB
（2） B由静止出发作匀加速直线运动，下落的速率
v 2ay
2mBgy
mAmBmC/2
（3） 考虑滑轮与轴承间的摩
擦力矩 M f ，转动定律
RF T2RF T1M f J
F T1
结合（1）中其它方程
Mf
F T2
FT 1mAa
m BgF T2 m Ba
NmR 784N
0
解：飞轮匀减速制动时有角加速度
0
t
01000r/m in2000/60104.7rad/s
0 t5s 0020.9rad/s2
t
fr
N
外力矩是摩擦阻力矩，
角加速度为负值。
第四章 刚体的转动
1 1 2 2 E k＝ E ki mi ri ＝ 2 2
m r
2 i i
2
用转动惯量表示
1 2 E k＝ J 2
四、刚体绕定轴转动的动能定理 设在合外力矩M的作用下，刚体绕定轴转过的角 位移为dθ，合外力矩对刚体所作的元功为 d dW =M dθ,由转动定律 M J J dt 得 d d
M＝r F r Fi r Fi M i
M F1 r1 sin 1 F2 r2 sin 2 F3 r3 sin 3
单位： N.m 注意：力矩的单位和功的单位不是一回事，力矩的 单位不能写成焦耳。 与转动垂直但通过转轴的力对转动不产生力矩； 与转轴平行的力对转轴不产生力矩； 刚体内各质点间内力对转轴不产生力矩。 对于刚体的定轴转动，不同的力作用于刚体上的 不同位置（或不同作用方向）可以产生相同的效 果。
§4－2 力矩
转动定律
转动惯量
一、力矩 从转轴与截面的交点到力的作用线的垂直距离叫做力对 转轴的力臂。力的大小和力臂的乘积，就叫做力对转 轴的力矩。用M表示。 用矢量表示 M rF 或：
M＝Fr sin
若力F不在垂直与转轴的平面内，则可把该力分解为两个 力，一个与转轴平行的分力，一个在垂直与转轴平面 内的分力，只有后者才对刚体的转动状态有影响。 合力矩对于每个分力的力矩之和。
第四章 刚体的转动
§4－1 刚体的定轴转动 一、刚体
定义:在外力作用下形状和大小保持不变的物体称为刚体。 说明: 刚体和质点一样是一个理想化的力学模型； 刚体内任何两点之间的距离在运动过程中保持不变； 刚体可以看成一个包含由大量质点、而各个质点间距 离保持不变的质点系。
m r
2 i i
2
用转动惯量表示
1 2 E k＝ J 2
四、刚体绕定轴转动的动能定理 设在合外力矩M的作用下，刚体绕定轴转过的角 位移为dθ，合外力矩对刚体所作的元功为 d dW =M dθ,由转动定律 M J J dt 得 d d
M＝r F r Fi r Fi M i
M F1 r1 sin 1 F2 r2 sin 2 F3 r3 sin 3
单位： N.m 注意：力矩的单位和功的单位不是一回事，力矩的 单位不能写成焦耳。 与转动垂直但通过转轴的力对转动不产生力矩； 与转轴平行的力对转轴不产生力矩； 刚体内各质点间内力对转轴不产生力矩。 对于刚体的定轴转动，不同的力作用于刚体上的 不同位置（或不同作用方向）可以产生相同的效 果。
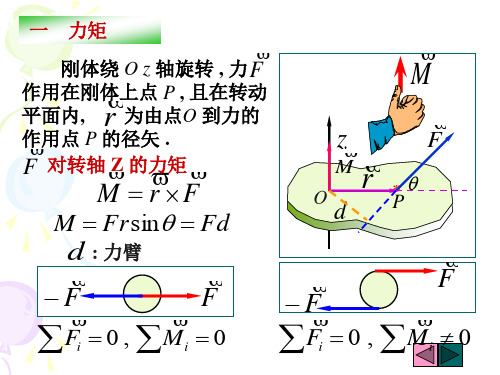
§4－2 力矩
转动定律
转动惯量
一、力矩 从转轴与截面的交点到力的作用线的垂直距离叫做力对 转轴的力臂。力的大小和力臂的乘积，就叫做力对转 轴的力矩。用M表示。 用矢量表示 M rF 或：
M＝Fr sin
若力F不在垂直与转轴的平面内，则可把该力分解为两个 力，一个与转轴平行的分力，一个在垂直与转轴平面 内的分力，只有后者才对刚体的转动状态有影响。 合力矩对于每个分力的力矩之和。
第四章 刚体的转动
§4－1 刚体的定轴转动 一、刚体
定义:在外力作用下形状和大小保持不变的物体称为刚体。 说明: 刚体和质点一样是一个理想化的力学模型； 刚体内任何两点之间的距离在运动过程中保持不变； 刚体可以看成一个包含由大量质点、而各个质点间距 离保持不变的质点系。
大学物理课件-刚体转动
d M K
dt I I
K dt d
I
tK
0 d
0
I
dt 2 0
t I ln 2 k
[例題]一繩跨過定滑輪，一端系品質為m的物體, 滑輪的
品質為m，半徑為R，轉動慣量為J＝mR2/2，可繞水準軸 自由轉動。繩與滑輪間無相對滑動. 求：物體的加速度和 繩的張力.
mg T ma TR J
O
任意質點i 的動能是
Eki
1 2
Dmii2
1 2
Dmi
ri2
2
剛體轉動動能是
Ek
i
Eki
1( 2
i
Dmi ri2 ) 2
Dmi
ri
i
Ek
1 2
I 2
m2>m1。滑輪可看作是品質均勻分佈的圓盤，品質為m，半徑為R， 轉動慣量為I＝mR2/2，可繞水準軸自由轉動。繩與滑輪間無相對滑 動。 求：物體的加速度和繩的張力。
解：
T1
(2m2
1 2
m1 m2
m )m1 g 1m
2
T2
(2m1
1 2
m1 m2
m )m2 g 1m
2
T a
2m1m2 m1 m2 m2 m1
解：根據牛頓定律、轉動定律
m2 g T2 m2a T1 m1 g m1a
T2 R T1R I
a R
a (m2 m1 )g
m1
m2
1 2
m
m1
m2
T1 T2
m1 g m2 g T1 T2
例3.5 一 繩 跨 過 定 滑 輪 ， 兩 端 分 別 系 品 質 為 m1 和 m2 的 物 體 ，
Lz ( Dmiri2) I
dt I I
K dt d
I
tK
0 d
0
I
dt 2 0
t I ln 2 k
[例題]一繩跨過定滑輪，一端系品質為m的物體, 滑輪的
品質為m，半徑為R，轉動慣量為J＝mR2/2，可繞水準軸 自由轉動。繩與滑輪間無相對滑動. 求：物體的加速度和 繩的張力.
mg T ma TR J
O
任意質點i 的動能是
Eki
1 2
Dmii2
1 2
Dmi
ri2
2
剛體轉動動能是
Ek
i
Eki
1( 2
i
Dmi ri2 ) 2
Dmi
ri
i
Ek
1 2
I 2
m2>m1。滑輪可看作是品質均勻分佈的圓盤，品質為m，半徑為R， 轉動慣量為I＝mR2/2，可繞水準軸自由轉動。繩與滑輪間無相對滑 動。 求：物體的加速度和繩的張力。
解：
T1
(2m2
1 2
m1 m2
m )m1 g 1m
2
T2
(2m1
1 2
m1 m2
m )m2 g 1m
2
T a
2m1m2 m1 m2 m2 m1
解：根據牛頓定律、轉動定律
m2 g T2 m2a T1 m1 g m1a
T2 R T1R I
a R
a (m2 m1 )g
m1
m2
1 2
m
m1
m2
T1 T2
m1 g m2 g T1 T2
例3.5 一 繩 跨 過 定 滑 輪 ， 兩 端 分 別 系 品 質 為 m1 和 m2 的 物 體 ，
Lz ( Dmiri2) I
大学物理学(上册)第4章 刚体的转动_OK
系统，其所受外力是两者的重力以及轴处轴对
l
杆的支持力，所有这些外力对轴的力矩为零，
因此系统对轴的角动量守恒.
m1
m10l
m11l
1 3
m2l 2
3m1(0 1) 25rad s-1
m2l
24
变为 ω2 ，积分可得：
t2 t1
Mdt
J2
J1
角动量定理积分形式
21
4.4.3 角动量守恒定律
定轴转动的角动量定理
M
dL dt
若 M 0 ， L 常矢量
对于某一固定轴，当刚体所受合外力矩为零时，其角动量 保持不变。(惯性系)-----角动量守恒定律
讨论
守恒条件 M 0
若 J不变， 不变；
若 J 变， 也变，但
L J 不变.
22
内力矩不改变系统的角动量.
在冲击等问题中 M内 M外 L 常量
角动量守恒定律是自然界的一个基本定律.
自然界中存在多种守恒定律
动量守恒定律 能量守恒定律 角动量守恒定律
电荷守恒定律 质量守恒定律 宇称守恒定律等
23
例1 如图所示，一竖直悬挂的木杆，可绕杆端O处的水平
动惯量为Jz，轴与平面的交点为O，物体绕平面内通过0点 相互垂直的两轴的转动惯量分别为Jx和Jy，则有：
Z
Jz Jx Jy
XO Y
o
o´
实心圆盘
16
例1. 求质量为m，长度为 L 的均质细棒的转动惯量。（转轴
oo´通过棒的一端并与棒垂直） 0
L
解：在距转轴x处，取质量元dm，
其长度为dx
0
x dx dm
J miri2 m1r12 m2r22 m3r32 i 1
大学物理B(上)第4章 刚体的转动
度 0 0，经300s 后，其转速达到 18000r·min-1 . 已知转
子的角加速度与时间成正比 . 问在这段时间内，转子转
过多少转？
（变角加速转动）
解:(1) 先求 ~ t 关系 由题意，令 ct，即 d ct，积分
dt
t
d c tdt
得 1 ct 2
z
r 刚体内任意一质元到转轴的垂直距离 i
v
转 ri P
动 平
θ
参
面
考
方
θ
向
线速度 i ri 切向加速度 ait ri
法向加速度 ain ri 2
ω
ω
定轴转动时，刚体上任意质元作圆周运动具有相同的，，
即定轴转动用角量描述最为方便。
4一– 1 刚刚体体的转定动轴的转角动速度和角加速度第四章 刚体的转动
4 – 1 刚体的定轴转动
第四章 刚体的转动
§4.1 刚体的基本运动(2)
4刚–体1 ：刚在体外的力定作轴用转下动，形状和大小都不第发四生章变刚化体的的物转体动 . （任意两质点间距离保持不变的特殊质点组） 刚体的运动形式：平动、转动 .
一. 平动
GTPD
刚体中所有点的运动轨迹都保持完全相同，或者说刚体内任 意两点间的连线总是平行于它们的初始位置间的连线 .
4例–11 刚一飞体轮的半定径轴为转动0.2m、 转速为150r第·m四in章-1，刚因体受的转制动 动而均匀减速，经 30 s 停止转动 . 试求：
(1)角加速度和在此时间内飞轮所转的圈数；
(2)制动开始后 t = 6 s 时飞轮的角速度；
(3)t = 6 s 时飞轮边缘上一点的线速度、切向加速度和法向加速度 .
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
r
Fz
q
F
4- 2
力矩 转动定律
转动惯量
（2） 外力矩与合外力矩 M1
外力在转动平面上对转 轴的力矩使刚体发生转动
F2
F 2
j2
r2
P2
O
r1
F 1
P1
F1
j1
d2 d1
力矩 M1 = r1 × F1 大小 M1 = r1 F1 sin j1
M2
合外力矩 大小
M = M1 + ቤተ መጻሕፍቲ ባይዱ 2
dy
y O Q
代入数据，得：
M 2.1410 N m
12
物理学
第五版
4-2
力矩
转动定律
转动惯量
二
转动定律
（1）单个质点 m 与转轴刚性连接
z
M
O
Ft
Ft mat mr
M rF sin θ
r
F
q m Fn
M rFt mr
2
M mr
2
4- 2
刚体的运动形式：平动、转动．
4-1 刚体的定轴转动
平 动
定轴转动
平面运动
定点运动 一般运动
刚体任意 刚体质心 刚体上 刚体每点 限制在一平 两点的连线 保持方向不 绕同一轴线 面内，转轴 各质点都 变。各点的 作圆周运动，可平动，但 以某一定 且转轴空间 始终垂直于 点为球心 位置及方向 该平面且通 的各个球 相同，可当 面上运动 不变。 过质心 作质点处理.
F Fi 0, M i 0 i i
F
4- 2
力矩 转动定律
转动惯量
讨论
（1）若力 F 不在转动平面内，把力分
解为平行和垂直于转轴方向的两个分量
力矩为零，故 F 对转 轴的力矩
其中 Fz 对转轴的
F Fz F
z
k
O
F
M z k r F M z rF sin q
4- 2
力矩 转动定律
转动惯量
例1 有一大型水坝高110 m、长1 000 m , 水深100m，水面与大坝表面垂直，如图所示. 求作用在大坝上的力，以及这个力对通过大坝 基点 Q 且与 x 轴平行的力矩 .
y
y
x
h
O Q O x
L
4- 2
力矩 转动定律
转动惯量
解 设水深h，坝长L，在坝面上取面积 元 dA Ldy ，作用在此面积元上的力
第五版
4-2
力矩
转动定律
转动惯量
例3 一质量为 m 、半径为 R 的均匀圆盘，求通 过盘中心 O 并与盘面垂直的轴的转动惯量.
解 设圆盘面密度为 ， 在盘上取半径为 ，宽为 dr 的圆环
r
圆环质量
dm 2 π r dr
dl
：质量线密度
对质量面分布的刚体： dm
：质量面密度
：质量体密度
dS
dV
对质量体分布的刚体：dm
物理学
第五版
4-2
力矩
转动定律
转动惯量
说明 刚体的转动惯量与以下三个因素有关： （1）与刚体的体密度 有关． （2）与刚体的几何形状及体密度 的分 布有关． （3）与转轴的位置有关．
O
ji
ri
Fi sin j i + f i cosq i
=
a i
=
ri
等式两边乘以 i 并对所有质元及其所受力矩求和
r
ri ri
得
M
=
∑
4- 2
力矩 转动定律
转动惯量
（2）刚体
瞬时 角加速度
瞬时 角速度
M
=
称为
∑
ri
Fi
qi
n
fi
即
刚体所获得的角加速度
合外力矩 的大小成正比， 与刚体的转动惯量 成反比。
d r O´
解 设棒的线密度为 ，取一距离转轴 OO´ 为 处的质量元 dm dr dJ r 2dm r 2dr
r
1 3 J 2 r dr l 0 12 1 ml 2 12
l/2 2
如转轴过端点垂直于棒
1 2 J r dr ml 0 3
l 2
物理学
1 2 2
1 2 2
v v0 at
0 t
4-1 刚体的定轴转动
三 角量与线量的关系 dq ω dt 2 dω d q 2 dt dt v rωet
an
a r P
et v a
t
at r an rω
2
2 a ret rω en
O
ji
ri
与刚体性质及质量分布有 关的物理量，用 J 表示
转动惯量
刚体的转动定律
的大小与刚体受到的
物理学
第五版
4-2
力矩
转动定律
转动惯量
三
转动惯量
J m j rj2 , J r 2dm
j
物理意义：转动惯性的量度.
转动惯性的计算方法
质量离散分布刚体的转动惯量
2 j j 2 11 j
(3) 电动机转动的角加速度为
d m t / t / 2 2 e 540 πe rad s dt
4-1 刚体的定轴转动
例2 在高速旋转圆柱形转子可绕垂直 其横截面通过中心的轴转动．开始时，它的 角速度 ω0 0 ，经300 s 后，其转速达到 18 000 r· min-1 ．转子的角加速度与时间成正 比．问在这段时间内，转子转过多少转？
dF pdA pLdy
y
y
x
h y O Q
dA
dy
O
x
L
4- 2
力矩 转动定律
转动惯量
令大气压为 p0 ，则 p p0 g (h y)
dF PdA [ p0 g (h y)]Ldy
F [ p0 g (h y)]Ldy 0 y 1 2 p0 Lh gLh 2
4- 2
力矩 转动定律
转动惯量
一
力矩
z
O
M
右手法则判断方向 用来描述力对刚体的转动作用．
F 对转轴 z 的力矩
d r sin q 为力臂
F
M Fr sin q Fd M r F
合力为零时, 其合力矩不一定为零
r
d
*
P
q
F F Fi 0, M i 0 i i
4-1 刚体的定轴转动
物理学
第五版
4- 0
教学基本要求
一 理解描写刚体定轴转动角速度和 角加速度的物理意义，并掌握角量与线量 的关系．
二 理解力矩和转动惯量概念，掌握 刚体绕定轴转动的转动定理．
三 理解角动量概念，掌握角动量定 律，并能处理一般质点在平面内运动以及 刚体绕定轴转动情况下的角动量守恒问题.
复杂 的运动 与平动 的混合。
一
4-1 刚体的定轴转动 刚体转动的角速度和角加速度
刚体定轴转动 的运动方程 沿逆时针方向转动 q > 0 沿顺时针方向转动 q < 0 刚体
刚体中任 一点 (t+△t) (t)
参考 方向
1. 角坐标
转动平面（包含p并与转轴垂直）
2. 角位移
转轴
q q (t t) q (t)
= F1 d 1 = F 1 r1 方向 M M 2 = r 2 × F2 大小 M 2 = r 2F 2 sin F j2 = F2 d 2 = F 2 r2
M = F1 d 1
F 2 r2 F2 d 2 = F 1 r1 叉乘右螺旋
r
4- 2
力矩 转动定律
转动惯量
合力矩等于各分力矩的矢量和
d 解 令 ct，即 ct ，积分 dt 1 2 t 得 ct d c t d t 0 0 2
4-1 刚体的定轴转动
1 2 ct 2
当 t =300 s 时
18 000 r min 600π rad s
1
1
2 2 600 π π 3 c 2 rad s 2 t 300 75 1 2 π 2 ct t 2 150
M M1 M 2 M 3
j
（3）刚体内作用力和反作用力的力矩互相抵消．
M ij
Fji iF
ij
rj
O
M ji
d
ri
M内 M ij 0
i, j
Mij M ji
z
F
O
M 0
(4) 当作用力通过转轴时, 其力矩 为零. 如右图.
第四章 刚体的转动
物理学
第五版
4- 0
教学基本要求
四 理解刚体定轴转动的转动动能概 念，能在有刚体绕定轴转动的问题中正确 地应用机械能守恒定律． 能运用以上规律分析和解决包括质点 和刚体的简单系统的力学问题．
第四章 刚体的转动
物理学
第五版
第一节
第四章 刚体的转动
4-1 刚体的定轴转动
刚体：在外力作用下，形状和大小都不 发生变化的物体．(任意两质点间距离保持 不变的特殊质点组．) ⑴ 刚体是理想模型 说明： ⑵ 刚体模型是为简化问题引进的．
代入数据，得
h y
10
h
dA
dy
F 5.9110 N