六年级奥数下册综合题型训练(二)
六年级奥数专题 数论综合二(学生版)

学科培优数学“数论综合二”学生姓名授课日期教师姓名授课时长知识定位在整个数学领域,数论被当之无愧的誉为“数学皇后”。
翻开任何一本数学辅导书,数论的题型都占据了显著的位置。
在小学各类数学竞赛和小升初考试中,我们系统研究发现,直接运用数论知识解题的题目分值大概占据整张试卷总分的30%左右,而在竞赛的决赛试题和小升初一类中学的分班测试题中,这一分值比例还将更高。
知识梳理涉及知识点多、解题过程比较复杂的整数综合题,以及基本依靠数论手段求解的其他类型问题.例题精讲【试题来源】【题目】一台计算器大部分按键失灵,只有数字“7”和“0”以及加法键“+”尚能使用,因此可以输入77,707这样只含数字7和0的数,并且进行加法运算.为了显示出222222,最少要按“7”键多少次?【试题来源】【题目】有一批图书总数在1000本以内,若按24本书包成一捆,则最后一捆差2本;若按28本书包成一捆,最后一捆还是差2本书;若按32本包一捆,则最后一捆是30本.那么这批图书共有本.【试题来源】【题目】一个五位数恰好等于它各位数字和的2007倍,则这个五位数是 .【试题来源】【题目】在纸上写着一列自然数1,2,…,98,99.一次操作是指将这列数中最前面的三个数划去,然后把这三个数的和写在数列的最后面.例如一次操作后得到4,5,…,98,99,6;而两次操作后得到7,8,…,98,99,6,15.这样不断进行下去,最后将只剩下一个数,则最后剩下的数是 .【试题来源】【题目】有两种规格的9箱钢珠,每箱300个,甲种钢珠每个10克,乙种钢珠每个11克,将这9箱钢珠编为1~9号,然后依次从1~9号箱中取出20,21,22,23,24,25,26,27,28,个钢珠,这些钢珠共重5555克。
问:哪几箱是甲种钢珠?【试题来源】【题目】把除1外的所有奇数依次按一项,二项,三项,四项循环的方式进行分组:(3),(5,7),(9,11,13),(15,17,19,21),(23),(25,27),(29,3l,33),(35,37,39,41),(43),…….那么,第1994个括号内的各数之和是多少?【试题来源】【题目】2001个球平均分给若干人,恰好分完。
六年级奥数专项复习训练二(行程问题)

六年级奥数专项复习训练(二)行程问题1、—辆客车和一辆货车同时从AB 两地相对开出,经过8小时,相遇后两车都以原速继续前进,又经过6小时,货车到达A 地,客车离B 地还有35千米,AB 两地相距多少千米?2、一辆汽车往返于AB 两地,去时每小时行45千米,要使来回的平均速度为54千米.回来的速度是多少千米?3、已知甲、乙两车的速度比是5:4,乙车出发,从B 站开往A 站,开到离B 站120千米的地方时,甲车从A 站发车开往B 站,两车相遇的地方离B 、A 两站的距离比是4:3,A 、B 两站相距多少千米?4、甲、乙两辆汽车分别从A 、B 两地同时相对而行,当乙车行了甲车所行路程的65%时,正好与甲车在汽车总站相遇,这时甲车在原地检修,而乙车又继续向前行驶了54千米,结果乙车行的总路程比甲车行的总路程多26千米,甲车所行的路程是多少千米?5、甲乙两车同时从A 地开往B 地,甲车到达B 地后立即返回,两车在离B 地56千米处相遇,这时甲车共行了14小时,已知甲车每小时速度比乙车快16%,乙车每小时行多少千米?6、甲乙两车同时从两地相向而行,相遇时,如果甲车再向前行驶自己已行路程的 ,就与乙车已行的路程一样多;如果甲车少行8千米,就是乙车已行路程的3/4,乙车行了多少千米?7、大货车和小轿车从同一地点出发沿同一公路行驶,大货车先走2小时,小轿车出发后4小时追上了大货车;如果小轿车每小时多走8千米,出发后3小时就可追上大货车,大货车每小时走多少千米?8、王华在一段路上练习长跑,如果每小时多跑51千米,时间就变为原来的54,原来的速度是每小时多少千米?行程问题练习1、在男子100米短跑比赛中,细心的裁判发现,当小小到达终点时,小叮距终点还有10米,小铛则才跑了81米。
如果照这样的速度跑下去,当小叮到达终点时,小铛距终点还有多少米?2、甲、乙两人的速度比是9:10,甲、乙两人同时从两地相向而行,相遇时离中点5千米,相遇后两人继续前进,当乙到达甲的出发地时,甲离乙的出发地多少千米?3、兔子和乌龟同时从甲地去乙地,兔子的速度是乌龟的8倍,途中兔子睡了一觉,耽误了一段时间,这样乌龟到达乙地时,免子离乙地还有640米,已知兔子睡觉的一段时间内乌龟跑了10580米,甲乙两地相距多少米?4、某人从A地到B地,如果用每分钟90米的速度走,那么要迟到5分钟;如果他用每分钟100米的速度走.那么要迟到3分钟,AB两地相距多少千米?5、一艘轮船所带的燃料最多可用14小时,轮船去时顺风.每小时航行120千米,返回时逆风,每小时航行90千米,这艘轮船最多航行多少千米就需返航?行程问题练习3、在男子100米短跑比赛中,细心的裁判发现,当小小到达终点时,小叮距终点还有10米,小铛则才跑了81米。
六年级奥数专题 行程综合二(学生版)

学科培优 数学 “行程综合二” 学生姓名授课日期 教师姓名授课时长 知识定位 通常我们所接触的行程问题可以称作为“参考系速度为0”的行程问题,例如当我们研究甲乙两人在一段公路上行走相遇时,这里的参考系便是公路,而公路本身是没有速度的,所以我们只需要考虑人本身的速度即可。
但是在流水行船问题中,我们的参考系将不再是速度为0的参考系,因为水本身也是在流动的,所以这里我们必须考虑水流速度对船只速度的影响.重难点在于1.流水行船中的相遇与追击2.火车问题知识梳理知识点:行程综合(二)流水问题:顺水速度=船速+水速, 逆水速度=船速-水速. ( 其中为船在静水中的速度,为水流的速度)由上可得:船速=(顺水速度+逆水速度)÷2;水速=(顺水速度-逆水速度)÷2.流水行船中的相遇与追击:水船顺V V V +=水船逆V V V -=船V 水V(1)两只船在河流中相遇问题.当甲、乙两船(甲在上游、乙在下游)在江河里相向开出,它们单位时间靠拢的路程等于甲、乙两船速度和.这是因为:甲船顺水速度+乙船逆水速度=(甲船速+水速)+(乙船速-水速)=甲船船速+乙船船速.这就是说,两船在水中的相遇问题与静水中的及两车在陆地上的相遇问题一样,与水速没有关系.(2)同样道理,如果两只船,同向运动,一只船追上另一只船所用的时间,也只与路程差和船速有关,与水速无关.这是因为:甲船顺水速度-乙船顺水速度=(甲船速+水速)-(乙船速+水速)=甲船速-乙船速.也有:甲船逆水速度-乙船逆水速度=(甲船速-水速)-(乙船速-水速)=甲船速-乙船速.这说明水中追及问题与在静水中追及问题一样.由上述讨论知,解流水行船问题,更多地是把它转化为已学过的相遇和追及问题来解答火车问题⑴火车过桥时间是指从车头上桥起到车尾离桥所用的时间,因此火车的路程是桥长与车身长度之和.⑵火车与人错身时,忽略人本身的长度,两者路程和为火车本身长度;火车与火车错身时,两者路程和则为两车身长度之和.⑶火车与火车上的人错身时,只要认为人具备所在火车的速度,而忽略本身的长度,那么他所看到的错车的相应路程仍只是对面火车的长度.对于火车过桥、火车和人相遇、火车追及人、以及火车和火车之间的相遇、追及等等这几种类型的题目,在分析题目的时候一定得结合着图来进行.例题精讲【试题来源】【题目】两港相距 120 千米,甲船往返两港需 60 小时,逆流航行比顺流航行多用了 20 小时.乙船的静水速度是甲船的静水速度的 3 倍,那么乙船往返两港需要多少小时?【试题来源】【题目】一艘轮船顺流航行 120 千米,逆流航行 80 千米共用 16 时;顺流航行 60 千米,逆流航行 120 千米也用 16 时。
六年级下册数学试题-奥数专题12:圆和组合图形(二)(含解析)全国通用
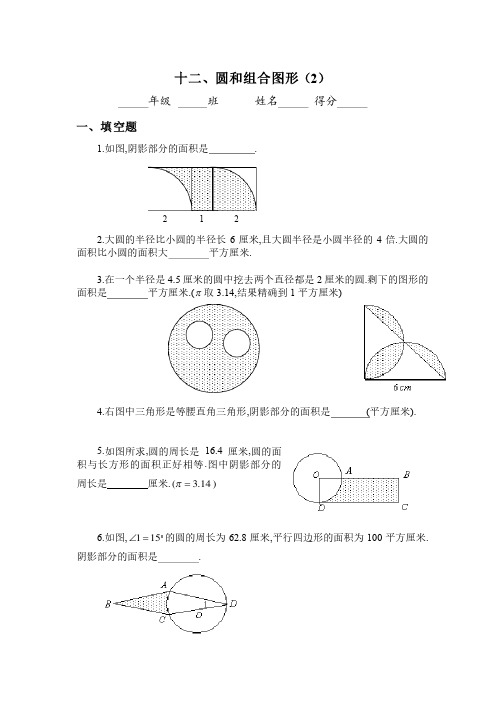
2 1 2 十二、圆和组合图形(2)年级 班 姓名 得分 一、填空题1.如图,阴影部分的面积是阴影部分的面积是 .2.大圆的半径比小圆的半径长6厘米,且大圆半径是小圆半径的4倍.大圆的面积比小圆的面积大面积比小圆的面积大 平方厘米.3.在一个半径是4.5厘米的圆中挖去两个直径都是2厘米的圆.剩下的图形的面积是面积是 平方厘米.(π取3.14,结果精确到1平方厘米)4.右图中三角形是等腰直角三角形,阴影部分的面积是阴影部分的面积是 (平方厘米).5.如图所求,圆的周长是16.4厘米,圆的面积与长方形的面积正好相等.图中阴影部分的周长是周长是 厘米.)14.3(=π6.如图,151=∠的圆的周长为62.8厘米,平行四边形的面积为100平方厘米.阴影部分的面积是阴影部分的面积是 .EDCB AG FO D CAB7.有八个半径为1厘米的小圆,用它们的圆周的一部分连成一个花瓣图形(如图).图中黑点是这些圆的圆心.如果圆周率1416.3=π,那么花瓣图形的面积是那么花瓣图形的面积是 平方厘米.8.已知:ABCD 是正方形, ED =DA =AF =2厘米,阴影部分的面积是阴影部分的面积是 .9.图中,扇形BAC 的面积是半圆ADB 的面积的311倍,那么,CAB ∠是 度.10.右图中的正方形的边长是2厘米,以圆弧为分界线的甲、乙两部分的面积差(大减小)是 平方厘米.(π取3.14)二、解答题11.如图:阴影部分的面积是多少?四分之一大圆的半径为r .(计算时圆周率取722)2甲乙12.已知右图中大正方形边长是6厘米,中间小正方形边长是4厘米求阴影部分的面积.13.有三个面积都是S 的圆放在桌上,桌面被圆覆盖的面积是2S +2,并且重合的两块是等面积的,直线a 过两个圆心A 、B , 如果直线a 下方被圆覆盖的面积是9,求圆面积S 的值.14.如图所示,一块半径为2厘米的圆板,从平面上1的位置沿线段AB 、BC 、CD 滚到2的位置,如果AB 、BC 、CD 的长都是20厘米,那么圆板的正面滚过的面积是多少平方厘米120ABCD12A B C a1OC B A E D———————————————答 案——————————————————————1. 6. 两个扇形面积相等,故阴影部分面积等于一个长为3,宽为2的长方形面积,为6个平方单位.2. 188.4.小圆的半径为2)14(6=-÷(厘米),大圆的半径为842=⨯(厘米).大圆的面积比小圆的面积大4.18814.3)28(22=⨯-(平方厘米). 3. 57.305.57214.3)22(14.35.422=⨯⨯÷-⨯(平方厘米)≈57(平方厘米). 4. 10.26.从圆中可以看出,阴影部分的面积是两个半圆的面积与三角形面积之差,即26.10621)26(14.322=⨯-÷⨯(平方厘米).5. 20.5.设圆的半径为r ,则圆面积即长方形面积为2r π,故长方形的长为r DC π=.阴影部分周长r r r r r r AD BA BC DC ππππ245241)(⨯=⨯+-++=+++= 5.204.1645=⨯=(厘米). 6. 6548(平方厘米).如图,连结OA 、AC ,过A 点作CD 的垂线交CD 于E .三角形ACD 的面积为502100=÷(平方厘米).又圆半径为10)214.3(28.6=⨯÷(厘米),因为151=∠, 又OA=OD ,故30215=⨯=∠AOC ,扇形AOC 的面积为的面积为61261014.3360302=⨯⨯(平方厘米).三角形AOC 的面积为25250=÷(平方厘米).方形面积为611256126=-(平方厘米),从而阴影部分的面积为654861150=-(平方厘米). 7. 19.1416.⌒E D C BAGF①②花瓣图形的结构是正方形的面积,加上四个43圆面积后,再割去四个半圆的面积.圆的半径为1厘米,正方形边长为4厘米.故花瓣图形的面积是故花瓣图形的面积是1416.1916421144314222=+=⨯⨯⨯-⨯⨯⨯+πππ(平方厘米).8. 2.43平方厘米. 如图,将①移到②得:阴影部分面积等于梯形CEFB 的 面积减去三角形CED 、三角形CDA 、扇形AFG 的面积,即 43.236045214.32122122212)322(22=⨯⨯-⨯-⨯⨯-⨯⨯⨯+(平方厘米).9. 60.设扇形ABC 圆心角的度数是x ,半圆的半径OA=r ,有2221311)2(360r r x⨯⨯⨯=⨯⨯ππ, 解得x=60. 10. 0.14.扇形面积为14.341214.32=⨯⨯(平方厘米),甲部分面积为43.0214.32122=÷-⨯(平方厘米),乙部分面积为57.04122214.3=⨯⨯-÷(平方厘米),甲乙两部分面积差为14.043.057.0=-(平方厘米).11. 如图,小正方形的边长为2r,则①的面积为: 72227224122r r r r =⨯-⎪⎭⎫⎝⎛⨯⨯, ②的面积为222417272221r r r =-⎪⎭⎫⎝⎛⨯⨯,①和②的面积和为2227224172241r r r =⨯⨯-⨯⨯.即阴影部分面积为272r . 12. 将阴影部分旋转后,可以看出所求阴影部分面积为大正方形面积的一半减去小正形的一半,即阴影部分面积等于10242622=÷-÷(平方厘米).13. 设一个阴影部分的面积为x ,则有:2223+=-S x S ,于是22+=x S(1) 又9232=-x S ,于是有23184+-=S x ,解得S=6.③①②14. 圆板的正面滚过的部分如右图阴影部分所求, 它的面积为:)420(4614)220(22122-+⨯⨯+⨯-+⨯⨯ππ 07.228323204221)24(414)220(4222≈+=⨯⨯+⨯-⨯-⨯-+⨯πππ(平方厘米).ABCD12。
小学六年级奥数专题之相遇问题

小学六年级奥数专题之相遇问题一、基本练习(1)甲、乙两列火车同时从相距700千米的两地相向而行,甲列车每小时行85千米,乙列车每小时行90千米,几小时两列火车相遇?(2)两列火车从两个车站同时相向出发,甲车每小时行48千米,乙车每小时行78千米,经过2.5小时两车相遇。
两个车站之间的铁路长多少千米?(3)甲、乙两列火车同时从相距988千米的两地相向而行,经过5.2小时两车相遇。
甲列车每小时行93千米,乙列车每小时行多少千米?二、综合练习(1)师徒两人合作加工520个零件,师傅每小时加工30个,徒弟每小时加工20个,几小时以后还有70个零件没有加工?(2)甲、乙两队合挖一条水渠,甲队从东往西挖,每天挖75米;乙队从西往东挖,每天比甲队少挖5米,两队合作8天挖好,这条水渠一共长多少米?(3)甲、乙两艘轮船从相距654千米的两地相对开出而行,8小时两船还相距22千米。
已知乙船每小时行42千米,甲船每小时行多少千米?(4)一辆汽车和一辆自行车从相距172.5千米的甲、乙两地同时出发,相向而行,3小时后两车相遇。
已知汽车每小时比自行车多行31.5千米,求汽车、自行车的速度各是多少?(5)两地相距270千米,甲、乙两列火车同时从两地相对开出,经过4小时相遇。
已知甲车的速度是乙车的1.5倍,求甲、乙两列火车每小时各行多少千米?(6)甲、乙两城相距680千米,从甲城开往乙城的普通客车每小时行驶60千米,2小时后,快车从乙城开往甲城,每小时行80千米,快车开出几小时后两车相遇?(7)甲、乙两车同时从相距480千米的两地相对而行,甲车每小时行45千米,途中因汽车故障甲车停了1小时,5小时后两车相遇。
乙车每小时行多少千米?(8)A、B两地相距3300米,甲、乙两人同时从两地相对而行,甲每分钟走82米,乙每分钟走83米,已经行了15分钟,还要行多少分钟才可以相遇?(9)甲、乙两列汽车同时从两地出发,相向而行。
已知甲车每小时行45千米,乙车每小时行32千米,相遇时甲车比乙车多行52千米。
六年级下册奥数试题-分数应用题(2) 通用版(无答案)

六年级奥数(分数应用题2)姓名1、(例)甲、乙、丙三人到银行存款,甲存入的款数比乙多51,乙存入的款数比丙多51,问甲存入的款数比丙多几分之几?2、甲、乙、丙三人合作生产一批机器零件,甲生产的零件数量的一半与乙生产零件数量的53相等,又等于丙生产的零件数量的43。
已知乙比丙多生产50个零件,问这批零件共有多少个?3、某学校四、五、六三个年级共有学生618人,其中五年级人数比四年级多101,六年级人数比五年级少101,求各年级学生人数。
4、甲、乙、丙、丁四人平均植树30多棵,甲植树棵数是乙的32,乙植树棵数是丙的411倍,丁比甲还多植树3棵,那么丙植树多少棵?5、(例) 甲、乙、丙、丁四人向希望工程捐款,甲的捐款数是另外三人捐款总数的31,乙的捐款数是另外三人总数的41,丙的捐款数是另外三人捐款总数的51,丁捐款460元。
求四人共捐款多少元?6、四个孩子合买一只60元的小船。
第一个孩子付的钱是其他孩子付的总钱数的一半。
第二个孩子付的钱是其他孩子付的总钱数的三分之一,第三个孩子付的钱是其他孩子付的总钱数的四分之一,第四个孩子付了多少钱?7、兄弟四人合作修一条路,结果老大修了另外三人总数的一半,老二修了另外三人总数的31,老三修了另外三人总数的41,老四修了91米,问这条路长多少米?8、育英小学四、五、六年级的学生栽树450棵。
已知四年级已经栽完了自己任务的65,五年级已经栽完了自己任务的32,六年级已经栽完了自己任务的95,并且他们已经栽完的棵数同样多。
问一共还剩下多少棵树没有栽?9、(例)3只猴子吃篮里的桃子,第一只猴子吃了31,第二只猴子吃了剩下的31,第三只猴子吃了第二只猴子吃过后剩下的41,最后篮子里还剩下6只桃子,问篮里原来有桃子多少只?10、修一条路,第一天修这条路的21还多2千米,第二天修余下的31少1千米,这样还剩下20千米没有修,求公路的长。
11、妈妈买了一些苹果。
小宇第一天吃去31又31个,第二天吃去剩下的41又41个,第三天吃去剩下的31又31个,这时还剩下3个苹果,问妈妈买了多少个苹果?12、某人拿了一筐桔子到集市上出售。
六年级下册奥数试题数的整除特征(二)全国通用(含答案)

第2讲数的整除特征(二)知识网络上一章我们已经学习了被2、3、5、8、9、25、125等整除的数的特征和一些整除的基本性质,但作为奥林匹克竞赛仅仅掌握以上知识还不够,这一讲继续学习有关数的整除知识。
(1)能被7、11和13整除的数的特征:如果一个数的末三位数字所表示的数与末三以前的数字所表示的差(一定要大数减小数)能被7、11或13整除,那么这个数就能被7、11或13整除。
(2)能被11整除的数的特征还有:一个数的奇数位上的数字之和与偶数位上的数字之和的差(大减小)是11的倍数。
重点·难点同学们在牢记上面整除的数的特征的同时,重点应弄清楚能被7、11、13整除的数为什么有上面的特征。
学法指导上面数的整除特征可以结合例子来理解。
例如:443716,判断它能否被7、11、13整除的方法是:716-443=273。
因为273能被7整除,所以443716能被7整除;因为273不能被11整除,所以443716不能被11整除;因为273能被13整除,所以443716能被13整除。
记忆要理论联系实际。
经典例题[例1]用1、9、8、8这四个数字能排成几个被11除余8的四位数?思路剖析能被11整除的数的特征是这个数的奇位数字之和与偶位数字之和的差能被11整除。
一个数要能被11除余8,那么这样的数加上3后,就能被11整除了,于是得到被11除余8的数的特征是:将偶位数字相加得到一个和数,再将奇位数字相加再加上3,得到另一个和数,如果这两个和数之差能被11整除,那么这个数就是被11除余8的数。
解答要把1、9、8、8排成被11除余8的四位数,可以把这四个数字分成两组,每组两个数字,其中一组作为千位和十位数,它们的和记作p,另外一组作为百位和个位数,它们之和加上3记作q,且p 和q的差能被11整除,满足要求的分组只可能是p=1+8=9,q=(9+8)+3=20,q-p=20-9=11,所以1988是被11除余8的四位数。
小学六年级奥数工程问题及答案(2)

小学六年级奥数工程问题1.甲乙两个水管单独开,注满一池水,分别需要20小时,16小时.丙水管单独开,排一池水要10小时,若水池没水,同时打开甲乙两水管,5小时后,再打开排水管丙,问水池注满还是要多少小时?2.修一条水渠,单独修,甲队需要20天完成,乙队需要30天完成。
如果两队合作,由于彼此施工有影响,他们的工作效率就要降低,甲队的工作效率是原来的五分之四,乙队工作效率只有原来的十分之九。
现在计划16天修完这条水渠,且要求两队合作的天数尽可能少,那么两队要合作几天?3.一件工作,甲、乙合做需4小时完成,乙、丙合做需5小时完成。
现在先请甲、丙合做2小时后,余下的乙还需做6小时完成。
乙单独做完这件工作要多少小时?4.一项工程,第一天甲做,第二天乙做,第三天甲做,第四天乙做,这样交替轮流做,那么恰好用整数天完工;如果第一天乙做,第二天甲做,第三天乙做,第四天甲做,这样交替轮流做,那么完工时间要比前一种多半天。
已知乙单独做这项工程需17天完成,甲单独做这项工程要多少天完成?5.师徒俩人加工同样多的零件。
当师傅完成了1/2时,徒弟完成了120个。
当师傅完成了任务时,徒弟完成了4/5这批零件共有多少个?6.一批树苗,如果分给男女生栽,平均每人栽6棵;如果单份给女生栽,平均每人栽10棵。
单份给男生栽,平均每人栽几棵?7.一个池上装有3根水管。
甲管为进水管,乙管为出水管,20分钟可将满池水放完,丙管也是出水管,30分钟可将满池水放完。
现在先打开甲管,当水池水刚溢出时,打开乙,丙两管用了18分钟放完,当打开甲管注满水是,再打开乙管,而不开丙管,多少分钟将水放完?8.某工程队需要在规定日期内完成,若由甲队去做,恰好如期完成,若乙队去做,要超过规定日期三天完成,若先由甲乙合作二天,再由乙队单独做,恰好如期完成,问规定日期为几天?9.两根同样长的蜡烛,点完一根粗蜡烛要2小时,而点完一根细蜡烛要1小时,一天晚上停电,小芳同时点燃了这两根蜡烛看书,若干分钟后来点了,小芳将两支蜡烛同时熄灭,发现粗蜡烛的长是细蜡烛的2倍,问:停电多少分钟?10、一项工程,甲先做2天,乙在做3天,完成全工程的四分之一,甲再做3天完成余下的四分之一,最后再由乙做,完成这项工作还要多少天?小升初数学专题之解方程一.字母的运算 =+x x 2 =-x x 312 =-x x %3543=+x x 56=-x x 5.0%75 =+a a 5.23 =+x x %33%25 =-x x 533=++x t x 543 =-+t x t 243 =+--t x t x 27326 =-+x x 5367二.去括号(主要是运用乘法的分配律和加减法的运算性质) 1.=+)(c b a 2.=++)(c b a =-+)(c b a3.=+-)(c b a=--)(c b a应用上面的性质去掉下面各个式子的括号,能进行运算的药进行运算 =-)3(3x=-)326(21x =++)23(12x =-+)3261(65x =--)3(5x =+-)1(27x =++)123(4183x x =--)312(36x x x=+++)62(31)43(21x x =--+)212(21)58(41x x 三.等式的性质.1.等式的定义: ,叫做等式;2.等式的性质:(1).等号的两边同时加上或减去同一个数,等号的左右两边仍相等; 用字母表示为:若a=b ,c 为任意一个数,则有a+c=b+c(a-c=b-c); (2).等号的两边同时乘以同一个数,等号的左右两边仍相等; 用字母表示为: ; (3).等号的两边同时除以同一个不为零的数,等号的左右两边仍相等. 用字母表示为: ; 四.方程1.方程的定义:含有未知数的等式叫做方程;2.方程的解:满足方程的未知数的值,叫做方程的解;3.解方程:求方程的解的过程,叫做解方程. 五.解方程1.运用等式的性质解简单的方程,257575575=-=-=-+=+x x x x 解:3399345345443543=÷==+=+=+-=-x x x x x x 解:如果把画框的部分省略,我们把一个数从等号的左边移到右边的过程,叫做移项, 注意把一个数从方程的左边移到右边时,原来是加的变成减,原来是减的变成加号。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
【例4】两名运动员在长为50米的游泳池里来回游泳。
甲运动员的速度是1米/
秒,乙运动员的速度是0.5米/秒,他们同时分别在游泳池的两端出发,来回共游了5
分钟,如果不计转向时间,那么这段时间里共相遇了几次?
一、画图解应用题技巧
【例1】甲、乙、丙、丁与小强五位同学一起比赛象棋,每两人都要比赛一盘。
到现在为止,甲已经赛了4盘,乙赛了3盘,丙赛了2盘,丁赛了1盘。
问:小强已
经赛了几盘?分别与谁赛过?
练习
1.三年级一班有
42人,全班都订了杂志。
订“少年文艺”的有38人,订“少
年科学画报”的有24人。
两种杂志都订的有多少人?
【例2】一群人在两片草地上割草,大的一片草地比小的正好大
体在大的一片草地干了半天,下午留下一半人在大草地上继续干,收工时正好把草割完;另一半人到小草地上干,收工时还余下一块地,这块地再用1人经1天
也可以割完。
问:这群干活的人共有多少位?
新-课-标-第-一-网w W w .X k b 1.c O m
2•有三堆围棋子,每堆棋子数相等。
第一堆中的黑子与第二堆中的白子一样多,
2
第三堆中的黑子占全部黑子的2,那么三堆棋子中,白子占全部棋子的几分之
5
几?
【例3】把一笔22500元的科研奖金发给一、二、三等奖获奖者,每个一等奖的奖金是每个二等奖奖金的2倍多500元,每个二等奖的奖金是每个三等奖的2倍, 一、二、三等奖的获奖者各是3人,那么每个一等奖的奖金是多少元呢?3•甲、乙两辆汽车同时从东、西两城相向而行,甲车每小时行42千米,乙车每小时行35千米,经过若干小时后,两车在离中点14千米处相遇。
两城之间的路程是多少千米?w W w .x K b 1.c o M
六年级奥数综合题型训练(二)
题型二解题技巧
1倍。
他们先全
4.甲、乙两车同时从A、B两地出发相向而行,两车在离B地64千米处第一次相遇。
相遇后两车仍以原速继续行驶,并且在到达对方出发点后,立即沿原路返回,途中两车在距A地48千米处第二次相遇,问两次相遇点相距多少千米?
二、用方程解应用题技巧
【例11某县农机厂加工车间有77个工人。
已知每个工人平均每天加工甲种零件5个或乙种零件4个或丙种零件3个。
但加工3个甲种零件、1个乙种零件和
9个丙种零件才恰好配成一套。
问:应安排生产甲、乙、丙种零件各多少人时, 才能使生产的三种零件恰好配套。
新课标第一网
【例2]某建筑公司有红、灰两种颜色的砖,红砖量是灰砖量的2倍,计划修建住宅若干座。
若每座住宅使用红砖80立方米,灰砖30立方米,那么,红砖缺
40立方米,灰砖剩40立方米。
问:计划修建住宅多少座?
【例3]两个数的和是100,差是8,求这两个数。
练习:
1.两个缸内共有48桶水,甲缸给乙缸加水一倍,然后乙缸又给甲缸加甲缸剩余水的一倍,则两缸的水量相等,求两个水缸原来各有多少桶水?
http://www.xkb 1 .com
2.早晨6点多钟有两辆汽车先后离开学校向同一目的地开去,6点32分时,第一辆汽车离开学校的距离是第二辆汽车的3倍。
到6点39分的时候,第一辆汽
车离开学校的距离是第二辆汽车的2倍,求第一辆汽车是6点几分离开学校的?
3.一人乘竹排沿江顺水漂流而下,迎面遇到一艘逆流而上的快艇,他问快艇驾驶员:“你后面有轮船开过来吗?” 快艇驾驶员回答:“半小时前我超过一艘轮船。
竹排继续顺水漂流了1小时遇到了迎面开来的这艘轮船。
那么快艇静水速度是轮
船静水速度的多少倍?
4•丢番图是古希腊著名的数学家,他的墓志铭与众不同,碑文是: “过路人!这
里埋葬着丢番图,他一生的六分之一是幸福的童年;又活了一生的十二分之一, 面部长起了胡须;随后是一生的七分之一的单身汉生活;婚后五年,他有了一个 儿子;可是,儿子活到丢番图一生年龄一半时,不幸夭折;儿子死后,父亲在深 深的悲哀中又过了 4年也与世长辞””你能计算出他一生中经历的主要年龄 吗?
【例4】计算:2 5 8 11 14
17 20
三、等差数列求和技巧
【例1】求1 2 3 •…+1998+1999的和。
都比前一天4页,最后一天读了 70页,刚好读完。
问:这本小说共多少页?
新-课-标-第-一-网
练习:
1.求 297 294 291 …9+6+3 的和。
【例3】求2 ~ A " 6 •…+196+198的
和。
【例5】小红读一本长编小说,第一天读了
30页,从第二天起,每天读的页数
【例2】求111
112 113 …+288+289的和。
2•求8000 -124 -128 -132 -…-272-276 的值。
【例3】若对所有a、b , b = a x , x是一个与b无关的常数;
頁 b = (a b)“2,且(1A3)^3=1A(3 ▽ 3)。
求(仏3)^ 2 的值。
三、解定义新运算的技巧
【例4】规定a:b = 4 a-3 b,已知8 _ (x: 1)=5,求x。
【例1】我们规定符号“O”表示选择两数中较大数的运算。
例如:30 2= 2O 3
=3。
符号“△”表示选择两数中较小数的运算,例如:3^ 2= 2^ 3= 2。
请计算:[(625 △ 630)] + (370O 375)] - (130 △ 125)
【例5】设玄※b表示a的3倍减去b的2倍,即玄※b=3a - 2b。
例如,当a = 6 ,
b = 5 时,6探5 = 3 6「2 5 = 8。
(1)计算:(1.6探0.8声 0.75 ;
(2)已知:乂※%※1) =7
a b 1
【例2】以玄※b表示,计算:(1992^996於(996探498)
b a 2
新课标第
网
练习:
1.如果:2T ( 3)表示 2 + 3+ 4=9 ;
(4)表示 5+ 6 + 7 + 8=26,那么 (100)
为( )。
A . 5000
B . 5550
C . 5500
D . 5555
2•如果“△◎口”表示△乘以△,再乘以□,那么下列数中,表示“
4© 3”所
得结果的数是(
)。
A . 12
B . 27
C . 36
D . 48
E . 64 X|k |B | 1 . c|0 |m
3. x 、y 表示两个数,规定两个新运算“※”及“△”: x 探y = mx • ny , x A y =
kxy ,
其中m 、n 、k 都是自然数。
已知 1探2= 5, (2探3)^ 4= 64,求(1 △ 2)探3的 值。
新课标第一网系列资料
4.对于两个数 a 、b , aA b=a + b — 1。
(1) 计算(1 △ 8)^ 6=?
(2) 已知(§△ x ) △ x = 84,求 x 。
5.对于两个数 x 、y , xO y 表示yX A — x X 2,并且已知 820 65=31,计算290 57的
值。
6.我们规定符号“二”表示选择两数中较大数的运算,符号“
:”表示选择
两数中较小数的运算,例如
5二3=3二5=5 , 5: 3=3: 5=3,试计算:
[(0.6 二 0.8) + (3: 3.1)] X [(2.1 : 2.11) — (0.21 二 2.10)]。
