机械控制工程之系统的数学模型
《机械控制工程基础》-2物理系统的数学模型及传递函数解析

称为叠加性或叠加原理。
控制工程基础
2.1.3 非线性系统的线性化
(2)非线性系统 如果系统的数学模型是非线性的,这种 系统称为非线性系统。 工程上常见的非线性特性如下: 饱和非线性 死区非线性 间隙非线性 摩擦非线性……
控制工程基础
2.1.3 非线性系统的线性化
(3)举例 下列微分方程描述的系统为线性系统:
零初始条件: 输入及其各阶导数在t =0-时刻均为0; 输出及其各阶导数在t =0-时刻均为0。 形式上记为:
Y (s) b0 s m b1s m1 bm1s bm G( s ) X (s) a0 s n a1s n1 an1s an
控制工程基础
2.2.2 传递函数的求法
(1)解析法(根据定义求取) 设线性定常系统输入为x(t) ,输出为y(t) ,描 述系统的微分方程的一般形式为 :
dny d n1 y d n2 y dy an n an1 n 1 an 2 n2 a1 a0 y dt dt dt dt
Xi ( s) Ts Xo ( s)
传递函数: G( s)
式中T为微分时间常数。
特点: (1)一般不能单独存在 (2)反映输入的变化趋势 (3)增强系统的阻尼 (4)强化噪声
4.积分环节
1 微分方程: xo (t ) T xi (t )dt
传递函数:
X ( s) 1 G( s) o X i (s) Ts
2 2
下列微分方程描述的系统为非线性系统:
控制工程基础
2.1.3 非线性系统的线性化
(4)系统运动微分方程的建立
电气系统
电阻、电感和电容器是电路中的三个基本元件。通常利用基尔霍夫 定律来建立电气系统的数学模型。 基尔霍夫电流定律:
机械控制工程基础习题集_234

13.不同属性的物理系统可以有形式相同的(A)
A.传递函数 B.反函数 C.正弦函数
D.余弦函数
14.比例环节能立即地响应(B)
A.输出量的变化 B.输入量的变化 C.误差量的变化 D.反馈量的变化
15.满足叠加原理的系统是(C)
1
A.定常系统 B.非定常系统 C.线性系统 D.非线性系统
16.弹簧-质量-阻尼系统的阻尼力与两相对运动构件的(B)
10.惯性环节:输出量 x0 和输入量 xi 的动力学关系为一阶微分方程Txo x0 Kxi 形式的
环节。
11.振动环节:输出量 x0 和输入量 xi 的动力学关系为二阶微分方程 T 2xo 2Txo x0 Kxi
形式的环节。 四、简答题 1 若力为输入、位移为输出时,写出如图所示机械系统的弹簧、粘性阻尼以及质量的传 递函数。
A.自身内部结构参数有关 B.输入信号有关 C.输出信号有关 D.干扰信号有关
23.闭环控制系统的开环传递函数是(C)
A.输出信号的拉氏变换与输入信号的拉氏变换之比
B.输入信号的拉氏变换与输出信号的拉氏变换之比
C.反馈信号的拉氏变换与误差信号的拉氏变换之比
D.误差信号的拉氏变换与反馈信号的拉氏变换之比
B G2 (s)
3.简述同一闭环控制系统的闭环传递函数与开环传递函数之间的特性关系。
答:1)闭环特征方程为开环传递函数有理分式的分母多项式与分子多项式之和; 2)闭环特征多项式和开环特征多项式具有相同的阶次;
3)闭环传递函数和开环传递函数具有相同的零点,但不存在公共极点。
4.说明同一闭环系统的闭环传递函数和开环传递函数具有相同的零点。
9.满足叠加原理的系统是(线性)系统。
2
机械工程控制基础系统的数学模型概述.pptx

微分方程一般形式:
anc(n)
a c(n1) n1
...
a1c
a0c
bm r (m)
b r (m1) m1
...
b1r
b0r(t )
拉氏变换: ansn an1sn1 .... a1s a0 C(s) bm sm bm1sm1 ... b1s b0 R(s)
§2.1 引言
•数学模型
描述系统输入、输出变量以及内部各变量之间关系 的数 学表达式
•建模方法
解析法(机理分析法)
根据系统工作所依据的物理定律列写运动方程
实验法(系统辨识法)
给系统施加某种测试信号,记录输出响应,并用 适当的数学模型去逼近系统的输入输出特性
§2.2 控制系统的数学模型—微分方程 线性定常系统微分方程的一般形式
di (t ) ur (t ) L dt Ri(t ) uc (t )
i(t ) C duc (t ) dt
LC
d
2uc (t ) dt 2
RC
duc (t ) dt
uc (t )
d 2uc (t ) dt 2
R L
duc (t ) dt
1 LC
uc (t )
1 LC
ur (t )
§2. 2. 1 线性元部件及系统的微分方程
k 1 v n1
s
l 1 n2
(Ti s 1)
(T
2 j
s
2
2Tj
s
1)
i 1
j1
§2.3 系统的复域模型—传递函数
例7 已知
G( s )
s3
4s 4 3s2
2s
将其化为首1、尾1标准型,并确定其增益。
机械控制工程基础第二章 控制系统的数学基础和数学模型

动态模型反映系统在迅变载荷或在系统不平衡状态下的特性,现时输出还
由受其以前输入的历史的影响,一般以微分方程或差分方程描述。在控制
理论或控制工程中,一般关心的是系统的动态特性,因此,往往需要采用
动态数学模型。
例:
••
•
系统动态模型:m x(t) c x(t) kx(t) F (t)
•
••
当系统运动很慢时,其 x 0, x 0,上式可简
5.初值定理
若L[f(t)]=F(s),则
f (0 ) lim f (t) lim s F(s)
t 0
s
6.终值定理
若L[f(t)]=F(s),则有
f () lim f (t) lim s F(s)
t
s0
7.延迟定理
若L[f(t)]=F(s),对任一正实数a,则有
L f (t a) f (t a)estdt eas F (s) 0
ic
1 C
dui dt
R C uo(t)
例5 写出下图电气系统的微分方程
R1 L1
L2
①
u(t)
i1( t ) C
i2 ( t ) uc( t )
R2
解:
u(t)
i1 R1
L1
di1 (t) dt
uc
(t)
(1)
uc (t)
L2
di2 (t) dt
i2 R2
(2)
uc
(t)
1 C
(i1 - i2 )dt
j0
i0
若系数ai,bi是常数,则方程是线性定常的,相应 的系统也称为线性定常系统,若系数是时间的函数, 则该方程为线性时变的,相应的系统也称为线性时变 系统。(m≥n)
机械工程控制基础课件 第2章: 系统的数学模型

控制系统的状态空间模型
要点一
总结词
控制系统的状态空间模型
要点二
详细描述
状态空间模型是一种描述控制系统动态行为的数学模型, 它通过建立系统的状态方程和输出方程来描述系统的动态 特性。在状态空间模型中,系统的状态变量、输入变量和 输出变量都被表示为矩阵和向量的形式,从而能够方便地 描述系统的动态行为。状态空间模型具有直观、易于分析 和设计等优点,因此在控制工程中得到了广泛应用。
传递函数模型的求解
通过求解传递函数模型中的代数方程或超 越方程,得到系统在给定输入下的输出响 应。
04
控制系统的数学模型
控制系统的定义与分类
总结词
控制系统的定义与分类
详细描述
控制系统的定义是:控制系统是一种能够实现自动控制和调节的装置或系统,它能够根 据输入信号的变化,自动调节输出信号,以实现某种特定的控制目标。控制系统可以分 为开环控制系统和闭环控制系统两类。开环控制系统是指系统中没有反馈环节的控制系
状态空间模型的求解
通过数值计算方法求解状态空间模型中的微分方程或差分方程,得到 系统状态变量的时间响应。
非线性系统的传递函数模型
总结词
传递函数模型的建立、性质和求解
传递函数模型的性质
传递函数模型是非线性的,具有频率响应 特性,可以描述系统在不同频率下的行为
特性。
传递函数模型的建立
通过拉普拉斯变换将非线性系统的微分方 程或差分方程转换为传递函数的形式,从 而建立非线性系统的传递函数模型。
03
非线性系统的数学模型
非线性系统的定义与性质
总结词
非线性系统的定义、性质和特点
非线性系统的定义
机械工程控制基础 华中科大第7版 第2章系统的数学模型

2.2 系统的微分方程
三、非线性微分方程的线性化
1. 非线性方程线性化的条件 1) 非线性函数是连续函数(即非线性不是本质非线性) 2) 系统在预定工作点附近作小偏差运动,即变量的变化
范围很小。 2. 非线性方程线性化的方法 1) 确定预定工作点; 2) 在工作点附近将非线性方程展开成泰勒级数形式; 3) 忽略高于一阶项; 4) 表示成增量方程的形式。
第二章 系统的数学模型
2.2 系统的微分方程
二、系统微分方程的列写
1. 机械系统
F ma
F ma 0
遵循的定律:牛顿第二定律或达朗贝尔原理
(1)直线运动
元素:质量m、弹簧k、粘性阻尼器c
质量元件:
F ma mx
阻尼元件: c Fc cv cx,c—粘性阻尼系数
4. 整理所得到的微分方程,将与输出有关的项放在方程
的左侧,与输入有关的项放在方程的右侧,各阶导数项
按降幂方式排列。 如: an x0(n) (t) an1x0(n1) (t) a1x0 (t) a0 x0 (t)
bm xi(m) (t) bm1x0(m1) (t) b1xi (t) b0 xi (t)
L
R
解:根据克希荷夫电压定律,得
u
i
C
u(t)
L
di(t dt
)
Ri
(t
)
1 C
i(t)dt
∵ i(t) dq(t)
dt
消去中间变量i(t),并整理得,
LCq(t) RCq(t) q(t) Cu(t)
第二章 系统的数学模型
2.2 系统的微分方程
机械控制工程课后习题解答
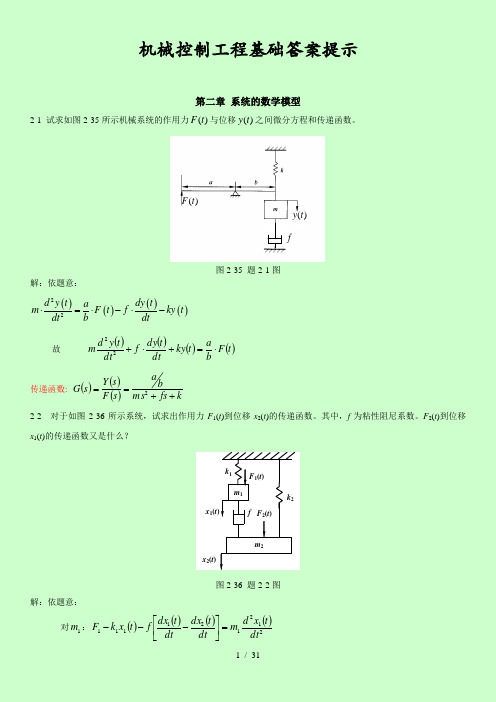
机械控制工程基础答案提示第二章 系统的数学模型2-1 试求如图2-35所示机械系统的作用力)(t F 与位移)(t y 之间微分方程和传递函数。
)(t F )(t y f图2-35 题2-1图解:依题意:()()()()22d y t dy t a m F t f ky t dt b dt ⋅=⋅-⋅-故 ()()()()t F b at ky dt t dy f dt t y d m ⋅=+⋅+22 传递函数: ()()()kfs m s b as F s Y s G ++==22-2 对于如图2-36所示系统,试求出作用力F 1(t )到位移x 2(t )的传递函数。
其中,f 为粘性阻尼系数。
F 2(t )到位移x 1(t )的传递函数又是什么?m 2m 1k 1 f k 2F 1(t )F 2(t ) x 2(t )x 1(t )图2-36 题2-2图解:依题意:对1m :()()()()212121111dt t x d m dt t dx dtt dx f t x k F =⎥⎦⎤⎢⎣⎡---对两边拉氏变换:()()()[]()s X s m s sX s sX f x k s F 12121111=---①对2m :()()()()()222222212dt t x d m t x k dt t dx dt t dx f t F =-⎥⎦⎤⎢⎣⎡-+ 对两边拉氏变换:()()()[]()()s X s m s x k s sx s sx f s F 22222212=--+②故: ()()()()()()()()⎩⎨⎧=+++-=-++S F s x k fs s m s fsx s F s fsx s x k fs s m 222221121121 故得:()()()()()()()()()()()()()()⎪⎪⎩⎪⎪⎨⎧-+++++++=-+++++++⋅=22221212212122222121222211fs k fs s m k fs s m k fs s m s F s fsF s x fs k fs s m k fs s m s fsF k fs s m s F s x 故求()t F 1到()t x 2的传递函数令:()02=s F()()()()()()()()()2122211122432121212211212x s fsG s F s m s fs k m s fs k fs fsm m s f m m s m k m k s f k k s k k ==++++-=+++++++求()t F 2到()t x 1的传递函数 令:()01=s F()()()()()()()()()1122221122432121212211212x s fsG s F s m s fs k m s fs k fs fsm m s f m m s m k m k s f k k s k k ==++++-=+++++++2-3 试求图2-37所示无源网络传递函数。
机电机械工程控制基础系统数学模型2名师公开课获奖课件百校联赛一等奖课件

0 Cd ua0 CmM L0
若某一时刻,输入量发生变化,其变化值为:ua ; M,电L 机旳平衡状态
被破坏,输出亦发生变化,其变化量为:,这时,输入量和输出量可表
示为增量形式:
ua ua0 ua , M L M L0 M L , 0
第二章 系统数学模型
TaTm
d 2 (0
dt 2
4、变换成原则形式。将与输入有关旳项写在微分方程旳右边, 与输出有关旳项写在微分方程旳左边,而且各阶导数项按降幂 排列。
第一节 系统微分方程 经典元件所遵照旳物理定律 机械系统:
质量元件:
第二章 系统数学模型
弹性元件:
阻尼元件:
第一节 系统微分方程
经典元件所遵照旳物理定律 电网络:
容性元件:u(t
)
Tm
d (0
dt
)
(0
)
Cd
(ua0
ua0 ) CmTa
d (M L0 M L ) dt
Cm (M L0
M L )
化简并整顿得:
TaTm
d
2 ()
dt 2
Tm
d ()
dt
(0
)
Cd
(ua0
ua0 )
CmTa
d (M L ) dt
Cm (M L0
M L )
考虑到 0 Cd ua0 CmM L0 于是有:
RC
duo (t) dt
uo (t)
ui (t)
第一节 系统微分方程
第二章 系统数学模型
微分方程举例:
例2-4:试列出如图所示电气系统旳微分方程。
1、明确系统旳输入和输出 输入为ui,输出为uo。
R1
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
kx f m
cx
f kx cx mx
3. 整理: mxcxkx f
f
k
m
c
x
例2:图示电网络,列写微分方程。 1. 明确系统的输入与输出:
输入u(t),输出电量q
2. 列写原始微分方程:
u
L
di dt
iR
C1
idt
u
i dq dt
3. 消除中间变量,并整理
.. Lq
Rq. C1
q
u
L
R
(1) 确定系统预定工作点 q0 q(x0 , p0 )
(2) 二元泰勒公式展开
q( x,
p)
q( x0 ,
p0 )
q x
x0, p0
x
q p
x0, p0
p
(3) 增量方程 4. 代入原方程
p
1 Kc
(Kqx q)
Kq Kc
x
A Kc
y'
my '' cy ' Ap
整理得
my '' (c A2 / Kc ) y ' ( AKq / Kc )x
R2C2
R1C2 )s
1
五、典型环节传递函数
系统传递函数往往是高阶的,高阶传递函数可化为比例、惯性、 积分、微分、振荡等低阶典型环节传递函数的组合
1. 比例环节 ——输出正比于输入
动力学方程: xo (t) Kxi (t)
Xi (s)
K
X o (s)
传递函数: G(s) K
特点:输出量与输入量成正比;不失真,不延迟。
例: R2
m
m
N 1
ui (t) R1
uo(t)
L
L
N 2
2. 惯性环节 ——输出的导数与输出之和正比于输入
动力学方程:
传递函数: 例1:
T
dxo (t) dt
xo (t)
Kxi
(t)
G(s) K Ts 1
例2:
k(xi xo ) cxo
cxo kxo kxi
G(s) 1 RCs 1
特点:
➢ 一般不能单独存在
➢ 增加阻尼;
➢ 强化噪声。
例1: 微分运算电路
i1 R1
i C dui 0 uo dt R1
第二章 系统的数学模型
2.1 系统的微分方程
一、引言
数学模型:描述系统动态特性的数学表达式 时域数学模型: 微分方程(连续系统)
差分方程(离散系统) 状态方程 复域数学模型: 传递函数(连续系统) Z传递函数(离散系统) 频域数学模型: 频率特性
数学建模的一般方法: 1.分析法: 根据系统或元件所遵循的有关定律来建模
(i1 i2 )dt u1
u1
C1
i2 C2 u2
i2R2
1 C2
i2dt
1 C1
(i1 i2 )dt
1
C2
i2dt u2
3.在零初始条件下,进行拉氏变换:
R1I1
I1 I2 C1s
U1
R2 I2
I2 C2s
I1 I2 C1s
I2 C2 s
U2
3.在零初始条件下,进行拉氏变换:
i
例3:列写微分方程
1. 明确:输入T,输出x(t)
2. 微分方程:
T k1( )
T k1
.. . f mx B xk x
0
2
2
k1(
)
J
B 1
rf
x r
3. 消除中间变量 f、q,并整理:
r
f m k2
..
.
(J mr2)x(B B r2)xk r2x rT
12
2
J B1
x
B2
例4:图示电网络,列写微分方程。
xo(t)3xo(t)7xo(t) 4xi(t)5xi(t)
x (t)3x (t)7x (t) 4t2x (t)5x (t)
o
o
o
i
i
线性定常系统 线性时变系统
x (t)3x x (t)7x (t) 4t2x (t)5x (t) 非线性系统
o
oo
o
i
i
线性系统的叠加原理
二、列写微分方程的一般方法
1. 明确系统的输入与输出:
R1
输入u1,输出u2
2. 列写微分方程: 1
u1
i1R1 C1 (i1 i2 )dt u1
i2R2
1 C2
i2dt
1 C1
(i1 i2 )dt
1
C2 i2dt u2
i1 C1
3. 消除中间变量 i1、i2,并整理:
R1C1R2C2
d2u2 dt 2
(R1C1
3. 在零初始条件下,当输入确定时,系统的输出完全取决于系 统的传递函数 xo (t) L1[ X o (s)] L1[G(s) X i (s)]
4.物理性质不同的系统,可以具有相同的传递函数(相似系统)
传递函数的零极点模型 G(s) K (s z1)(s z2 )...(s zm ) (s p1)(s p2 )...(s pn )
q
q
q( x, p) q( x0 , p0 ) x x0, p0 x p x0, p0 p
已略去高阶小量
例6 液压伺服机构
油池
高压油
油池
my '' cy ' Ap
阀芯
x
q Ay '
q f ( p, ) cd xx p / y
3. 非线性函数线性化:
q p1
q A
油缸 负载
p2
mc
G(s) Xo k 1 1 Xi cs k c s 1 Ts 1 k
特点: 存在储能元件和耗能元件。 阶跃输入时,输出经过一段时间才到稳态值。
3. 微分环节 ——输出正比于输入的变化率 动力学方程: xo (t) T xi (t)
Xi (s) Ts Xo (s)
传递函数: G(s) Ts
R1I1
I1 I2 C1s
U1
R2 I2
I2 C2s
I1 I2 C1s
I2 C2 s
U2
R1
i1
u1
C1
R2 i2 C2 u2
4.消除中间变量,并整理得:
[R1C1R2C2s2 (R1C1 R2C2 R1C2 )s 1]U2 U1
5.传递函数
G(s)
R1C1 R2C2 s 2
1 (R1C1
a s n1 n1
...
a1 s
a0
(n m) 传递函数
传递函数定义:
零初始条件下,线性定常系统输出的拉氏变换与输入的拉
氏变换之比。
传递函数特点:
传递函数方框
1.传递函数是关于复变量s的复变函数,为复域数学模型;
2.传递函数的分母反映系统本身与外界无关的固有特性, 传递 函数的分子反映系统与外界的联系;
2.实验法: 根据实验数据整理拟合数模
实验法列微分方程举例—OriginPro 8
实验法列微分方程举例—OriginPro 8
实验法列微分方程举例—OriginPro 8
连续系统的微分方程的一般形式:
an
x (n) o
(t
)
a n1
x ( n1) o
(t
)
...
a1
x o
(t
)
a0
xo
(t
)
...
b1 s
b0 ) X i (s)
X o (s)
bm s m
b s m1 m1
... b1s b0
Xi (s)
an s n
a s n1 n1
...
a1 s
a0
(n m) 系统与外界联系 系统固有特性
G(s)
X o (s)
bm s m
b s m1 m1
...
b1 s
b0
Xi (s)
an s n
R2C2
R1C2
)
du2 dt
u2
u1
R2 i2 C2 u2
例5 直流电动机
1. 明确输入与输出:
输入ua 和ML,输出
2. 列写原始微分方程: ua
L
dia dt
ia R
ed
ua
ed kd
d
J dt M M L
ua
M kmia
3.消除中间变量,并整理:
L
R
励磁电流
i2 =const
bm
x
( i
m
)
(
t
)
bm1
x
( i
m
1 )
(
t
)
...
b1 x i
(t )
b0
xi (t)
xo (t)、xi (t) 分别为系统输出和输入; ai (i 0,1,2,..., n)、 bj ( j 0,1,2,..., m) 为微分方程系数
若所有系数都不是输入、输出及其各阶导数的函数,则微 分方程表示的系统为线性系统;否则,系统为非线性系统。 对线性系统,若系数为常数则为线性定常系统。
线性化特点:
1. 非线性项线性化后微分方程是增量形式的微分方程。 2. 线性化的结果与系统的预定工作点有关。
如:本例中,不同预定点的kq、kc不同
3. 非线性项线性化必须满足连续性和小偏差条件。
三、相似系统
L
R
u
i
f
k
m
组成系统的 物理元件不同
c
x
.. Lq
