计量经济学 第二版 庞皓 第九章 设定误差与测量误差
(完整word版)《计量经济学》第二版-庞皓-试卷2

2009第一学期《计量经济学》试卷一、填空题(20%, 每空1分)1.计量经济学是以 为指导, 以 为依据, 以 为方法, 以计算机专用软件为手段, 研究经济关系和经济活动的 规律及其应用, 并以建立和应用经济数学模型为核心的一门经济学学科。
2、对于计量经济模型的检验的内容, 一般分为四种形式的检验: 、 、 和 。
3.在计量经济学中线性模型的“线性”有两种解释: 一是模型就 而言是线性的, 二是模型就 而言是线性的。
在计量经济学中, 从回归理论的发展和参数的估计方法考虑, 通常是就 而言来判断是否线性回归模型。
4.简单线性回归模型的五条基本假定是: (1) ;(2) ; (3) ;(4) ;(5) 。
5.根据高斯-马尔可夫定理, 最小二乘估计具有四个性质: (1) 、(2) 、(3) 、(4) 。
二、判断题(10%, 每题1分, 请将×或√写在表格中, 否则该题不得分。
) 1.( )经典线性回归模型 的零均值假设是指 。
2.( )对经济计量模型进行的各种检验中, 经济准则检验是第一位的, 如果经济准则检验无效, 则只能放弃模型。
3.( )如果可决系数r2等于0.8, 说明在总变差中有80%是可以由所拟合的回归直线作出解释的。
4.( )当估计标准误差s =0时, 说明被解释变量的观测值Yi 与回归估计值Ŷi 完全一致。
5.( )若X 与Y 为函数关系, 则相关系数| r|=1。
6、( )对于单个回归系数进行t -检验, 目的在于检验参数的估计量是否等于参数真值。
7、( )描述产品平均成本(Y )依存产品产量(X )而变动的关系, 适宜配合倒数变换模型 。
8、( )依据样本资料计算的相关系数r 是一个随机变量。
9、( )在使用横截面数据进行经济计量分析时, 要求指标统计的对象及其范围必须相同。
10、( )在经济计量研究中, 有时引入滞后内生变量作为解释变量, 作为解释变量的滞后内生变量是非随机变量。
计量经济学(庞皓_第二版)课后习题及答案(1)
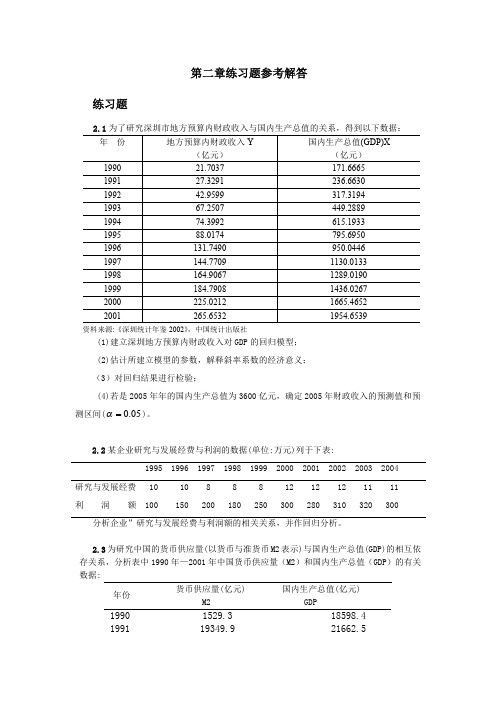
Yf 个别值置信度 95%的预测区间为:
∑ ^
^
Yf m tα 2 σ
1+ 1 + (X f − X )2
n
xi2
即
480.884 m 2.228× 7.5325× 1+ 1 + 7195337.357
12 3293728.494
= 480.884 m 30.3381 (亿元)
练习题 2.3 参考解答 计算中国货币供应量(以货币与准货币 M2 表示)与国内生产总值(GDP)的相关系数为
Yˆ2005 = −3.611151 + 0.134582 × 3600 = 480.884 (亿元)
区间预测:
∑ 平均值为:
xi2
=
σ
2 x
(n
−1)
=
587.26862
× (12
−1)
=
3793728.494
( X f 1 − X )2 = (3600 − 917.5874)2 = 7195337.357
测区间(α = 0.05 )。
2.2 某企业研究与发展经费与利润的数据(单位:万元)列于下表: 1995 1996 1997 1998 1999 2000 2001 2002 2003 2004
研究与发展经费 10 10 8 8 8 12 12 12 11 11 利 润 额 100 150 200 180 250 300 280 310 320 300
Yˆi = 6.017832 − 0.070414 × 80 = 0.384712 (次)
练习题 2.7 参考解答
美国软饮料公司的广告费用 X 与销售数量 Y 的散点图为
说明美国软饮料公司的广告费用 X 与销售数量 Y 正线性相关,可建立线性回归模型
计量经济学复习提纲—庞皓版

第一章1.计量分析的四个步骤:模型设定——参数估计——模型检验——模型应用2.计量模型检验:经济意义检验——统计推断检验——计量经济学检验——模型预测检验3.计量模型的应用:结构分析——经济预测——政策评价——检验与发展经济理论4.正确选择解释变量的原则:符合理论、规律——忽略众多次要因素,突出主要经济变量——数据可得性——每个解释变量之间是独立的5.参数的数据类型:时间序列数据——截面数据——面板数据——虚拟变量数据第二章1.总体相关系数:ρ=Cov(X,Y)/√Var(X)√Var(Y)2.样本相关系数:rxy=Σ(Xi-X_)(Yi-Y_)/√Σ(Xi-X_)^2√Σ(Yi-Y_)^23.总体回归函数中引入随机扰动项的原因:作为未知影响因素的代表——作为无法取得数据的已知因素代表——作为众多细小影响因素的综合代表——模型的设定误差——变量的观测误差——经济现象的内在随机性4.简单线性回归模型的基本假定:1、对变量和模型的假定;2、对随机扰动项ui统计分布的假定(古典假定):零均值假定——同方差假定——无自相关假定——随机扰动项ui与解释变量Xi不相关——正态性假定5.违反零均值假定:影响截距上的估计(影响小)6.违反正态性假定:不影响OLS估计是最佳无偏性,但会使t检验F检验失真(影响大)7.样本回归函数的离差形式:yi^=β2^*xi8.OLS估计值的离差表达式:β2^=Σ(Xi-X_)(Yi-Y_)/Σ(Xi-X_)^2=Σxiyi/Σxi^2β1^=Y_-β2^*X_9.OLS回归线的性质:样本回归线过(X_,Y_)——估计值均值等于实际值均值——剩余项ei的均值为零——Cov(Yi^,ei)=0——Cov(Xi,ei)=010.β^的评价标准:无偏性——有效性——一致性11.β^的统计性质:线性——无偏性——有效性12.Var(^β1)=Ơ^2/Σxi^2——Var(^β2)=ΣXi^2/n*Ơ^2/Σxi^213.^Ơ^2=Σei^2/(n-2)14.总变差平方和:Σ(Yi-Y_)^2=Σyi^2……TSS……n-1回归平方和:Σ(Yi^-Y_)^2=Σ^yi^2……ESS……k-1残差平方和:Σ(Yi-Yi^)^2=Σei^2……RSS……n-k15.可决系数:R^2=ESS/TSS16.SE(^β1)=√(Ơ^2ΣXi^2)/(nΣxi^2)SE(^β2)=√Ơ^2/Σxi^217.t=(^β1-β1)/^SE(^β1)~t(n-2)t=(^β2-β2)/^SE(^β2)~t(n-2)18.区间估计:1.当总体方差Ơ^2已知,α=0.1—±1.645,α=0.05—±1.96,α=0.01—±2.33,P[-tα<z=(^β2-β2)/^SE(^β2)<tα]=1-α2.当总体方差Ơ^2未知,样本容量大,可用^Ơ^2=Σei^2/(n-2)代替Ơ^2,z=(^β2-β2)/(^Ơ/√Σxi^2)3.当总体方差Ơ^2未知,样本容量小,P[-tα/2<t=(^β2-β2)/^SE(^β2)<tα/2]=1-α19.对Y平均值的区间预测:SE(^Yf)=Ơ√{1/n+[(Xf-X_)^2/Σxi^2]},置信度1-α的预测区间[^Yf-tα/2*SE(^Yf),^Yf+tα/2*SE(^Yf)]20.对Y个别值预测区间:Yf=^Yf±tα/2*^Ơ√{1+1/n+[(Xf-X_)^2/Σxi^2]}第三章1.多元线性回归模型的古典假定:零均值假定——同方差和无自相关假定——随机扰动项与解释变量不相关——无多重共线性假定——正态性假定2.修正的可决系数:_R^2=1-(1-R^2)(n-1)/(n-k)……k是待估参数个数,R^2必定为正,但修正的可决系数可能为负,这是规定其为0,随着k的增加,_R^2越来越小于R^23.F=ESS(k-1)/RSS(n-k)=R^2/(1-R^2)*(n-k)/(k-1)4.S.E.of regression:Ơ^2=Σei^2/(n-k)——Ơ=5.t-statistic=coefficient/std.error6.TSS=(n-1)*(S.D.dependent var)^2第四章1.多重共线性产生的原因:经济变量之间具有共同变化趋势——模型中包含滞后变量——利用截面数据建立模型也可能出现多重共线性——样本数据自身的原因2.完全多重共线性产生的后果:参数的估计值不确定——参数估计值得方差无限大3.不完全多重共线性后果:参数估计值的方差和协方差增大——对参数区间估计时,置信区间趋于变大——严重多重共线性时,假设检验容易作出错误判断——参数估计经济含义不合理。
计量经济学课件(庞浩版)

劳动经济学中经常运用联立方程模型来研究劳动力市场中 的各种问题,如工资决定、就业与失业、劳动力流动等。 例如,可以构建一个包含工资方程和就业方程的联立方程 模型,以分析最低工资制度对就业和工资水平的影响。
06
CATALOGUE
面板数据计量经济学模型
面板数据基本概念与特点
面板数据定义
面板数据是指在时间序列上取多个截面,在这些截面上同时选取样本观测值所构成的样 本数据。
面板数据模型估计方法及应用举例
估计方法
面板数据模型的估计方法主要有最小二乘法 、广义最小二乘法和极大似然法等。
应用举例
面板数据模型在经济学、金融学、社会学等 领域有广泛的应用,如经济增长、劳动力市 场、金融市场、环境经济学等问题的研究。 例如,可以利用面板数据模型研究不同国家 经济增长的影响因素,或者分析某个政策对 不同地区或不同群体的影响效果。
模型设定
多元线性回归模型是描述多个自变量与一 个因变量之间线性关系的模型,形式为 Y=β0+β1X1+β2X2+...+βkXk+u。
假设ห้องสมุดไป่ตู้验
对各个自变量的回归系数进行假设检验, 判断其是否显著不为零。
参数估计
通过最小二乘法等方法对模型中的参数进 行估计,得到各个自变量的回归系数估计 值。
多重共线性问题
采用逐步回归法、岭回归法、主成分分析法等方法对多重 共线性进行修正,同时也可以通过增加样本容量或收集更 多信息来缓解多重共线性的影响。
04
CATALOGUE
时间序列计量经济学模型
时间序列基本概念与性质
时间序列定义
按时间顺序排列的一组数据,反映现象随时间 变化的发展过程。
计量经济学-(西南财大)庞皓-博导

●计量经济学对经济关系要作出定量的估计,
对经济理论提出经验的内容
18
2、计量经济学与经济统计学的关系
联系:
●经济统计侧重于对社会经济现象的描述性计量
●经济统计提供的数据是计量经济学据以估计参
数、验证经济理论的基本依据
●经济现象不能作实验,只能被动地观测客观经 济现象变动的既成事实,只能依赖于经济统计 数据
假定条件经常不能满足,需要建立一些专门的
经济计量方法
21
第二节 计量经济学的研究方法
需要做的工作
选择变量和数学关系式 —— 模型设定
确定变量间的数量关系 —— 估计参数
检验所得结论的可靠性 —— 模型检验
作经济分析和经济预测 —— 模型应用
22
一、模型设定
经济模型及设定
模型:对经济现象或过程的一种数学模拟 设定(Specification):
数据的要求:
真实性、完整性、可比性
37
四、计量经济模型的建立
经济模型是对实际经济现象或过程的一种数学模
拟,是对复杂经济现象的简化与抽象 特点:只能在一定假定前提下 忽略次要因素,突出主要因素
38
可利用来建立计量经济模型的关系:
行为关系(如生产、投资、消费)
生产技术关系 (如投入产出关系)
制度关系(如税率) 定义关系 计量经济模型的数学形式: 线性模型:如 非线性模型:如
8
特点
计量经济学的重要特点是它自身并没有固定的 经济理论,计量经济学中的各种计量方法和技 术,大多来自数学和统计学。
计量经济学产生的意义
从定性研究到定量分析的发展,是经济学更精 密、更科学的表现,是现代经济学的重要特征
计量经济学西南财大庞皓博导

●理论与方法的新突破
除了经典线性计量经济学模型以外,出现 非线 性模型、合理预期模型、非参数、半参数模型、 动态模型、时间序列模型、协整理论、Panel Data数据模型、贝叶斯方法、小样本理论等 新的研究领域
11
二、计量经济学的性质
若干代表性表述:
●“计量经济学是统计学、经济学和数学的结合。” (弗瑞希)
13
注意:计量经济研究的三个方面
理论:即说明所研究对象经济行为的经济理论 ——计量经济研究的基础
数据:对所研究对象经济行为观测所得到的信息 ——计量经济研究的原料或依据
方法:模型的方法与估计、检验、分析的方法 ——计量经济研究的工具与手段
三者缺一不可
14
计量经济学研究的基本概述:
经济 数量化 经济
表现经济变量相互依存程度的、决定经济结 构和特征的、相对稳定的因素,通常不能直 接观测。
24
设定计量经济模型的基本要求
●要有科学的理论依据 ●选择适当的数学形式
类型: 单一方程、联立方程 线性形式、非线性形式
● 模型要兼顾真实性和实用性
两种不好的模型: 太过复杂—真实但不实用 过分简单—不真实
● 包含随机误差项
●“计量经济学是用数学语言来表达经济理论,以便通 过统计方法来论述这些理论的一门经济学分支。” (美国现代经济词典)
●“计量经济学可定义为:根据理论和观测的事实,运 用合适的推理方法使之联系起来同时推导,对实际经 济现象进行的数量分析。” (萨谬尔逊等)
各种表述的共性:
计量经济学与经济理论、统计学、数学都有关系
43
第二章 简单线性回归模型
本章主要讨论:
●回归分析与回归函数 ●简单线性回归模型参数的估计 ●拟合优度的度量 ●回归系数的区间估计和假设检验 ●回归模型预测
计量经济学-设定误差与测量误差

设正确的模型为:
Yi 1 2 X 2i 3i X 3i ui
正确模型离差形式为:
yi 2 x2i 2 x3i (ui - u )
15
却对方程 Yi 1 2 X 2i i 进行回归,得: 取期望
计量经济学
第 九 章 设定误差与测量误差
1
引子:简单一定胜于复杂吗?
西方国家盛行奥卡姆剃刀(Occam`s razor)原则,威廉修士称原理为“如 无必要,勿增实体”(意思是“简单优于复杂”的节约性原则)。这一原 理最常见的形式是:如果你有两个原理,它们都能解释观测到的事实, 那么你应该使用简单的那个,直到发现更多的证据。(经济原理、吝啬 定律、朴素原则)。经济模型永远无法完全把握现实,在建立模型中一 定的抽象和简化是不可避免的。 在研究进口与国内生产总值的关系时,考虑到时间趋势,建立并估计了 以下模型
对模型的设定是计量经济研究的重要环节。 前面各章除了对随机扰动项 ui 分布的基本假定以 外,还强调:
假定设定的模型对变量和函数形式的设定是
正确地描述被解释变量与解释变量之间的真实关
系,假定模型中的变量没有测量误差。
但是在实际的建模实践中,对模型的设定不一定
能够完全满足这样的要求,从而会使模型出现设
10
1. 相关变量的遗漏
(Omitting Relevant Variables)
例如,如果“正确”的模型为
Yi 1 2 X 2i 3 X 3i i
而我们将模型设定为
Yi 1 2 X 2i i
即设定模型时漏掉了一个相关的解释变量。 这类错误称为遗漏相关变量(“欠拟合”)。
第九章_设定误差

DW检验步骤如下: 1、对设定的回归模型运用OLS估计得残差序列 ei ; 2、假设 H0:未遗漏相关变量,H1:遗漏相关变量 ; 3、计算DW统计量: n 2 ( e e ) i i 1 DW i 2 n 2 e i
i 1
4、查DW表,得临界值dL和dU,进行判断,如 果DW值显著,则拒绝原假设,表明遗漏了 重要的解释变量,否则,表明没有遗漏。
变量设定误差主要有两类: 相关变量的遗漏(欠拟合) 无关变量的误选(过拟合)
9
1、遗漏相关变量(欠拟合)的后果
把采用遗漏了重要解释变量的模型进行估计而带 来的偏误,称为遗漏相关变量误差。
假定真实模型为: Yi =β1 +β2 X2i +β3X3i + ui 但因某种原因遗漏了解释变量 X3,而将模型设为:
Yi X i ei ui X i vi
为使问题简化,假定
2 e ~ N ( 0 , ui ~ N (0, ), i e )
(2)
2 u
且 ui 和 ei 是不相关的,于是
var( ui ei )
2 v 2 u
2 e
因此,如果用OLS分别估计(1)和(2)式,得
25
一、测量误差的后果
1、被解释变量的测量误差 设真实的模型为
Yi X i u i
*
(1)
其中Yi* 为被解释变量的理论值,Xi为解释变量的理 论值。 假设由于某种原因,被解释变量的观测值 Yi 与理论 值之间存在一个测量误差 ei ,即
Yi Yi* ei
26
于是上述模型相应变为
Yi =α1 +α2X2i + vi
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设定误差的原因
●数据来源渠道可能不畅。例如,数据很难取得被 数据来源渠道可能不畅。例如, 迫将具有重要的经济意义变量排斥在模型之外。 迫将具有重要的经济意义变量排斥在模型之外。 ●不知道变量应当以什么确切的函数形式出现在回 归模型中。 归模型中。 ●事先并不知道所研究的实证数据中所隐含的真实 模型究竟是什么。 模型究竟是什么。 设定误差在建模中较容易出现。 设定误差在建模中较容易出现。设定误差的存在 可能会对模型形成不良的后果。 可能会对模型形成不良的后果。
σ2
ˆ Var(β2 ) =
∑ x2i x3i ) 2 ∑ x2i (1- x2 x2 ∑ 2i ∑ 3i
σ2
=
2 2 x2i (1- r23 ) ∑
σ2
17
ˆ 相关, ˆ 如果 X 3 与 X 2 相关,显然有 Var(α 2 ) ≠ Var( β 2 )
ˆ 不相关, 如果 X 3与 X 2不相关,也有 Var(α2 ) ≠ Var(β2 ) ˆ
yi = β2 x2i + β2 x3i + (ui - u )
13
却对方程 Y i = α 1 + α 2 X 进行回归, 进行回归,得:
ˆ α 2 = β 2 + β3
2i
+ν i
取期望
∑x x ∑x
2 i 3i 2 2i
∑ x (u - u ) + ∑x
2i i 2 2i
∑ x2i x3i + ∑ x2i (ui - u ) ˆ E (α 2 ) = E β 2 + β 3 2 2 ∑ x2i ∑ x2i
本下有偏,在大样本下非一致。 本下有偏,在大样本下非一致。
的估计却是有偏的。 性;但这时α2 的估计却是有偏的。 即OLS估计量在小样 估计量在小样
16
ˆ 方差的有偏估计: 3. α 2 的方差是 β 2 方差的有偏估计: ˆ
由Y
ˆ = β1 + β2X2 + β3X3 +u 得 Var(α2 ) = x2 ∑ 2i 由Y = α + α x + v 得 1 2 2
4
第九章 设定误差与测量误差
本章主要讨论: 本章主要讨论:
●设定误差 ●设定误差的检验 ●测量误差
5
第一节 设定误差
本节基本内容: 本节基本内容:
●设定误差及类型 ●变量设定误差的后果
6
一、设定误差及类型
计量经济模型是对变量间经济关系因果性的设想, 计量经济模型是对变量间经济关系因果性的设想, 若所设定的回归模型是“正确” 若所设定的回归模型是“正确”的,主要任务是所 选模型参数的估计和假设检验。 选模型参数的估计和假设检验。但是如果对计量模 型的各种诊断或检验总不能令人满意, 型的各种诊断或检验总不能令人满意,这时应把注 意力集中到模型的设定方面: 意力集中到模型的设定方面: 考虑所建模型是否遗漏了重要的变量? 考虑所建模型是否遗漏了重要的变量? 是否包含了多余的变量? 是否包含了多余的变量? 所选模型的函数形式是否正确? 所选模型的函数形式是否正确? 随机扰动项的设定是否合理? 随机扰动项的设定是否合理? 变量的数据收集是否有误差? 变量的数据收集是否有误差? 所有这些,计量经济学中被统称为设定误差。 所有这些,计量经济学中被统称为设定误差。 7
而我们将模型设定为
Y =α +α2 X2i +νi i 1
即设定模型时漏掉了一个相关的解释变量。 即设定模型时漏掉了一个相关的解释变量。 这类错误称为遗漏相关变量 遗漏相关变量( 欠拟合” 这类错误称为遗漏相关变量(“欠拟合”)。
9
2. 无关变量的误选
(Including Irrevelant Variables)
设定误差的类型
从误差来源看,设定误差主要包括: 从误差来源看,设定误差主要包括: (1)变量的设定误差,包括相关变量的遗漏 )变量的设定误差, 欠拟合)、无关变量的误选(过拟合); )、无关变量的误选 (欠拟合)、无关变量的误选(过拟合); (2)变量数据的测量误差; )变量数据的测量误差; (3)模型函数形式的设定误差; )模型函数形式的设定误差; (4)随机扰动项设定误差。 )随机扰动项设定误差。 本章主要讨论的两类变量设定误差: 本章主要讨论的两类变量设定误差
IM = -172.42 + 0.271 D - 949.12 + 160.73 2 - 10.18T3 G P T T
t = (-0.177) (5.67) (-2.22) (2.20) (-2.74)
R2 = 0.991 F = 272.95 D = 1.97 W
2
有人根据“简单优于复杂”原则,得到以下方程: 有人根据“简单优于复杂”原则,得到以下方程:
4. 遗漏变量 X 3 ,式中的随机扰动项 v i的方差估计 量将是有偏的, 量将是有偏的,即: ˆ σ v2 = RSSv ( n - 2)
ˆ E (σ v2 ) ≠ σ u2
5. 与方差相关的检验,包括假设检验、区间估计, 与方差相关的检验,包括假设检验、区间估计, 在关于参数的统计显著性方面, 在关于参数的统计显著性方面,都容易导出错误的 结论。 结论。
21
2. 包含无关变量偏误
定义:模型中包括了不重要的解释变量, 定义 模型中包括了不重要的解释变量,即采用误 模型中包括了不重要的解释变量 选了无关解释变量的模型进行估计而带来的偏误, 选了无关解释变量的模型进行估计而带来的偏误, 称为包含无关变量偏误 设正确模型 Y = β + β X + µ (1) 1 2 2 但却估计了 Y = α + α X + α X + v (2) 1 2 2 3 3 相同, 如果 α3 = 0 则(2)与(1)相同,因此,可将 式 , 与 相同 因此,可将(1)式 为约束的(2)式的特殊形式。 视为以 α3 = 0 为约束的 式的特殊形式。 采用OLS 法对(2)进行估计,有: 法对( )进行估计, 采用
18
ˆ ˆ (1) 若 X3与 2相关, 23 ≠ 0,显然,Var (α2 ) ≠ Var β2 X r2
ˆ ˆ 似乎有:Var (α2 ) < Var β2 ;
但实际情形并不完全如此。 但实际情形并不完全如此。 可以注意到残差平方和 可以注意到残差平方和RSS的计算 的计算
( )
( )
ˆ ˆ σν2 = RSSv (n − 2) ≠ RSSu (n − 3) = σu2 ;
例如,如果“真实模型” 例如,如果“真实模型”为:
Y = β1 + β2 X2i + β3X3i + µi i
但我们却将模型设定为
Y =α1 +α2 X2i +α3X3i +α4 X4i +νi i
即设定模型时,多选了一个无关解释变量。 即设定模型时,多选了一个无关解释变量。这类 错误称为无关变量的误选( 过拟合” 错误称为无关变量的误选(“过拟合”)。
11
二、变量设定误差的后果
当模型设定出现误差时, 当模型设定出现误差时,模型估计结果也会与 “实际”有偏误; 实际”有偏误; 偏误的性质与程度与模型设定误差的类型密切相 关。 从实质上看,变量设定误差的主要后果, 从实质上看,变量设定误差的主要后果,是一个 或多个解释变量与随机扰动项之间存在着相关性, 或多个解释变量与随机扰动项之间存在着相关性, 进而影响参数估计的统计特性。 进而影响参数估计的统计特性。
因此,有可能: 因此,有可能:
RSSv (n − 2) > RSSu (n − 3);
19
不相关, (2)若 X 3与X 2 不相关,有 )
2 r23 = 0和 ∑ x2i x3i 2 x2i = 0; ∑
似乎分别有: 似乎分别有: ˆ E (α2 ) = β2
ˆ ˆ Var(β2 ) = Var(α2 );
IM = -217.186 + 0.173G P D
t = (-0.5) ( 16.94)
(2)
R2 = 0.960 F = 286.95
D = 0.735 W
进行比较: 进行比较:
两个方程的检验结果都较理想; 两个方程的检验结果都较理想; 方程( ) 检验值似乎优于方程( ); 方程(2)GDP的t检验值似乎优于方程(1); 的 检验值似乎优于方程 方程( )函数形式也更为简单; 方程(2)函数形式也更为简单; 然而,能否根据“ 原则, 然而,能否根据“Occam’s razor”原则,判断方程(2)比 原则 判断方程( ) 方程( ) 方程(1)好?
3
对模型的设定是计量经济研究的重要环节。 对模型的设定是计量经济研究的重要环节。 前面各章除了对随机扰动项 还强调: 外,还强调 分布的基本假定以 ui
假定设定的模型对变量和函数形式的设定是 正确地描述被解释变量与解释变量之间的真实关 假定模型中的变量没有测量误差。 系,假定模型中的变量没有测量误差。 但是在实际的建模实践中, 但是在实际的建模实践中,对模型的设定不一定 能够完全满足这样的要求, 能够完全满足这样的要求,从而会使模型出现设 定误差。 定误差。
14
遗漏变量设定误差的后果
由此可以看出, 的遗漏将产生如下后果。 由此可以看出,X3的遗漏将产生如下后果。 两边取概率极限, 两边取概率极限,有:
Cov ( X 2i , X3i ) Cov ( X 2i , ui ) ˆ p limα2 = β2 + β3 + Var ( X 2i ) Var ( X 2i ) n→∞
(1)相关变量的遗漏(欠拟合); )相关变量的遗漏(欠拟合); (2)无关变量的误选(过拟合)。 )无关变量的误选(过拟合)。
8
1. 相关变量的遗漏
(Omitting Relevant Variables) )
