薄膜力学-3-生长模式
薄膜的生长过程和薄膜结构

薄膜生长过程概述
(2)表面扩散迁移 吸附气相原子在基体表面上扩散迁移,互相碰 撞结合成原子对或小原子团,并凝结在基体表面上。 (3)原子凝结形成临界核 这种原子团和其他吸附原子碰撞结合 ,或者释放一个单原子。这个过程反复进行,一旦原子团中的原 子数超过某一个临界值,原子团进一步与其他吸附原子碰撞结合 ,只向着长大方向发展形成稳定的原子团。含有临界值原子数的 原子团称为临界核,稳定的原子团称为稳定核。 (4)稳定核捕获其他原子生长 稳定核再捕获其他吸附原子,或者 与入射气相原子相结合使它进一步长大成为小岛。
(5-16)
式中,第一项正是自发形核过程的临界自由能变化(式5-5),
而后一项则为非自发形核相对于自发形核过程能量势垒降低的因
子。接触角θ越小,即衬底与薄膜的浸润性越好,则非自发形核
的能垒降低得越多,非自发形核的倾向也越大。在层状模式时,
形核势垒高度等于零。
薄膜的非自发形核理论
2、薄膜的形核率
形核率是在单位面积上,单位时间内形成的临界核心数目。为
10可求出形核自由能取得极值的条件为:
r* 2(a3 vf a2 fs a2 sv )
3a1GV
(5-14)
应用式5-11后,上式仍等于式5-4,即
r* 2 vf
GV
因而,虽然非自发形核过程的核心形状与自发形核时有所不同,
但二者所对应的临界核心半径相同。
将上式代入5-10得到相应过程的临界自由能变化为:
根据图5.5中表面能之间的平衡条件,核心形状的稳定性要求各
界面能之间满足关系式
sv fs vf cos
(5-11)
即θ取决于各界面之间的数量关系。薄膜与衬底的浸润性越差,
薄膜生长

薄膜生长与薄膜结构1、概述“薄膜”很难用一句话来定义。
为了与厚膜相区别,一般认为厚度小于1μm的膜称为薄膜。
另外针对于薄膜的生长过程和形态,人们对于薄膜的认知也不同,比如在成膜初期的岛状不连续构造,很多人不认为是薄膜。
薄膜(film)材料和块体(bulk)材料有很多的不同。
首先薄膜生长伴随着温度的急剧变化,内部会存在大量的缺陷;其次,薄膜的厚度与表面尺寸相比相差甚远,可以看成二维结构,表面效应非常强。
薄膜的最终性能与薄膜的生长过程密切相关。
从微观角度看,入射到基板或薄膜表面的气相原子,一部分被反射回去,一部分被表面捕获吸附后吸收能量再蒸发出去,一部分被表面捕获吸附后凝结成核,逐渐长大,最终形成连续的膜层。
下面将详细分析薄膜的生长过程。
2、吸附材料表面是一种特殊的状态,从结构方面讲,这里存在原子或分子间结合键的中断,因此具有吸引外来原子或分子的能力;从能量方面来讲,这里具有一种较高的能量:表面自由能,只有吸附了气相原子之后,自由能才会减小,从而变得稳定。
这种气相原子被吸引住的现象称为吸附,伴随吸附现象的发生而释放的能量称为吸附能。
入射到基板表面的原子可能会发生三种现象:1、与基板表面进行能量交换被吸附;2、吸附后在基板表面做短暂停留,能量过大或吸收能量后再次蒸发;3、直接被基板表面反弹回去。
用溅射法制备薄膜时,入射到基板表面的气相原子,绝大多数都与基板表面原子进行能量交换而被吸附。
如果吸附仅仅是由原子电偶极矩间的范德华力起作用,则称为物理吸附,比如冬天窗户上形成的雾状水气;如果吸附是由化学键结合力起作用,则称为化学吸附,比如当前研究比较热的纳米氧化层。
作为实际问题,使用何种材料,进行什么处理,在真空容器内发生哪种吸附,效果怎么样,这些还不能简单说清楚,特别是表面状态不能保持一定,越发使问题复杂化。
到现在为止,这方面的研究还不多。
在薄膜制造中,如果我们想要获得新材料,那么可以积极利用这种吸附情况;如果我们想得到清洁的纯膜,那么这种吸附会引起麻烦。
薄膜生长过程

Eε ≥ Ed
2G f [(1 +ν ) /(1 ν )]d c f 2 = [G f Gs /(G f + Gs )][b 2 / π (1 +ν )][ln(d c / b) + 1] / S
4,位错与薄膜生长间的关系: ,位错与薄膜生长间的关系:
a,Frank-Read位错与薄膜生长间的关系——低饱和蒸气压下薄膜生长
}
为薄膜的两种基本生长模式。
3,薄膜中的晶体缺陷: ,薄膜中的晶体缺陷:
其中(c)服从所谓的 Vegards law:
a(Ax B = (1 x)a A + xa B )
(b)称为肖特基缺陷; (a)称为弗兰克尔缺陷。
3,薄膜中的晶体缺陷: ,薄膜中的晶体缺陷:
→
螺位错
刃位错
层错与分位错有关,小角(大角)晶界与刃位错有关。
薄 膜 生 长 过 程
1,真空度对薄膜生长的影响: ,真空度对薄膜生长的影响:
J=nv
Pim JX = 2πm k BT
(JX为沿X方向的入射粒子流通量。)
2,表面能(表面张力ε与表面能 的关系): ,表面能(表面张力 与表面能 的关系): 与表面能γ的关系
产生新的表面,需要破坏一定数量的化学键。因此是吸热过 程,体系能量上升。所以表面能符号应为“+”!
衬底温度 * :1,薄膜 衬底 2,
11,薄膜生长:衬底对薄膜生长的影响 ,薄膜生长:
薄膜 B A B A B A B A 衬底
A B A B A B A B
B A B A B A B A
B A B A B A B A
B A B A B A B A Nhomakorabea举例:衬底缺陷(层错(等等))必然对薄膜生长有影响。
薄膜生长与制备技术简介

薄膜生长与制备技术简介一薄膜生长薄膜的生长过程直接影响薄膜的结构以及它的最终性能。
像其他材料的相变一样,薄膜的生长过程也可以划分为两个不同的阶段,即新相的成核与薄膜的生长过程。
1 薄膜气相成核1.1 成核的毛细作用理论这个理论模型是基于热力学概念,利用宏观物理量来讨论成核问题。
这个模型的优点是比较直观,一些物理量容易测量,理论计算和实验结构能直接进行比较。
由于采用宏观物理量,所以对原子数量较多的例子是适用的,而对原子团所含有原子数量少的情况,一些宏观物理参量的含义是不明确的。
1.1.1 自发形核理论自发成核,指的是整个成核过程完全是原子由气相转变为固相或液相的相变自由能推动下形成,也称为均匀成核。
在薄膜与衬底之间浸润性较差的情况下,薄膜的形核过程可以近似地认为是一个自发形核过程。
单位体积的固相在凝结过程中的相变自由能之差:(1)式中,P V和P分别是固相的平衡蒸气压和气相实际的过饱和蒸气压, Ω是原子体积,S是气相的过饱和度;M V和M分别是凝结相的蒸发通量和气相的沉积通量。
当气相存在过饱和现象时,∆G v<0,它就是新相形核的驱动力。
图1 自发形核过程示意图1.1.2非自发形核理论自发成核一般只发生在一些精心控制的过程之中。
在大多数相变过程中,成核的过程除了有相变自由能作推动力之外,还有其他的因素起着帮助新相核心生成的作用,即所谓成核的过程是非自发的。
新相的核心将首先出现在哪些能量比较有利的位置上。
假设在成核过程中,衬底表面的原子可以进行充分的扩散,即其扩散距离远大于原子的间距。
这时形成一个原子团时的自由能变化为:(2)式中,∆G v是单位体积的相变自由能,是薄膜成核的驱动力;γvf、γfs、γsv分别是气相(v)、衬底(s)与薄膜(f)三者之间的界面能。
而a1、a2、a3是与核心具体形状有关的三个常数。
图2 薄膜非自发形核核心的示意图1.1.3 薄膜的成核速率成核速率强烈地依赖与过饱和度。
薄膜形成过程和生长模式
薄膜的形成——薄膜形成过程和生长模式
0 cos 1 2 0
岛的形成又可以用另一热力 学变量描述:吸附能 界面结合能(粘附功)是指 原子团(核)吸附前后体系总的 自由能变化,即 Ecom
Ecom 2 0 1 0 ( 2 1 ) 0 0 cos 0 (1 cos )
薄膜的形成——溅射薄膜的形成过程
★ 溅射薄膜的形成过程
关于溅射薄膜形成过程的特点和溅射薄膜形成与生
长问题,在第三章已讨论。 真空蒸发薄膜和溅射薄膜形成物理过程的不同点:
沉积粒子产生过程 沉积粒子迁移过程
成膜过程
薄膜的形成——薄膜的外延生长
★ 薄膜的外延生长
外延的概念 同质外延 异质外延 失配度
薄膜的形成——薄膜形成过程和生长模式
沟道阶段 孤立的岛有变圆的趋势。当岛结合以后,在岛的生
长过程中变圆趋势减小,岛被拉长,连接网状结构,其 中分布着宽度为5-20nm的沟道。 随着沉积,在沟道中会发生二次或三次成核。
连续薄膜阶段
当沟道和孔洞消除后,入射到基片表面上的原子直 接吸附在薄膜上,形成连续薄膜。
薄膜的形成——薄膜形成过程和生长模式
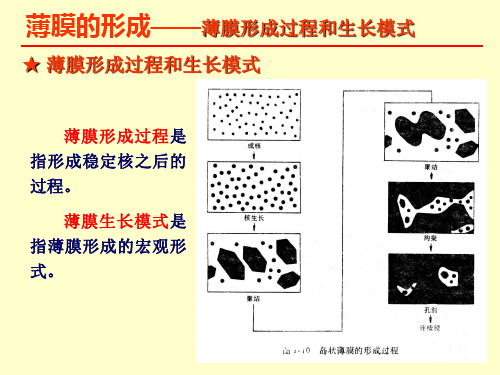
薄膜形成可划分为四个阶段:成核、结合、沟道、连续 岛状阶段 岛的演变特点 可观察到的最小核尺寸:2-3nm; 核进一步长大变成小岛,横向生长速度大于纵向 生长速度; 形状:球帽形——原形以用热力学变量描述:表面自由能
薄膜的形成——薄膜形成过程和生长模式
★ 薄膜形成过程和生长模式
薄膜形成过程是 指形成稳定核之后的
过程。
薄膜生长模式是 指薄膜形成的宏观形 式。
薄膜的形成——薄膜形成过程和生长模式
薄膜生长机理

b) 联并阶段 随着岛不断长大,岛间距离逐渐减小,最后相邻小岛 可互相联结合并为一个大岛。这就是岛的联并。联并 过程小岛的变化如图所示。小岛联并长大后,基体表 面上占据面积减小,表面能降低,基体表面上空出的 地方可再次成核。岛的联并与固相烧结相类似。
基体温度对岛的联并起着重要作用。
在联并时,传质的可能机理是体扩散和表面扩散,其 中主要的是表面扩散,核越小时,越是如此。因为已 经观察到在短至0.06s时间以内,就可在岛间形成相当 线度的颈部(岛间结合部),这可用表面扩散给以满 意的解释。 虽然小岛联并的初始阶段很快,但在长时间内,新岛 继续改变它的形状。所以在联并时和联并后,岛的面 积不断发生着改变。在最初几秒内,由于联并使基体 表面上的覆盖面积减小,而后又逐渐增大。在联并之 初,为了降低表面自由能,新岛的面积减小、高度增 大。 根据基体、小岛的表面与界面自由能,小岛有一最低 能量沟形,该形状有一定高度与半径比。
2. 沉积离子的迁移过程
在真空蒸发时其真空度较高,一般在10-2~ 10-4Pa,气体分子平均自由程比蒸发源到基体之 间的距离大。蒸发气相原子在向基体的飞行过程 中,蒸发气相原子之间或与残余气体分子间的碰 撞机会很少。它们将基本上保持离开蒸发源时所 具有的能量、能量分布和直线飞行轨迹。
在阴极溅射时,由于充入工作气体Ar气,真空 度较低,在100~10-2Pa左右,气体分子平均自由 程小于靶与基体之间的距离。溅射原子从靶面飞向 基体时,本身之间互相碰撞和Ar原子及其他残余气 体分子相互碰撞,不但使溅射粒子的初始能量减少, 而且还改变溅射粒子脱离靶面时所具有的方向。到 达基体表面的溅射粒子可来自基体正前方整个半球 面空间的所有方向。因此,溅射方法比蒸发方法较 容易制备厚度均匀的薄膜。
由于基体表面上吸附原子的扩散迁移碰撞结合,而不 是入射蒸发气相原子碰撞结合决定的。
薄膜的生长原理和技术

溅射过程的物理模型
入射离子 +
真空
靶材固体
溅射粒子 (离子或中性粒子)
渗透深度
注入离子
溅射产值
平均出射原子数 Y 入射离子数
依赖下面几个因素:
► 靶材材料的结构和 成分
► 入射离子束的参数 ► 实验环境的几何分
布
Yield
Sputtering Yield of Ar on Si
1
5 10 50 100 500
A Substrate
►周期结构多层膜
B A B A
Substrate
PVD的物理原理
衬底
扩散、吸附、凝 结成薄膜
物质输运 能量输运
能量
块状材料 (靶材)
PVD所需实验条件
►高真空 (HV) ►高纯材料 ►清洁和光滑的衬底表面 ►提供能量的能源
平均自由程、压强P和真空室尺寸L的关系
~ kT ~ L 2d 2 p
磁控溅射中的重要参数
► 溅射电流 ( 生长速率 ) ► 压强 ( 溅射粒子的最高能量 ) ► 压强与靶材-衬底之间的距离 (多孔性、质地、晶体
性) ► 反应气体混合比 ( 化学配比 ) ► 衬底温度 ( 晶体性、密度和均匀性 ) ► 衬底偏压 ( 薄膜结构和化学配比 )
⑤ MBE(分子束外延)
1. Introduction 2. Principle of MBE 3. In-situ analysis techniques 4. MBE systems 5. Applications 6. References
Ripening(成熟)
p 2
r
Clusters
大鱼吃小鱼!
Flux
Substrate
薄膜的生长过程PPT课件

2、在Si的(111)晶面上外延生长GaAs,由于第一层拥有五个价
电子的As原子不仅将使Si晶体表面的全部原子键得到饱和,而
且As原子自身也不再倾向于与其他原子发生键合。这有效地
降低了晶体的表面能,使得其后的沉积过程转变为三维的岛状
生长。
.
13
6.1薄膜生长过程概述
三、导致生长模式转变的三种物理机制
第六章 薄膜的生长过程
.
1
6.1薄膜生长过程概述
图6.1表示薄膜沉积中原子的运动. 状态及薄膜的生长过程
2
6.1薄膜生长过程概述
射向基板及薄膜表面的原子、分子与表面相碰撞,其中一部分 被反射,另一部分在表面上停留。
停留于表面的原子、分子,在自身所带能量及基板温度所对应 的能量作用下,发生表面扩散(surface diffusion)及表面迁移 (surface migration),一部分再蒸发,脱离表面,一部分落入 势能谷底,被表面吸附,即发生凝结过程。
也就是说,薄膜沉积伴随着从气相到固相的急冷过程,从结构 上看,薄膜中必然会保留大量的缺陷。
此外,薄膜的形态也不是块体的,其厚度与表面尺寸相比相差 甚远,可近似为二维结构。
.
4
6.1薄膜生长过程概述
一、薄膜的生长过程:新相的成核与薄膜的生长两个阶段
1、成核阶段
在薄膜形成的最初阶段,一些气态的原子或分子开始凝聚 到衬底上,从而开始了所谓的形核阶段。由于热涨落的作用, 原子到达衬底表面的最初阶段,在衬底上成了均匀细小、而且 可以运动的原子团(岛或核)。
6.2新相的自发成核理论
在薄膜沉积过程的最初阶段,都需要有新相的核心形成, 新相的成核过程可以被分为两种类型: 1. 自发成核:所谓自发成核指的是整个形核过程完全是在相 变自由能的推动下进行的; 2. 非自发成核:非自发形核指的是除了有相变自由能作推动 力之外,还有其他的因素起到了帮助新相核心生成的作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
γ = γ 0 + fαβ ε αβ
S
Reference state: unstrained surface!
A liquid membrane experiment
L
Variation of free energy:
W F
δG = 2γWδL − FδL
No friction
By principles of thermodynamics: In equilibrium:
t
Cluster coalescence
• Ostwald ripening: the desire to minimize surface energy drives atoms to diffuse from smaller islands to larger islands; larger islands grow or “ripen” at the expense of smaller ones. • Sintering: a neck forms when two clusters are in contact; atoms diffuse to the neck to reduce the total surface energy. • Cluster migration: clusters migrate on substrate surface and coalesce when they collide.
N
B C A
A: nucleus density increases B: nucleus density saturates at a stable value, depending on deposition rate and substrate temperature C: nucleus density decreases due to coalescence
∆G*
Homogeneous nucleation (θ = 180°)
θ = 0, ∆G* = 0
θ
Kinetics of nucleation
• Nucleation rate:
dN = N * A*ω dt
N*: equilibrium concentration of stable nuclei (per unit area) A*: critical area for atomic impinging ω: rate of atomic impinging (per unit area per unit time)
EM 397: Thin Film Mechanics
III. Growth Modes of Thin Films
Nanshu Lu
The University of Texas at Austin Fall 2013
Growth modes
• Layer-by-layer mode (Frank-van der Merwe or FM)
δG = 0
F = 2γW
Otherwise, free energy tend to decrease: δG < 0
F > 2γW F < 2γW
How about an elastic membrane?
δL > 0 δL < 0
Interface energy
• Same physical origin as surface energy • Consider a spherical cap cluster on a substrate:
– Initially FM growth – After a few monolayers, other energy contributions (e.g., strain energy) trigger the transition from layer to island growth.
γ s ≥ γ f + γ sf γ s < γ f + γ sf
Exposed bulk plane (unbalanced surface)
Surface atoms relaxed outward
Reconstruction of surface layers
Surface energy
• Atoms at a free surface are more energetic than atoms within the bulk • Create two surfaces by cutting a large block into two parts:
– free energy reduces by condensation (per atom):
∆GV = −kT ln p = −kT ln(1 + S ) pe
k = 1.38 × 10-23 J/K = 8.617 × 10-5 eV/K
Thermodynamics of nucleation
γf θ
2R
γsf
γs
Free energy:
G ( R, θ ) = γ f Af + (γ sf − γ s )πR 2
γf γs γsf
2πR 2 Af = 1 + cos θ πR 3 2 + cos θ 1 − cos θ Vf = 3 1 + cos θ sin θ
δG = 0 δVf = 0
∆G =
γf θ
2R
Vf
Ω
∆GV + γ f Af + (γ sf − γ s )πR 2
∆GV = −kT ln p pe
γsf
γs
πR 3 2 + cosθ 1 − cosθ Vf = 3 1 + cosθ sin θ
2πR 2 Af = 1 + cosθ
Critical nucleus
∆G ∆G* 0
– Homoepitaxy, e.g., Si on Si
• Island mode (Volmer-Weber or VW)
– Metal or semiconductor on oxide substrates
• Layer-plus-island (Stranski-Krastanov or SK)
γ f + γ sf > γ s > γ sf
γ s ≥ γ f + γ sf
θ
γ s < γ sf < γ s + γ f
γ sf ≥ γ s + γ f
Film growth modes
• In macroscopic terms, the three film growth modes can be understood based on the surface energies or simply the wetting angle. • FM mode: • VW mode: • SK mode:
– Heteroepitaxy, e.g., Ge on Si, GaN on saps of solid surfaces
• Substrate surface plays a very important role in the film growth process and influences the structures and properties of thin films. • Metal: increased electron density near a surface • Semiconductors: dangling bonds at a surface • Surface relaxation and reconstruction
∂∆G =0 ∂R
R* = 2γ f Ω − ∆GV sin θ
and
R R*
2 Ω 16πγ 3 (2 + cosθ )(1 − cosθ ) 2 f ∆G* = 3(∆GV ) 2 4
0 <θ <π
To reduce the free energy, nucleus shrinks and disappear if R < R*, and grows if R > R*. ∆G* is the barrier energy for nucleation. Equilibrium concentration of stable nuclei is
θ =0 θ >0
Vapor condensation
• At equilibrium pressure, atoms attach to and detach from the solid surface with equal probability, thus no net deposition. • When the vapor pressure is higher (supersaturated), more atoms attach to the solid surface
2 16πγ 3 Ω f
3(∆GV ) 2
• Heterogeneous nucleation:
– Substrate catalyze nucleation by lowering the energy barrier through the wetting angle – Strain energy due to lattice mismatch increases the barrier – Surface defects (crystalline steps, grain boundary traces, dislocations, impurities, etc.) could decrease the barrier.
