常见构造全等三角形的七种常用方法
构造全等三角形的四种技巧

构造全等三角形的四种技巧在几何学中,全等三角形是一个非常重要的概念。
全等三角形是指两个或两个以上的三角形,它们的形状和大小完全相同。
理解并能够构造全等三角形,对于解决各种几何问题有着至关重要的作用。
以下是构造全等三角形的四种技巧:利用公理:全等三角形的公理是:如果两个三角形的三边对应相等,那么这两个三角形全等。
这个公理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后根据这些边长画出两个三角形。
这两个三角形的形状和大小将会完全相同。
利用角平分线:角平分线定理指出,一个角的平分线将对应的边分为两段,这两段与角的两边形成的两个小三角形是全等的。
通过这个定理,你可以通过一个角的平分线,构造出一个全等三角形。
利用中垂线:中垂线定理指出,一条中垂线将一个线段分为两段,这两段与线段的两端形成的两个小三角形是全等的。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后通过中垂线将这些边分为两段。
这样,你就可以得到两个全等的三角形。
利用平行线:平行线定理指出,如果两条平行线被第三条直线所截,那么截得的对应线段成比例。
这个定理可以用来构造全等三角形。
确定你需要构造的全等三角形的所有边长,然后在两条平行线上画出对应的线段。
由于这些线段成比例,因此它们形成的两个小三角形是相似的。
如果这些相似三角形的对应边长度相等,那么它们就是全等的。
以上就是构造全等三角形的四种技巧。
理解和掌握这些技巧,对于解决各种几何问题有着重要的作用。
已知两个三角形全等,则它们对应边上的高也________;对应角平分线也________;对应边上的中线也________。
两个直角三角形全等,除了用定义外,还可以用以下________判定。
已知三角形ABC全等三角形DEF,且AB=18cm,BC=20cm,CA=15cm,则DE=________cm,DF=________cm,EF=________cm.做衣服需要依据身体部位的大小来选择布料,而教学则需要依据学生原有的知识基础来选择教学方法。
构造全等三角形的方法技巧

方法1 角形
利用“角平分线”构造全等三ห้องสมุดไป่ตู้
【方法归纳】 因角平分线本身已经具备 全等的三个条件中的两个(角相等和公共 边相等),故在处理角平分线问题时,常 作以下辅助线构造全等三角形: (1)在角的两边截取两条相等的线段; (2)过角平分线上一点作角两边的垂线.
思1.如图,AB∥CD,BE平分 ∠ABC,CE平分∠BCD,点E在AD 上,求证:BC=AB+CD. 考
2.如图,已知∠AOB=90°,OM是 ∠AOB的平分线,三角尺的直角顶点 P在射线OM上滑动,两直角边分别与 OA,OB交于点C,D,求证:PC= PD.
方法2 利用“截长补短法”构造全等 三角形
【方法归纳】 截长补短法的具体做法 :在某一条线段上截取一条线段与特定 线段相等,或将某条线段延长,使之与 特定线段相等,再利用三角形全等的有 关性质加以说明.这种方法适用于证明 线段的和、差、倍、分等类的题目.
3.如图,在△ABC中,AD平分 ∠BAC,∠C=2∠B,试判断AB, AC,CD三者之间的数量关系,并 说明理由.(想一想,你会几种方法)
方法3 利用“倍长中线法”构造全 等三角形
【方法归纳】 将中点处的线段延长 一倍,然后利用SAS证三角形全等.
6.已知:如图,AD,AE分别是 △ABC和△ABD的中线,且BA= BD.求证:AE=AC.
构造全等三角形的六种常用方法课件

构造方法简介
01
02
03
04
尺规作图法
利用尺规作图工具,通过已知 条件构造全等三角形。
翻折法
将已知三角形沿某条直线翻折, 得到与原三角形全等的三角形。
平移法
将已知三角形沿某方向平移一 定距离,得到与原三角形全等
的三角形。
旋转法
将已知三角形绕某点旋转一定 角度,得到与原三角形全等的
三角形。
02 方法一:SSS全 等法
感谢观看
拓展延伸:其他构造方法及应用场景
构造中位线
利用三角形中位线性质构 造全等三角形,常用于证 明线段相等或倍长中线等 问题。
构造角平分线
利用角平分线性质构造全 等三角形,常用于证明角 相等或线段成比例等问题。
构造垂直平分线
利用垂直平分线性质构造 全等三角形,常用于证明 线段相等或点共圆等问题。
THANKS
判定条件
两个三角形中,两个角及这两个角的夹边分别相等,则这两个三角形全等。
构造步骤这两个角的夹边相等,最后根据ASA判定条件证明两个三角形全等。
示例
在△ABC和△ADE中,∠BAC=∠DAE,∠B=∠D,AB=AD。根据ASA全等法,可以判定△ABC≌△ADE。
应用场景分析
1 2 3
解决角度和边长问题 当题目中给出两个角和它们的夹边相等时,可以 利用ASA全等法证明两个三角形全等,从而解决 与角度和边长相关的问题。
构造全等三角形 在几何证明题中,有时需要构造全等三角形以证 明某些线段或角度相等。ASA全等法是构造全等 三角形的常用方法之一。
辅助线策略 当遇到复杂的几何问题时,可以通过作辅助线构 造全等三角形,将问题转化为已知的全等三角形 问题,从而简化解题过程。
2020最新名校课堂小专题4:构造全等三角形的常用方法

小专题4:构造全等三角形的常用方法方法1 利用“角平分线”构造全等三角形模型构建已知点P是MON⊥于⊥于点A,可以过点P作PB ON ∠平分线上一点,若PA OM点B,则PB PA=.1.感知:如图,AD平分18090,,,易知:.∠∠+∠=︒∠=︒=BAC B C B DB DC探究:如图,AD平分18090∠∠+∠=︒∠<︒,,,求证:BAC ABD ACD ABD=.DB DC模型构建若AOP BOP=,∠=∠,且点A是射线OM上任意一点,可以在ON上截取OB OA 连接PB,构造OPB OPA≌.∆∆2.如图,//∠,点E在AD上,求证:AB CD,BE平分ABC∠,CE平分BCD=+.BC AB CD方法2 利用截长补短法构造全等三角形方法指导截长补短法的具体做法:在某一条线段上截取一条线段与特定线段相等,或将某条线段延长,使之与特定线段相等,再利用三角形全等的有关性质加以说明,这种方法适用于证明线段的和差、倍、分等题目.3.问题背景:如图,在四边形ABCD中,12090AB AD BAD B ADC=∠=︒∠=∠=︒,,.点E,F分别是BC,CD上的点,且60EAF︒∠=.探究图中线段BE,EF,FD之间的数量关系.(1)小王同学探究此问题的方法是:延长FD到点G,使DG BE=,连接AG.先证明ABE ADG∆∆≌,再证明AEF AGF∆∆≌,可得出结论,他的结论应是______; (2)如图,若在四边形ABCD中,180AB AD B D=∠+∠=︒,.E,F分别是BC,CD上的点,且12EAF BAD∠=∠,上述结论是否仍然成立?并说明理由.方法3 利用“倍长中线法”构造全等三角形方法指导将中线延长一倍,然后利用“SAS”判定三角形全等.4.如图,AB AE AB AE AD AC AD AC=⊥=⊥,,,,点M为BC的中点,求证:2DE AM=.方法4 利用“三垂直”构造全等三角形模型构建如图,若AB AC AB AC,,则可过斜边的两端点B,C向过A点的直线作垂线=⊥构造ABD CAE≌.在平面直角坐标系中,过顶点A的直线常为x轴或y轴.∆∆5.已知在△ABC中,90,,将△ABC放在平面直角坐标系中,如BAC AB AC∠=︒=图所示.(1)如图,若A(1,0),B(0,3),求C点坐标;(2)如图,若A(1,3),B(10-,),求C点坐标;(3)如图3,若B(40,),求A点坐标.-,),C(01-参考答案1.证明:过点D 作DE AB ⊥于点E ,DF AC ⊥交AC 的延长线于点F . AD 平分90BAC DE AB DF AC DE DF F DEB ∠⊥⊥∴=∠=∠=︒,,,,. 180180EBD ACD ACD FCD EBD FCD ∠+∠=︒∠+∠=︒∴∠=∠,,.在△DFC 和△DEB 中,,,,F DEB FCD EBD DF DE ∠=∠⎧⎪∠=∠⎨⎪=⎩DFC DEB ∴∆∆≌(AAS ).DC DB ∴=.2.证明:在BC 上截取BF AB =,连接EF . BE 平分ABC ∠,CE BCD ∠平分,ABE FBE FCE DCE ∴∠=∠∠=∠,.在△ABE 和△FBE 中,,,,AB FB ABE FBE BE BE =⎧⎪∠=∠⎨⎪=⎩ABE FBE ∴∆∆≌(SAS ),A BFE ∴∠=∠.//180.180AB CD A D BFE D ∴∠+∠=︒∴∠+∠=︒,. 180BFE CFE CFE D ∠+∠=︒∴∠=∠,.在△FCE 和△DCE 中,,,,CFE D FCE DCE CE CE ∠=∠⎧⎪∠=∠⎨⎪=⎩FCE DCE ∴∆∆≌(AAS )..CF CD BC BF CF AB CD ∴=∴=+=+.3.解:(1)EF BE FD =+(2)EF BE FD =+仍然成立.理由:延长FD 到G ,使DG BE =,连接AG ,180180B ADC ADC ADG B ADG ∠+∠=︒∠+∠=︒∴∠=∠,,.在△ABE 和△ADG 中,,,,BE DG B ADG AB AD =⎧⎪∠=∠⎨⎪=⎩ABE ADG ∴∆∆≌(SAS ).AE AG BAE DAG ∴=∠=∠,.12EAF BAD ∠=∠, GAF DAG DAF BAE DAF BAD EAF EAF ∴∠=∠+∠=∠+∠=∠-∠=∠.在△AEF 和△AGF 中,,,,AE AG EAF GAF AF AF =⎧⎪∠=∠⎨⎪=⎩AEF AGF ∴∆∆≌(SAS ).EF FG ∴=.FG DG DF BE DF EF BE DF =+=+∴=+,.4.证明:延长AM 至N ,使MN AM =,连接BN .点M 为BC 的中点,BM CM ∴=.在△AMC 和△NMB 中,,,,AM NM CMA BMN CM BM =⎧⎪∠=∠⎨⎪=⎩AMC NMB ∴∆∆≌(SAS ).AC BN AD C NBM ∴==∠=∠,.180ABN ABC NBM ABC C BAC EAD ∴∠=∠+∠=∠+∠=︒-∠=∠.在△ABN 和△EAD 中,,,,AB EA ABN EAD BN AD =⎧⎪∠=∠⎨⎪=⎩ABN EAD ∴∆∆≌(SAS ).2DE NA AM ∴==.5.解:(1)过点C 作CD x ⊥轴,垂足为D .则90CAD ACD ∠+∠=︒. 9090.BAC BAO CAD BAO ACD ∠=︒∴∠+∠=︒∴∠=∠,.在△ABO 和△CAD 中,,,,AOB CDA BAO ACD AB CA ∠=∠⎧⎪∠=∠⎨⎪=⎩ABO CAD ∴∆∆≌(AAS ).BO AD OA CD ∴==,.A (1,0),B (0,3)1 3.31OA OB AD CD ∴====,,,. 4.OD OA AD ∴=+=∴C (4,1).(2)过点A 作AD x ⊥轴,垂足为D ,过点C 作CE AD ⊥,垂足为E .同(1)可证ACE BAD AE BD CE AD ∆∆∴==≌,,.A (1,3),B (10-,),2 3.3 1.BD AD CE DE AD AE ∴==∴==-=∴,,C (4,1).(3)过点A AD x AE y ⊥⊥作轴,轴,垂足分别为D ,E .同(1)可证BAD CAE ∆∆≌,CE BD AE AD OE ∴===,. B (40-,),C (01-,),4 1.OB OC ∴==, 3.AE OB BD OB CE OB OC OE AE ∴=-=-=-+=-()333(,)222AE A ∴=⋅∴-。
构造全等三角形的常用方法
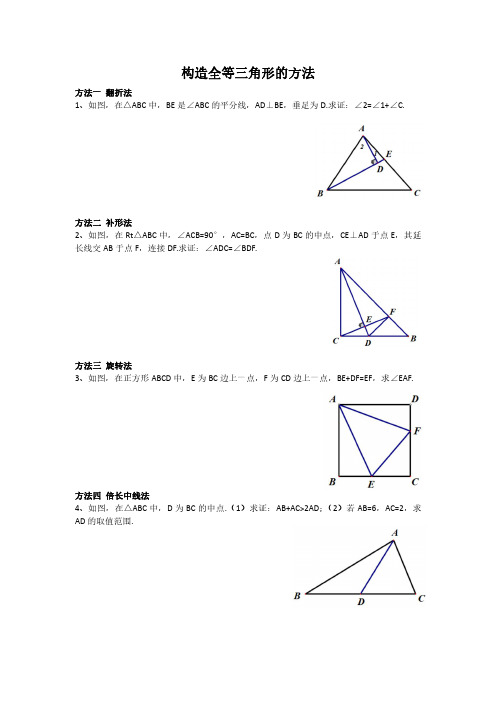
构造全等三角形的方法
方法一翻折法
1、如图,在△ABC中,BE是∠ABC的平分线,AD⊥BE,垂足为D.求证:∠2=∠1+∠C.
方法二补形法
2、如图,在Rt△ABC中,∠ACB=90°,AC=BC,点D为BC的中点,CE⊥AD于点E,其延长线交AB于点F,连接DF.求证:∠ADC=∠BDF.
方法三旋转法
3、如图,在正方形ABCD中,E为BC边上一点,F为CD边上一点,BE+DF=EF,求∠EAF.
方法四倍长中线法
4、如图,在△ABC中,D为BC的中点.(1)求证:AB+AC>2AD;(2)若AB=6,AC=2,求AD的取值范围.
方法五截长补短法
5、如图,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°.E、F分别是BC、CD 上的点,且∠EAF=60°.探究图中线段BE、EF、FD之间的数量关系并证明.
方法六作垂线法
6、如图,∠AOB=90°,OM平分∠AOB,直角三角板的顶点P在射线OM上移动,两直角边分别与OA,OB相交于点C、D,问PC与PD相等吗?试说明理由.
方法七作平行线法
7、如图,△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC交BC于点P,BQ平分∠ABC 交AC于点Q.求证:AB+BP=BQ+AQ.。
初中数学三角形全等常用几何模型及构造方法大全初二

初二数学三角形全等常用几何模型及构造方法大全掌握它轻松搞定全等题!全等是初中数学中非常重要的内容,一般会在压轴题中进行考察,而掌握几何模型能够为考试节省不少时间,这次整理了常用的各大模型,一定要认真掌握~全等变换类型:(一)平移全等:平行等线段(平行四边形)(二)对称全等模型:角平分线或垂直或半角1:角平分线模型;2:对称半角模型;(三)旋转全等模型:相邻等线段绕公共顶点旋转1.旋转半角模型2.自旋转模型3.共旋转模型4.中点旋转如图,在△ABC的边上取两点D、E,且BD=CE,求证:AB+AC>AD+AE分析:将△ACE平移使EC与BD重合。
B\D,上方交点,左右两个三角形,两边和大于第三边!1:角平分线模型:说明:以角平分线为轴在角两边进行截长补短或者作边的垂线,形成对称全等。
两边进行边或者角的等量代换,产生联系。
垂直也可以做为轴进行对称全等。
2:对称半角模型说明:上图依次是45°、30°、 45+ °、对称(翻折)15°+30°直角三角形对称(翻折) 30+60+90直角三角形对称(翻折)翻折成正方形或者等腰直角三角形、等边三角形、对称全等。
1.半角:有一个角含1/2角及相邻线段2.自旋转:有一对相邻等线段,需要构造旋转全等3.共旋转:有两对相邻等线段,直接寻找旋转全等(共顶点)4.中点旋转:倍长中点相关线段转换成旋转全等问题(专题七)1、旋转半角模型说明:旋转半角的特征是相邻等线段所成角含一个二分之一角,通过旋转将另外两个和为二分之一的角拼接在一起,成对称全等。
2、自旋转模型构造方法:遇60度旋60度,造等边三角形遇90度旋90度,造等腰直角遇等腰旋顶点,造旋转全等遇中点旋180度,造中心对称3、共旋转模型说明:旋转中所成的全等三角形,第三边所成的角是一个经常考察的内容。
通过“8”字模型可以证明。
(接上------共旋转模型)模型变形说明:模型变形主要是两个正多边形或者等腰三角形的夹角的变化,另外是等腰直角三角形与正方形混用。
构造全等三角形的方法专题
知识体系利用三角形全等是证明线段或角相等的重要方法之一,但有时不能直接应用,就需要根据条件,通过作辅助线的方法构造全等三角形。
构造全等三角形的方法主要有:中线倍长,截长补短,翻折,作平行线或垂线。
(1)遇到与中点有关的条件时,通常将过中点的线段延长一倍,构造 字形全等三角形。
(2)证一条线段等于另外两条线段和或差时,通常在较长的线段上截取一条线段等于较短的线段中的某一条,(此谓之“截长”),或将两条较短的线段转化到一条线段上,(此谓之“补短”)注意:不管是截长还是补短,都要证明截取或补上的线段所在的三角形与另一个对应三角形全等。
(3)遇角平分线时,通常用翻折构造全等或向角两边作垂线构造全等。
例题选讲例1如图,在△ABC 中,AD 是∠BAC 的平分线,M 是BC 的中点,过M 作MF ∥AD 交BA 的延长线于F ,交AC 于P ,求证:CP =BF =21(AB +AC )例2如图,△ABC 中,D 为BC 的中点,M 为AB 上一动点,N 为AC 上一动点,且∠MDN =90°.(1)求证:BM +CN >MN ;FP MD C B A A M N C B D(2)若M在AB的延长线上,N在CA的延长线上,其它条件不变,(1)中的结论是否仍然成立,若成立,请证明,若不成立,说明理由;(3)若点M在BA的延长线上,点N在AC的延长线上,其它条件不变,(1)中的结论是否仍然成立,若成立,请证明,若不成立,说明理由。
例3如图,在四边形ABCD中,AD=DC,BD平分∠ABC,求证:∠A+∠C=180°变形1,如图,在四边形ABCD中,∠A+∠C=180°,BD平分∠ABC,求证:AD=DC变形2,如图,在四边形ABCD中,DE⊥BC于E,BD平分∠ABC,若BE=12(AB+AC),求证:∠A+∠C=180°ACBDMBACNADC BADCBADCB E变形3,如图,在四边形ABCD 中,DE ⊥BC 于E ,BD 平分∠ABC ,若∠A +∠C =180°,求证:BE =12(AB +BC )例4已知AM ∥BN ,AC 平分∠MAB ,BC 平分∠NBA① 过C 作直线DE ,分别交AM 、BN 于点D 、E ,求证:AB =AD +BE ;② 将直线绕C 转动,使DE 与AM 交于点D ,与NB 的延长线交于点E ,则AB 、AD 、BE 三条线段是否存在确定的数量关系?例5已知如图,在正方形ABCD 中AB =AD ,∠B =∠D =90°.(1)如果BE +DF =EF ,求证:①∠EAF =45°;②FA 平分∠DFE .(2)如果∠EAF =45°,求证: BE +DF =EF .A B C DE M N A B C D E M N A B CD E F A D CBEA CB F D(3)如果点F 在DC 的延长线上,点E 在CB 的延长线上,满足(1)的条件,则(1)中结论是否仍然成立? 巩固练习1.已知: 如图, AD 为△ABC 的中线, 且∠1 = ∠2, ∠3 = ∠4. 求证: BE +CF >EF说明:有角平分线时常在角两边截相等的线段, 构造全等三角形.2.已知,如图,△ABC (AB ≠AC )中,D 、E 在BC 上,且DE =EC ,过D 作DF ∥BA 交AE 于点F ,DF =AC ,求证:AE 平分∠BAC 。
初中数学——构造全等三角形的五种常用方法
所以∠1=∠2. ∠1=∠2,
在△ACD 和△CBG 中,AC=CB, ∠ACD=∠CBG=90°,
所以△ACD≌△CBG(ASA). 所以∠ADC=∠G,CD=BG. 因为点 D 为 BC 的中点,所以 CD=BD.所以 BD=BG. 因为∠DBG=90°,∠DBF=45°,
所以∠GBF=∠DBG-∠DBF=90°-45°=45°.
解:如图,过点B作BG⊥BC交CF的延长线于点G. 因为∠ACB=90°,所以∠2+∠ACF=90°. 因为CE⊥AD, 所以∠AEC=90°. 所以∠1+∠ACF=180°-∠AEC=180°-90°=90°. 因为CE⊥AD,所以∠AEC=90°. 所以∠1+∠ACF=180°-∠AEC=180°-90°=90°.
在△AEH 和△AEF 中,AE=AE, EH=EF,
所以△AEH≌△AEF(SSS).
所以∠EAH=∠EAF.
所以∠EAF=12∠HAF=45°.
返回
方 法 4 倍长中线法
4.如图,在△ABC中,D为BC的中点.若AB=5, AC=3,求AD长度的取值范围. 解:如图,延长AD至点E,使DE= AD,连接BE. 因为D为BC的中点,所以CD=BD.
第四章 三角形
构造全等三角形的五种常用方法
方 法 1 翻折法
1.如图,在△ABC中,BE是∠ABC的平分线, AD⊥BE,垂足为D.试说明:∠2=∠1+∠C.
解:如图,延长AD交BC于点F(相当于将AB边向下翻 折,与BC边重合,A点落在F点处,折痕为BE). 因为BE平分∠ABC, 所以∠ABE=∠CBE. 因为BD⊥AD, 所以∠ADB=∠FDB=90°.
所以∠D=∠ABH=90°. AB=AD,
在△ABH 和△ADF 中,∠ABH=∠D=90°, BH=DF,
构造三角形全等的几种方法
专题构造三角形全等的几种方法
类型一:利用“倍长中线法”构造全等三角形
1、已知在△A B C中,A B=4cm,A C=6cm.求第三边上中线A D的取值范围.
2、如图.AB=AE,AB⊥AE,AD=AC.AD⊥AC,点M为BC的中点,求证:DE=2AM.
类型二、利用“截长补短法”构造全等三角形3、如图,在△ABC中,AD平分∠BAC,∠C=2∠B,试判断AB,AC,CD三者之间的数量关系,并说明理由.4、已知:如图,在△ABC中.∠BCA=90°,AC=BC,AE平分∠BAC,BE⊥AE.求证:BE=AD.
5、如图,点E、F分别在正方形ABCD的边BC、CD上,∠EAF=45°,连接EF,求证:EF=BE+DF.
类型三:利用角平分构造全等三角形
6、如图,AD是△ABC中∠BAC的平分线,P是AD上的任意一点,且AB>AC,求证:AB﹣AC>PB﹣PC.
7、如图,△AOB中,OA=OB,∠AOB=90゜,BD平分∠ABO交OA于D,AE⊥BD于E.
求证:BD=2AE.
类型四:通过作平行线构造全等三角形
8、如图,△ABC中,AB=AC,在AB上取一点E,在AC的延长线上取一点F,使CF=BE,连接EF,交BC于点D.求证:DE=DF.
9、△ABC中,∠BAC=60°,∠C=40°,AP平分∠BAC 交BC于P,BQ平分∠ABC交AC于Q,求证:
AB+BP=BQ+AQ.。
小专题(三) 构造全等三角形的常用方法
AB=FB, ∠ABE=∠FBE, BE=BE,
∴△ABE≌△FBE(SAS). ∴∠A=∠BFE.
∵AB∥CD, ∴∠A+∠D=180°. ∴∠BFE+∠D=180°. ∵∠BFE+∠CFE=180°, ∴∠CFE=∠D. 在△FCE和△DCE中,
方法2 利用“截长补短法”构造全等三角形
截长补短法的具体做法:在某一条线段上截取一条线 段与特定线段相等,或将某条线段延长,使之与特定线段 相等,再利用三角形全等的有关性质加以说明.这种方法 适用于证明线段的和、差、倍、分等题目.
2.如图,AB∥CD,BE平分∠ABC,CE平分∠BCD,点 E在AD上,求证:BC=AB+CD.
∠CFE=∠D, ∠FCE=∠DCE, CE=CE,
∴△FCE≌△DCE(AAS). ∴CF=CD. ∴BC=BF+CF=AB+CD.
3.(德州中考)问题背景: 如图1,在四边形ABCD中,AB=AD,∠BAD=120°, ∠B=∠ADC=90°.点E,F分别是BC,CD上的点,且 ∠EAF=60°.探究图中线段BE,EF,FD之间的数量关系. (1)小王同学探究此问题的方法是:延长FD到点G,使 DG=BE,连接AG.先证明△ABE≌△ADG,再证明 △AEF≌△AGF,可得出结论,他的结论应是 EF=BE+DF;
(2) 如图 2,若在四边形 ABCD 中,AB=AD, ∠B+∠D=180°.E,F 分别是 BC,CD 上的点,
且∠EAF=12∠BAD,上述结论是否仍然成立?并说明理由. 解:EF=BE+DF仍然成立. 理由:延长FD到G,使DG=BE,连接AG, ∵∠B+∠ADC=180°,∠ADC+∠ADG=180°, ∴∠B=∠ADG. 在△ABE和△ADG中,
