平面图(new)_46002149
2100平米4层框架结构娱乐会所平立剖面设计CAD图纸(含地下室)

施工平面图参考图例(最新版)

临时排水沟
2
临时水池
18
化粪池
3
贮 水 池
19
拟建水源
4
永 久 井
20
电源
5
临 时 井
21
变压器
6
加 压 井
22
投光灯
7
原有的上水管线
23
电杆
8
临时给水管线
24
现在高压6kv线路
9
给水阀门(水嘴)
25
施工期间利用的永久高压6kv线路
10
支管接管位置
26
临时高压3—5kv线路
11
消火栓
27
现有低压线路
12
原有上下水井
28
施工期间利用的永久低压线路
13
拟建上下水井
29
临时低压线路
14
临时上下水井
30
电话线
15
原有的排水管线
31
现有暖气管道
16
临时排水管线
32
临时暖气管道
六、施工机械
1
塔式起重机
8
挖土机:正 铲
反 铲
抓 铲
拉 铲
2
井 架
9
推土机
3
门 架
10
铲运机
4
卷扬机
11
混凝土搅拌机
5
履带式起重机
12
灰浆搅拌机
6
汽车式起重机
13
打桩机
7
外用电梯
14
水 泵
七、其 他
1
脚手架
3
草坪
2
壁板插放架
4
避雷针
6
围墙及大门
2
总用地198亩住宅总套数964小区规划总平面图

房建施工平面图---副本
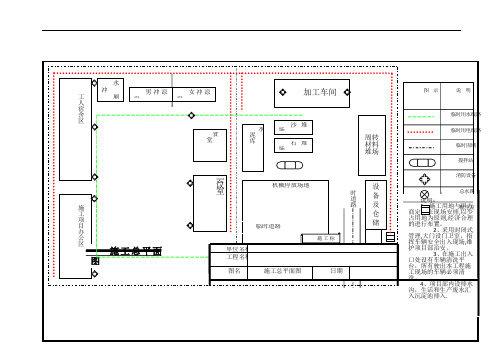
2临时道路
临
时
道
路
施工标志栏
门
卫
室
设
备
及
仓
储
周
转材
料堆
场
施工
项
目
办
公
区
工人
宿
舍
区
厕所
男冲
凉房
女冲
凉房
会
议
室
食
堂
机械停放场地
加工车间
水
泥
库
材料堆放场
搅
拌站
图示说
明
临时用
水线路
临时用电
线路
临时围
墙
消防设
备
说明:
1、施工用地与甲方商定后在现
场安排,以少占用地方为原则,经济
合理进行布置。
2、采用封闭式管理,大门设门
卫室,指挥车辆安全出入现场及治
安。
3、在施工出入口设车辆清洗平台,
所有驶出车辆必须清洗。
4、在附近引用生活给水及电
钱,均埋地敷设。
项目部内设排水沟,生活和生产废水
汇入沉淀池排入。
拟建工程。
完整版本总平面图图例.doc

总平面图图例序名称图例号1新建建筑物2原有建筑物计划扩建的预留3地或建筑物4拆除的建筑物建筑物下面的通5道散状材料露天堆6场其他材料露天堆7场或露天作业场GB/T5013 ~2001备注1.需要时,可用▲表示出入口,可在图形内右上角用点数或数字表示层数。
2.建筑物外形(一般以±0.00高度处的外墙定位轴线或外墙线为准)用粗实线表示。
需要时,地面以上建筑用中粗实线表示,地面以下建筑用细虚线表示。
用细实线表示用中粗虚线表示用细实线表示需要时可注明材料名称需要时可注明材料名称8铺砌场地9敞棚或敞廊序名称号10高架式料仓11漏斗式贮仓12冷却塔(池)13水塔、贮罐14水池、坑槽、孔洞15明溜矿槽(井)16斜井或平洞总平面图图例GB/T5013 ~2001 图例备注左、右图为底卸式中图为侧卸式应注明冷却塔或冷却池左图为水塔或立式贮罐右图为卧式贮罐也可以不涂黑17烟囱18挡土墙实线为烟囱下部直径,虚线为基础。
必要时可注写烟囱高度和下、下口直径。
被档土在“突出”的一侧总平面图图例序名称图例号19档土墙上设围墙20围墙及大门21台阶22露天桥式起重机GB/T5013 ~2001备注被档土在“突出”的一侧上图为实体性质的围墙。
下图为通透性质的围墙,如铁丝网、篱笆等。
若仅表示围墙时不画大门。
箭头指向表示向下“ + ”为柱子位置23露天电动葫芦“ +”为支架位置24门式起重机25架空索道上图表示有外伸臂下图表示无外伸臂“ I ”为支架位置总平面图图例序名称图例号26斜坡卷扬机道斜坡栈桥27(皮带廊等)28坐标方格网交叉点29标高填方区、挖方区、30未整平区及零点线31填挖边坡32护坡GB/T5013 ~2001备注细实线表示支架中心线位置上图表示测量坐标下图表示建筑坐标“ 78.35 ”为原地面标高“ 77.85 ”为设计标高“ -0.50 ”为施工高度“ - ”表示挖方,“ + ”表示填方“ + ”表示填方区“ - ”表示挖方区中间为未整平区点划线为零点线1.边坡较长时,可在一端或两端局部表示。
某地区住宅楼建筑平面图纸(全套)

(完整word版)通用施工现场平面布置图

施工总平面图通用版一、临时设置布局说明二、安排计划说明结合施工现场实际情况,对施工现场平面及临时设施进行合理布局,实施封闭式管理。
所有临时用房都在科室门牌做出标志,墙面及天棚均采用空心板屋面。
卫生间、淋浴间及厨房等地面、墙裙铺设面砖,所有生活用房要求文明整洁。
在仓库、食堂等易燃易爆处配置足够的消防设施,预防各种安全隐患的放生。
1、临时施工道路施工主通道由城市道路到施工现场入口进出,场外交通道路利用现有城市道路,场内施工铺设临时道路。
2、临时供水布置临时用水包括施工用水、生活用水、消防用水。
其中施工用水包括砼及砂浆搅拌、养护、浇砖、模板湿润等。
配水管网的布置方法根据本公司以往类似工程经验,主杆线采用中48镀锌管,支管采用中25镀锌管。
现场用水采用环向封闭布置,优点是能保证供水的可靠性,当管网某一处发生故障时,水仍可以正常使用。
3、临时供电布置(1)施工用电的估算:施工现场用电分动力与照明两类,照明用电按动力用电的10%计算。
经用电量计算,在高峰施工期,考虑砼拦和、砼泵送、钢筋、木工加工、铺装面板切割加工、水泵排水、生活照明用电等共计总用量为250KW。
(2)配电线路布置根据总用电量,配电电压380/220V引自建设方提供的电源,采用三相五线制架空配置,分支线用25平方塑料铜芯线接至各用电设备。
线路应尽量架设在道路内侧,保持线路水平,电线杆采用木杆,间距30米,分支线及引入线均应由电杆处接出。
施工用电的配电箱要求设置于便于操作的地方,一般离地面高度不小于1.2米,并且安装漏电保护器,配电箱必须使用劳动部门检验合格的产品。
4、材料堆场根据本工程的实际情况,钢筋堆在现场仓库内并设加工棚。
各种材料堆放,必须整齐、规范,铺装面板加工场及堆场计划分二处设置,具体见平面布置图。
5、施工场地排水为确保施工期间场内排水畅通,施工前必须对本工程排水系统进行综合规划:(1)在施工场地周边开挖纵向排水边沟排水边沟底宽0.5米,深0.6米,沟内采用10cm细石砼铺底,240砖墙护坡,并且用水泥砂浆粉刷,沟底纵坡不小于0.3%。
各类小区、学校、别墅、规划总平面图
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
例如右图. 注: 平面图 画法不唯一.
v1 v2 v4 v3 v5 v2 v4
v1 v3 v5
下面是两个 v1 重要的非平面图 v:2 K5和K3,3 v4 1 2 3 v5 f e d b c d v2 v4 a v3 v5 f e
对偶图的性质
1. G*是连通的. 2. G*是平面图. 3. 若G是平面连通图, 则(G*)*=G. 4. m(G*)=m(G), n(G*)=r(G), d(v*)=d(f). 5. 设C是平面图G的一个圈, S*是G*中与C的各边ei对应的 G*的边集合 , 则S*是G*的一个割集. 证明: ∵ C把G的域分成两部分, ∴ E(G*)-S*把G*的点分 成不连通的两部分.
Proposition The dual G* of a plane graph G is itself a planar graph. In fact, there is a natural embedding of G* in the plane. We place each vertex f* in the corresponding face f of G, and then draw each edge e* in such a way that it crosses the corresponding edge e of G exactly once (and crosses no other edge of G). It is intuitively clear that we can always draw the dual as a plane graph in this way, but we do not prove this fact
2.对偶图(偶图)的定义:
给定平面图G=<V,E>, 可以定义另一个图 G*=<V*,E*>,如下: 1. 对于G的每个面f, 都有G*的顶点f*与之对应. 2. 对于G的每条边e, 都有G*的边e*与之对应. 3. G*中的点f*与g*被边e*相连 G中的面f和g被e分隔. 图G*称为G的对偶图.
Euler公式的推广形式
定理:对任意p(p≥1)个连通分支的平面图G,
有 n-m+r=p+1。 推论:对任意平面图G,有 n-m+r≥2。
Corollary 1. Let G be a simple planar graph on at least three vertices. Then m ≤ 3n − 6. Furthermore, m = 3n − 6 if and only if every planar embedding of G is a triangulation. Proof: It clearly suffices to prove the corollary for connected graphs. Let G be a simple connected planar graph with n ≥ 3 Consider any planar embedding G of G. Because G is simple and connected, on at least three vertices, d(f) ≥ 3 for all f ∈ F( G). Therefore, by Euler’s Formula (1)
Proposition
Let G be a planar graph, and let f be a face in some planar embedding of G. Then G admits a planar embedding whose outer face has the same boundary as f.
Proposition
The dual of any plane graph is
connected. Proof Let G be a plane graph and G* a plane dual of G. Consider any two vertices of G*. There is a curve in the plane connecting them which avoids all vertices of G. The sequence of faces and edges of G traversed by this curve corresponds in G* to a walk connecting the two vertices.
n
(i 2)( f
i3
i1
fi 2 ) 0
证明:G的边被分成三类:在C上、C的内部(称内弦)、 C的外部(称外弦) 以m1表示内弦的数目,则C内部的面数为m1 +1
n
故
i3
f i 1 m1 1
因为每条内弦是C内部两个面的边界,而C上的边恰 好是C内部的一个面的边界
n if 2 m n 2 f 1 所以 i1 1 i1 n i3 i3
2=n-m+r≤6-9+4=1 矛盾。
Corollary All planar embeddings of a connected planar graph have the same number of faces.
Proof
极大平面图(maximal planar)
定义: 设G为一个n≥3的简单平面图, 若在G中任意不 相邻的两个顶点之间再加一条边所得图为非平面图, 则称G为极大平面图.
定理1. (1)K5是非平面图.
证明: (1)(反证法) intC1 若有可能, 设G是对应K5的一个 平面图, 用v1, v2, v3, v4, v5表示G的顶点. intC2 intC3 ∵ G是完全图, ∴ vi vjE(G), ij. 因此圈C= v1v2 v3 v1是一条平面Jordon曲 线, 而点v4必然在intC内或extC内. 假设 v4intC, 则v1 v4, v2 v4, v3 v4把intC分成三个区域:int C1, int C2, int C3. v5必然在四个区域extC, int C1, int C2, int C3之一中.若 v5extC, ∵ v4intC, 从Jordan曲线定理知, 边v4v5必然 在某点和C相交. 矛盾. 若v5intCi, 如v5intC1, ∵v3extC1, ∴ 边v5v3必然在某点和C1相交. 矛盾. (2)的证明类似。
defined by π(s) = p if and only if the points z, s, and p are collinear, is called a stereographic projection from z
Theorem
A graph G is embeddable on the plane if and only if it is embeddable on the sphere.
(2)K3,3是非平面图.
二、对偶图(dual)
1. 平面图的面、边界及面的次数 设G是个平面图, 图中边围 成的区域,其内部不含有结点, 也不含有边,称这样区域为G 的一个面(域)(face). 面的边界(boundary):围成一个面f的所有 边构成的回路,称之为这个f面的边界. 此回路中的边 数,称之为面f的度数,记作d(f). 注1:在计算面的度时,割边被计算两次。 注2:每个平面恰有一个无界的面----外部分(outer face). F(G): 平面G中面的集合 . r(G)=|F(G)|----面的个数.
Consider a sphere S resting on a plane P, and denote by z the point that is diametrically opposite the point of contact of S and P. The mapping
π : S \{z} → P,
v3*
v5
v1* F1 F2 v * 2
F3
Note:
isomorphic plane graphs may well have nonisomorphic duals.
Theorem If G is a plane graph, then
定理:设G是n阶平面图,G含有H圈C,以fi1, fi2分别表示在C 的内部和外部的、度为i的面数,则
t (n 2) m t2
推论:K5是非平面图.
推论2. 若G是简单连通平面图, 则≤5.
证:
当n=1, 2时, 结论显然成立. d ( v ) 2m 由推论1,有 若n≥3,
vV
n d( v ) 2m 6n 12.
∴
vV
≤5.
推论3. K3,3是非平面图.
equivalently, m ≤ 3n − 6 (2) Equality holds in (2) if and only if it holds in (1), that is, if and only if d(f) = 3 for each f ∈ F( G).
推论1’:设平面图G是简单图,且每个面的边界数至少 是t,则有
Proof:
Jordon曲线: 一条连续的, 自身不相交的, 起点 和终点相重合的曲线. 设J是平面上的一条Jordon曲线, 平面的剩下部 分被分成两个不相交的开集, 称为J的内部和外 部, 分别记为intJ和extJ, 并且用IntJ和ExtJ表 示它们的闭包. 显然IntJExtJ=J. Jordon曲线定理(The Jordan Curve Theorem): 连接intJ的点和extJ的点的任何连线必在某点 和J相交.
