从随机积分到数学金融
如何利用数学解决经济与金融问题

如何利用数学解决经济与金融问题在现代社会,数学不仅是一门学科,更是一种思维方式和工具。
数学的应用范围十分广泛,除了在科学领域,它也在经济与金融领域发挥了重要作用。
本文将探讨如何利用数学解决经济与金融问题。
一、数学模型在经济与金融中的应用数学模型是指用数学语言和符号表示现实世界中的某种实际问题。
在经济与金融中,数学模型可以解决许多复杂的问题,例如市场供求关系、价格弹性、投资决策等等。
通过建立数学模型,我们可以对经济活动进行量化分析和预测,提供决策依据。
二、统计学在金融市场的应用统计学是数学的一个分支,广泛应用于金融市场的分析和决策。
统计学通过对历史数据的分析和处理,可以预测未来市场的趋势和走势。
例如,通过对过去几年的股票价格数据进行统计分析,可以得出某只股票未来的涨跌概率。
三、微积分在金融中的应用微积分是数学的一个重要分支,也是解决经济与金融问题的重要工具。
微积分可以帮助我们求解极值问题、优化问题等。
例如,在投资决策中,我们可以利用微积分来确定最优的投资组合,以最大化收益或最小化风险。
四、线性代数在金融分析中的应用线性代数是数学的一个基础分支,也是金融分析中不可或缺的工具。
线性代数可以用来解决多元线性回归、矩阵运算等问题。
例如,在建立投资组合模型时,我们可以利用线性代数的方法对各种资产的权重进行计算。
五、概率论与随机过程在金融中的应用概率论与随机过程是数学的一个分支,也是金融领域中不可或缺的知识。
概率论可以帮助我们理解金融市场的风险与回报关系,随机过程则可以用来模拟金融市场价格的变动。
例如,在期权定价中,我们可以利用随机过程模拟股票价格的变动情况,进而确定期权的价格。
六、数学优化在经济规划中的应用数学优化是一门研究如何寻找最优解的学科,也是经济规划中的重要工具。
数学优化可以帮助我们在有限资源下,实现最大化利润或最小化成本。
例如,在生产计划中,我们可以利用数学优化的方法确定最佳的生产量和资源配置方案。
数理金融基础1
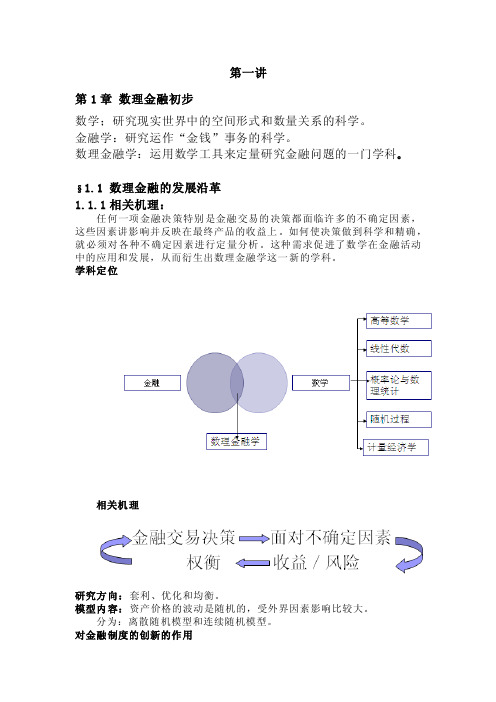
第一讲第1章数理金融初步数学;研究现实世界中的空间形式和数量关系的科学。
金融学:研究运作“金钱”事务的科学。
数理金融学:运用数学工具来定量研究金融问题的一门学科。
§1.1 数理金融的发展沿革1.1.1相关机理:任何一项金融决策特别是金融交易的决策都面临许多的不确定因素,这些因素讲影响并反映在最终产品的收益上。
如何使决策做到科学和精确,就必须对各种不确定因素进行定量分析。
这种需求促进了数学在金融活动中的应用和发展,从而衍生出数理金融学这一新的学科。
学科定位相关机理研究方向:套利、优化和均衡。
模型内容:资产价格的波动是随机的,受外界因素影响比较大。
分为:离散随机模型和连续随机模型。
对金融制度的创新的作用1.1.2 数理金融的发展阶段:金融交易过程:实际上是一个以金融产品价格为核心的风险和收益的度量与决策问题,本质上是一个如何把交易行为进行量化并进而研究其相互之间关系的问题。
是数理金融得以产生和发展的现实基础。
I:发展初期(1954-1968).代表人物有,阿罗,德布鲁,马柯维茨,夏普,莫迪利亚等.阿罗——德布鲁均衡理论和资产组合理论II:黄金时代(1969-1979).代表人物有莫顿,布莱克,卢卡斯,哈里森等.历史上第一个期权定价模型:Black-ScholesIII:完善时期(1980-至今) .代表人物有达菲,卡瑞撤斯和考克斯等主要是基于Black-Scholes及其有关的套利模型。
1.1.3 今年来国内数理金融的发展特点:起步晚,研究问题接近世界前沿。
主要方法:鞅论、随机微分方程和随机积分§1.2 数理金融的框架结构:1.2.1 微观金融和宏观金融金融学:研究如何在不确定的环境下,通过资本市场对资源进行跨期最优配置的一门学科。
微观金融:出现在20世纪50年代,主要考虑金融现象的微观基础,研究如何在不确定情况下,通过金融市场对资源进行跨期最优配置。
微观金融的理论目标和主要内容是:实现市场均衡和获得合理金融产品价格体系。
随机过程在金融中的应用8随机积分—Ito积分共65页文档

45、法律的制定是为了保证每一个人 自由发 挥自己 的才能 ,而不 是为了 束缚他 的才能 。—— 罗伯斯 庇尔
ቤተ መጻሕፍቲ ባይዱ
31、只有永远躺在泥坑里的人,才不会再掉进坑里。——黑格尔 32、希望的灯一旦熄灭,生活刹那间变成了一片黑暗。——普列姆昌德 33、希望是人生的乳母。——科策布 34、形成天才的决定因素应该是勤奋。——郭沫若 35、学到很多东西的诀窍,就是一下子不要学很多。——洛克
随机过程在金融中的应用8随 机积分—Ito积分
41、实际上,我们想要的不是针对犯 罪的法 律,而 是针对 疯狂的 法律。 ——马 克·吐温 42、法律的力量应当跟随着公民,就 像影子 跟随着 身体一 样。— —贝卡 利亚 43、法律和制度必须跟上人类思想进 步。— —杰弗 逊 44、人类受制于法律,法律受制于情 理。— —托·富 勒
数学中的随机分析与随机控制

数学中的随机分析与随机控制随机分析和随机控制是数学中重要的分支领域,它们在解决现实生活中的问题时发挥着重要的作用。
本文将为大家介绍数学中的随机分析和随机控制的概念、应用以及相关的数学方法。
一、随机分析随机分析是研究随机过程中的微积分问题的学科,它是对随机过程进行微积分和微分方程理论的推广。
随机过程是一组随机变量的集合,用来描述具有随机变化的现象。
随机分析通过引入随机积分和随机微分等工具,研究随机过程的性质和行为。
随机分析的应用非常广泛。
在金融工程中,随机分析被用于对金融市场中的随机波动进行建模和分析,以及对衍生金融产品价格和风险进行评估。
在物理学中,随机分析被应用于对分子运动、量子力学等随机性现象的建模和分析。
此外,随机分析还在信号处理、控制理论等领域有着重要的应用。
随机分析的数学方法主要包括随机微分方程、随机偏微分方程、随机积分等。
随机微分方程是关于随机过程的微分方程,描述了随机过程的演化规律。
随机偏微分方程则是描述随机过程中随机性的空间分布和时间演化的方程。
二、随机控制随机控制是研究如何通过控制器控制随机过程的学科,它将随机过程理论与控制理论相结合,研究如何通过适当的控制策略调节随机过程的行为,以实现特定的控制目标。
随机控制在工程和自然科学中都有广泛的应用。
在工程控制中,随机控制被用于对不确定性系统的稳定性、鲁棒性以及性能进行分析和设计。
例如,在自动驾驶车辆中,随机控制可以应用于实现车辆的路径规划和轨迹跟踪。
在生态学中,随机控制可以应用于对生态系统的稳定性和恢复性进行研究。
随机控制的数学方法主要包括最优随机控制、随机反馈控制等。
最优随机控制是研究如何选择最优的控制策略,使系统达到预期的性能指标。
随机反馈控制则是通过测量随机过程的状态并反馈到控制器中,实现对随机过程的控制。
三、随机分析与随机控制的关系随机分析和随机控制是紧密相关的学科,它们相互影响、相互促进。
随机分析提供了数学工具和理论基础,用于描述和分析随机过程的行为;而随机控制则将这些理论应用到实际问题中,通过设计和实现控制策略来调节随机过程的行为。
积分学的意义和经济应用

积分学的意义和经济应用Integral calculus is an essential branch of mathematics that dealswith the concepts of areas, volumes, and rates of change. 积分学是数学的一个重要分支,涉及面积、体积和变化率的概念。
It plays a crucial role in various fields such as physics, engineering, economics, and finance. 它在物理学、工程学、经济学和金融学等领域起着至关重要的作用。
One of the primary purposes of integral calculus is to calculate the total accumulation of a quantity over a given interval. 积分学的一个主要目的是计算在给定区间内数量的总积累。
This allows us to find solutions to problems involving continuous change and accumulation, which are common in real-world applications. 这使我们能够找到涉及连续变化和积累的问题的解决方案,这在现实世界的应用中很常见。
In the realm of economics, integral calculus is used to analyze and model various economic phenomena. 在经济领域,积分学被用来分析和建模各种经济现象。
One of the key applications of integral calculusin economics is in the calculation of total revenue, total cost, and profit functions for firms. 积分学在经济学中的一个关键应用是计算公司的总收入、总成本和利润函数。
谈谈我对金融数学的认识

谈谈我对金融数学的认识金融数学是数学与金融学相结合的交叉学科,旨在利用数学工具来描述、建模和分析金融问题。
以下是本人对金融数学的认识,主要包括以下几个方面:一、金融数学概述金融数学是指运用数学方法来研究金融问题,其目的是寻找金融市场的规律和预测未来的趋势。
金融数学的研究范围广泛,包括投资组合优化、衍生品定价、风险管理等方面。
二、金融数学的发展历程金融数学的发展始于20世纪50年代,当时期权定价理论开始发展起来。
随后,越来越多的数学工具被应用于金融领域,如随机过程、随机微分方程等。
随着计算机技术的发展,金融数学在实践中得到了广泛应用,为投资银行、基金公司等金融机构提供了重要的支持。
三、金融数学基础知识金融数学的基础知识包括随机过程与布朗运动、随机积分与随机微分方程、金融市场的数学模型等。
这些知识是理解和分析金融市场的基础。
四、金融衍生品定价理论金融衍生品定价理论是金融数学的核心内容之一,包括欧式期权定价模型、美式期权定价模型和其他衍生品定价模型。
这些模型能够准确地预测衍生品的价值,为投资决策提供了重要的参考。
五、风险管理理论风险管理是金融数学的重要应用之一,包括衡量风险的方法、投资组合优化理论、VaR模型与风险管理等方面。
这些理论和方法可以帮助投资者有效地管理和降低风险。
六、金融数学在实践中的应用金融数学在实践中得到了广泛应用,包括资产定价与投资决策、风险管理实践中的运用等。
通过运用金融数学的方法和模型,投资者可以更加准确地预测市场趋势,优化投资组合,降低风险,提高收益。
同时,金融机构可以利用金融数学的工具来设计创新性的产品和服务,提高市场竞争力。
总之,金融数学是一门涉及多个学科领域的交叉学科,它的发展和应用为金融市场注入了新的活力和动力。
通过学习和掌握金融数学的基本概念、方法和模型,我们可以更好地理解和分析金融市场,为未来的投资和发展提供重要的支持和保障。
随机过程中的随机积分的应用

随机过程中的随机积分的应用随机过程是一种随机变量随时间变化的数学模型,它在自然科学和社会科学中有着广泛的应用。
在随机过程中,随机积分是一种常见的数学工具,在分析随机过程时,经常需要用到随机积分的概念和性质。
本文将介绍随机过程中的随机积分及其应用。
一、随机过程的定义在概率论中,随机过程是指一组随机变量X(t),t∈T,其中T是一个参数集合,随机变量X(t)称为过程在时刻t的值。
参数T可以是有限集合、无限集合、离散集合或连续集合。
二、随机积分的定义随机积分是指在随机过程中,对过程中的函数进行积分的运算。
具体来说,如果f(t)是一个定义在参数集合T上的随机过程,且g(t)是一个确定的函数,则f(t)的随机积分可以表示为:∫g(t)f(t)dt其中t是变量,g(t)是确定的函数,f(t)是随机过程。
三、随机积分的性质随机积分具有很多重要的性质,包括线性性、可加性、均值和方差等。
1.线性性对于任意的随机过程f(t)和确定函数g1(t)和g2(t),有:∫(g1(t)f(t)+g2(t)f(t))dt=∫g1(t)f(t)dt+∫g2(t)f(t)dt即随机积分是线性运算。
2.可加性对于任意的随机过程f(t)和g(t),有:∫(f(t)+g(t))dt=∫f(t)dt+∫g(t)dt即随机积分是可加运算。
3.均值和方差设t1,t2∈T且t1<t2,则f(t)的随机积分的均值和方差分别为:E(∫t1t2f(t)dt)=∫t1t2E(f(t))dtVar(∫t1t2f(t)dt)=∫t1t2∫t1t2Cov(f(s),f(t))dsdt其中E(f(t))和Cov(f(s),f(t))分别表示f(t)的期望值和协方差。
四、随机积分的应用随机积分在随机过程的分析中有着广泛的应用,包括随机微分方程、随机振动、金融工程、信号处理等领域。
下面以随机微分方程为例,介绍随机积分的应用。
随机微分方程是一类涉及随机过程的微分方程,形式为:dx(t)=f(t,x(t))dt+g(t,x(t))dW(t)其中x(t)是一个随机过程,W(t)是一个Wiener过程,随机过程f(t,x(t))和g(t,x(t))分别对应着确定性的漂移项和随机扰动项。
金融数学模型及其应用

金融数学模型及其应用随着金融市场的发展和复杂性的增加,金融数学模型正变得越来越重要。
这些模型基于数学和统计学的原理,可以用来帮助分析金融市场和战略,预测风险和盈利,以及制定有效的投资和风险管理策略。
本文将探讨金融数学模型的几个关键方面,并说明一些实际应用场景。
一、金融数学模型的基础金融数学模型的基础是数学和统计学,其中最常用的工具是微积分、微分方程、概率论和统计学。
在建立一个金融数学模型之前,需要确定一些关键因素,如时间、风险和收益。
这些因素可以用数字和数学公式来表达,统计学方法可以用来帮助分析这些因素的关系。
二、金融数学模型的类型金融数学模型有许多不同的类型,其中许多都基于随机过程。
其中最常用的包括:1. 布朗运动模型:这种模型又称随机游走模型,是建立期权定价模型的基础。
2. 离散时间模型:这种模型基于离散的时间序列,包括差价合约和期权的定价模型。
3. 连续时间模型:这种模型将价格的变化视为连续的,可以用来分析期权、利率衍生品和其他金融衍生品的定价。
4. 随机波动率模型:这种模型考虑到波动率的变化对价格的影响,用来分析波动率的变化和期权的价格。
5. 蒙特卡洛模拟模型:这种模型不是基于精确公式计算,而是通过随机模拟生成数据,用来分析金融产品的风险和收益。
三、金融数学模型的应用金融数学模型可以应用于多个领域,包括风险管理、投资、保险和买卖。
以下是几个典型的实际应用场景:1. 期权定价模型:这种模型可以用来计算期权的价格,包括欧式期权和美式期权。
期权定价模型可以帮助投资者确定什么时候买入或卖出期权,以及价格的影响因素。
2. 对冲策略:对冲是一种利用金融衍生品来降低风险的策略。
金融数学模型可以用来确定对冲策略,以降低投资组合的波动性。
3. 风险管理:金融数学模型可以用来确定股票、债券和其他金融资产的风险水平。
这些风险可以通过金融衍生品和对冲策略进行管理。
4. 预测:金融数学模型可以用来分析市场和产品的走势,以帮助投资者预测未来价格的变化。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
从随机积分到数学金融
Yu.KabanovR.LipsterJ.StoyanovFrom Stochastic CalculUS toMathematical Finance2006,633pp.Hardcover EUR 80.00ISBN 3-540-30782-6Springer
数学金融是投资者进行投资决策的理论依据。
它能帮助投资者通过建立模型进行投资分析,以降低投资的风险系数,使投资者获得最大的利益。
数学金融以随机微分学和随机控制理论为基础,是经济学家和经济研究工作者研究经济投资问题的必备工具之一。
该论文集反映了随机微积分发展的最新趋势、数学金融学者及其研究所关注的深层开放的新观点;讨论了随机控制及其在经济、金融和信息理论中的应用。
部分重要论文内容如下:(1)V.Arkin和A.Slasmikov的及时投资优化模型为各种征税方案提供一种方法;(2)Yu.Kabanov和M.kijima
的合作模型为自主产品潜能中的投资和金融市场中投资提
供了一种决策方法;(3)M.Raso-nyi和L.Stettner提出离散时间模型,使投资者正确投资以获得最大的经济利益;
(4)I.Sonin写的论文讨论了去除算法主要是解决可数状态速度Markov链的递归优化问题;(5)O.Bamdorff-Nielsen等五
位学者指出了近似值和极限值的不同;(6)J.Carcov和
J.Stouanov用不同随机调节系数方程描绘双面系统和渐进稳定财产的问题;(7)A.Cherny总结了各种集中方法的性质;(8)B.Delyon,A.Juditsky和R.Liptser建立了过程的适中背离原则经历各种Markov链过程的一致变化,该方法主要工具是泊松方程和随机指数;(9)A.Guschin和D.Zh-danov用统计规律证明了极大极小准则,总结了Haussler分歧函数的结论;
(10)J.Fajardo等几个学生主要致力于研究金融适应性这一关键点上跳跃过程,如J.Fajardo等的筛选放大理论;(11)H.J.Engelbert等认为解决Skorohod问题惟一方法是用零漂移和可计算的扰动计算系数一维随机方程;(12)S.Lototsky 和B.Rozovskii提出了一种新的解决有限或无限扰动方程的方法;(13)M.Mania和R.Tevzadze证明了BMO不等式的解决方法,使数学金融学得到进一步的发展;(14)J.Obloj和M.Yor的论文给出了二维过程和谐函数的特性;(15)G.Peskir 致力于研究偏微分方程用于解决不相似的线性随机方程和
起源积分的基本方法。
论文集还涉及到布朗优化问题、高斯编码和解码的优化结果、经历各种Markov链过程背离原则的变化情况和现代基础方法在金融数据经验研究中的应用
等等。
该论文集有以下几个特点:1该文集中的论文主要是由Albert的早期学生、合著者、同事及其仰慕者所写,以此
来纪念Albert Shiryaev的70岁生日;2论文集提出了很多模型和方法来解决数学金融中所遇到的问题;3将数学理论和随机控制理论应用到金融理论中,经济或金融研究更具有理论基础。
作者R.Lipster是Tel Aviv大学电气工程学院教授,主要研究问题包括过滤问题的近似问题、大规模偏移问题、排队论中的近似扩散、随机控制的近似问题和决策理论等问题;作者J.Stoyanov是Newcastle大学数学统计学院教授,主要研究问题包括随机分析和应用、随机过程论、分布特性、时机问题和随机过程和概率论中的博弈问题。
侯玉梅,教授
(秦皇岛市燕山大学经济管理学院北京理工大学管理与经济学院博士后)
Hou Yumei,Professor(The college of economics and management,
Yanshan University)。
