正态总体均值及方差的假设检验表复习课程
合集下载
8.2-0单正态假设检验

解 这里方差σ2未知,因此检验统计量为
u X 0 . S/ n
拒绝域为| u | u / 2 .查表得 u / 2 = u0.025 = 1.96 .
由于
| u | | x 0 | 0.4 50 1.22 1.96 , s/ n 4
所以接受H0,即认为总体的均值μ=0.
147,150,149,154,152,153,148,151, 155
假设零件长度服从正态分布,问这批零件是否
合格(取 = 0.05)?
解 这里是在总体方差 2 未知的情况下,检验假设 H0: 0 150 ,H1: 150 .
在H0成立时,检验统计量
T X 0 ~ t(n 1) .
| t | | x 0 | 1.096 2.306 .
s/ n
所以接受H0,即认为这批零件合格.
三、正态总体方差的假设检验— 2 检验
设总体 X ~ N (, 2 ) 平 .
, (X1,X2,…,Xn)为X 的样本,给定显著性水
1.当 已知时,方差 2的假设检验
H0: 2
(5)由数据计算得x 112.8, s 1.1358
故T 112.8 112.6 0.4659 2.4469 1.1358 7
故接受H 0 ,即可认为用热敏电阻测温仪间接测量温度无系统 误差。
例2 某车间加工一种零件,要求长度为150mm, 今从一批加工后的这种零件中抽取 9 个,测得长度如 下:
2
2 (n)
或 2
2 1
2 (n)
2
2 0
2
2 0
2
2
u X 0 . S/ n
拒绝域为| u | u / 2 .查表得 u / 2 = u0.025 = 1.96 .
由于
| u | | x 0 | 0.4 50 1.22 1.96 , s/ n 4
所以接受H0,即认为总体的均值μ=0.
147,150,149,154,152,153,148,151, 155
假设零件长度服从正态分布,问这批零件是否
合格(取 = 0.05)?
解 这里是在总体方差 2 未知的情况下,检验假设 H0: 0 150 ,H1: 150 .
在H0成立时,检验统计量
T X 0 ~ t(n 1) .
| t | | x 0 | 1.096 2.306 .
s/ n
所以接受H0,即认为这批零件合格.
三、正态总体方差的假设检验— 2 检验
设总体 X ~ N (, 2 ) 平 .
, (X1,X2,…,Xn)为X 的样本,给定显著性水
1.当 已知时,方差 2的假设检验
H0: 2
(5)由数据计算得x 112.8, s 1.1358
故T 112.8 112.6 0.4659 2.4469 1.1358 7
故接受H 0 ,即可认为用热敏电阻测温仪间接测量温度无系统 误差。
例2 某车间加工一种零件,要求长度为150mm, 今从一批加工后的这种零件中抽取 9 个,测得长度如 下:
2
2 (n)
或 2
2 1
2 (n)
2
2 0
2
2 0
2
2
11-正态总体的假设检验

机地抽取36位考生的成绩,算得平均成绩为66.5分,标 准差为15分,问在显著性水平0.05下,是否可以认为在 这次考试中全体考生的平均成绩为70分?
解: 原假设 H , 备择假设 H 70 0 : μ70 1 :μ
检验统计量: T X μ 0
S n
拒绝域:
W {T t ( 1 ) } α n
2
1n X i μ 0 2 ( ) 是σ2的无偏估计量, 此时,因为 n i1 σ 0 n X 2 i μ 0 2 ( ) 偏小或偏大, 拒绝域应表现为 χ σ i 1 0
2 2 ( X μ ) ( X μ ) i i 2 2 i 1 i 1 P { χ ( n )} P { χ ( n )} α α α 2 2 1 2 2 σ σ 0 0
拒绝域:
2 2 W { χ χ ( n 1 ) } α
2 2 ( n 1 ) χ ( 8 ) 15 . 507 n=9 ,α=0.05, χ α 0 . 05
W{χ215 .507 }
2 ( n 1 ) S χ2 σ2
2 8 0 .007 .507 15 .68 15 2 0 .005
因为
χ 2 W
所以拒绝H0,
即在显著性水平α=0.05下,认为这批导线的标准差显 著地偏大.
三、两个正态总体均值的假设检验
2 ) 的样本, 为取自总体 N ( X , X , , X 1 1 1 2 n 1
2 ) 的样本, 为取自总体 N ( Y , Y , , Y 2 2 1 2 n 2
2
n=36, α=0.05,
t ( n 1 ) t ( 35 ) 2 . 0301 α / 2 0 . 025
解: 原假设 H , 备择假设 H 70 0 : μ70 1 :μ
检验统计量: T X μ 0
S n
拒绝域:
W {T t ( 1 ) } α n
2
1n X i μ 0 2 ( ) 是σ2的无偏估计量, 此时,因为 n i1 σ 0 n X 2 i μ 0 2 ( ) 偏小或偏大, 拒绝域应表现为 χ σ i 1 0
2 2 ( X μ ) ( X μ ) i i 2 2 i 1 i 1 P { χ ( n )} P { χ ( n )} α α α 2 2 1 2 2 σ σ 0 0
拒绝域:
2 2 W { χ χ ( n 1 ) } α
2 2 ( n 1 ) χ ( 8 ) 15 . 507 n=9 ,α=0.05, χ α 0 . 05
W{χ215 .507 }
2 ( n 1 ) S χ2 σ2
2 8 0 .007 .507 15 .68 15 2 0 .005
因为
χ 2 W
所以拒绝H0,
即在显著性水平α=0.05下,认为这批导线的标准差显 著地偏大.
三、两个正态总体均值的假设检验
2 ) 的样本, 为取自总体 N ( X , X , , X 1 1 1 2 n 1
2 ) 的样本, 为取自总体 N ( Y , Y , , Y 2 2 1 2 n 2
2
n=36, α=0.05,
t ( n 1 ) t ( 35 ) 2 . 0301 α / 2 0 . 025
8.3 正态总体方差的假设检验v2Up20140631有推导

25 9200 46 44.314 , 5000
所以拒绝 H 0 , 认为这批电池的寿命的波动性较
以往的有显著的变化.
二、两个正态总体方差的假设检验
设 X 1 , X 2 ,, X n1 为来自正态总体 N ( 1 , 1 )的
2
样本, 设 Y1 ,Y2 ,,Yn1 为来自正态总体 N ( 2 , 2 )的
要使 P{ H 0 为真, 拒绝 H 0 } , 只需令
( n 1) S 2 ( n 1) k P 2 2 . 2 2 0 0
因
( n 1) S
2
2
~ ( n 1),
2
( n 1)k
0
2
( n 1)
2
2 1 / 2
2
( n 1)
2 0.99
( 25) 11.52,
0 5000, 由(3.1)拒绝域为 ( n 1) s 2 ( n 1) s 2 44.31. 11.52, 或 2 2 0 0
由观察值s 9200得
2
( n 1) s
2
0
2
于是得拒绝域为:
( n 1) s
2
0
2
2 1 / 2
( n 1) 或
( n 1) s
2
0
2
2 / 2 ( n 1).
下面来求单边检验问题的拒绝域 ( 设显著水平 为 )
H0 : 0 ,
2 2
H1 : 0 ,
2 2
因H 0中的全部 都比H1中的 要小,
正态总体均值、方差的检验法见下表
第二节 正态总体均值的假设检验8-2

14
三、基于成对数据的检验(t 检验):
设X和Y是两个正态总体, 均值分别为 1 和 2 , X 和 Y不是相互独立的。取成对样本 : (X1 , Y1) , (X2 , Y2) , … , ( Xn , Yn )。 要检验: H0 : 1 = 2 , H1 : 1 ≠ 2 . 可以把这个问题转化成单个总体的假设检验 , 令Z = X - Y , 它服从 N ( , 2) , 这里 (= 1- 2) , 2 均未知。 Zi = Xi – Yi (i=1 , 2 , … , n)是来自该正态总体的样本。 显然 , 检验 H0 : 1= 2 , H1 : 1 ≠ 2 等价于检验 H0 : =0 , H1: ≠0,
11
例 2. 在平炉上进行一项试验以确定改变操作方法的建 议是否会增加钢的得率, 试验是在同一只平炉上进行 的. 每炼一炉钢时除操作方法外, 其它条件都尽可能 做到相同. 先用标准方法炼一炉, 然后用建议的方法 炼一炉, 以后交替进行, 各炼了10炉, 其得率分别为: 标准方法: 78.1 72.4 76.2 74.3 77.4 78.4 新方法: 79.1 76.0 81.0 75.5 76.7 77.3 80.0 77.3 79.1
16
解: 分别作各对数据的差 zi = xi - yi ,如上表 ,
并假设 z1 , z2 , … , z9 来自正态总体N ( , 2 ) ,
这里 , 2 均属未知 。若两台仪器的性能一样, 则各对数据的差异可看作是随机误差, 而随机误差可以认为服从正态分布, 其均值为零, 因此本题归结为检验假设: H0: =0 , H1: ≠ 0. 由前面的结论知,可取 T =
问是否有理由认为元件的平均寿命大于225小时?
解 : 按题意需检验 H 0 : 0 = 225 , H 1 : > 225 . X- 取 a = 0 .05,统计量: t = 。 S n 当 H 0 成立时,由 X - 0 S n X- S n ,
正态总体均值和方差的假设检验

给定检验水平,查t(n-1)表得, t1-/2(n-1),使
得,
P{| T | t (n 1)}
即得,
1 2
P{|
x s
0
|
t 1
(n 1)}
n
2
拒绝域: 即
算出|T|与 t1比较,若 2 否则,接受H 0.
T , t1拒 绝 , H 0 2
例3 在某砖厂生产的一批砖中,随机地抽取6块进 行抗断强度试验,测得结果(单位:kg/cm2)如下: 32.56, 29.66, 31.64, 30.00, 31.87, 31.03, 设砖的抗断强度服从正态分布.问这批砖的 平均抗断强度是否为32.50 (kg/cm2)?(=0.05)。
2 0
,
H1
:
2
2 0
给定检验水平 ,查 2 n 1 分布表得
2 (n 1),
使得 P 2 2 (n 1)
根据样本值计算统计量的值.
如果 2 2 (n 1)
则拒绝 H 0 , 接受 H1.
第一类错误
弃真错误
第二类错误
取伪错误
假设检验的两类错误
所作判断 真实情况
H0 为真 H0 为假
接受 H0
拒绝 H0
正确
第二类错误 (取伪)
第一类错误 (弃真)
正确
犯第一类错误的概率通常记为 犯第二类错误的概率通常记为
P
否定H0
H
为真
0
P第一类错误
P
不否定H0
H
为假
0
P第二类错误
若 T t,1拒绝 ,H接0 受
H1
T t1 ,接受 H,0 拒绝 H。1
3,4形式的检验成为右边检验.
7-2 正态总体均值与方差的假设检验

因为 X ~ N ( , 2 ), 0.15,
要检验假设 H 0 : 10.5, H1 : 10.5,
n 15,
x 10.48,
2
0.05,
x 0 10.48 10.5 0.516, 则 / n 0.15 / 15
查表得 u0.05 1.645,
H1 : 0 10
x 9.2
s 1.6
x 0 9.2 10 于是 T 3.54 2.01 t0.025 49 s n 1.6 50
故在 0.05 的水平下,丰产林的树高与10米的差异 有统计意义。(拒绝原假设)
例7 某车间生产某种化学纤维的强度服从正态分布,且原来
单边检验
2
得H0 的拒绝域为:
2 n 1 S 2 0
12 n
或
2 n 1 S 2 0
2 n
作业
• 习题七:3,5,9,12.
• 复习第七章(可做习题七之1~13题) • 复习5~7章,准备课堂测验
例5 P160 8 从某批矿砂中,抽取容量为 5 的一个样本,测得其 含镍量为(单位:%) 3.25 3.27 3.24 3.26 3.24 设测量值服从正态分布,问在 这批矿砂的含镍量为 3.25 ?
例1 某切割机在正常工作时, 切割每段金属棒的平 均长度为10.5cm, 标准差是0.15cm, 今从一批产品中 随机的抽取15段进行测量, 其结果如下(单位:cm) 10.4 10.6 10.1 10.4 10.5 10.3 10.3 10.2 10.9 10.6 10.8 10.5 10.7 10.2 10.7 假定切割的长度X服从正态分布, 且标准差没有 变化, 试问该机工作是否正常? ( 0.1) 解
要检验假设 H 0 : 10.5, H1 : 10.5,
n 15,
x 10.48,
2
0.05,
x 0 10.48 10.5 0.516, 则 / n 0.15 / 15
查表得 u0.05 1.645,
H1 : 0 10
x 9.2
s 1.6
x 0 9.2 10 于是 T 3.54 2.01 t0.025 49 s n 1.6 50
故在 0.05 的水平下,丰产林的树高与10米的差异 有统计意义。(拒绝原假设)
例7 某车间生产某种化学纤维的强度服从正态分布,且原来
单边检验
2
得H0 的拒绝域为:
2 n 1 S 2 0
12 n
或
2 n 1 S 2 0
2 n
作业
• 习题七:3,5,9,12.
• 复习第七章(可做习题七之1~13题) • 复习5~7章,准备课堂测验
例5 P160 8 从某批矿砂中,抽取容量为 5 的一个样本,测得其 含镍量为(单位:%) 3.25 3.27 3.24 3.26 3.24 设测量值服从正态分布,问在 这批矿砂的含镍量为 3.25 ?
例1 某切割机在正常工作时, 切割每段金属棒的平 均长度为10.5cm, 标准差是0.15cm, 今从一批产品中 随机的抽取15段进行测量, 其结果如下(单位:cm) 10.4 10.6 10.1 10.4 10.5 10.3 10.3 10.2 10.9 10.6 10.8 10.5 10.7 10.2 10.7 假定切割的长度X服从正态分布, 且标准差没有 变化, 试问该机工作是否正常? ( 0.1) 解
数理统计与管理课件 (9)

(3)对于给定的显著性水平α=0.05 ,查标准正态分布表 z z0.025 1.96
2
(4)计算统计量观察值 (5)结论
x 0 1637 1600 z 1.258 n 150 26
z 1.258 z 1.96
2
接受原假设H0
即不能否定这批产品该项指标为1600。
X 0 对于给定的显著性水平α=0.05 , S n 查t分布表得 t (n 1) t0.05 (8) 1.8595
S பைடு நூலகம்0 .3
t
由题意, x 62 .5
计算统计量观察值
x 0 62.5 62.0 5 S n 0.3 9
由于
t 5 t (n 1) 1.8595
X 0 选取统计量 Z n
查标准正态分布表
对于给定的显著性水平α=0.05 ,
z z0.05 1.645
已知n=9,σ=3, x 13.5 计算统计量观察值 x 0 13.5 15.5 z 2 n 3 9 由于 z 2 z 1.645 所以拒绝原假设H0,而接受H1, 即说明用新方法所需时间比用老方法所需时间短。
(2) H0:μ= μ0,H1:μ>μ0;检验规则为 X 0 当 T t (n 1) 时,拒绝H0 S n
当 T X 0 t (n 1) 时,接受H0 S n (3) H0:μ= μ0,H1:μ<μ0;检验规则为
X 0 当 T t (n 1) 时,拒绝H0 S n X 0 当 T t (n 1) 时,接受H0 S n
(2) H0:μ= μ0,H1:μ>μ0;检验规则为 X 0 当 Z z 时,拒绝H0 n
正态分布总体的区间估计与假设检验汇总表
(单侧检验)
2
(n
1)S 2
2 0
~2n1
2
2 /2
n
1
或
2
2 1- / 2
n 1
2 2 n 1
2
≥
2 0
2
<
2 0
(单侧检验)
2
2 1-
n
1
2. 两个正态总体均值及方差的假设检验表(显著性水平 α)
条件 原假设 H0 备择假设 H1
检验统计量
拒绝域
12
,
2 2
已知
1 =2 1 2 1 2
1 2
1 2
(单侧检验)
SW
(n1 1)S12 (n2 1)S22 n1 n2 2
T < - t (n1 n2 2)
1,2
未知
2 1
=
2 2
2 1
≤
2 2
2 1
≠
2 2
(双侧检验)
2 1
>
2 2
(单侧检验)
F
S12 S22
~
F ( n1 - 1, n2 - 1)
F ≥ F /2 n1 1, n2 1
已知
0 / n
X
0 n
u
/2,
X
0 n
u
/2
2 未知 T X 0 ~ t(n 1) S/ n
X
S n 1
t / 2
n
1 ,
X
S n
1
t
/
2
n
1
方差 2
未知
2
(n 1)S 2
2 0
~2n1
(n 2 /
1)S 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
U≥
a1≥a2
a1<a2
U≤-
= 未知
a1=a2
a1≠a2
|T|≥
a1≤a2
a1>a2
T≥
a1≥a2
a1<a2
T≤-
单正态总体均值及方差的区间估计(置信度1-α)
待估参数
条件
检验统计量
拒绝域
均值a
已知
N(0,1)
未知
方差
a=a0已知
a未知
2个正态总体均值差及方差比的区间估计(置信度1-α)
待估参数
条件
正态总体均值及方差的假设检验表
正态总体均值及方差的假设检验表:
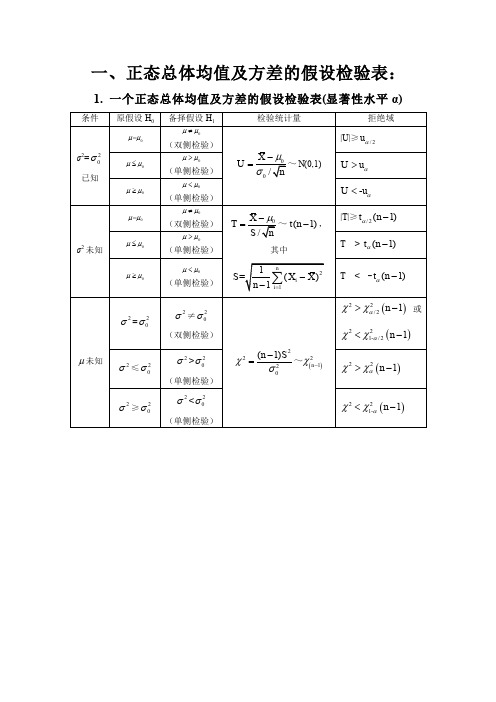
单正态总体均值及方差的假设检验表(显著性水平α)
条件Hale Waihona Puke 原假设H0备择假设H1
检验统计量
拒绝域
σ2= 已知
a=a0
a≠a0
N(0,1)
|U|≥
a≤a0
a>a0
U≥
a≥a0
a<a0
U≤-
σ2未知
a=a0
a≠a0
|T|≥
a≤a0
a>a0
T≥
a≥a0
T≥
a1≥a2
a1<a2
T≤-
a1,a2已知
=
≠
或
≤
>
≥
<
a1,a2未知
=
≠
或
≤
>
≥
<
2个配对样本正态总体均值的假设检验表(显著性水平α)
Z=ξ-η~N(a1-a2, + ),Zi=ξi-ηi.
条件
原假设H0
备择假设H1
检验统计量
拒绝域
, 已知
a1=a2
a1≠a2
N(0,1)
|U|≥
a1≤a2
a1>a2
检验统计量
拒绝域
均值a1-a2
, 已知
N(0,1)
= 未知
方差
a1,a2已知
a1,a2未知
, , .
a<a0
T≤-
a=a0已知
=
≠
或
≤
>
≥
<
a未知
=
≠
或
≤
>
≥
<
2个正态总体均值及方差的假设检验表(显著性水平α)
条件
原假设H0
备择假设H1
检验统计量
拒绝域
, 已知
a1=a2
a1≠a2
N(0,1)
|U|≥
a1≤a2
a1>a2
U≥
a1≥a2
a1<a2
U≤-
= 未知
a1=a2
a1≠a2
,
|T|≥
a1≤a2
a1>a2
a1≥a2
a1<a2
U≤-
= 未知
a1=a2
a1≠a2
|T|≥
a1≤a2
a1>a2
T≥
a1≥a2
a1<a2
T≤-
单正态总体均值及方差的区间估计(置信度1-α)
待估参数
条件
检验统计量
拒绝域
均值a
已知
N(0,1)
未知
方差
a=a0已知
a未知
2个正态总体均值差及方差比的区间估计(置信度1-α)
待估参数
条件
正态总体均值及方差的假设检验表
正态总体均值及方差的假设检验表:
单正态总体均值及方差的假设检验表(显著性水平α)
条件Hale Waihona Puke 原假设H0备择假设H1
检验统计量
拒绝域
σ2= 已知
a=a0
a≠a0
N(0,1)
|U|≥
a≤a0
a>a0
U≥
a≥a0
a<a0
U≤-
σ2未知
a=a0
a≠a0
|T|≥
a≤a0
a>a0
T≥
a≥a0
T≥
a1≥a2
a1<a2
T≤-
a1,a2已知
=
≠
或
≤
>
≥
<
a1,a2未知
=
≠
或
≤
>
≥
<
2个配对样本正态总体均值的假设检验表(显著性水平α)
Z=ξ-η~N(a1-a2, + ),Zi=ξi-ηi.
条件
原假设H0
备择假设H1
检验统计量
拒绝域
, 已知
a1=a2
a1≠a2
N(0,1)
|U|≥
a1≤a2
a1>a2
检验统计量
拒绝域
均值a1-a2
, 已知
N(0,1)
= 未知
方差
a1,a2已知
a1,a2未知
, , .
a<a0
T≤-
a=a0已知
=
≠
或
≤
>
≥
<
a未知
=
≠
或
≤
>
≥
<
2个正态总体均值及方差的假设检验表(显著性水平α)
条件
原假设H0
备择假设H1
检验统计量
拒绝域
, 已知
a1=a2
a1≠a2
N(0,1)
|U|≥
a1≤a2
a1>a2
U≥
a1≥a2
a1<a2
U≤-
= 未知
a1=a2
a1≠a2
,
|T|≥
a1≤a2
a1>a2
