普通物理力学例题总结
物理力学练习题20篇及解析

液体压强计探究液体压强特点,B 符合题意;
C. 惯性是物体的基本属性,与是否重重力无关,所以在太空失重情况下可以探究物体是否
具有惯性,C 不符合题意;
D. 物体间力的作用是相互的,是力的基本特征,与是否受到重力无关,所以在太空失重情
况下可以进行探究,D 不符合题意;
故答案为:B。
【分析】液体由于重力,对液体内部有压强,在失去重力的作用时不能再进行实验.
非平衡力的作用,D 不符合题意,
故答案为:A。
【分析】二力平衡的条件:作用在同一物体上的两个力,如果大小相等、方向相反、并且
在同一直线上,则这两个力二力平衡时合力为零.
物体间力的作用是相互的. (一个物体对别的物体施力时,也同时受到后者对它的力).
4.在如图所示实验中,将小铁球从斜面顶端由静止释放,观察到它在水平桌面上运动的轨 迹如图甲中虚线 OA 所示。在 OA 方向的侧旁放一磁铁,再次将小铁球从斜面顶端由静止释 放,观察到它在水平桌面上运动的轨迹如图乙中虚线 OB 所示。由上述实验现象可以得出 的结论是( )
2.下列说法错误的是( )
A. 足球被踢出后仍继续向前运动,是因为它运动时产生惯性 B. 汽车在转弯时减速是为
了防止惯性带来的危害
C. 闻到花香说明分子在不停地做无规则运动
D. 游泳时向后划水,人向前运动,是因
为物体间力的作用是相互的
【答案】A
【解析】【解答】A、足球被踢出后仍继续向前运动,是因为它具有惯性,不能说“产生惯
物理力学练习题 20 篇及解析
一、力学
1.下列关于力的说法中,错误的是( ) A.人推车时,人也受到车给人的推力 B.两个物体只要互相接触,就一定发生力的作用 C.用手捏一个空易拉罐,易拉罐变瘪了,表明力可以使物体发生形变 D.排球运动员扣球使球的运动方向发生了改变,表明力可以改变物体的运动状态 【答案】B 【解析】 力是物体对物体的作用,物体间力的作用是相互的;力的作用效果有两个,一是改变物体 的形状,二是改变物体的运动状态.因为物体间力的作用是相互的,所以人推车时车也推 人,故 A 正确;两个物体即使相互接触,但是如果不相互挤压,也不会发生力的作用,故 B 不正确;用手捏易拉罐,易拉罐瘪了,说明力改变了物体的形状,故 C 正确;扣球使球 的运动方向发生改变,说明力改变了物体的运动状态,故 D 正确,故符合题意的是 B.
高中物理 20个力学经典计算题汇总及解析

高中物理 20个力学经典计算题汇总及解析1. 概述在力学领域中,经典的计算题是学习和理解物理知识的重要一环。
通过解题,我们能更深入地了解力学概念,提高解决问题的能力。
在本文中,我将为您带来高中物理领域中的20个经典力学计算题,并对每个问题进行详细解析,以供您参考和学习。
2. 一维运动1) 题目:一辆汽车以30m/s的速度行驶,经过10秒后匀减速停下,求汽车减速的大小和汽车在这段时间内行驶的距离。
解析:根据公式v=at和s=vt-0.5at^2,首先可求得汽车减速度a=3m/s^2,然后再求出汽车行驶的距离s=30*10-0.5*3*10^2=150m。
3. 二维运动2) 题目:一个质点在竖直平面内做抛体运动,初速度为20m/s,抛体初位置为离地30m的位置,求t=2s时质点的速度和所在位置。
解析:首先利用v=vo+gt求得t=2s时的速度v=20-9.8*2=-19.6m/s,然后再利用s=s0+vo*t-0.5gt^2求得t=2s时的位置s=30+20*2-0.5*9.8*2^2=30+40-19.6=50.4m。
1. 牛顿运动定律3) 题目:质量为2kg的物体受到一个5N的力,求物体的加速度。
解析:根据牛顿第二定律F=ma,可求得物体的加速度a=5/2=2.5m/s^2。
2. 牛顿普适定律4) 题目:一个质量为5kg的物体受到一个力,在10s内速度从2m/s 增加到12m/s,求物体受到的力的大小。
解析:利用牛顿第二定律F=ma,可求得物体受到的力F=5*(12-2)/10=5N。
3. 弹力5) 题目:一个质点的质量为4kg,受到一个弹簧的拉力,拉力大小为8N,求弹簧的弹性系数。
解析:根据弹簧的胡克定律F=kx,可求得弹簧的弹性系数k=8/0.2=40N/m。
4. 摩擦力6) 题目:一个质量为6kg的物体受到一个10N的水平力,地面对其的摩擦力为4N,求物体的加速度。
解析:首先计算摩擦力是否达到最大值f=μN=6*10=60N,由于摩擦力小于最大值,所以物体的加速度a=10-4/6=1m/s^2。
初中物理力学经典例题15道题

初中物理力学经典例题15道题1. 一个质量为2kg的物体,在水平地面上受到10N的水平拉力,求物体的加速度。
解答:根据牛顿第二定律,物体的加速度等于合外力除以物体的质量。
所以物体的加速度为a = F/m = 10N / 2kg = 5m/s^2。
2. 一个质量为0.5kg的物体受到一个5N的竖直向下的重力,求物体的重力加速度。
解答:重力加速度是指物体在自由下落时垂直于地面的加速度。
根据牛顿第二定律,物体的重力加速度等于重力除以物体的质量。
所以物体的重力加速度为g = F/m = 5N / 0.5kg = 10m/s^2。
3. 一个质量为4kg的物体,向右运动时受到一个10N的水平拉力和一个8N的水平推力,求物体的加速度。
解答:物体的加速度等于合外力除以物体的质量。
合外力等于水平拉力减去水平推力,即F = 10N - 8N = 2N。
所以物体的加速度为a = F/m = 2N / 4kg = 0.5m/s^2。
4. 一个质量为2kg的物体,在斜面上受到一个与斜面垂直的力为10N的重力和一个沿斜面方向的力为4N,斜面的倾角为30度,求物体的加速度。
解答:首先将斜面上的力分解为与斜面垂直方向的力和沿斜面方向的力,即重力沿斜面方向的分力为F1 = mg * sinθ,沿斜面方向的合力为F2 = mg * cosθ。
其中,m = 2kg,g = 9.8m/s^2,θ = 30°。
所以沿斜面方向的合力为F2 = 2kg * 9.8m/s^2 * cos(30°) ≈ 16.96N。
物体的加速度等于沿斜面方向的合力除以物体的质量,即a = F2/m = 16.96N / 2kg ≈ 8.48m/s^2。
5. 一个质量为3kg的物体,向左运动时受到一个3N的水平拉力和一个5N的水平推力,求物体的加速度。
解答:物体的加速度等于合外力除以物体的质量。
合外力等于水平推力减去水平拉力,即F = 5N - 3N = 2N。
初中物理力学题集锦

初中物理力学题集锦1. 一个质量为5kg的物体静止在水平面上,受到10N的水平拉力作用,求物体的加速度。
(g取10m/s²)2. 一物体从20m高处自由下落,求落地时的速度和下落时间。
(忽略空气阻力,g=10m/s²)3. 质量为2kg的物体沿光滑斜面下滑,斜面倾角30°,求物体下滑的加速度。
(g取10m/s²)4. 一物体沿直线以5m/s的速度匀速运动,经5秒后速度变为15m/s,求此过程中的加速度。
5. 一轻绳绕过定滑轮两端各挂一质量分别为m1=3kg和m2=2kg 的物体,求m1的加速度。
(不计滑轮摩擦及绳重)6. 一辆汽车以20m/s的速度行驶,紧急刹车后在5秒内停止,求汽车的平均减速度。
7. 一质点做初速度为零的匀加速直线运动,第3秒末的速度为6m/s,求前5秒内的位移。
8. 一物体在水平面上受摩擦力f=10N作用,其与地面的动摩擦因数μ=0.2,求作用在物体上的正压力。
9. 一物体自高h=20m处自由落下,同时另一物体从地面以v0=20m/s的速度竖直上抛,求两物体在空中的相遇时间。
10. 一质量m=2kg的物体置于光滑水平面上,受一恒力F=20N作用,求物体在2秒内的位移。
11. 一斜面长L=10m,高h=5m,一物体无初速度沿斜面下滑,求物体滑到斜面底端时的速度。
(忽略摩擦,g=10m/s²)12. 一质点做匀速圆周运动,半径r=2m,周期T=4s,求质点的线速度和向心加速度。
13. 一物体在水中匀速下沉,若其体积V=0.01m³,密度ρ物=2500kg/m³,水的密度ρ水=1000kg/m³,求物体所受浮力。
14. 一轻弹簧原长l0=0.2m,当挂一质量m=0.5kg的物体时伸长至l=0.25m,求该弹簧的劲度系数k。
15. 一质量为m的物体以初速度v0沿光滑斜面向上滑行,斜面倾角θ=30°,求物体上升的最大高度。
初中物理力学经典例题

初中物理力学经典例题以下是一些经典的初中物理力学例题:1. 一个质量为5kg的物体静止在水平地面上,施加一个10N的水平力。
求物体的加速度。
解答:根据牛顿第二定律F = ma,其中F是物体所受的合力,m是物体的质量,a是物体的加速度。
由于力和质量已知,将其代入方程可以求得加速度。
所以a = F / m = 10N / 5kg = 2m/s²。
2. 一个弹簧常数为200N/m的弹簧拉伸10cm后,求弹簧所受的弹力。
解答:根据胡克定律F = kx,其中F是弹簧所受的弹力,k是弹簧的弹簧常数,x是弹簧的伸长量。
由于弹簧常数和伸长量已知,将其代入方程可以求得弹力。
所以F = 200N/m × 0.1m = 20N。
3.一个物体以2m/s的速度沿直线运动,经过5s后速度变为8m/s。
求物体的加速度。
解答:根据加速度的定义a = (vf - vi) / t,其中a是物体的加速度,vf是物体的最终速度,vi是物体的初始速度,t是时间间隔。
由于初始速度、最终速度和时间间隔已知,将其代入方程可以求得加速度。
所以 a = (8m/s - 2m/s) / 5s = 1.2m/s²。
4. 一个质量为2kg的物体以10m/s的速度水平地撞击到静止的墙壁,反弹后以8m/s的速度反向运动。
求撞击过程中墙壁对物体的平均力。
解答:由于撞击过程中物体速度发生了变化,需要用动量定理来求解。
根据动量定理FΔt = Δmv,其中F是力,Δt是撞击时间,Δm是物体的质量变化量,v是物体的速度变化量。
由于质量变化量为零(质量不变),而速度变化量已知,可以求得撞击时间。
所以Δt = Δmv / F = (2kg × (8m/s - (-10m/s))) / (8m/s) = 9.5s。
由于撞击过程是瞬间发生的,可以认为撞击时间非常短,近似为0。
因此,墙壁对物体的平均力可以近似为墙壁对物体的瞬时力,即F = Δmv / Δt = 2kg × (8m/s - (-10m/s)) / 0s = ∞(无穷大)。
(完整版)高一物理力学典型例题
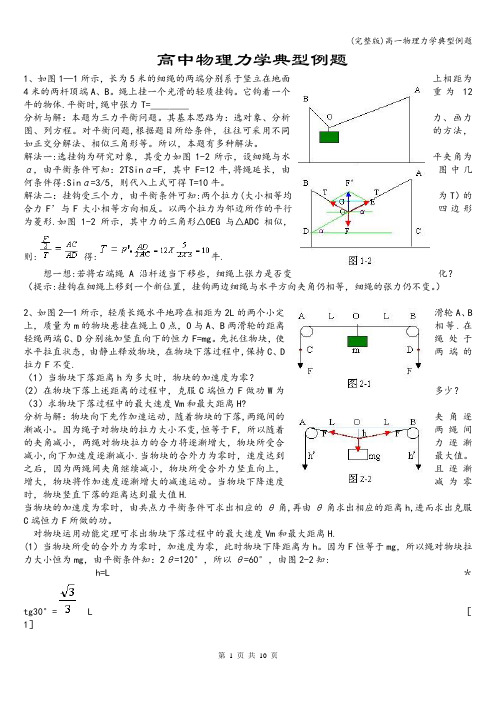
高中物理力学典型例题1、如图1—1所示,长为5米的细绳的两端分别系于竖立在地面上相距为4米的两杆顶端A、B。
绳上挂一个光滑的轻质挂钩。
它钩着一个重为12牛的物体.平衡时,绳中张力T=____分析与解:本题为三力平衡问题。
其基本思路为:选对象、分析力、画力图、列方程。
对平衡问题,根据题目所给条件,往往可采用不同的方法,如正交分解法、相似三角形等。
所以,本题有多种解法。
解法一:选挂钩为研究对象,其受力如图1-2所示,设细绳与水平夹角为α,由平衡条件可知:2TSinα=F,其中F=12牛,将绳延长,由图中几何条件得:Sinα=3/5,则代入上式可得T=10牛。
解法二:挂钩受三个力,由平衡条件可知:两个拉力(大小相等均为T)的合力F’与F大小相等方向相反。
以两个拉力为邻边所作的平行四边形为菱形.如图1-2所示,其中力的三角形△OEG与△ADC相似,则:得:牛.想一想:若将右端绳A 沿杆适当下移些,细绳上张力是否变化?(提示:挂钩在细绳上移到一个新位置,挂钩两边细绳与水平方向夹角仍相等,细绳的张力仍不变。
)2、如图2—1所示,轻质长绳水平地跨在相距为2L的两个小定滑轮A、B 上,质量为m的物块悬挂在绳上O点,O与A、B两滑轮的距离相等.在轻绳两端C、D分别施加竖直向下的恒力F=mg。
先托住物块,使绳处于水平拉直状态,由静止释放物块,在物块下落过程中,保持C、D两端的拉力F不变.(1)当物块下落距离h为多大时,物块的加速度为零?(2)在物块下落上述距离的过程中,克服C端恒力F做功W为多少?(3)求物块下落过程中的最大速度Vm和最大距离H?分析与解:物块向下先作加速运动,随着物块的下落,两绳间的夹角逐渐减小。
因为绳子对物块的拉力大小不变,恒等于F,所以随着两绳间的夹角减小,两绳对物块拉力的合力将逐渐增大,物块所受合力逐渐减小,向下加速度逐渐减小.当物块的合外力为零时,速度达到最大值。
之后,因为两绳间夹角继续减小,物块所受合外力竖直向上,且逐渐增大,物块将作加速度逐渐增大的减速运动。
(完整版)初中物理力学经典例题(带解析)

初中物理力学经典例题(带解析)一、单选题(共11题;共22分)1.如右图用同样的滑轮组分别提起质量相等的一个物体和两个物体,比较甲、乙两图,正确表示机械效率关系的是( )A. η甲=η乙B. η甲<η乙C. η甲>η乙D. 无法比较2.甲物体放在光滑的水平面上,乙物体放在粗糙的水平面上,它们分别在相等的水平力F作用下移动相等的距离s,那么,力F对两物体所做的功( )A. 甲较多B. 乙较多C. 相等D. 无法确定3.下列生活实例中,对图片描述正确的有( )A. 甲图:不计阻力及能量损耗,网球从刚击球拍到球拍形变最大过程中,网球机械能守恒B. 乙图:铁锁来回摆动最终停下,在铁锁下降过程中,重力势能全部转化为动能C. 丙图:人造地球卫星由于不受空气阻力,只有动能和势能的转化D. 丁图:运动员从高处落下,动能转化为重力势能4.如图所示,轻质杠杆AB可绕O点转动,当物体C浸没在水中时杠杆恰好水平静止,A、B两端的绳子均不可伸长且处于张紧状态。
已知C是体积为1dm3、重为80N的实心物体,D是边长为20cm、质量为20kg 的正方体,OA:OB=2:1,圆柱形容器的底面积为400cm2(g=10N/kg),则下列结果不正确的是()A. 物体C的密度为8×103kg/m3B. 杠杆A端受到细线的拉力为70NC. 物体D对地面的压强为1.5×103PaD. 物体C浸没在水中前后,水对容器底的压强增大了2×103Pa5.汽车在平直公路上以速度v匀速行驶,发动机功率为P,牵引力为F0 ,t1时刻开始,司机减小了油门,使汽车保持恒定功率所行驶,到t2时刻,汽车又开始做匀速直线运动,速度为v.已知运动过程中汽车所受阻力f恒定不变,汽车牵引力F随时间t变化的图像如图所示,则()v0A. t1至t2时间内,汽车做加速运动B. F0=2fC. t1时刻之后,汽车将保持功率P0行驶D. v= 126.质量相同的甲、乙两实心金属球密度之比为3:2,将甲球浸没在液体A中,乙球浸没在液体B中,A、B 两种液体的密度之比为5:4,则此时甲、乙两球所受浮力之比为()A. 6:5B. 5:6C. 8:15D. 15:87.小华同学利用如图所示的装置提起水中的物块,下列判断正确的()A. 装置中的滑轮是定滑轮B. 装置中的AOB是省力杠杆C. 物块在上表面露出水面前,所受浮力不断减小D. 该滑轮的机械效率可以达到100%8.实心正方体木块(不吸水)漂浮在水上,如图所示,此时浸入水中的体积为6×10﹣4m3,然后在其上表面放置一个重4N的铝块,静止后木块上表面刚好与水面相平(g取10N/kg,ρ水=1.0×103kg/m3)则该木块()A. 未放置铝块前,木块受到的浮力是10NB. 放置铝块后,木块排开水的体积是1×10﹣3m3C. 木块的密度是0.7×103kg/m3D. 放置铝块后,木块下表面受到水的压强增大了600Pa9.下列涉及压强知识说法不正确的是()A. 海绵块的形变显示了压力作用效果B. 用微小压强计可以研究液体压强C. 托里拆利实验可以测出大气压值D. 船闸不是连通器10.如图所示,用6N的水平拉力F拉动物体A在水平地面上向右匀速运动,物体B静止不动,弹簧测力计示数为2N,下列说法正确的是()A. A对B的摩擦力大小为4N,方向水平向右B. B对A的摩擦力大小为2N,方向水平向右C. 地面对A的摩擦力大小为4N,方向水平向左D. 地面对A的摩擦力大小为6N,方向水平向左11.重力相同的a、b两件货物在两台吊车钢索的牵引下竖直向上运动,它们运动的s—t图像分别如图甲、乙所示,则在图像描述的运动过程中()A. 它们都做匀速直线运动B. a货物所受重力和钢索对它的牵引力是一对作用力与反作用力C. b货物所受重力和钢索对它的牵引力是一对平衡力D. 前6s内,a货物运动的平均速度小于b货物运动的平均速度二、填空题(共2题;共6分)12.在斜面上将一个重600N的物体匀速拉到高处,沿斜面向上的拉力F=400N,拉动的距离s=4.5m,提升高度h=1.8m,所用时间t=30s。
普通物理力学例题总结

r
求解
解 II: 绳某点 r 的张力可理解为此点以外各小段分别所受向心力的 代数和。 T(r) m 微元 r: m r
L
r
m T(r) r ω 2 ri Mω 2 L i L
r
m 2 f(ri ) ω r L
r+r
ri
r
L
r 0
T (r )
L r
dv mg kv m dt
(5) 解方程: 分离变量
dv x k dt vx m
1 dt mg kv y m dv y
分别积分
dt v x dv t k x v x0 v x 0 mdt
k v y0 mg kv y 0 m dt
vy t
m
dv y
mg kv y
kdv y
得
v x v0 cos e m t m mg k v y (v 0 sin g) e k k
kt m
再次积分
x
x0
dx
t
0
v x dt
y
y
得
mv0 cos x (1 e ) k k t mv0 sin m 2 g mg m y( ) (1 e ) t k k k
x=2t 例 1:已知运动方程 求 v (t ) 及 1 秒时的速率 2 y=t
dx dy 解: v (t ) i j 2i 2tj
dt dt 1秒时的速度:v t 1 2i 2 j 1秒时的速率 v v 22 22 2 2
r r r0
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
r
N
mg
mr2
mgsin mr cos 0 r 2 dz r 2 tg g dr g
2
积分
z0
z
dz
0
r
r r dr z z 0 g 2g 抛物线方程
k t m
y0
dy
v
t 0
dt
消去 t ,得轨道方程:
mg m2 g kx x 2 ln 1 y tan kv0 cos mv 0 cos k
例 4:一根不可伸长的轻绳跨过固定在 O 点的水平光滑细杆,两 端各系一个小球。a 球放在地面上,b 球被拉到 lb b 水平位置,且绳刚好伸直。从这时开始将 b 球 O 自静止释放。设两球质量相同。 求:(1) b 球下摆到与竖直线成 角时的 v ; a (2) = ? a 球刚好离开地面。 解: B的运动:a 球离开地面前 b 做半径为 lb 的竖直圆周运动。 (1) v2 lb b O 选自然坐标系列分量方程: Fn T mg cos m lb dv T Ft mg sin m 由切向方程式得: dt N T v dv dv dv d a g sin mg dt d dt lb d
x
t
t
1 4 x t 2t 3 6
例:己知一质点按顺时针方向沿半径为R 的圆周运动。 1 其路程与时间关系为S V t b t 2 0 、b 为常数) (V
0
,此时质点己沿圆周运行了多少圈? (2) t =? 时, a b
(3) 质点何时开始逆时针方向运动? v2 解: an R (1) a at an dv d 2 s at 2 dt dt
mg
x
0
2
( mg kx )dx mvdv
v 0
2 1 2 v ( mgx kx ) m 2
x
例3:有阻力的抛体问题:质量为 m 的炮弹,以初速度 v0 与水平 方向成仰角 射出。 若空气阻力与速度成正比,即 f kv 求: 运动轨道方程 y(x)= ? y 解: 二维空间的变力情况。 f=-kv (1) 选 m 为研究物体; v0 m v (2) 建坐标 xoy; x = 0,y = 0 vx 0=v0 cos mg 初始条件:t =0 时 x o vy 0=v0 sin (3) 分析受力 dv x dv m kv x (4) 列方程: mg f m dt dt 分量方程
2
求:x ( t )
dv 解: 由 a dt v t
2 t 0
dv
a dt
v 2
2 3 v t 2 3
0
t
2d 2t
2 3 t t 3
dx v dt
2 3 1 4 dx v dt ( t 2 ) dt t 2t 6 3 0 0 3
分析 M (相对惯性系)运动,水平方向: N sin=M aM 由此解得相对加速度 a'=(m+M)sing / (M+msin2)
1 2 由 l at 2
2l ( m sin2 M ) t ( M m ) sin g
例:水桶以 旋转,求水面形状?
z
解:水面 z 轴对称,选柱坐标系。任选 水面一小质元,其在切线方向静止。 在旋转参考系中,做受力分析: 切线方向:
v
0
vdv ( lb g sin )d
/2
v 2lb g cos
mg
当 (2) a 的受力和运动: T = mg 时,a 球刚好离地。 2lb g cos 1 1 cos mg 由法向方程式得: mg cos m
lb
3
例 5:一匀质细绳,质量 m,长 L,一端固定在 O,另一端有一 质量为 M 的小球,其在光滑水平面上以 绕 O 点旋转。 求: 绳上各点的张力。 解 I: 绳上张力是距 O 点距离 r 的函数: T(r) 隔离物体法分析绳上一小段 dm 的受力 T(r) r T(r+r)
解:以斜面为参考系(非惯性系), N
物体相对于斜面有沿斜面方向的加速度a' 当 m 滑下时,M 加速度方向如图:
aM
maM
分析物体受力 其中 maM 就是惯性力。而 mg 和 N 是真实力。 mgsin+maMcos=ma' 列方程: 沿斜面方向: 垂直于斜面方向:
方向
N-mgcos+maMsin=0
T
r
求解
解 II: 绳某点 r 的张力可理解为此点以外各小段分别所受向心力的 代数和。 T(r) m 微元 r: m r
L
r
m T(r) r ω 2 ri Mω 2 L i L
r
m 2 f(ri ) ω r L
r+r
ri
r
L
r 0
T (r )
L r
O L
M
m 动力学方程: T(r Δr) T(r) dm ω r r ω 2 r L T(r r) T(r) m 2 ω r r 0 dT m ω2 r r L dr L 每点(无限小,m->0)
2
r+r
L r
合张力为0.
m 2 dT T(M) L( L ω r)dr
vy 1 45
0
vx 错误做法:1 秒钟时的速率:
x t 1 2 t 2 y t 1
2
方向: tan Leabharlann y450 v
x
t 1 得出 v 0
x2 + y2 dt
dr d dr 又如: v = = = dt dt
例2:一质点运动函数为 y t 4 2t 2 (SI),求质点的运动轨道
v风地 10i 5 j
y 南风
v风地
45° x
o
10 m/s 15 m/s
v风地 10 5 11.2 m/s
2 2
5 tan 10
= 27°
?考虑:
在不同的参照系, 对同一质点的运动状态进行描述
例:一列车(S 系)相对于地面(S系)作匀速直线运动, 一人在 车厢内运动 。分别在 S、S系分别对其进行描述。 设 t = 0 时,两坐标系原点重合。t 时刻的运动情况如下: 位矢变换关系式:
大小:
a
求: (1) t 时刻, 质点的加速度
2
a ?
an
V0 bt 2
R
at b
V0 bt 4
R
2
b
2
a
at
方向:
an V0 bt 2 arctan arctan a Rb t
o
v .an
m
(2) a b 时
例:雨天一辆客车在水平马路上以 20 m/s 的速度向东 开行,雨滴在空中以 10 m/s 的速度垂直下落。 求:雨滴相对于车厢的速度的大小与方向。 解:已知
v 10 m/s
方向向下
v雨对地 v '雨对车 u车对地 ' v 雨对车 v雨对地 u车对地
v' v u 22.4 (m/s)
V0 bt 4 b 2
R
2
b
V0 t b
1 2 V02 t 时刻路程: S t V0 t bt 2 2b St V02 圈数: N 2 R 4 Rb
(3) 由前面a t = - b 可知, 质点作减速率圆周运动。 当 V 减到 0 值时,质点将终止顺时针转,而 开始逆时针转。此时刻记为 t V0 V V0 bt 0 t b 也正是前求 a = b 的时刻 t 。
r r r0
y
S系
y
S 系 Δr A B Δ r
u
S 相对 S 平动 速度为 u x x
r人 地 r人 车 r车 地
两边微分
位移变换关系式:
A
O
v v u
Δ r0
O
绝对速度=相对速度+ 牵连速度
再对上式求导得 a a
a2
求解…..
例 2:质量为 m 的物体通过不可伸长的轻绳和不记质 量的滑轮与弹簧(弹性系数 k)连接,初始时刻 物体静止,弹簧为原长,让物体自由下落。 求: 物体的速度随位置变化的关系。 解: 列动力学方程: mg - T = ma
T
T = kx
dv dx dv dv mv mg kx m m dx dt dx dt
x=2t 例 1:已知运动方程 求 v (t ) 及 1 秒时的速率 2 y=t
解: v ( t ) dx i dy j 2i 2tj
dt dt 1秒时的速度:v t 1 2i 2 j 1秒时的速率 v v 22 22 2 2
m
dv y
mg kv y
kdv y
得
v x v0 cos e m t m mg k v y (v 0 sin g) e k k
kt m
再次积分
x
x0
dx
t
0
v x dt
y
y
得
mv0 cos x (1 e ) k k t mv0 sin m 2 g mg m y( ) (1 e ) t k k k
