黑龙江省大庆市第四中学2019-2020学年高一下学期期末考试+数学(理)答案
黑龙江省大庆市第四中学2024_2025学年高一地理下学期第一次检测试题
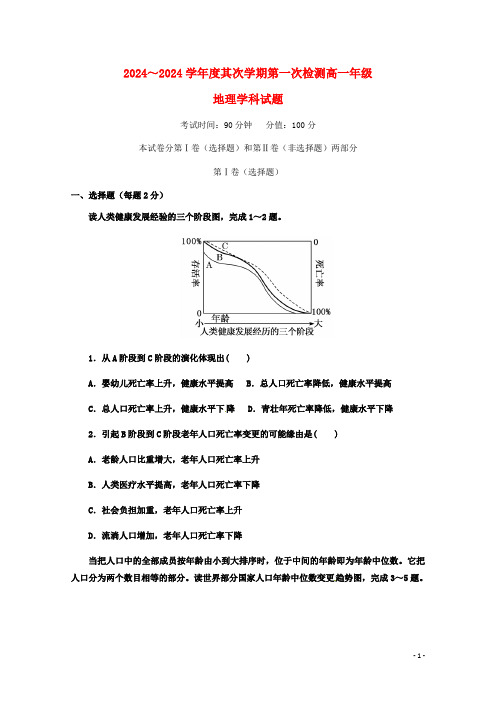
2024~2024学年度其次学期第一次检测高一年级地理学科试题考试时间:90分钟分值:100分本试卷分第Ⅰ卷(选择题)和第Ⅱ卷(非选择题)两部分第Ⅰ卷(选择题)一、选择题(每题2分)读人类健康发展经验的三个阶段图,完成1~2题。
1.从A阶段到C阶段的演化体现出( )A.婴幼儿死亡率上升,健康水平提高 B.总人口死亡率降低,健康水平提高C.总人口死亡率上升,健康水平下降 D.青壮年死亡率降低,健康水平下降2.引起B阶段到C阶段老年人口死亡率变更的可能缘由是( )A.老龄人口比重增大,老年人口死亡率上升B.人类医疗水平提高,老年人口死亡率下降C.社会负担加重,老年人口死亡率上升D.流淌人口增加,老年人口死亡率下降当把人口中的全部成员按年龄由小到大排序时,位于中间的年龄即为年龄中位数。
它把人口分为两个数目相等的部分。
读世界部分国家人口年龄中位数变更趋势图,完成3~5题。
3.上图国家中人口年龄中位数变更最小的是( )A.巴西 B.瑞典 C.俄罗斯 D.中国4.人口年龄中位数主要反映( )A.人口增长数量 B.人口增长速度 C.人口年龄结构 D.人口老龄化程度5.应对中国人口年龄中位数变更趋势的对策不行行的是( )A.激励农村人口增长,解决农村家庭养老问题 B.引入市场机制,发展老龄产业C.完善城镇职工养老保险制度 D.实施“全面二孩”政策生态承载力是指一个国家或地区具有供应可再生资源和汲取二氧化碳实力的土地面积的总和。
如图为一些国家或地区生态承载力的占比图。
读图回答6~7题。
6.导致巴西、俄罗斯生态承载力差异的主要因素是( )A.气候 B.国土面积 C.土壤肥力 D.水资源数量7.下列不能有效提高生态承载力的措施是( )A.提高废水、废气处理率,实现达标排放B.草地开垦C.爱护野生动植物D.防治沙漠化和水土流失榨菜、便利面、火腿肠是流淌人口最为常见的消费品。
如图为某上市公司生产的榨菜在两个地区销售份额占比的变更数据。
2019-2020学年黑龙江省大庆一中高一下学期期末考试数学试题

黑龙江省大庆一中2019-2020学年高一下学期期末考试试题一、选择题1.圆22(1)4x y ++=的圆心坐标和半径分别是( )A .(1,0),2B .(-1,0),2C .(1,0),4D .(-1,0),4 2.等比数列{}n a 中,22a =,514a =,公比q =( ) A .12- B .-2 C .2 D .123.已知向量(,1)a m =,(1,2)b =-,若a b ⊥,则m =( )A .12-B .12C .-2D .24.已知0x >,0y >,且191x y +=,则x y +的最小值为( ) A .12 B .16 C .20 D .245.已知直线1l :(3)10mx m y +-+=,直线2l :(1)10m x my ++-=,若12l l ⊥则m =( )A .0或1B .1C .32-D .0或32- 6.设l 为直线,α,β是两个不同的平面,下列命题中正确的是( )A .若//l α,//l β,则//αβB .若l α⊥,l β⊥,则//αβC .若l α⊥,//l β,则//αβD .若αβ⊥,//l α,则l β⊥7.若变量x ,y 满足约束条件1325x y x x y ≥-⎧⎪≥⎨⎪+≤⎩,则2z x y =+的最大值为( )A .1B .2C .3D .48.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条相互垂直的半径若该几何体的体积是2243π,则它的表面积是( )A .68πB .69πC .70πD .80π9.已知等差数列{}n a 的前n 项和为n S ,若780a a +>,790a a +<则n S 取最大值时n 的值是( )A .4B .5C .6D .710.在空间四边形ABCD 中,已知2AD =,BC =,E ,F 分别是AB ,CD 的中点,EF =,则异面直线AD 与BC 所成角的大小为( ) A .6π B .3π C .4π D .34π 11.已知ABC △中,a ,b ,c 分别为角A ,B ,C 所对的边,且3a =,5b c +=,tan tan tan A B A B +=⋅,则ABC △的面积为( )A B . C D 12.矩形ABCD 中,22BC AB ==,N 为边BC 的中点,将ABN △沿AN 翻折成1B AN △(1B ∉平面ABCD ),M 为线段1B D 的中点,则在ABN △翻折过程中,下列命题: ①与平面1B AN 垂直的直线必与直线CM 垂直;②线段CM 的长为2; ③异面直线CM 与1NB 所成角的正切值为12; ④当三棱锥1D ANB -的体积最大时,三棱锥1D ANB -外接球表面积是4π.正确的个数为( )A .1个B .2个C .3个D .4个二、填空题13.直线10x ++=的倾斜角为________.14.在ABC △中,若5b =,4B π=,cos A =,则a =________. 15.如图,在ABC △中,D 是BC 的中点,E ,F 是AD 上的两个三等分点5BA CA ⋅=,2BF CF ⋅=-,则BE CE ⋅的值是________.16.如图,正方体1111ABCD A B C D -P 在对角线1BD 上,过点P 作垂直于1BD 的平面,记这样得到的截面多边形含三角形的面积为y ,设BP x =,则当15,22x ⎡⎤∈⎢⎥⎣⎦时,函数()y f x =的值域为________.三、解答题17.已知两直线1l :270x y -+=,2l :10x y +-=,(,)A m n 是1l 和2l 的交点.(1)求过点A 且垂直于直线1l 的直线3l 的方程.(2)求过点A 且平行于直线l :2310x y --=的直线4l 的方程.18.设等差数列{}n a 的前n 项和为n S ,若981S =,3514a a +=(1)求数列{}n a 的通项公式;(2)设11n n n b a a +=,求{}n b 的前n 项和为n T .19.如图,在直三棱柱111ABC A B C -中,D ,E 分别为AB ,BC 的中点,点F 在侧棱1B B 上,且11B D A F ⊥,1111AC A B ⊥.求证:(1)直线//DE 平面11AC F ;(2)直线1B D ⊥平面11AC F .20.ABC △的内角A ,B ,C 的对边分别为a ,b ,c ,已知:2sin 6c a b C π⎛⎫-=-⎪⎝⎭. (1)求B ∠;(2)若ABC △ABC △的周长的最小值.21.如图,边长为2的正方形ABCD 所在的平面与半圆弧CD 所在平面垂直,M 是CD 上异于C ,D 的点.(1)证明:平面AMD ⊥平面BMC ;(2)(理科做)当三棱锥M ABC -体积最大时,求面MAB 与面MCD 所成二面角的正弦值.(文科做)在线段AM 上是否存在点P ,使得//MC 平面PBD ,说明理由.22.已知等差数列{}n a 中,前n 项和为n S ,11a =,{}n b 为等比数列,且各项均为正数,11b =,且满足227b S +=,3322b S +=.(1)求n a 与n b ;(2)记12n n n na cb -⋅=,求{}nc 的前n 项和n T ; (3)若不等式1(1)2n n n n m T --⋅-<对一切*n N ∈恒成立,求实数m 的取值范围.参考答案一、选择题:1-5BDDBA6-10BCADC 11-12AC二、填空题: 13.56π 14. 15.5816.84⎡⎢⎣⎦17.(1)27010x y x y -+=⎧⎨+-=⎩解得(2,3)A -12l k =∴312l k =-∴3l :13(2)2y x -=-+整理得:240x y +-=(2)令4l :230x y m -+=4l 过(2,3)A -,代入得:13m =∴4l :23130x y -+=18.令公差为d(1)91989936812S a d a d ⨯=+=+=①()354122314a a a a d +==+=②由①、②解得:112a d =⎧⎨=⎩ ∴1(1)12221n a a n d n n =+-=+-=-(2)111(21)(21)n n n b a a n n +==-+11122121n n ⎡⎤=⋅-⎢⎥-+⎣⎦ ∴111111123352121n T n n ⎡⎤=-+-++-⎢⎥-+⎣⎦1222121n n n n =⨯=++ 19.(1)//DE AC ,11//DE A CDE ⊄平面11AC F ,11A C ⊂平面11AC F∴//DE 平面11AC F(2)∵1111AC A B ⊥,111AC AA ⊥,1111A B AA A ⋂= ∴11A C ⊥平面11A ABB∴111AC B D ⊥11A F B D ⊥,1111AC A F A =⋂∴1B D ⊥平面11AC F20.(1)2sin 6c a b C π⎛⎫-=- ⎪⎝⎭ 2sin cos cos sin 66b C C ππ⎛⎫=- ⎪⎝⎭sin cos C b C =-由正弦定理得:sin sin sin sin cos C A B C B C -=∵sin sin()sin cos cos sin A B C B C B C =+=+∴①式可化为:sin cos sin sin C B C B C -=∵(0,)C π∈∴sin 0C ≠cos 1B B += 即1sin 62B π⎛⎫+= ⎪⎝⎭,(0,)B π∈ ∴66B ππ+=或56π∴0B =(舍)或23π(2)11sin 22S ac B ac ===∴4ac =∴4a c +≥=22222cos 312b a c ac B a c ac ac =+-=++≥=∴b ≥a c =等号成立∴4l a b c =++≥+21.(1)平面CMD ⊥平面ABCD平面MD ⋂平面ABCD CD =,BC CD ⊥∴BC ⊥平面CMD ,∴BC DM ⊥∵CD 为直径∴CM DM ⊥,BC CM C ⋂=∴DM ⊥平面CMB , DM ⊂ 平面AMD∴平面AMD ⊥平面CMB(2)(理)∵ABC S △为定值∴当高M 到ABC △的距离最大时,三棱锥M ABC -体积最大 即M 为ODM 中点设平面ADMN ⋂ 平面MCD l =//AB CD ,CD ⊂ 平面CMD ,AB ⊄平面CMD ∴//AB 平面CMD ∴////AB l cd过C 作CE l ⊥于E .由(1)知,BC l ⊥l CE E ⋂=∴l ⊥平面BCE ∴l BE ⊥∴BEC ∠为平面MAB 与平面MCD 所成的二面角的平面角∴sin BEC ∠== (文)存在.当P 为AM 中点时,//MC 平面PBD 证明如下:连AC 、BD ,0AC BD ⋂=∵ABCD 为矩形∴O 为AC 中点连OP ,P 为AM 中点,∴//MC OP∵MC ⊄ 平面PBD ,OP ⊂ 平面PBD∴//MC 平面PBD22.(1)令{}n a 的公差为d ,等比数列{}n b 的公比为q 222337117221(1)(12)22b S q d b S q d d +=⎧+++=⎧⇒⎨⎨+=+++++=⎩⎩ 解得:41q d =⎧⎨=⎩,∴14n n n a n b -=⎧⎨=⎩ (2)111242n n n n n n C ---⋅== ∴01211232222n n n T -=++++① ∴123112322222n n n T =++++②①-②,得011111122222n n n n T -=+++- 11121212n n n ⎛⎫- ⎪⎝⎭=-⋅-()1222n n ⎛⎫=-+⋅ ⎪⎝⎭ ∴()11422n n T n -⎛⎫=-+⋅ ⎪⎝⎭(3)原不等式可化为:()()11114222n n n n m n --⎛⎫-⋅-++⋅< ⎪⎝⎭ 即()12142n n m --⋅<- 当n 为奇数时,422m -<-=∴2m >- 当n 为偶数时,413m <-=即3m < 综上,m 的取值范围为(-2,3)。
2019-2020学年黑龙江省大庆一中高一下学期期末数学试卷 (解析版)

2019-2020学年黑龙江省大庆一中高一第二学期期末数学试卷一、选择题(共12小题).1.圆(x+1)2+y2=4的圆心坐标和半径分别是()A.(1,0),2B.(﹣1,0),2C.(1,0),4D.(﹣1,0),4 2.等比数列{a n}中,a2=2,a5=,则公比q=()A.﹣B.﹣2C.2D.3.已知向量=(m,1),=(1,﹣2),若,则m=()A.﹣B.C.﹣2D.24.若x>0,y>0,且=1,则x+y的最小值为()A.6B.12C.16D.245.已知直线l1:mx+(m﹣3)y+1=0,直线l2:(m+1)x+my﹣1=0为,若l1⊥l2,则()A.m=0或m=1B.m=1C.m=﹣D.m=0或m=﹣6.设l为直线,α,β是两个不同的平面,下列命题中正确的是()A.若l∥α,l∥β,则α∥βB.若l⊥α,l⊥β,则α∥βC.若l⊥α,l∥β,则α∥βD.若α⊥β,l∥α,则l⊥β7.若变量x,y满足约束条件,则z=2x+y的最大值为()A.1B.2C.3D.48.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.60πD.68π9.已知等差数列{a n}的前n项和为S n,若a7+a8>0,a7+a9<0,则S n取最大值时n的值是()A.4B.5C.6D.710.在空间四边形ABCD中,已知AD=2,BC=2,E,F分别是AB,CD的中点,EF =,则异面直线AD与BC所成角的大小为()A.B.C.D.11.已知△ABC中,a,b,c分别为角A,B,C所对的边,且a=3,b+c=5,tan A+tan B+=tan A•tan B,则△ABC的面积为()A.B.3C.D.12.矩形ABCD中,BC=2AB=2,N为边BC的中点,将△ABN沿AN翻折成△B1AN(B1∉平面ABCD),M为线段B1D的中点,则在△ABN翻折过程中,下列命题:①与平面B1AN垂直的直线必与直线CM垂直;②线段CM的长为;③异面直线CM与NB1所成角的正切值为;④当三棱锥D﹣ANB1的体积最大时,三棱锥D﹣ANB1外接球表面积是4π.正确的个数为()A.1个B.2个C.3个D.4个二、填空题(共4小题,共20.0分)13.直线x+y+1=0的倾斜角的大小为.14.在△ABC中,若b=5,B=,cos A=,则a=.15.如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,•=5,•=﹣2,则•的值是.16.如图,正方体ABCD﹣A1B1C1D1的棱长为,动点P在对角线BD1上,过点P作垂直于BD1的平面,记这样得到的截面多边形(含三角形)的面积为y,设BP=x,则当x∈时,函数y=f(x)的值域为.三、解答题(共6小题,第17题10分,其余每题12分,计60分)17.已知两直线l1:2x﹣y+7=0,l2:x+y﹣1=0,A(m,n)是l1和l2的交点,(1)求m,n的值;(2)求过点A且垂直于直线l1的直线l3的方程;(3)求过点A且平行于直线l:2x﹣3y﹣1=0的直线l4的方程.18.设等差数列{a n}的前n项和为S n,若S9=81,a3+a5=14.(1)求数列{a n}的通项公式;(2)设b n=,求{b n}的前n项和为T n.19.如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B 上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F:(2)直线B1D⊥平面A1C1F.20.△ABC的内角A,B,C的对边分别为a,b,c,已知:c﹣a=2b sin(C﹣).(1)求∠B;(2)若△ABC面积为,求△ABC的周长的最小值.21.如图,边长为2的正方形ABCD所在的平面与半圆弧所在平面垂直,M是上异于C,D的点.(1)证明:平面AMD⊥平面BMC:(2)(理科做)当三棱锥M﹣ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.(3)(文科做)在线段AM上是否存在点P,使得MC∥平面PBD,说明理由.22.已知等差数列{a n}中,前n项和为S n,a1=1,{b n}为等比数列且各项均为正数,b1=1,且满足:b2+S2=7,b3+S3=22.(Ⅰ)求a n与b n;(Ⅱ)记c n=,求{c n}的前n项和T n;(Ⅲ)若不等式(﹣1)n•m﹣T n<对一切n∈N*恒成立,求实数m的取值范围.参考答案一、选择题(共12小题).1.圆(x+1)2+y2=4的圆心坐标和半径分别是()A.(1,0),2B.(﹣1,0),2C.(1,0),4D.(﹣1,0),4【分析】根据题意,由圆的标准方程分析可得答案.解:根据题意,所给圆的标准方程为(x+1)2+y2=4,其圆心为(﹣1,6),半径r=2;故选:B.2.等比数列{a n}中,a2=2,a5=,则公比q=()A.﹣B.﹣2C.2D.【分析】由已知条件利用等比数列的通项公式能求出公比.解:∵等比数列{a n}中,a2=2,a8=,∴,∴公比q=.故选:D.3.已知向量=(m,1),=(1,﹣2),若,则m=()A.﹣B.C.﹣2D.2【分析】由题意利用两个向量垂直的性质,求出m的值.解:∵向量=(m,1),=(1,﹣2),若,∴•=m﹣2=0,故选:D.4.若x>0,y>0,且=1,则x+y的最小值为()A.6B.12C.16D.24【分析】x+y等于x+y乘以+,展开,利用基本不等式;注意等号成立的条件.解:∵+=1,∴x+y=10++=10+6=16故选:C.5.已知直线l1:mx+(m﹣3)y+1=0,直线l2:(m+1)x+my﹣1=0为,若l1⊥l2,则()A.m=0或m=1B.m=1C.m=﹣D.m=0或m=﹣【分析】由l1⊥l2,得m(m+1)+(m﹣3)m=0,由此能求出m的值.解:∵直线l1:mx+(m﹣3)y+1=8,直线l2:(m+1)x+my﹣1=8,l1⊥l2,解得m=0或m=1.故选:A.6.设l为直线,α,β是两个不同的平面,下列命题中正确的是()A.若l∥α,l∥β,则α∥βB.若l⊥α,l⊥β,则α∥βC.若l⊥α,l∥β,则α∥βD.若α⊥β,l∥α,则l⊥β【分析】根据线面平行的几何特征及面面平行的判定方法,可判断A;根据面面平行的判定方法及线面垂直的几何特征,可判断B;根据线面平行的性质定理,线面垂直及面面垂直的判定定理,可判断C;根据面面垂直及线面平行的几何特征,可判断D.解:若l∥α,l∥β,则平面α,β可能相交,此时交线与l平行,故A错误;若l⊥α,l⊥β,根据垂直于同一直线的两个平面平行,可得B正确;若α⊥β,l∥α,则l与β可能相交,可能平行,也可能线在面内,故D错误;故选:B.7.若变量x,y满足约束条件,则z=2x+y的最大值为()A.1B.2C.3D.4【分析】先根据约束条件画出可行域,设z=2x+y,再利用z的几何意义求最值,只需求出直线z=2x+y过可行域内的点B时,从而得到m值即可.解:作出可行域,作出目标函数线,可得直线与y=x与3x+2y=5的交点为最优解点,故选:C.8.如图,某几何体的三视图是三个半径相等的圆及每个圆中两条互相垂直的半径.若该几何体的体积是,则它的表面积是()A.17πB.18πC.60πD.68π【分析】由已知中的三视图,可得该几何体是球,根据体积求出半径R,进而可得表面积.解:由已知中的三视图,可得该几何体是球,设其半径为R,则×==,故其表面积S=×4πR2+=68π,故选:D.9.已知等差数列{a n}的前n项和为S n,若a7+a8>0,a7+a9<0,则S n取最大值时n的值是()A.4B.5C.6D.7【分析】由等差数列{a n}中,其前n项和为S n,且a7+a8>0,a7+a9<0,推导出a1>0,d<0,且a7>0,a8<0;由此能求出当S n取最大值时,n的值.解:∵等差数列{a n}中,其前n项和为S n,且a7+a8>0,a7+a9<3,∴2a1+13d>0且7a1+14d<0,当S n取最大值时,n=7.故选:D.10.在空间四边形ABCD中,已知AD=2,BC=2,E,F分别是AB,CD的中点,EF =,则异面直线AD与BC所成角的大小为()A.B.C.D.【分析】取BD中点O,连结EO、FO、EF,则OE∥AD,OF∥BC,从而∠EOF是异面直线AD与BC所成角(或所成角的补角),利用余弦定理能求出异面直线AD与BC 所成角.解:取BD中点O,连结EO、FO、EF,∵AD=2,BC=2,E,F分别是AB,CD的中点,EF=,∴∠EOF是异面直线AD与BC所成角(或所成角的补角),∴cos∠EOF===﹣,∴异面直线AD与BC所成角为:π﹣∠EOF=.故选:C.11.已知△ABC中,a,b,c分别为角A,B,C所对的边,且a=3,b+c=5,tan A+tan B+=tan A•tan B,则△ABC的面积为()A.B.3C.D.【分析】由两角和的正切公式求出A+B的值,再求出C的值,利用余弦定理求出b的值,即可计算△ABC的面积.解:△ABC中,tan A+tan B+=tan A•tan B,所以tan A+tan B=﹣(1﹣tan A tan B),又A+B∈(0,π),所以A+B=,由余弦定理得c2=a2+b2﹣5ab cos C=9+b2﹣2×,又b+c=5,…②所以△ABC的面积为S△ABC=ab sin C=×3××=.故选:A.12.矩形ABCD中,BC=2AB=2,N为边BC的中点,将△ABN沿AN翻折成△B1AN(B1∉平面ABCD),M为线段B1D的中点,则在△ABN翻折过程中,下列命题:①与平面B1AN垂直的直线必与直线CM垂直;②线段CM的长为;③异面直线CM与NB1所成角的正切值为;④当三棱锥D﹣ANB1的体积最大时,三棱锥D﹣ANB1外接球表面积是4π.正确的个数为()A.1个B.2个C.3个D.4个【分析】取AB1的中点为E,AD的中点为F,连接EN,EM,FN,B1F,推出CM∥平面AB1N判断①;求解距离判断②;求出异面直线CM与NB1的所成角为∠ENB1的正切函数值判断③;求出三棱锥D﹣ANB1的体积最大时三棱锥D﹣ANB1外接球的球心,进一步求得半径,得外接球的表面积判断④.解:如图,取AB1的中点为E,AD的中点为F,连接EN,EM,FN,B1F,得EM∥AD∥NC,EM=AD=NC,则四边形CNEM为平行四边形,∴直线CM∥平面AB1N,故①正确;∵CM∥EN,∴异面直线CM与NB1的所成角为∠ENB2,tan,故③正确;AB1=1,,∴∠AB2D=90°,同理∠AND=90°,∴正确的命题是①③④,故选:C.二、填空题(本大题共4小题,共20.0分)13.直线x+y+1=0的倾斜角的大小为.【分析】化直线的一般式方程为斜截式,求出直线的斜率,由倾斜角的正切值等于斜率求倾斜角.解:由x+y+1=0,得,设其倾斜角为θ(0≤θ<π),∴θ=.故答案为:.14.在△ABC中,若b=5,B=,cos A=,则a=2.【分析】由已知利用同角三角函数基本关系式可求sin A的值,进而根据正弦定理即可求解a的值.解:∵cos A=,∴sin A==,∴由正弦定理,可得a===2.故答案为:2.15.如图,在△ABC中,D是BC的中点,E,F是AD上的两个三等分点,•=5,•=﹣2,则•的值是.【分析】把所用向量都用表示,结合已知求出的值,则的值可求.解:因为,,于是.故答案为:.16.如图,正方体ABCD﹣A1B1C1D1的棱长为,动点P在对角线BD1上,过点P作垂直于BD1的平面,记这样得到的截面多边形(含三角形)的面积为y,设BP=x,则当x∈时,函数y=f(x)的值域为[,].【分析】根据对称性可得:当x=或时,三角形的面积最小,当x=,即P在BD1中点时,截面为正六边形的面积最大,分别求得最值即可.解:如图:∵正方体ABCD﹣A1B1C1D1的棱长为,∵x∈,根据对称性可得:当x=或时,三角形的面积最小,∴t=,∴y min=×=.此时正六边形的边长为=,故截面面积为6××=.故答案为:[,].三、解答题(本大题共6小题,第17题10分,其余每题12分,计60分)17.已知两直线l1:2x﹣y+7=0,l2:x+y﹣1=0,A(m,n)是l1和l2的交点,(1)求m,n的值;(2)求过点A且垂直于直线l1的直线l3的方程;(3)求过点A且平行于直线l:2x﹣3y﹣1=0的直线l4的方程.【分析】(1)把两直线的方程联立方程组,求得此方程组的解,即可得到m,n的值.(2)由(1)可得A的坐标,再根据两直线垂直,斜率之积等于﹣1求得直线l3的斜率,用点斜式求得直线l3的方程.(3)根据两直线平行,斜率相等,求得直线l4的斜率,用点斜式求得直线l4的方程.解:(1)因为A(m,n)是l1和l2的交点,所以,…解得.…因为,l3⊥l1,所以,…(3)因为l4∥l,所以,…由点斜式得,,即2x﹣3y+13=0.…18.设等差数列{a n}的前n项和为S n,若S9=81,a3+a5=14.(1)求数列{a n}的通项公式;(2)设b n=,求{b n}的前n项和为T n.【分析】(1)直接利用等差数列的性质的应用求出数列的通项公式.(2)利用裂项相消法的应用求出数列的和.解:(1)设首项为a1,公差为d的等差数列{a n}的前n项和为S n,若S9=81,a3+a5=14,所以,解得,(2)由于a n=2n﹣2,所以=.19.如图,在直三棱柱ABC﹣A1B1C1中,D,E分别为AB,BC的中点,点F在侧棱B1B 上,且B1D⊥A1F,A1C1⊥A1B1.求证:(1)直线DE∥平面A1C1F:(2)直线B1D⊥平面A1C1F.【分析】(1)通过证明DE∥AC,进而DE∥A1C1,据此可得直线DE∥平面A1C1F1;(2)证明B1D⊥A1C1,利用A1F⊥B1D,A1F∩A1C1=A1,即可证明B1D⊥平面A1C1F.解:(1)∵D,E分别为AB,BC的中点,∴DE为△ABC的中位线,∵ABC﹣A1B1C1为棱柱,∴DE∥A2C1,∴DE∥平面A1C1F;∴B1D⊥A1C6,∴B1D⊥平面A1C1F.20.△ABC的内角A,B,C的对边分别为a,b,c,已知:c﹣a=2b sin(C﹣).(1)求∠B;(2)若△ABC面积为,求△ABC的周长的最小值.【分析】(1)由正弦定理,三角函数恒等变换的应用化简已知等式,结合sin C≠0,可得sin(B+)=,结合范围B+∈(,),可得B+=,进而解得B的值.(2)由已知利用三角形的面积公式可求ac=4,利用余弦定理,基本不等式,即可计算得解△ABC周长的最小值.解:(1)∵c﹣a=2b sin(C﹣)=2b(sin C﹣cos C)=b sin C﹣b cos C,∴由正弦定理可得sin C﹣sin A=sin B sin C﹣sin B cos C,∴sin C﹣sin C cos B=sin B sin C,∴1﹣cos B=sin B,可得sin(B+)=,∴B+=,可得B=.∴△ABC的面积为=ac sin B=ac,解得:ac=4,当且仅当a=c=6时等号成立,此时△ABC周长取最小值为4+2.21.如图,边长为2的正方形ABCD所在的平面与半圆弧所在平面垂直,M是上异于C,D的点.(1)证明:平面AMD⊥平面BMC:(2)(理科做)当三棱锥M﹣ABC体积最大时,求面MAB与面MCD所成二面角的正弦值.(3)(文科做)在线段AM上是否存在点P,使得MC∥平面PBD,说明理由.【分析】(1)推导出BC⊥平面CMD,从而BC⊥DM,推导出DM⊥CM,从而DM⊥平面BMC,由此能证明平面AMD⊥平面BMC.(2)(理科做)当三棱锥M﹣ABC体积最大时,M为CD中点,以D为原点,DA为x 轴,DC为y轴,过D作平面ABCD的垂线为z轴,建立空间直角坐标系,利用向量法能求出面MAB与面MCD所成二面角的正弦值.(3)(文科做)当P为AM中点时,连结AC,BD,交于点O,则O是AC的中点,连结OP,推导出MC∥OP,从而MC∥平面PBD.解:(1)证明:由题设知,平面CMD⊥平面ABCD,交线为CD,∵BC⊥CD,BC⊂平面ABCD,∴BC⊥平面CMD,∵M为CD上异于C,D的点,且DC为直径,∴DM⊥CM,∵DM⊂平面AMD,∴平面AMD⊥平面BMC.以D为原点,DA为x轴,DC为y轴,过D作平面ABCD的垂线为z轴,建立空间直角坐标系,=(﹣2,1,1),=(0,2,0),=(2,0,0),则,取x=1,得=(1,5,2),∴cos<>==,∴面MAB与面MCD所成二面角的正弦值为.证明如下:∵ABCD是矩形,∴O是AC的中点,连结OP,∵MC⊄平面PBD,OP⊂平面PBD,∴MC∥平面PBD.22.已知等差数列{a n}中,前n项和为S n,a1=1,{b n}为等比数列且各项均为正数,b1=1,且满足:b2+S2=7,b3+S3=22.(Ⅰ)求a n与b n;(Ⅱ)记c n=,求{c n}的前n项和T n;(Ⅲ)若不等式(﹣1)n•m﹣T n<对一切n∈N*恒成立,求实数m的取值范围.【分析】(I)设等差数列{a n}的公差为d,等比数列{b n}的公比为q>0,由a1=1,b1=1,且满足:b2+S2=7,b3+S3=22.可得q+2+d=7,q2+3+3d=22,联立解出即可得出.(Ⅱ)c n==,利用“错位相减法”与等比数列的求和公式即可得出.(Ⅲ)不等式(﹣1)n•m﹣T n<,即(﹣1)n•m﹣4+(2+n)<,化为:(﹣1)n•m<4﹣.对n分类讨论,利用数列的单调性即可得出.解:(I)设等差数列{a n}的公差为d,等比数列{b n}的公比为q>0,∵a1=1,b6=1,且满足:b2+S2=7,b3+S4=22.∴a n=1+(n﹣1)=n,b n=4n﹣4.∴{c n}的前n项和T n=1++3×+…+,∴=1+++…+﹣n=﹣=2﹣(2+n),(Ⅲ)不等式(﹣1)n•m﹣T n<,即(﹣1)n•m﹣4+(2+n)<,当n为偶数时,m<4﹣=.∵(﹣1)n•m﹣T n<对一切n∈N*恒成立,∴实数m的取值范围是.。
黑龙江省大庆市第四中学2024_2025学年高一语文下学期第一次月考试题

D.因为安史之乱给唐朝带来沉重打击,所以中唐的士人将自己的治世志向以儒者的姿态写入唐诗。
(二)好用类文本阅读(本题共3小题,10分)
阅读下面的文字,完成7~9题。
材料一:
网络红人李子柒的美食视频在YouTube上走红。三月桃花开,她采来酿成桃花酒;五月枇杷熟,她摘来制成枇杷酥;还有养蚕、缫丝、刺绣等,无不具有显明的中华传统文化风味,加之低沉悠扬的传统曲风,一种诗意的山居生活情境呼之欲出。这让她拥有了几百万来自不同国家和地区的粉丝,收获两千多万的点击率。
黑龙江省大庆市第四中学2024-2025学年高一语文下学期第一次月考试题
考试时间:150分钟 分值:150分
本试卷分为第Ⅰ卷(阅读题)和第Ⅱ卷(表达题)两部分
第Ⅰ卷(阅读题)
一、现代文阅读(36分)
(一)论述类文本阅读(本题共6小题,18分)
阅读下面的文字,完成1〜3题。
所谓“元典精神”,是指一个民族的“文化元典”所集中体现的原创性精神。这种典籍因其首创性及覆盖面的广袤性、思索的深邃性,而在该民族的历史进程中成为生活的指针。印度的《华陀经》、波斯的《古圣经》,柏拉图、亚里斯多德等先哲的论著,犹太及基督教的《圣经》、伊斯兰教的《可兰经》,都被相关民族视为“圣典”或“元典”。在中华文化系统中,堪称元典的是“六经”,与之相关的《论语》《孟子》《老子》等典籍也具有“元典”性质。
有人认为这样的传播过于肤浅简洁、深度不够,也有人认为这样的传播过于偏向呈现中国的乡土生活,缺乏对中国现实更为丰富的表现。这两种说法对文化传播的理解都过于狭隘。首先,李子柒的视频无疑是大众文化的一部分,让外界看到了中国年轻人生活方式中别有意趣的一面。这种大众文化传播对于增进世界对中国的理解,破除刻板印象有主动意义。其次,李子柒的视频以中国传统乡村生活及其独特的物产为中心,通过生动丰富、具有现场感的介绍,让外界对中国人的生活和文化有了详细可感、生动鲜活的认知,自然而然地跨越文化障碍,也让我们切实感受到一种在新媒体平台上“润物细无声”的文化传播所具有的正面效果。另外,文化传播还要了解受众需求。传播往往不能只考虑“我有什么”,还要考虑“他对什么感爱好”。文化传播既要以我为主,也要对受众有深化理解。假如只是把“我的内容”做单向传播,往往不会产生良好效果。(摘编自《文化传播须要更多李子柒》,有改动)
黑龙江省大庆铁人中学2019~2020学年度高一第1学期期末考试数学试题参考答案

铁人中学2019级高一学年第一学期 期末考试数学试题答案一.选择题(共60分):BCBCA BCBAC DD 二.填空题(共20分)13.5 14.(,5)-∞- 15.31- 16.2π三、解答题 (共70分) 17.(1)解:原式11sincostan1063422πππ=+-=+-= (2)解:原式()1lg92lg 211lg 2lg 2lg 1091lg 0.6log 100.6+-==+⨯ ()2lg 29lg362lg 6lg 6⨯=== 18.{}[][][]1(1).A 013......(1);A ,1,4,3,1,3.....x x x x a b x a b a ⎧+⎫=≤=-≤<=-⎨⎬-⎩⎭∴∈-Q U 分由数形结合知:满足的条件:b=4...(2分),(4分){}[]{}2(2).B (1)20(1)(2)0.21.....(6)21,313;....2121,3,2321,335,3 5 (1121)x x m x m x x x m A B Am B A m m m m m m B m m m m m m =--+-≤=---≤=-≥-⎧∴⊆∴-<<≤<⎨-<⎩-==-<⎧->><<∴<<⎨->⎩Q U 分分情况讨论:若即时得(8分)若即中只有一个元素1符合题意;........(9分)若即时得③(①②{}5......................12m m m ≤<分)综上的取值范围为:1(分)19.(1)2331m m -+=,即2320m m -+=,则()()120m m --=,解得1m =或2m =, 当1m =时,()311122xf x x ---==,当2m =时,()2112322xx f x --==,∵()f x 在()0,∞+上为增函数,∴()12f x x=(2)由(1)得)(x f 定义域为[)∞+,0且()f x 在()0,∞+上为增函数 ⎪⎩⎪⎨⎧-<+≥-≥+∴aa a a 23102301,解得:321<≤-a ,所以a 的取值范围为:⎪⎭⎫⎢⎣⎡-32,120.(1)∵f (x )=2sin (2x 6π-)+a , ∴f (x )的最小正周期T 22π==π. 令解得,,62Z k k x ∈=-ππZ k k x ∈+=,212ππZ k a k x f ∈+∴),,212)(ππ的对称中心为:((2)当x ∈[0,2π]时,2x 6π-∈[6π-,56π], 故当2x 66ππ-=-时,函数f (x )取得最小值,即sin (6π-)12=-,∴f (x )取得最小值为﹣1+a =﹣2, ∴a =﹣1.21.(1)∵)(x f 相邻两条对称轴之间的距离为2π∴f (x )的最小正周期T =π.∴2=ω ∵直线x =是函数y =f (x )的图象的一条对称轴, ∴sin (2×+φ)=±1.∴+φ=k π+,k ∈Z .∵﹣π<φ<0,∴φ=﹣. (2)由y =sin知x 0πy﹣1 0 1 0故函数y =f (x )在区间[0,π]上的图象如图.(3)由已知得x x g 4cos )(-= 令Z k k x k ∈+≤≤+,2242ππππ, ∴函数)(x g y =的单调减区间为⎥⎦⎤⎢⎣⎡++22,42ππππk k ,k ∈Z . 22.(1)令0x y ==,则()()020f f =,即有()00f =,再令y x =-,得()()()00f f x f x =+-=,则()()f x f x -=-, 故()f x 为奇函数;(2)任取12x x <,则210x x ->.由已知得()210f x x -<,则()()()()()121212f x f x f x f x f x x -=+-=-()210f x x -->=, ∴()()12f x f x >,∴()f x 在R 上是减函数.由于()12f =-,则()()2214f f ==-,()()()3126f f f =+=-,()()336f f -=-=.由()f x 在R 上是减函数,得到当[]3,3x ∈-时,()f x 的最大值为()36f -=,最小值为()36f =-; (3)不等式()()()()221122f bx f x f b x f b ->-,即为()()()()2222f bx f x f b x f b ->-. 即()()()()2222f bxf x f b x f b ->-,即有()()2222f bx x f b x b ->-,由于()f x 在R 上是减函数,则2222bx x b x b -<-,即为()22220bx b x b -++<,即有()()20bx x b --<, 当0b =时,得解集为{}|0x x >; 当0b >时,即有()20x b x b ⎛⎫--< ⎪⎝⎭, ①02b <<,2b b >,此时解集为2|x b x b ⎧⎫<<⎨⎬⎩⎭,②当2b >,2b b <,此时解集为2|x x b b ⎧⎫<<⎨⎬⎩⎭, 当0b <时,即有()20x b x b ⎛⎫--> ⎪⎝⎭, ①当20b -<<时,2b b <,此时解集为2|x x x b b ⎧⎫<>⎨⎬⎩⎭或,②当2b <-,2b b >,此时解集为2|x x x b b ⎧⎫><⎨⎬⎩⎭或.。
黑龙江省大庆市第四中学2019-2020学年高一下学期第一次月考数学(理)试题

大庆四中2019~2020学年度第二学期第一次检测高一年级数学(理科)试题 第Ⅰ卷(选择题 共60分)一.选择题(本大题共12小题,每小题5分,满分60分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.下列命题正确的是( ) A. OA OB AB -=B. 0AB BA +=C. 00AB ⋅=D. AB BCAC【★★答案★★】D 【解析】 【分析】根据平面向量加减法法则可判断A 、B 、D 选项的正误,利用平面向量数量积的定义可判断C 选项的正误.【详解】由平面向量加减法法则可得OA OB BA -=,0AB BA +=,AB BC AC ,由平面向量数量积的定义可得00AB ⋅=. 所以,A 、B 、C 选项错误,D 选项正确. 故选:D.【点睛】本题考查平面向量加减法法则的应用,同时也考查了平面向量数量积定义的应用,考查计算能力,属于基础题.2.已知O 为坐标原点,(1,2)OA =,(1,3)AC =-,则点C 的坐标是( ) A. (2,1)-B. (0,5)C. (1,6)-D. (0,1)-【★★答案★★】B 【解析】 【分析】利用向量加法的坐标运算,求得C 的坐标.【详解】依题意()()()1,21,30,5OC OA AC =+=+-=,所以C 的坐标为()0,5. 故选:B【点睛】本小题主要考查向量加法的坐标运算,属于基础题.3.已知,a b 满足1a b ==,,a b 的夹角为120,则a b ⋅= ( )A.12B. 12-D. 1【★★答案★★】B 【解析】 【分析】根据向量的数量积的定义及运算公式,即可求解.【详解】由题意,向量,a b 满足1a b ==,,a b 的夹角为120, 则120cos 1111()22a b a b ⋅==⨯⨯-=⨯-⋅. 故选:B.【点睛】本题主要考查了向量的数量积的定义及运算,其中解答中熟记向量的数量积的概念及运算公式是解答的关键,考查了计算能力.4.已知点()(1,3),2,A B x -,向量(1,2)a =,若//AB a ,则实数x 的值为( ) A. 7B. 8C. 9D. 6【★★答案★★】C 【解析】 【分析】先求得AB ,然后根据向量共线的坐标表示列方程,解方程求得x 的值.【详解】依题意()3,3AB OB OA x =-=-,由于//AB a ,所以()3231x ⨯=-⨯,解得9x =. 故选:C【点睛】本小题主要考查平面向量共线的坐标表示,属于基础题. 5.在ABC ∆中,a ,b ,c 分别为角A ,B ,C 的对边,若2a =,3b =,6A π=,则ABC ∆解的个数是( ) A. 0B. 1C. 2D. 不确定【★★答案★★】C 【解析】【分析】根据余弦定理求出c ,有两个值,由此可得★★答案★★. 【详解】在ABC ∆中,由余弦定理得2222cos a b c bc A =+-,所以2496c c =+-,即250c -+=,解得c =或2c = 所以ABC ∆解的个数是2. 故选:C【点睛】本题考查了利用余弦定理判断三角形的解得个数,属于基础题.6.已知向量()0,5a =,向量()3,1b =-,若a b μ-与a b +垂直,则μ=( ) A. 1-B. 1C.12D.14【★★答案★★】D 【解析】 【分析】根据()0,5a =与()3,1b =-,得出a b μ-与a b +的坐标,再由a b μ-与a b +垂直得到()()0a b a b μ-⋅+=,进而即可得到★★答案★★.【详解】解:因为()0,5a =,()3,1b =-, 所以(0,5)(3,1)(3,51)a b μμμ-=--=-+,(0,5)(3,1)(3,4)a b +=+-=.因为a b μ-与a b +垂直, 所以()()0a b a b μ-⋅+=,所以()()335140μ-⋅++⋅=,解得14μ=. 故选:D.【点睛】本题主要考查平面向量的坐标运算和数量积,考查学生的计算能力,属于基础题.7.在ABC ∆中,若cos cos a cA C b++=,则ABC ∆的形状是( ) A. C 为直角的直角三角形 B. C 为钝角的钝角三角形 C. B 为直角的直角三角形 D. A 为锐角的三角形【★★答案★★】C 【解析】 【分析】利用余弦定理角化边,根据立方和公式变形化简可得222a c b +=,由此可得★★答案★★. 【详解】因为cos cos a cA C b++=, 所以22222222b c a a b c a c bc ab b+-+-++=, 所以222222()()2()a b c a c a b c ac a c +-++-=+, 所以233()()()b a c a c ac a c +-+=+,所以222()()()()b a c a c a ac c ac a c +-+-+=+, 因为0a c +>,所以222()b a ac c ac --+=, 所以222a c b +=, 所以B 为直角. 故选:C【点睛】本题考查了利用余弦定理角化边判断三角形的形状,属于基础题. 8.已知非零向量a b ,满足4b a =,且2)+(a a b ⊥,则a 与b 夹角为( )A. B. C.D.【★★答案★★】C 【解析】 【分析】利用两个向量垂直的性质、两个向量的数量积的定义,求得a 与b 的夹角θ的值.【详解】220a b a ∴⋅+=2()()20++2+20a a a b a a b a b ⊥∴⋅∴⋅,=,=,即220cos a a a b b +〈,〉=.224240b a a a cos a b ∴=,+〈,〉=,12cos ,,,23a b a b π∴〈〉=-∴〈〉=.【点睛】本题主要考查两个向量的数量积的定义,两个向量垂直的性质,属于基础题. 9.在ABC 中,若222cos cos cos 1A B C +->,则ABC 的形状是( ) A. 锐角三角形 B. 钝角三角形C. 直角三角形D. 不能确定【★★答案★★】B 【解析】 【分析】利用三角函数的基本关系式和题设条件,得到222sin sin sin A B C +<,结合正弦定理化简得到222a b c +<,结合三角形的性质,即可求解.【详解】在ABC ∆中,因为222cos cos cos 1A B C +->,可得2221sin 1sin 1sin 1A B C -+--+>,即222sin sin sin A B C +<, 又由正弦定理知2sin sin sin a b c R A B C ===,即sin ,sin ,sin 222a b c A B C R R R===, 可得222a b c +<,所以ABC 钝角三角形.故选:B.【点睛】本题主要考查了利用正弦定理、余弦定理判定三角形的形状,其中解答中合理利用正弦定理的边角互化,以及三角形的性质是解答的关键,着重考查了推理与运算能力. 10.已知O 是平面上一点,,A 、B 、C 是平面上不共线的三个点,点O 满足0AB AC BA BC OA OB AB AC BA BC ⎛⎫⎛⎫ ⎪ ⎪⋅-=⋅-= ⎪ ⎪⎝⎭⎝⎭,则O 点一定是△ABC 的( ) A. 外心B. 内心C. 重心D. 垂心【★★答案★★】B 【解析】【分析】由所给等式利用数量积的定义可得cos<,=cos<,OA AB OA AC >>,推出O 点为BAC ∠的角平分线上的点,同理O 点为ABC ∠的角平分线上的点,即可判断.【详解】0AB AC OA AB AC ⎛⎫ ⎪⋅-= ⎪⎝⎭,=AB AC OA OA AB AC ∴⋅⋅,即cos<,=cos<,AB AC OA OA AB OA OA AC ABAC⋅⋅>⋅⋅>,cos<,=cos<,OA AB OA AC ∴>>,O 点为BAC ∠的角平分线上的点,同理可得O 点为ABC ∠的角平分线上的点,所以O 点为△ABC 角平分线的交点,O 点是一定是△ABC 的内心. 故选:B【点睛】本题考查向量的数量积的定义及运算律、三角形内心的概念,属于中档题. 11.已知1a b ==,且a b ⊥,则2a b+在a b +方向上的投影为( )A.2B.2【★★答案★★】A 【解析】 ∵a b ⊥ ∴0a b ⋅=∴2a b +在a b +方向上的投影为222223(2)()22a a b b a b a b a ba ab b+⋅++⋅+===++⋅+故选A12.在△ABC 中,(cos18,cos 72)AB =,(2sin 27,2sin 63)BC =,则△ABC 的面积为( ) A.4B.2C.2【★★答案★★】B 【解析】 【分析】由于cos72=sin18sin 63=cos27,,化简AB ,BC ,求得模长,根据数量积的坐标公式求得夹角B π-的余弦值,计算可得B ,根据面积公式计算即可求得结果. 【详解】(cos18,cos 72)AB =,(2sin 27,2sin 63)BC =,(cos18,sin18)AB ∴=︒︒,(2sin 27,2cos 27)BC =︒︒,得cos 1AB ==,2cos 2BC ==,由于AB 与BC 的夹角为B π-,2cos18sin 272sin18cos 272cos()sin 45122B π+∴-===⨯,cos ,02B B π∴=-<<,135B =, 因此ABC ∆面积为:1212sin1352⨯⨯⨯=故选:B.【点睛】本题考查向量的坐标表示,数量积公式的灵活应用,考查三角形面积的计算,属于基础题.第Ⅱ卷(非选择题 共90分)二、填空题(本大题共4小题,每小题5分,满分20分.)13.已知向量(2,1)a =,10a b ⋅=,52a b +=,则b =________. 【★★答案★★】5 【解析】 【分析】本题首先可以根据(2,1)a =得出25a =,然后根据52a b +=得出250a b +=,最后通过化简即可得出结果。
黑龙江省大庆市2019-2020学年中考数学第四次调研试卷含解析

黑龙江省大庆市2019-2020学年中考数学第四次调研试卷一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.去年12月24日全国大约有1230000人参加研究生招生考试,1230000这个数用科学记数法表示为( ) A .1.23×106B .1.23×107C .0.123×107D .12.3×1052.在数轴上到原点距离等于3的数是( ) A .3B .﹣3C .3或﹣3D .不知道3.如图在△ABC 中,AC =BC ,过点C 作CD ⊥AB ,垂足为点D ,过D 作DE ∥BC 交AC 于点E ,若BD =6,AE =5,则sin ∠EDC 的值为( )A .35B .725C .45D .24254.我国第一艘航母“辽宁舰”最大排水量为67500吨,用科学记数法表示这个数字是 A .6.75×103吨B .67.5×103吨C .6.75×104吨D .6.75×105吨5.已知点1(,3)A x 、2(,6)B x 都在反比例函数3y x=-的图象上,则下列关系式一定正确的是( ) A .120x x <<B .120x x <<C .210x x <<D .210x x <<6.13-的绝对值是( ) A .3B .3-C .13D .13-7.如图,PA 、PB 是O e 的切线,点D 在»AB 上运动,且不与A ,B 重合,AC 是O e 直径.62P ∠=︒,当//BD AC 时,C ∠的度数是( )A .30°B .31︒C .32︒D .33︒83x +x 的取值范围是( ) A .x≥﹣3B .x≠0C .x≥﹣3且x≠0D .x≥39.有下列四种说法:①半径确定了,圆就确定了;②直径是弦;③弦是直径;④半圆是弧,但弧不一定是半圆.其中,错误的说法有()A.1种B.2种C.3种D.4种10.某校举行“汉字听写比赛”,5个班级代表队的正确答题数如图.这5个正确答题数所组成的一组数据的中位数和众数分别是()A.10,15 B.13,15 C.13,20 D.15,1511.一个不透明的袋子里装着质地、大小都相同的3个红球和2个绿球,随机从中摸出一球,不再放回袋中,充分搅匀后再随机摸出一球.两次都摸到红球的概率是()A.310B.925C.920D.3512.若(x﹣1)0=1成立,则x的取值范围是()A.x=﹣1 B.x=1 C.x≠0D.x≠1二、填空题:(本大题共6个小题,每小题4分,共24分.)13.如图,在正五边形ABCDE中,AC与BE相交于点F,则∠AFE的度数为_____.14.分解因式8x2y﹣2y=_____.15.如图是测量河宽的示意图,AE与BC相交于点D,∠B=∠C=90°,测得BD=120m,DC=60m,EC=50m,求得河宽AB=______m.16.小芸一家计划去某城市旅行,需要做自由行的攻略,父母给她分配了一项任务:借助网络评价选取该城市的一家餐厅用餐.小芸根据家人的喜好,选择了甲、乙、丙三家餐厅,对每家餐厅随机选取了1000条网络评价,统计如下:评价条数 等级餐厅 五星四星三星二星一星合计甲 538 210 96 129 27 1000 乙 460 187 154 169 30 1000 丙4863888113321000(说明:网上对于餐厅的综合评价从高到低,依次为五星、四星、三星、二星和一星.)小芸选择在________(填"甲”、“乙"或“丙”)餐厅用餐,能获得良好用餐体验(即评价不低于四星)的可能性最大. 17.若22m n x y --与423m n x y +是同类项,则3m n -的立方根是 .18.如图,在平面直角坐标系中,四边形OABC 的顶点O 是坐标原点,点A 的坐标(6,0),B 的坐标(0,8),点C 的坐标(﹣25,4),点M ,N 分别为四边形OABC 边上的动点,动点M 从点O 开始,以每秒1个单位长度的速度沿O→A→B 路线向终点B 匀速运动,动点N 从O 点开始,以每秒2个单位长度的速度沿O→C→B→A 路线向终点A 匀速运动,点M ,N 同时从O 点出发,当其中一点到达终点后,另一点也随之停止运动,设动点运动的时间为t 秒(t >0),△OMN 的面积为S .则:AB 的长是_____,BC 的长是_____,当t =3时,S 的值是_____.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(6分)如图,⊙O 是△ABC 的外接圆,AE 平分∠BAC 交⊙O 于点E ,交BC 于点D ,过点E 做直线l ∥BC .(1)判断直线l 与⊙O 的位置关系,并说明理由;(2)若∠ABC 的平分线BF 交AD 于点F ,求证:BE=EF ; (3)在(2)的条件下,若DE=4,DF=3,求AF 的长.20.(6分)我国古代数学著作《增删算法统宗》记载“官兵分布”问题:“一千官军一千布,一官四疋无零数,四军才分布一疋,请问官军多少数.”其大意为:今有1000官兵分1000匹布,1官分4匹,4兵分1匹.问官和兵各几人?21.(6分)如图,△ABC是等腰三角形,AB=AC,点D是AB上一点,过点D作DE⊥BC交BC于点E,交CA延长线于点F.证明:△ADF是等腰三角形;若∠B=60°,BD=4,AD=2,求EC的长,22.(8分)解方程21=122xx x---23.(8分)中华文化,源远流长,在文学方面,《西游记》、《三国演义》、《水浒传》、《红楼梦》是我国古代长篇小说中的典型代表,被称为“四大古典名著”.某中学为了了解学生对四大古典名著的阅读情况,就“四大古典名著你读完了几部”的问题在全校学生中进行了抽样调查,根据调查结果绘制成如图所示的两个不完整的统计图,请结合图中信息解决下列问题:(1)本次调查了名学生,扇形统计图中“1部”所在扇形的圆心角为度,并补全条形统计图;(2)此中学共有1600名学生,通过计算预估其中4部都读完了的学生人数;(3)没有读过四大古典名著的两名学生准备从四大固定名著中各自随机选择一部来阅读,求他们选中同一名著的概率.24.(10分)如图,矩形ABCD绕点C顺时针旋转90°后得到矩形CEFG,连接DG交EF于H,连接AF 交DG于M;(1)求证:AM=FM;(2)若∠AMD=a.求证:DGAF=cosα.25.(10分)工人小王生产甲、乙两种产品,生产产品件数与所用时间之间的关系如表:生产甲产品件数(件)生产乙产品件数(件)所用总时间(分钟)10 10 35030 20 850(1)小王每生产一件甲种产品和每生产一件乙种产品分别需要多少分钟?(2)小王每天工作8个小时,每月工作25天.如果小王四月份生产甲种产品a件(a为正整数).①用含a的代数式表示小王四月份生产乙种产品的件数;②已知每生产一件甲产品可得1.50元,每生产一件乙种产品可得2.80元,若小王四月份的工资不少于1500元,求a的取值范围.26.(12分)某校运动会需购买A、B两种奖品,若购买A种奖品3件和B种奖品2件,共需60元;若购买A种奖品5件和B种奖品3件,共需95元.(1)求A、B两种奖品的单价各是多少元?(2)学校计划购买A、B两种奖品共100件,且A种奖品的数量不大于B种奖品数量的3倍,设购买A 种奖品m件,购买费用为W元,写出W(元)与m(件)之间的函数关系式.请您确定当购买A种奖品多少件时,费用W的值最少.27.(12分)某高科技产品开发公司现有员工50名,所有员工的月工资情况如下表:员工管理人员普通工作人员人员结构总经理部门经理科研人员销售人员高级技工中级技工勤杂工员工数(名) 1 3 2 3 24 1每人月工资(元)21000 8400 2025 2200 1800 1600 950请你根据上述内容,解答下列问题:该公司“高级技工”有名;所有员工月工资的平均数x为2500元,中位数为元,众数为元;小张到这家公司应聘普通工作人员.请你回答右图中小张的问题,并指出用(2)中的哪个数据向小张介绍员工的月工资实际水平更合理些;去掉四个管理人员的工资后,请你计算出其他员工的月平均工资y(结果保留整数),并判断y能否反映该公司员工的月工资实际水平.参考答案一、选择题(本大题共12个小题,每小题4分,共48分.在每小题给出的四个选项中,只有一项是符合题目要求的.) 1.A 【解析】分析:科学记数法的表示形式为10n a ⨯的形式,其中110a ≤<,n 为整数.确定n 的值时,要看把原数变成a 时,小数点移动了多少位,n 的绝对值与小数点移动的位数相同.当原数绝对值>1时,n 是正数;当原数的绝对值<1时,n 是负数.详解:1230000这个数用科学记数法可以表示为61.2310.⨯ 故选A.点睛:考查科学记数法,掌握绝对值大于1的数的表示方法是解题的关键. 2.C 【解析】 【分析】根据数轴上到原点距离等于3的数为绝对值是3的数即可求解. 【详解】绝对值为3的数有3,-3.故答案为C. 【点睛】本题考查数轴上距离的意义,解题的关键是知道数轴上的点到原点的距离为绝对值. 3.A 【解析】 【分析】由等腰三角形三线合一的性质得出AD=DB=6,∠BDC=∠ADC=90°,由AE=5,DE ∥BC 知AC=2AE=10,∠EDC=∠BCD ,再根据正弦函数的概念求解可得. 【详解】∵△ABC 中,AC =BC ,过点C 作CD ⊥AB , ∴AD =DB =6,∠BDC =∠ADC =90°, ∵AE =5,DE ∥BC ,∴AC =2AE =10,∠EDC =∠BCD ,∴sin∠EDC=sin∠BCD=63105 BDBC==,故选:A.【点睛】本题主要考查解直角三角形,解题的关键是熟练掌握等腰三角形三线合一的性质和平行线的性质及直角三角形的性质等知识点.4.C【解析】试题分析:根据科学记数法的定义,科学记数法的表示形式为a×10n,其中1≤|a|<10,n为整数,表示时关键要正确确定a的值以及n的值.在确定n的值时,看该数是大于或等于1还是小于1.当该数大于或等于1时,n为它的整数位数减1;当该数小于1时,-n为它第一个有效数字前0的个数(含小数点前的1个0).67500一共5位,从而67 500=6.75×2.故选C.5.A【解析】分析:根据反比例函数的性质,可得答案.详解:由题意,得k=-3,图象位于第二象限,或第四象限,在每一象限内,y随x的增大而增大,∵3<6,∴x1<x2<0,故选A.点睛:本题考查了反比例函数,利用反比例函数的性质是解题关键.6.C【解析】【分析】根据数轴上某个数与原点的距离叫做这个数的绝对值的定义即可解决.【详解】在数轴上,点13-到原点的距离是13,所以,13-的绝对值是13,故选C.【点睛】错因分析容易题,失分原因:未掌握绝对值的概念. 7.B【解析】 【分析】连接OB ,由切线的性质可得90∠=∠=︒PAO PBO ,由邻补角相等和四边形的内角和可得62∠=∠=︒BOC P ,再由圆周角定理求得D ∠,然后由平行线的性质即可求得C ∠.【详解】 解,连结OB ,∵PA 、PB 是O e 的切线,∴PA OA ⊥,PB OB ⊥,则90∠=∠=︒PAO PBO ,∵四边形APBO 的内角和为360°,即++360∠∠∠+∠=︒PAO PBO P AOB , ∴180∠+∠=︒P AOB ,又∵62P ∠=︒,180∠+∠=︒BOC AOB , ∴62∠=∠=︒BOC P ,∵»»BCBC =, ∴1312∠=∠=︒D BOC , ∵//BD AC , ∴31∠=∠=︒C D , 故选:B . 【点睛】本题主要考查了切线的性质、圆周角定理、平行线的性质和四边形的内角和,解题的关键是灵活运用有关定理和性质来分析解答. 8.C 【解析】 【分析】根据二次根式有意义和分式有意义的条件列出不等式,解不等式即可. 【详解】由题意得,x+3≥0,x≠0,解得x≥−3且x≠0,故选C.【点睛】本题考查分式有意义条件,二次根式有意义的条件,熟练掌握相关知识是解题的关键.9.B【解析】【分析】根据弦的定义、弧的定义、以及确定圆的条件即可解决.【详解】解:圆确定的条件是确定圆心与半径,是假命题,故此说法错误;直径是弦,直径是圆内最长的弦,是真命题,故此说法正确;弦是直径,只有过圆心的弦才是直径,是假命题,故此说法错误;④半圆是弧,但弧不一定是半圆,圆的任意一条直径的两个端点把圆分成两条弧,每一条弧都叫半圆,所以半圆是弧.但比半圆大的弧是优弧,比半圆小的弧是劣弧,不是所有的弧都是半圆,是真命题,故此说法正确.其中错误说法的是①③两个.故选B.【点睛】本题考查弦与直径的区别,弧与半圆的区别,及确定圆的条件,不要将弦与直径、弧与半圆混淆.10.D【解析】【分析】将五个答题数,从小打到排列,5个数中间的就是中位数,出现次数最多的是众数.【详解】将这五个答题数排序为:10,13,15,15,20,由此可得中位数是15,众数是15,故选D.【点睛】本题考查中位数和众数的概念,熟记概念即可快速解答.11.A【解析】【分析】列表或画树状图得出所有等可能的结果,找出两次都为红球的情况数,即可求出所求的概率:【详解】列表如下:∵所有等可能的情况数为20种,其中两次都为红球的情况有6种,∴63P2010==两次红,故选A.12.D【解析】试题解析:由题意可知:x-1≠0,x≠1故选D.二、填空题:(本大题共6个小题,每小题4分,共24分.)13.72°【解析】【分析】首先根据正五边形的性质得到AB=BC=AE,∠ABC=∠BAE=108°,然后利用三角形内角和定理得∠BAC=∠BCA=∠ABE=∠AEB=(180°−108°)÷2=36°,最后利用三角形的外角的性质得到∠AFE=∠BAC+∠ABE=72°.【详解】∵五边形ABCDE为正五边形,∴AB=BC=AE,∠ABC=∠BAE=108°,∴∠BAC=∠BCA=∠ABE=∠AEB=(180°−108°)÷2=36°,∴∠AFE=∠BAC+∠ABE=72°,故答案为72°.【点睛】本题考查的是正多边形和圆,利用数形结合求解是解答此题的关键14.2y(2x+1)(2x﹣1)【解析】【分析】首先提取公因式2y,再利用平方差公式分解因式得出答案.【详解】8x2y-2y=2y(4x2-1)=2y(2x+1)(2x-1).故答案为2y(2x+1)(2x-1).【点睛】此题主要考查了提取公因式法以及公式法分解因式,正确应用公式是解题关键.15.1【解析】【分析】由两角对应相等可得△BAD∽△CED,利用对应边成比例即可得两岸间的大致距离AB的长.【详解】解:∵∠ADB=∠EDC,∠ABC=∠ECD=90°,∴△ABD∽△ECD,∴AB BD EC CD=,即BD EC ABCD⨯=,解得:AB=1205060⨯=1(米).故答案为1.【点睛】本题主要考查了相似三角形的应用,用到的知识点为:两角对应相等的两三角形相似;相似三角形的对应边成比例.16.丙【解析】【分析】不低于四星,即四星与五星的和居多为符合题意的餐厅.【详解】不低于四星,即比较四星和五星的和,丙最多.故答案是:丙.【点睛】考查了可能性的大小和统计表.解题的关键是将问题转化为比较四星和五星的和的多少.17.2.【解析】试题分析:若22m n x y --与423m n x y +是同类项,则:4{22m n m n -=+=,解方程得:2{2m n ==-.∴3m n -=2﹣3×(﹣2)=8.8的立方根是2.故答案为2.考点:2.立方根;2.合并同类项;3.解二元一次方程组;4.综合题.18.10, 1, 1【解析】【分析】作CD ⊥x 轴于D ,CE ⊥OB 于E ,由勾股定理得出AB =10,OC 1,求出BE =OB ﹣OE =4,得出OE =BE ,由线段垂直平分线的性质得出BC =OC =1;当t =3时,N 到达C 点,M 到达OA 的中点,OM =3,ON =OC =1,由三角形面积公式即可得出△OMN 的面积.【详解】解:作CD ⊥x 轴于D ,CE ⊥OB 于E ,如图所示:由题意得:OA =1,OB =8,∵∠AOB =90°,∴AB 10;∵点C 的坐标(﹣4),∴OC =1,OE =4,∴BE =OB ﹣OE =4,∴OE =BE ,∴BC =OC =1;当t =3时,N 到达C 点,M 到达OA 的中点,OM =3,ON =OC =1,∴△OMN 的面积S =12×3×4=1; 故答案为:10,1,1.【点睛】本题考查了勾股定理、坐标与图形性质、线段垂直平分线的性质、三角形面积公式等知识;熟练掌握勾股定理是解题的关键.三、解答题:(本大题共9个小题,共78分,解答应写出文字说明、证明过程或演算步骤.19.(1)直线l与⊙O相切;(2)证明见解析;(3).【解析】试题分析:(1)连接OE、OB、OC.由题意可证明,于是得到∠BOE=∠COE,由等腰三角形三线合一的性质可证明OE⊥BC,于是可证明OE⊥l,故此可证明直线l与⊙O相切;(2)先由角平分线的定义可知∠ABF=∠CBF,然后再证明∠CBE=∠BAF,于是可得到∠EBF=∠EFB,最后依据等角对等边证明BE=EF即可;(3)先求得BE的长,然后证明△BED∽△AEB,由相似三角形的性质可求得AE的长,于是可得到AF 的长.试题解析:(1)直线l与⊙O相切.理由如下:如图1所示:连接OE、OB、OC.∵AE平分∠BAC,∴∠BAE=∠CAE.∴.∴∠BOE=∠COE.又∵OB=OC,∴OE⊥BC.∵l∥BC,∴OE⊥l.∴直线l与⊙O相切.(2)∵BF平分∠ABC,∴∠ABF=∠CBF.又∵∠CBE=∠CAE=∠BAE,∴∠CBE+∠CBF=∠BAE+∠ABF.又∵∠EFB=∠BAE+∠ABF,∴∠EBF=∠EFB.∴BE=EF.(3)由(2)得BE=EF=DE+DF=1.∵∠DBE=∠BAE,∠DEB=∠BEA,∴△BED∽△AEB.∴,即,解得;AE=,∴AF=AE﹣EF=﹣1=.考点:圆的综合题.20.官有200人,兵有800人【解析】【分析】设官有x人,兵有y人,根据1000官兵正好分1000匹布,即可得出关于x,y的二元一次方程组,解之即可得出结论.【详解】解:设官有x人,兵有y人,依题意,得:10001410004x yx y+=⎧⎪⎨+=⎪⎩,解得:200800xy=⎧⎨=⎩.答:官有200人,兵有800人.【点睛】本题主要考查二元一次方程组的应用,根据题意列出二元一次方程组是解题的关键. 21.(1)见解析;(2)EC=1.【解析】【分析】(1)由AB=AC,可知∠B=∠C,再由DE⊥BC,可知∠F+∠C=90°,∠BDE+∠B=90°,然后余角的性质可推出∠F=∠BDE,再根据对顶角相等进行等量代换即可推出∠F=∠FDA,于是得到结论;(2)根据解直角三角形和等边三角形的性质即可得到结论.【详解】(1)∵AB=AC,∴∠B=∠C,∵FE⊥BC,∴∠F+∠C=90°,∠BDE+∠B=90°,∴∠F=∠BDE,而∠BDE=∠FDA,∴∠F=∠FDA,∴AF=AD,∴△ADF是等腰三角形;(2)∵DE⊥BC,∴∠DEB=90°,∵∠B=60°,BD=1,∴BE=12BD=2,∵AB=AC,∴△ABC是等边三角形,∴BC=AB=AD+BD=6,∴EC=BC﹣BE=1.【点睛】本题主要考查等腰三角形的判定与性质、余角的性质、对顶角的性质等知识点,关键根据相关的性质定理,通过等量代换推出∠F=∠FDA,即可推出结论.22.x=-1.【解析】【分析】【详解】解:方程两边同乘x-2,得2x=x-2+1解这个方程,得x= -1检验:x= -1时,x-2≠0∴原方程的解是x= -1首先去掉分母,观察可得最简公分母是(x﹣2),方程两边乘最简公分母,可以把分式方程转化为整式方程求解,然后解一元一次方程,最后检验即可求解23.(1)40、126(2)240人(3)1 4【解析】【分析】(1)用2部的人数10除以2部人数所占的百分比25%即可求出本次调查的学生数,根据扇形圆心角的度数=部分占总体的百分比×360°,即可得到“1部”所在扇形的圆心角;(2)用1600乘以4部所占的百分比即可;(3)根据树状图所得的结果,判断他们选中同一名著的概率.【详解】(1)调查的总人数为:10÷25%=40,∴1部对应的人数为40﹣2﹣10﹣8﹣6=14,则扇形统计图中“1部”所在扇形的圆心角为:1440×360°=126°;故答案为40、126;(2)预估其中4部都读完了的学生有1600×640=240人;(3)将《西游记》、《三国演义》、《水浒传》、《红楼梦》分别记作A,B,C,D,画树状图可得:共有16种等可能的结果,其中选中同一名著的有4种,故P(两人选中同一名著)=416=14.【点睛】本题考查了扇形统计图和条形统计图的综合,用样本估计总体,列表法或树状图法求概率.解答此类题目,要善于发现二者之间的关联点,即两个统计图都知道了哪个量的数据,从而用条形统计图中的具体数量除以扇形统计图中占的百分比,求出样本容量,进而求解其它未知的量.24.(1)见解析;(2)见解析.【解析】【分析】(1)由旋转性质可知:AD=FG,DC=CG,可得∠CGD=45°,可求∠FGH=∠FHG=45°,则HF=FG=AD,所以可证△ADM≌△MHF,结论可得.(2)作FN⊥DG垂足为N,且MF=FG,可得HN=GN,且DM=MH,可证2MN=DG,由第一问可得2MF=AF,由cosα=cos∠FMG=MNMF,代入可证结论成立【详解】(1)由旋转性质可知:CD=CG且∠DCG=90°,∴∠DGC=45°从而∠DGF=45°,∵∠EFG=90°,∴HF=FG=AD又由旋转可知,AD∥EF,∴∠DAM=∠HFM,又∵∠DMA=∠HMF,∴△ADM≌△FHM∴AM=FM(2)作FN⊥DG垂足为N∵△ADM≌△MFH∴DM=MH,AM=MF=12AF∵FH=FG,FN⊥HG∴HN=NG∵DG=DM+HM+HN+NG=2(MH+HN)∴MN=12DG∵cos∠FMG=MN MF∴cos∠AMD=2=2MN DG MF AF∴DG AF=cosα 【点睛】本题考查旋转的性质,矩形的性质,全等三角形的判定,三角函数,关键是构造直角三角形. 25.(1)小王每生产一件甲种产品和每生产一件乙种产品分别需要15分钟、20分钟;(2)①600-34a ;② a≤1.【解析】【分析】(1)设生产一件甲种产品和每生产一件乙种产品分别需要x 分钟、y 分钟,根据图示可得:生产10件甲产品,10件乙产品用时350分钟,生产30件甲产品,20件乙产品,用时850分钟,列方程组求解; (2)①根据生产一件甲种产品和每生产一件乙种产品分别需要的时间关系即可表示出结果;②根据“小王四月份的工资不少于1500元”即可列出不等式.【详解】(1)设生产一件甲种产品需x 分钟,生产一件乙种产品需y 分钟,由题意得: 10103503020850x y x y +=⎧⎨+=⎩, 解这个方程组得:1520x y =⎧⎨=⎩, 答:小王每生产一件甲种产品和每生产一件乙种产品分别需要15分钟、20分钟;(2)①∵生产一件甲种产品需15分钟,生产一件乙种产品需20分钟,∴一小时生产甲产品4件,生产乙产品3件,所以小王四月份生产乙种产品的件数:3(25×8﹣4a )=600-3a 4; ②依题意:1.5a+2.8(600-3a 4)≥1500, 1680﹣0.6a≥1500,解得:a≤1.【点睛】本题考查了二元一次方程组的应用、一元一次不等式的应用,正确理解题意,找准题中的等量关系列出方程组、不等关系列出不等式是解题的关键.26.(1)A 、B 两种奖品的单价各是10元、15元;(2)W (元)与m (件)之间的函数关系式是W=﹣5m+1,当购买A 种奖品75件时,费用W 的值最少.【解析】【分析】(1)设A 种奖品的单价是x 元、B 种奖品的单价是y 元,根据题意可以列出相应的方程组,从而可以求得A 、B 两种奖品的单价各是多少元;(2)根据题意可以得到W (元)与m (件)之间的函数关系式,然后根据A 种奖品的数量不大于B 种奖品数量的3倍,可以求得m 的取值范围,再根据一次函数的性质即可解答本题.【详解】(1)设A 种奖品的单价是x 元、B 种奖品的单价是y 元,根据题意得:32605395x y x y +=⎧⎨+=⎩解得:1015x y =⎧⎨=⎩. 答:A 种奖品的单价是10元、B 种奖品的单价是15元.(2)由题意可得:W=10m+15(100﹣m )=﹣5m+1.∵A 种奖品的数量不大于B 种奖品数量的3倍,∴m≤3(100﹣m ),解得:m≤75∴当m=75时,W 取得最小值,此时W=﹣5×75+1=2.答:W (元)与m (件)之间的函数关系式是W=﹣5m+1,当购买A 种奖品75件时,费用W 的值最少.【点睛】本题考查了一次函数的应用、二元一次方程组的应用、一元一次不等式的应用,解答本题的关键是明确题意,找出所求问题需要的条件,利用一次函数的性质解答.27.(1)16人;(2)工中位数是1700元;众数是1600元;(3)用1700元或1600元来介绍更合理些.(4)y 能反映该公司员工的月工资实际水平.【解析】【分析】(1)用总人数50减去其它部门的人数;(2)根据中位数和众数的定义求解即可;(3)由平均数、众数、中位数的特征可知,平均数易受极端数据的影响,用众数和中位数映该公司员工的月工资实际水平更合适些;(4)去掉极端数据后平均数可以反映该公司员工的月工资实际水平.【详解】(1)该公司“高级技工”的人数=50﹣1﹣3﹣2﹣3﹣24﹣1=16(人);(2)工资数从小到大排列,第25和第26分别是:1600元和1800元,因而中位数是1700元; 在这些数中1600元出现的次数最多,因而众数是1600元;(3)这个经理的介绍不能反映该公司员工的月工资实际水平.用1700元或1600元来介绍更合理些.(4)2500502100084003171346y⨯--⨯=≈(元).y能反映该公司员工的月工资实际水平.。
黑龙江省大庆市第四中学2019-2020学年高一数学下学期第一次月考试题文【含答案】

21.(本小题满分 12 分)
设函数 f x sinx sinx ,其中 0 6 ,已知 f 0
6 2
6
(1)求 ;
(2)将函数 y f x的图像上的各点的横坐标伸长为原来的 2 倍(纵坐标不变),再将得到
一、选择题:(本大题共 12 小题,每小题 5 分,满分 60 分.在每小题给出的四个选项中,
只有一项是符合题目要求的)
1.下列命题正确的是
(
)
A. OA-OB=AB
B. AB BA 0
C. 0 AB=0
D. AB+BC=AC
2.已知 O 是坐标原点, OA (1, 2) , AC (1,3) ,则点 C 的坐标是
(1)
f
0
1,
f
4
1
1 2
b cos 0
c sin
0
1,
1 2
b
cos
2
c sin
2
1
b 1 ,c 1
2
2
(2)f x 1 cos 2x 1 sin 2x 1 2 cos 2x 1
2
2
2
4 2
周期T ,函数f x的图像的两条对称轴之间的最短距离为
, ABC 是
(
)
A.以 AB 为底边的等腰三角形 C.以 AB 为斜边的直角三角形
B. 以 BC 为底边的等腰三角形 D. 以 BC 为斜边的直角三角形
11.已知 是第四象限角, tan 7 ,则 sin 4 等于
(
4
3
)
43 3 A.
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
大庆四中2019~2020学年度第二学期第三次检测高一年级
数学(理科)试题答案选择题
题号123456789101112选项A C B D B D C B B A D C 填空题
13、1014、)
54
,53(),54,53(--15、816、2
3
17、解:(1)函数f (x )=ax 2﹣2(a +1)x +b (a ,b ∈R ),
由不等式f (x )<0的解集为(1,2),得a >0,
且1和2是方程ax 2﹣2(a +1)x +b =0的两根;
则,
解得a =2,b =4;
(2)b =4时,不等式为ax 2﹣2(a +1)x +4>0,
可化为(ax ﹣2)(x ﹣2)>0,则
因为a >0,所以不等式化为(x ﹣)(x ﹣2)>0,
令=2,得a =1,
当a >1时,<2,解不等式得x <或x >2;
当a =1时,不等式为(x ﹣2)2>0,解得x ≠2;
当0<a <1时,>2,解不等式得x <2或x >;
综上:当a>1时,不等式的解集为;
当a=1时,不等式的解集为{x|x≠2};
当0<a<1时,不等式的解集为;
18.证明:(1)连接A1B,交AB1于点O,连接DO,如图所示;
因为A1C∥平面ADB1,平面A1BC∩ADB1=OD,
所以A1C∥OD;
又O为A1B的中点,所以OD是△A1BC的中位线,
所以D是BC的中点;
(2)由(1)知D是BC的中点,且AB=AC,
所以AD⊥BC;
又A1C⊥BC,A1C∥OD,
所以OD⊥BC;
又AD∩OD=D,
所以BC⊥平面ADB1;
又BC⊂平面BCC1B1,
所以平面ADB1⊥平面BCC1B1.
19、解:(1)在△APC中,因为,AP=2,AC•PC=4,
设AC=x,则PC=,由余弦定理可得:22=x2+()2﹣2•cos,可得x =2,
则AC=PC=AP,此时△APC为等边三角形,从而∠APB=.
=AC•BC•sin=,可得BC=5,则BP=3,
(2)由S
△ABC
作AD⊥BC交BC于D,由(1)可知,在等边△APC中,AD=,PD=1,
在Rt△ABD中,AB===,
在△ABP中,由正弦定理可得=,
所以sin∠PAB==.
20、(Ⅰ)证明:取AD的中点P,连接MP,NP,
由N,P分别为BD,AD的中点,得NP∥AB,且NP=AB,
又MC∥AB,且MC=AB,∴MC∥NP且MC=NP,得四边形MCNP为平行四边形,∴CN∥MP,又CN⊄平面DAM,MP⊂平面DAM,
∴CN∥平面DAM;
(Ⅱ)解:由AM=BM=,AB=2,可得AB2=AM2+BM2,得AM⊥BM.
又BM⊥AD,AD∩AM=A,∴BM⊥平面ADM,
∵BM⊂平面ABCM,∴平面ADM⊥平面ABCM.
取AM的中点为E,连接DE,
∵AD=DM=1,AD⊥DM,可得DE=,且DE⊥平面ABCM,
∴=.
取BC的中点F,连接EF,则EF=,EF⊥BC,
∵DE⊥平面ABCM,可得DE⊥EF,DE⊥BC,∴DF=.
由BC⊥平面DEF,得BC⊥DF,
∴.
设点A到平面BCD的距离为d,
则,
解得d=.
21、解:(1)设等差数列{a n}的公差为d,且d>0,前n项和为S n,
由S1=1,可得a1=1,S2=2a1+d=2+d,S3=3a1+3d=3+3d,S4=4a1+6d=4+6d,
又S2,S3﹣1,S4成等比数列,可得S2S4=(S3﹣1)2,即为(2+d)(4+6d)=(3+3d ﹣1)2,
解得d=2(﹣舍去),
则a n=1+2(n﹣1)=2n﹣1,n∈N*;
(2)==(﹣1)n(+),
则数列{b n}的前2n项和T2n=﹣(+)+(+)﹣(+)+…﹣(+)+(+)=﹣+=﹣.
22、解:(1)b n=2n,n∈N*.
(2)因为∁n=|a n|•b n=|2n﹣5|•2n,n=1时,T1=6;n=2时,T2=10,当n≥3时,2n﹣5>0,
T n=10+1•23+3•24+…+(2n﹣7)•2n﹣1+(2n﹣5)•2n,①
2T n=20+1•24+3•25+…+(2n﹣7)•2n+(2n﹣5)•2n+1,②
①﹣②可得﹣T n=﹣10+8+2(24+25+…+2n)﹣(2n﹣5)•2n+1
=﹣2+2•﹣(2n﹣5)•2n+1,化简可得T n=34+(2n﹣5)•2n+1,
所以T n=.。
