材料力学全ppt课件
合集下载
材料力学PPT课件

假设在固体所占有的空间内毫无空隙的充满了物质
假设材料的力学性能在各处都是相同的。 假设变形固体各个方向的力学性能都相同
均匀性假设
各向同性假设
材料力学的基本知识
材料的力学性能
-----指变形固体在力的作用下所表现的力学性能。
构件的承载能力:
强度---构件抵抗破坏的能力 刚度---构件抵抗变形的能力 稳定性---构件保持原有平衡状态的能力
FQ=FQ(x) Mc=M(x)
典型例题-2
简支梁受力偶作用
1.
求支座反力FAY,FBY得: FAY=- FBY =M/l
AC段X截面处剪力FQ=Fay, 3. 同理可求得BC段剪力与AC 段相同,剪力图如左
2.
4.
AC段弯矩方程M1
M1=FAY·=M · /L x x BC段弯矩方程M2
5.
弯曲梁的内力
弯曲梁的概念及其简化 杆件在过杆轴线的纵向平面内,受到力偶或受到 垂直于轴线的横向力作用时,杆的轴线将由直线 变为曲线,杆件的这种以轴线变弯为主要特征的 变形称为弯曲;以弯曲为主要变形的杆简称为梁。 常见梁的力学模型 简支梁
一端为活动铰链支座,另一端为固定铰 链支座 一端或两端伸出支座支外的简支梁
A点:x1 0 M1A 0; C点:x1 a M1C 5 q a 2 6
C点:x 2 a , M 2C 5 q.a 2 6 D点:x 2 2a , M 2D 7 q.a 2 6
D点:x 3 a , M 3D 7 q a 2 M 2 D 6 B点:x 3 0, M 3B q a 2 M
转动
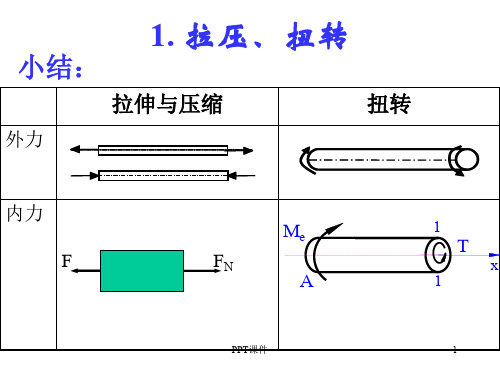
内力:作用面与横截面重 合的一个力偶,称为扭矩T
材料力学 ppt课件
③应力分析:画危险面应力分布图,叠加;
④强度计算:建立危险点的强度条件,进行强度
计算。
PPT课件
20
2、两相互垂直平面内的弯曲
有棱角的截面
max
Mz Wz
My Wy
[ ]
圆截面
max
M
2 z
M
2 y
[ ]
W
3、拉伸(压缩)与弯曲
有棱角的截面
max
FN ,max A
(4)确定最大剪力和最大弯矩
3、弯曲应力与强度条件
(1)弯曲正应力
My
I PPT课件 z
12
M max Wz
yt,max yc,max
Oz y
PPT课件
t,max
Myt,max Iz
c,max
Myc,max Iz
13
(2)梁的正应力强度条件
M max
Wz
M
2 z
M
2 y
T
2
Mr4
M
2 z
M
2 y
0.75T
2
PPT课件
22
5、连接件的强度条件
剪切的强度条件
FS [ ]
AS
挤压强度条件
bs
Fbs Abs
[ bs ]
PPT课件
M z,max Wz
M y,max Wy
[ ]
圆截面
max
FN ,max A PPT课件
M max W
[ ]
21
4、弯曲与扭转
《材料力学第二章》课件

弹性变形与塑性变形的区别
弹性变形是可恢复的,而塑性变形是不可恢复的。
弹性变形能与塑性变形能
弹性变形能
01
物体在弹性变形过程中所吸收的能量,与应力和应变关系呈正
比。
塑性变形能
02
物体在塑性变形过程中所吸收的能量,与应力和应变关系呈非
线性。
弹性变形能与塑性变形能的比较
03
弹性变形能是可逆的,而塑性变形能是不可逆的。
材料力学的重要性
总结词
材料力学是工程设计和科学研究的重要基础,对于保证工程安全、优化产品设 计、降低成本等方面具有重要意义。
详细描述
在工程设计和科学研究中,材料力学提供了对材料行为的深入理解,有助于保 证工程结构的稳定性和安全性,优化产品的设计,降低生产成本,提高经济效 益。
材料力学的基本假设和单位
04
CATALOGUE
变形分析
变形的基本概念
变形
物体在外力作用下,形状 和尺寸发生变化的现象。
弹性变形
当外力去除后,物体能够 恢复原状的变形。
塑性变形
当外力去除后,物体不能 恢复原状的变形。
弹性变形与塑性变形
弹性变形特点
可逆、无残余应变、与外力大小成正比。
塑性变形特点
不可逆、有残余应变、外力达到屈服极限后发生。
建筑结构的优化设计
利用材料力学理论,对建筑结构进行优化设计,降低建筑物的重量 和成本,提高建筑物的性能和寿命。
机械工程中的应用
机械零件的强度和刚度分析
利用材料力学知识,对机械零件的强度和刚度进行分析和计算,确保零件在使用过程中不 会发生断裂或变形。
机械设备的动力学分析
通过材料力学的方法,对机械设备的动力学特性进行分析和计算,确保机械设备在使用过 程中具有良好的稳定性和可靠性。
弹性变形是可恢复的,而塑性变形是不可恢复的。
弹性变形能与塑性变形能
弹性变形能
01
物体在弹性变形过程中所吸收的能量,与应力和应变关系呈正
比。
塑性变形能
02
物体在塑性变形过程中所吸收的能量,与应力和应变关系呈非
线性。
弹性变形能与塑性变形能的比较
03
弹性变形能是可逆的,而塑性变形能是不可逆的。
材料力学的重要性
总结词
材料力学是工程设计和科学研究的重要基础,对于保证工程安全、优化产品设 计、降低成本等方面具有重要意义。
详细描述
在工程设计和科学研究中,材料力学提供了对材料行为的深入理解,有助于保 证工程结构的稳定性和安全性,优化产品的设计,降低生产成本,提高经济效 益。
材料力学的基本假设和单位
04
CATALOGUE
变形分析
变形的基本概念
变形
物体在外力作用下,形状 和尺寸发生变化的现象。
弹性变形
当外力去除后,物体能够 恢复原状的变形。
塑性变形
当外力去除后,物体不能 恢复原状的变形。
弹性变形与塑性变形
弹性变形特点
可逆、无残余应变、与外力大小成正比。
塑性变形特点
不可逆、有残余应变、外力达到屈服极限后发生。
建筑结构的优化设计
利用材料力学理论,对建筑结构进行优化设计,降低建筑物的重量 和成本,提高建筑物的性能和寿命。
机械工程中的应用
机械零件的强度和刚度分析
利用材料力学知识,对机械零件的强度和刚度进行分析和计算,确保零件在使用过程中不 会发生断裂或变形。
机械设备的动力学分析
通过材料力学的方法,对机械设备的动力学特性进行分析和计算,确保机械设备在使用过 程中具有良好的稳定性和可靠性。
材料力学课件PPT

力学性质:在外力作用下材料在变形和破坏方面所 表现出的力学性能
一
试
件
和
实
常
验
温
条
、
件
静
载
材料拉伸时的力学性质
材料拉伸时的力学性质
二 低 碳 钢 的 拉 伸
材料拉伸时的力学性质
二 低碳钢的拉伸(含碳量0.3%以下)
e
b
f 2、屈服阶段bc(失去抵抗变 形的能力)
b
e P
a c s
s — 屈服极限
(二)关于塑性流动的强度理论
1.第三强度理论(最大剪应力理论) 这一理论认为最大剪应力是引起材料塑性流动破坏的主要
因素,即不论材料处于简单还是复杂应力状态,只要构件危险 点处的最大剪应力达到材料在单向拉伸屈服时的极限剪应力就 会发生塑性流动破坏。
这一理论能较好的解释塑性材料出现的塑性流动现象。 在工程中被广泛使用。但此理论忽略了中间生应力 2的影响, 且对三向均匀受拉时,塑性材料也会发生脆性断裂破坏的事 实无法解释。
许吊起的最大荷载P。
CL2TU8
解: N AB
A [ ]
0.0242 4
40 106
18.086 103 N 18.086 kN
P = 30.024 kN
6.5圆轴扭转时的强度计算
圆轴扭转时的强度计算
▪ 最大剪应力:圆截面边缘各点处
max
Tr
Ip
max
Wp T
Wp
Ip r
—
抗扭截面模量
3、强化阶段ce(恢复抵抗变形
的能力)
o
b — 强度极限
4、局部径缩阶段ef
明显的四个阶段
1、弹性阶段ob
材料力学全套ppt课件

___ 不满足上述要求,
不能保证安全工作.
若:不恰当地加大横截面尺寸或
选用优质材料
___ 增加成本,造成浪费
}均 不 可 取
研究构件的强度、刚度和稳定性,还需要了解材料的力学性能。因此在 进行理论分析的基础上,实验研究是完成材料力学的任务所必需的途径和 手段。
目录
10
§1.1 材料力学的任务
四、材料力学的研究对象
m F4
m
F3
F4
F3
目录
17
§1.4 内力、截面法和应力的概念 例如
F
a
a
F
M FS
FS=F M Fa
目录
18
§1.4 内力、截面法和应力的概念
例 1.1 钻床 求:截面m-m上的内力。
解: 用截面m-m将钻床截为两部分,取上半 部分为研究对象,
受力如图:
列平衡方程:
M
Y 0 FN P
灰口铸铁的显微组织 球墨铸铁的显微组织
目录
12
§1.2 变形固体的基本假设
2、均匀性假设: 认为物体内的任何部分,其力学性能相同 普通钢材的显微组织 优质钢材的显微组织
目录
13
§1.2 变形固体的基本假设
3、各向同性假设: 认为在物体内各个不同方向的力学性能相同
(沿不同方向力学性能不同的材料称为各向异性 材料。如木材、胶合板、纤维增强材料等)
材料力学
目录
1
第一章 绪论
§1.1 材料力学的任务 §1.2 变形固体的基本假设 §1.3 外力及其分类 §1.4 内力、截面法及应力的概念 §1.5 变形与应变 §1.6 杆件变形的基本形式
目录
材料力学教学课件ppt作者范钦珊第一章材料力学概述

3. 常见组合变形的类型 : (1) 斜弯曲 (2) 拉伸(压缩)与弯曲组合 (3) 偏心拉伸(压缩) (4) 弯扭组合
计算方法 : 组合变形若忽略变形过程中各基本变形间的互相影
响,则可依据叠加原理计算。
1. 叠加原理 :弹性范围小变形情况下,各荷载分别单独 作用所产生的应力、变形等互不影响,可叠加计算。
1.7.2、剪切
(1)受力特点:杆件受到一对大小相等、 方向相反、作用线互相平行且相距很近的横 向力的作用; (2)变形特点:受剪杆件的两部分沿外 力作用方向发生相对错动;
1.7.3、扭转
(1)受力特点:杆件受到一对大小相等、方 向相反、作用面垂直于杆轴的力偶作用;
(2)变形特点:杆件的任意两个横截面发生绕轴线的相对转动。
围绕某点作一个各边分别为 、 、 的正六面体。 正六面体的x方向在力的作用下, 产生了变形 ,线 段ab 沿x方向单位长度的平均变形量为 。
平均变形量的极限:
称为点a沿x方向的的线应变 或简称应变。
由于切应力的作用,正六面体的各棱边还会发生角度的改变,当 和 趋近于零时,ab和ad所夹直角的改变量的极限
3、广义虎克定律 只有 作用时
1.7 杆件受力与变形的基本形式
材料力学的主要研究对象
杆件:长度远大于横截面尺寸的构件。 等直杆:轴线为直线且沿轴线横截面不发生变化的杆件。
杆件变形的基本形式
1.7.1、拉伸或压缩
(1)受力特点:杆件受到一对大小相等、方向相 反、作用线与杆件轴线重合的力的作用。 (2)变形特点:杆件长度方向发生伸长或缩短。
上分布内力 的合力为 ,
上分布内力的平均集度为
;
当 趋近于零时
的极限
称为点K的全应力。
材料力学(孙训方)PPT课件

[例3-2-1]已知:一传动轴, n =300r/min,主动轮输P1=500kW,
从动轮输出 P2=150kW,P3=150kW,P4=200kW,试绘制扭矩图。
m2
m3
m1
m4
解:①计算外力偶矩
m1
9.55P1 n
9.55500 300
A
15.9(kN m)
B
C
D
m 2 m 3 9 .5P n 5 2 9. 5 1 35 5 0 4 .0 0 7(8 k m N) m 49 .5P n 5 49. 5 3 25 0 0 6 0 0 .3(7km N)
单元体的四个侧面上只有剪应力而无正应力作用,这 种应力状态称为纯剪切应力状态。
四、剪切虎克定律:
其中:P n
— —
功率,马力(PS) 转速,转/分(rpm)
1PS=735.5N·m/s , 1kW=1.36PS
二、扭矩及扭矩图 1 扭矩:构件受扭时,横截面上的内力偶矩,记作“T”。 2 截面法求扭矩
mx 0 T m 0
m
m
T m
3 扭矩的符号规定:
x
m
T
“T”的转向与截面外法线方向满足右手螺旋法则为正, 反之为负。
m2
m3
m1
m4
A
B
C
T
– –
4.78 kNm
9.56 kNm
D
6.37 kNm
x
例 32-2已知 :m12kN m,m2 4kN m,m3
1kN m,m4 1kN m,求:各段扭矩及画扭
解:1——1:
m4 3 m3 2 m2 1 m1
M0 m1T10
T1 m1 2kNm
材料力学PPT课件

通常用
MPa=N/mm2 = 10 6 Pa
有些材料常数 GPa= kN/mm2 = 10 9 Pa
工程上用 kg/cm2 = 0.1 MPa
正应力s
剪应力
二、轴向拉压时横截面上应力
dA
dN dA •s
N
s dN
N dN s dA
A
A
求应力,先要找到应力在横截面上的分布情况。
应力是内力的集度,而内力与变形有关,所以
绘轴力图
(2)求应力 AB段:A1=240240mm=57600mm2
BC段:A2=370370mm=136900mm2
s1
N1 A1
50 103 57600
0.87 N
/ mm 2
0.87MPa
s2
N2 A2
150 103 136900
1.1N
/ mm 2
1.1MPa
应力为负号表示柱受压。正应力的正负号与轴力N相同。
Nl
A
l
————虎克定律(Hooke)
EA
l Pl
EA
计算中用得多
lE——N——弹性s横量(Mpa,
Gpa)
s
E
l EA E
实验中用得多
计算变形的两个实例:
1.一阶梯轴钢杆如图,AB段A1=200mm2,BC和CD段截面积相同A2=A3= 500mm2;l1= l2= l3=100mm。弹性模量E=200GPa,荷载P1=20kN,P2 =40kN 。试求:(1)各段的轴向变形;(2)全杆AD的总变形;
N1=-20kN(压) N2=-10kN(压) N3=+30kN(拉)
§3 应力
一、应力:
内力在杆件截面上某一点的密集程度
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
x
切应变(角应变)
M点处沿x方向的应变: M点在xy平面内的切应变为:
x
lim
x0
s x
g lim ( LM N)
MN0 2
ML0
类似地,可以定义 y , z ,g 均为无量纲的量。
目录
§1.5 变形与应变
例 1.2
c
已知:薄板的两条边
4、稳定性:
在载荷 作用下,构 件保持原有 平衡状态的 能力。
强度、刚度、稳定性是衡量构件承载能力 的三个方面,材料力学就是研究构件承载能力 的一门科学。
目录
§1.1 材料力学的任务
三、材料力学的任务
材料力学的任务就是在满足强度、刚度 和稳定性的要求下,为设计既经济又安全的构 件,提供必要的理论基础和计算方法。
目录
§1.3 外力及其分类
按外力与时间的关系分类
静载: 载荷缓慢地由零增加到某一定值后,就保持不变或变动很不显著, 称为静载。
动载: 载荷随时间而变化。
如交变载荷和冲击载荷
交变载荷
冲击载荷
目录
§1.4 内力、截面法和应力的概念
内力:外力作用引起构件内部的附加相互作用力。 求内力的方法 — 截面法
传统具有柱、梁、檩、椽的木 制房屋结构
建于隋代(605年)的河北赵州桥桥 长64.4米,跨径37.02米,用石2800 吨
目录
§1.1 材料力学的任务
古代建筑结构
建于辽代(1056年)的山西应县佛宫寺释迦塔 塔高9层共67.31米,用木材7400吨 900多年来历经数次地震不倒,现存唯一木塔
目录
§1.1 材料力学的任务
架的变形略去不计。计算得到很大的简
化。
C
δ1
B δ2
F
目录
§1.3 外力及其分类
外力:来自构件外部的力(载荷、约束反力)
按外力作用的方式分类
体积力:连续分布于物体内部各点 的力。如重力和惯性力
表面力:
分布力:
连续分布于物体表面上的力。如油缸内壁 的压力,水坝受到的水压力等均为分布力
Hale Waihona Puke 集中力: 若外力作用面积远小于物体表面的尺寸,可 作为作用于一点的集中力。如火车轮对钢轨 的压力等
在外力作用下,一切固体都将发生变形, 故称为变形固体。在材料力学中,对变形固体 作如下假设: 1、连续性假设: 认为整个物体体积内毫无空隙地充满物质 灰口铸铁的显微组织 球墨铸铁的显微组织
目录
§1.2 变形固体的基本假设
2、均匀性假设: 认为物体内的任何部分,其力学性能相同 普通钢材的显微组织 优质钢材的显微组织
材料力学
刘鸿文主编(第4版) 高等教育出版社
目录
第一章 绪论
目录
第一章 绪论
§1.1 材料力学的任务 §1.2 变形固体的基本假设 §1.3 外力及其分类 §1.4 内力、截面法及应力的概念 §1.5 变形与应变 §1.6 杆件变形的基本形式
目录
§1.1 材料力学的任务
一、材料力学与工程应用
古代建筑结构
目录
§1.1 材料力学的任务
四、材料力学的研究对象 构件的分类:杆件、板壳*、块体*
材料力学主要研究杆件
{ 直杆—— 轴线为直线的杆 曲杆—— 轴线为曲线的杆
{等截面杆——横截面的大小 形状不变的杆 变截面杆——横截面的大小 或形状变化的杆 等截面直杆 ——等直杆
目录
§1.2 变形固体的基本假设
例 1.1 钻床 求:截面m-m上的内力。
解: 用截面m-m将钻床截为两部分,取上半 部分为研究对象,
受力如图:
列平衡方程:
M
Y 0 FN P
Mo(F) 0
FN
Pa M 0
M Pa
目录
§1.4 内力、截面法和应力的概念
为了表示内力在一点处的强度,引入内力集度,
即应力的概念。
F A
pm
F A
M'
刚性位移; 变形位移。
2.变形
M
物体内任意两点的相对位置发生变化。
取一微正六面体
y
g
两种基本变形:
线变形
L
—— 线段长度的变化
角变形
——线段间夹角的变化 o
M
x
L'
x+s
M'
N'
N
x
目录
§1.5 变形与应变 y
g
3.应变 L'
正应变(线应变)
L
x方向的平均应变:
xm
s x
x+s
oM
x
M' N
N'
目录
§1.1 材料力学的任务
{弹性变形 — 随外力解除而消失 塑性变形(残余变形)— 外力解除后不能消失 刚度:在载荷作用下,构件抵抗变形的能力。 3、内力:构件内由于 发生变形而产生的相 互作用力。(内力随 外力的增大而增大) 强度:在载荷作用下, 构件抵抗破坏的能力。
目录
§1.1 材料力学的任务
四川彩虹桥坍塌
目录
§1.1 材料力学的任务
比萨斜塔
美国纽约马尔克大桥坍塌
§1.1 材料力学的任务
二、基本概念 1、构件:工程结构或 机械的每一组成部分。 (例如:行车结构中的 横梁、吊索等) 理论力学—研究刚体,研究力与运动的关系。 材料力学—研究变形体,研究力与变形的关系。 2、变形:在外力作用下,固体内各点相对位置的 改变。(宏观上看就是物体尺寸和形状的改变)
若:构件横截面尺寸不足或形状
不合理,或材料选用不当
___ 不满足上述要求,
不能保证安全工作.
若:不恰当地加大横截面尺寸或
选用优质材料
___ 增加成本,造成浪费
}均 不 可 取
研究构件的强度、刚度和稳定性,还需要了解材料的力学性能。因此在 进行理论分析的基础上,实验研究是完成材料力学的任务所必需的途径和 手段。
—— 平均应力
C
p lim F A0 A
—— C点的应力
p
F4
F3
F4
应力是矢量,通常分解为
C
— 正应力 — 切应力
F3
应力的国际单位为 Pa(帕斯卡) 1Pa= 1N/m2
1kPa=103N/m2 1MPa=106N/m2 1GPa=109N/m2
目录
§1.5 变形与应变
1.位移 MM'
目录
§1.2 变形固体的基本假设
3、各向同性假设: 认为在物体内各个不同方向的力学性能相同
(沿不同方向力学性能不同的材料称为各向异性 材料。如木材、胶合板、纤维增强材料等)
4、小变形与线弹性范围
A
认为构件的变形极其微小,
比构件本身尺寸要小得多。
如右图,δ远小于构件的最小尺寸,
所以通过节点平衡求各杆内力时,把支
(1)假想沿m-m横截面将
F5
杆切开
F1
(2)留下左半段或右半段
F2
(3)将弃去部分对留下部
F5
分的作用用内力代替 F1
(4)对留下部分写平衡方 F2 程,求出内力的值。
m F4
m
F3
F4
F3
目录
§1.4 内力、截面法和应力的概念 例如
F
a
a
F
M FS
FS=F M Fa
目录
§1.4 内力、截面法和应力的概念
切应变(角应变)
M点处沿x方向的应变: M点在xy平面内的切应变为:
x
lim
x0
s x
g lim ( LM N)
MN0 2
ML0
类似地,可以定义 y , z ,g 均为无量纲的量。
目录
§1.5 变形与应变
例 1.2
c
已知:薄板的两条边
4、稳定性:
在载荷 作用下,构 件保持原有 平衡状态的 能力。
强度、刚度、稳定性是衡量构件承载能力 的三个方面,材料力学就是研究构件承载能力 的一门科学。
目录
§1.1 材料力学的任务
三、材料力学的任务
材料力学的任务就是在满足强度、刚度 和稳定性的要求下,为设计既经济又安全的构 件,提供必要的理论基础和计算方法。
目录
§1.3 外力及其分类
按外力与时间的关系分类
静载: 载荷缓慢地由零增加到某一定值后,就保持不变或变动很不显著, 称为静载。
动载: 载荷随时间而变化。
如交变载荷和冲击载荷
交变载荷
冲击载荷
目录
§1.4 内力、截面法和应力的概念
内力:外力作用引起构件内部的附加相互作用力。 求内力的方法 — 截面法
传统具有柱、梁、檩、椽的木 制房屋结构
建于隋代(605年)的河北赵州桥桥 长64.4米,跨径37.02米,用石2800 吨
目录
§1.1 材料力学的任务
古代建筑结构
建于辽代(1056年)的山西应县佛宫寺释迦塔 塔高9层共67.31米,用木材7400吨 900多年来历经数次地震不倒,现存唯一木塔
目录
§1.1 材料力学的任务
架的变形略去不计。计算得到很大的简
化。
C
δ1
B δ2
F
目录
§1.3 外力及其分类
外力:来自构件外部的力(载荷、约束反力)
按外力作用的方式分类
体积力:连续分布于物体内部各点 的力。如重力和惯性力
表面力:
分布力:
连续分布于物体表面上的力。如油缸内壁 的压力,水坝受到的水压力等均为分布力
Hale Waihona Puke 集中力: 若外力作用面积远小于物体表面的尺寸,可 作为作用于一点的集中力。如火车轮对钢轨 的压力等
在外力作用下,一切固体都将发生变形, 故称为变形固体。在材料力学中,对变形固体 作如下假设: 1、连续性假设: 认为整个物体体积内毫无空隙地充满物质 灰口铸铁的显微组织 球墨铸铁的显微组织
目录
§1.2 变形固体的基本假设
2、均匀性假设: 认为物体内的任何部分,其力学性能相同 普通钢材的显微组织 优质钢材的显微组织
材料力学
刘鸿文主编(第4版) 高等教育出版社
目录
第一章 绪论
目录
第一章 绪论
§1.1 材料力学的任务 §1.2 变形固体的基本假设 §1.3 外力及其分类 §1.4 内力、截面法及应力的概念 §1.5 变形与应变 §1.6 杆件变形的基本形式
目录
§1.1 材料力学的任务
一、材料力学与工程应用
古代建筑结构
目录
§1.1 材料力学的任务
四、材料力学的研究对象 构件的分类:杆件、板壳*、块体*
材料力学主要研究杆件
{ 直杆—— 轴线为直线的杆 曲杆—— 轴线为曲线的杆
{等截面杆——横截面的大小 形状不变的杆 变截面杆——横截面的大小 或形状变化的杆 等截面直杆 ——等直杆
目录
§1.2 变形固体的基本假设
例 1.1 钻床 求:截面m-m上的内力。
解: 用截面m-m将钻床截为两部分,取上半 部分为研究对象,
受力如图:
列平衡方程:
M
Y 0 FN P
Mo(F) 0
FN
Pa M 0
M Pa
目录
§1.4 内力、截面法和应力的概念
为了表示内力在一点处的强度,引入内力集度,
即应力的概念。
F A
pm
F A
M'
刚性位移; 变形位移。
2.变形
M
物体内任意两点的相对位置发生变化。
取一微正六面体
y
g
两种基本变形:
线变形
L
—— 线段长度的变化
角变形
——线段间夹角的变化 o
M
x
L'
x+s
M'
N'
N
x
目录
§1.5 变形与应变 y
g
3.应变 L'
正应变(线应变)
L
x方向的平均应变:
xm
s x
x+s
oM
x
M' N
N'
目录
§1.1 材料力学的任务
{弹性变形 — 随外力解除而消失 塑性变形(残余变形)— 外力解除后不能消失 刚度:在载荷作用下,构件抵抗变形的能力。 3、内力:构件内由于 发生变形而产生的相 互作用力。(内力随 外力的增大而增大) 强度:在载荷作用下, 构件抵抗破坏的能力。
目录
§1.1 材料力学的任务
四川彩虹桥坍塌
目录
§1.1 材料力学的任务
比萨斜塔
美国纽约马尔克大桥坍塌
§1.1 材料力学的任务
二、基本概念 1、构件:工程结构或 机械的每一组成部分。 (例如:行车结构中的 横梁、吊索等) 理论力学—研究刚体,研究力与运动的关系。 材料力学—研究变形体,研究力与变形的关系。 2、变形:在外力作用下,固体内各点相对位置的 改变。(宏观上看就是物体尺寸和形状的改变)
若:构件横截面尺寸不足或形状
不合理,或材料选用不当
___ 不满足上述要求,
不能保证安全工作.
若:不恰当地加大横截面尺寸或
选用优质材料
___ 增加成本,造成浪费
}均 不 可 取
研究构件的强度、刚度和稳定性,还需要了解材料的力学性能。因此在 进行理论分析的基础上,实验研究是完成材料力学的任务所必需的途径和 手段。
—— 平均应力
C
p lim F A0 A
—— C点的应力
p
F4
F3
F4
应力是矢量,通常分解为
C
— 正应力 — 切应力
F3
应力的国际单位为 Pa(帕斯卡) 1Pa= 1N/m2
1kPa=103N/m2 1MPa=106N/m2 1GPa=109N/m2
目录
§1.5 变形与应变
1.位移 MM'
目录
§1.2 变形固体的基本假设
3、各向同性假设: 认为在物体内各个不同方向的力学性能相同
(沿不同方向力学性能不同的材料称为各向异性 材料。如木材、胶合板、纤维增强材料等)
4、小变形与线弹性范围
A
认为构件的变形极其微小,
比构件本身尺寸要小得多。
如右图,δ远小于构件的最小尺寸,
所以通过节点平衡求各杆内力时,把支
(1)假想沿m-m横截面将
F5
杆切开
F1
(2)留下左半段或右半段
F2
(3)将弃去部分对留下部
F5
分的作用用内力代替 F1
(4)对留下部分写平衡方 F2 程,求出内力的值。
m F4
m
F3
F4
F3
目录
§1.4 内力、截面法和应力的概念 例如
F
a
a
F
M FS
FS=F M Fa
目录
§1.4 内力、截面法和应力的概念
