ANSYS 非线性屈曲分析例子命令流
ANSYS非线性分析指南
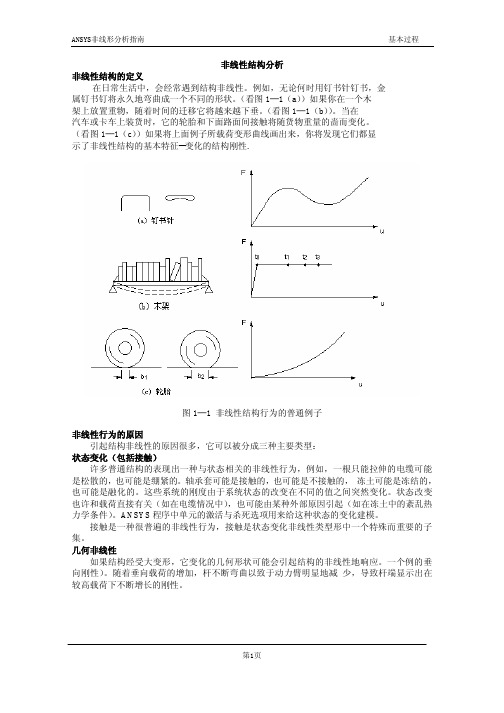
非线性结构分析非线性结构的定义在日常生活中,会经常遇到结构非线性。
例如,无论何时用钉书针钉书,金属钉书钉将永久地弯曲成一个不同的形状。
(看图1─1(a))如果你在一个木架上放置重物,随着时间的迁移它将越来越下垂。
(看图1─1(b))。
当在汽车或卡车上装货时,它的轮胎和下面路面间接触将随货物重量的啬而变化。
(看图1─1(c))如果将上面例子所载荷变形曲线画出来,你将发现它们都显示了非线性结构的基本特征--变化的结构刚性.图1─1 非线性结构行为的普通例子非线性行为的原因引起结构非线性的原因很多,它可以被分成三种主要类型:状态变化(包括接触)许多普通结构的表现出一种与状态相关的非线性行为,例如,一根只能拉伸的电缆可能是松散的,也可能是绷紧的。
轴承套可能是接触的,也可能是不接触的,冻土可能是冻结的,也可能是融化的。
这些系统的刚度由于系统状态的改变在不同的值之间突然变化。
状态改变也许和载荷直接有关(如在电缆情况中),也可能由某种外部原因引起(如在冻土中的紊乱热力学条件)。
ANSYS程序中单元的激活与杀死选项用来给这种状态的变化建模。
接触是一种很普遍的非线性行为,接触是状态变化非线性类型形中一个特殊而重要的子集。
几何非线性如果结构经受大变形,它变化的几何形状可能会引起结构的非线性地响应。
一个例的垂向刚性)。
随着垂向载荷的增加,杆不断弯曲以致于动力臂明显地减少,导致杆端显示出在较高载荷下不断增长的刚性。
图1─2 钓鱼杆示范几何非线性材料非线性非线性的应力──应变关系是结构非线性名的常见原因。
许多因素可以影响材料的应力──应变性质,包括加载历史(如在弹─塑性响应状况下),环境状况(如温度),加载的时间总量(如在蠕变响应状况下)。
牛顿一拉森方法ANSYS程序的方程求解器计算一系列的联立线性方程来预测工程系统的响应。
然而,非线性结构的行为不能直接用这样一系列的线性方程表示。
需要一系列的带校正的线性近似来求解非线性问题。
非线性屈曲分析

ansys workbench非线性屈曲分析(2013-08-26 21:26:29)转载▼标签:ansys很多旋转受压结构必须进行屈曲分析,常规结构屈曲分析软件有nastran、abaqus和ansys,nastran对线性大型模型分析效率较高;abaqus屈曲分析使用较少;ansys使用比较频繁,其快速建模,与CAD软件的良好借口及有限元模型前处理的便捷性(WB界面)很有吸引力,屈曲分析功能较为完善,可以进行线性、非线性和后屈曲分析。
ansys学习资料中介绍较多的是线性屈曲分析。
线性屈曲分析在工业实际中预测的值偏高,有的甚至超过实际实验测试值的几十倍,线性分析唯一优势是其分析速度较快。
但在实际中其预测值参考价值不大,仅给定结构屈曲失效的上限值。
非线性屈曲分析考虑其他因素,包括结构加工缺陷(几何),材料非线性等,因此较为接近实际情况,但计算耗时较长。
针对最艰难学习情况归纳总结非线性屈曲分析时技术要点及应注意事项。
对于规则旋转壳,承受外压载荷作用,进行非线性屈曲分析时,必须加上几何缺陷,关键步是添加APDL语句/prep7upgeom,0.1,1,1,file,rstcdwrite,db,file,cdb/solu该步引入屈曲模态情况下的几何缺陷,缺陷为屈曲模态变形相对值的0.1倍,该值可以根据实际加工水平等其他条件确定,上述语句保存在txt文档中,在workbench流程APDL模块调用。
分析详细流程为,static structure模块导入几何,施加载荷和边界条件,分析求解,将linear buckling拖入流程中,共享static structure模块数据,进行线性屈曲模块分析,Mechanial APDL模块调用屈曲分析结果,并调入(addinput)上面内含几何缺陷命令语句命令的txt文件,更新,将Mechanical结果导入Finite Element modeler模块,更新,此时在缺陷附近的单元节点位置发生改变。
ansys 屈曲分析详细过程

题目:跨径L=89m ,矢跨比f/L =1/5的圆弧拱,梁高h/L =1/30,梁宽b/L =1/15 求:1.弹性屈曲荷载;2.非线性极限承载能力。
1、 线性屈曲荷载理论计算在理论计算时,先根据圆弧拱的矢跨比查出稳定系数2K :表1 圆弧拱理论计算的稳定系数根据表1查得:290.4K =故其理论弹性屈曲荷载为:43723313.25105933.332966.671290.4 5.381089000xcr EI N q K m l ⨯⨯⨯⨯==⨯=⨯2、拱的弹性屈曲与非线性屈曲对于一般的特征值屈曲分析,主要是在平衡状态,考虑到轴向力或者中面内力对弯曲变形的影响,由最小势能原理,结构弹性屈曲分析归结为求解特征值问题:通过特征值分析求得的解有特征值和特征向量,特征值就是临界荷载系数,特征向量是临界荷载系数对应的屈曲模态。
特征值屈曲分析的流程图如下:[][]0D G KK λ+=图1 弹性屈曲分析流程图非线性屈曲分析是考虑结构平衡受扰动(初始缺陷、荷载扰动)的非线性静力分析,该分析是一直加载到结构极限承载状态的全过程分析,分析中可以综合考虑材料塑性和几何非线性。
结构非线性屈曲分析归结为求解矩阵方程:非线性屈曲分析的流程图如下:图2 非线性屈曲分析流程图[][](){}{}DGK K F δ+=3、非线性方程组求解方法(1)增量法增量法的实质是用分段线性的折线去代替非线性曲线。
增量法求解时将荷载分成许多级荷载增量,每次施加一个荷载增量。
在一个荷载增量中假定刚度矩阵保持不变,在不同的荷载增量中,刚度矩阵可以有不同的数值,并与应力应变关系相对应。
(2)迭代法迭代法是通过调整直线斜率对非线性曲线的逐渐逼近。
迭代法求解时每次迭代都将总荷载全部施加到结构上,取结构变形前的刚度矩阵,求得结构位移并对结构的几何形态进行修正,再用此时的刚度矩阵及位移增量求得内力增量,并进一步得到总的内力。
(3)混合法混合法是增量法和迭代法的混合使用。
ansys非线性静态分析实例命令流及GUI

非线性静态实例分析-GUI方法在这个实例分析中你将进行一个子弹冲击刚性壁的非线性分析。
问题描述一个子弹以给定的速度射向壁面壁面假定是刚性的和无摩擦的将研究子弹和壁面接触后达80微秒长的现象目的是确定子弹的整个变形速度历程以及最大等效VonMises应变求解使用SI单位用轴对称单元模拟棒求解最好能通过单一载荷步实现在这个载荷步中将同时施加初始速度和约束将圆柱体末端的节点Y方向约束住以模拟一固壁面打开自动时间分步来允许ANSYS确定时间步长定义分析结束的时间为8E-5秒以确保有足够长的时间来扑捉整个变形过程问题详细说明下列材料性质应用于这个问题EX=117.0E09(杨氏模量DENS=8930.0密度NUXY=0.35泊松比YieldStrength=400.0OE06屈服强度TangentModulus剪切模量下列尺寸应用于这个问题长=32.4E-3m直径=6.4E-3m对于这个问题的初始速度是227.0。
问题的草图:求解步骤步骤一:设置分析标题1选择菜单路径:UtilityMenn>File>ChangeTitle2键入文字:"CopperyCylinderImpactingaRigidWall"3单击OK步骤二:定义单元类型1选择菜单路径:MailMenu>Preprocessor>ElementType>All/Edit/Delete2单击:AddLibraryofElementTypes(出现单元类型库选择对话框)。
3在靠近左边的列表中单击VisioSolid,仅一次。
4选靠近右边的列表中单击4nodePlas106,仅一次。
5单击OK,LibraryofElementTypes对话框关闭。
6单击Options(选项),出现VISCO106elementtypeOptions(visco106单元类型选项)对话框。
7在关于elementbehavior(单元特性)的卷动条中,卷动到Axisymmetric,且选中它。
Ansys第25例非线性分析综合应用实例

第25例非线性分析综合应用实例----钢板卷制成圆筒本例介绍了综合利用ANSYS非线性分析功能模拟将钢板卷制成圆筒的方法和步骤。
25.1问题描述将钢板卷制成圆筒一般要使用卷板机。
图25-1所示为对称式三辊卷板机,该机器将钢板卷制成圆筒时分为三个步骤:首先,上辊下降使钢板发生挠曲,钢板挠曲线的最低点首先发生屈服;然后,下辊转动驱动钢板向前移动,使钢板各点发生同样的屈服形成圆筒;最后,圆筒卷制完成,上辊上升卸下筒体。
图25-1对称式三辊卷板机用ANSYS模拟将钢板卷制成圆筒,相应地也分为三个步骤。
由于第二个步骤需要模拟上、下辊转动,而ANSYS的SOLIDn单元不支持大转动,位移边界条件不能施加大的转动角度,所以上、下辊需要用壳单元建立有限元模型。
上、下辊与钢板的作用需要用接触模拟,钢板卷制成圆筒材料发生屈服,产生大变形, 所以钢板卷制成圆筒包括状态非线性、材料非线性和结构非线性三种非线性。
用ANSYS模拟将钢板卷制成圆筒,计算结果可以得到圆筒直径与上辊下压量的关系,上、下辊受力大小,上、下辊的变形,下辊驱动力矩及卸载回弹等重25.2 命令流/CLEAR/FILNAM, EXAMPLE25/CONFIG, NRES, 2000/PREP7/PNUM, VOLU, ONET, 1, SHELL181ET, 2, SOLID186MP, EX, 1, 2E11MP, DENS, 1, 7800MP, NUXY, 1, 0.3MP, EX, 2, 2E11MP, DENS, 2, 7800MP, NUXY, 2, 0.3TB, BKIN, 2, 1TBTEMP, 0TBDATA,, 240E6, 0 SECTYPE, 1, SHELL SECDATA, 0.02CYLIND, 0.38/2, 0, 0.2, 1.7, 0, 360 要数据。
因为分析过程复杂,步骤较多,所以本例只采用命令流法执行命令。
!清除数据库,新建文件! 指定任务名为?EXAMPLE25 “!设置最大子步数!前处理!进入前处理器!打开体号!选择单元类型,壳单元用于划分上、下辊!实体单元用于划分钢板!定义材料模型 1 的弹性模量! 定义材料模型 1 的密度!定义材料模型 1 的泊松比!定义材料模型 2 的弹性模量! 定义材料模型 2 的密度!定义材料模型 2 的泊松比! 定义材料模型 2 的屈服极限、切向模量!定义截面!壳厚度!创建上辊,圆柱体!黏结!创建右下辊,圆柱体WPOFF, -0.54!偏移工作平面原点到左下辊中心!创建左下辊,圆柱体ALLS VDELE, ALL!在上辊端面中心处创建硬!在左下辊端面中心处创CYLIND, 0.38/4, 0, 0.2, 0, 0, 360 CYLIND, 0.38/4, 0, 1.7, 1.9, 0, 360 VGLUE, ALL VSEL, NONECYLIND, 0.3/2, 0, 0.2, 1.7, 0, 360CYLIND, 0.3/4, 0, 0.2, 0, 0, 360 CYLIND, 0.3/4, 0, 1.7, 1.9, 0, 360VGLUE, ALL VSEL, NONECYLIND, 0.3/2, 0, 0.2, 1.7, 0, 360CYLIND, 0.3/4, 0, 0.2, 0, 0, 360 CYLIND, 0.3/4, 0, 1.7, 1.9, 0, 360VGLUE, ALL !选择所有实体 !删除体,但保留面 ,HPTCREATE, AREA, 5,, COORDHPTCREATE, AREA, 10,, COORD, 0, 0, 1.9HPTCREATE, AREA, 34,, COORD, -0.54/2, -0.37, 1.9WPOFF, 0.54/2, -0.37!偏移工作平面原点到右下辊中心点八、、建硬点!在右下辊端面中心处创MAT, 1 TYPE, 1 SECN, 1 ESIZE, 0.04 SMRTSIZE, 7MSHAPE, 1AMESH, ALLBLOCK, 0.7, -0.5, 0.3/2, 0.3/2+0.03, 0.5,LESIZE, 96,,, 2MAT, 2 TYPE, 2 MSHKEY, 1 MSHAPE, 0 ESIZE, 0.05 VMESH, ALL ET, 4, TARGE170 ET, 5, CONTA174,,,,,1 KEYOPT, 5, 12, 1HPTCREATE, AREA, 29,, COORD, -0.54/2, -0.37, 0 HPTCREATE, AREA, 22,, COORD, 0.54/2, -0.37, 1.9建硬点HPTCREATE, AREA, 17,, COORD, 0.54/2, -0.37, 0 !为上、 下辊划分单元指定属性, 材料模型 !单元类型 !壳横截面!指定单元边边长度!指定智能尺寸级别!指定单元形状为三角形!对所有面划分单元1.4!创建钢板,块!指定线 96 ( 钢板厚度 )被划分为两段!为钢板划分单元指定属性!映射网格!指定单元形状为六面体 !指定单元边长度 !对块划分网格!指定单元类型,用于创建接触对!设置单元 5 接触表面无滑动R, 10,,,0.1!在钢板上表面和上辊表面建立接触对!在钢板下表面和左下辊表面建立接触对!定义实常数, KFN==0.1R, 11,,, 0.1 R, 12,,, 0.1 ASEL, S,,,40 NSLA, S, 1NSEL, U, LOC, Z, 0.8, 1.1 MAT, 3 REAL, 10 TYPE, 4 ESURF ALLSASEL, S,,, 3, 4, 1 NSLA, S, 1NSEL, U, LOC, Z, 0.2,0.5 NSEL, U, LOC, Z, 0.8, 1.1 NSEL, U, LOC, Z,1.4, 1.7 MAT, 3 REAL, 10 TYPE, 5 ESURF ALLS ASEL, S,,,39NSEL, U, LOC, Z, 0.8, 1.1MAT, 4REAL, 11TYPE, 4ESURFALLSASEL, S,,, 27, 28, 1NSLA, S, 1NSEL, U, LOC, Z, 0.2, 0.5NSEL, U, LOC, Z, 0.8, 1.1NSEL, U, LOC, Z, 1.4, 1.7MAT, 4REAL, 11TYPE, 5ESURFALLSASEL, S,,, 39NSLA, S, 1 !在钢板下表面和右下辊表面建立接触对NSEL, U, LOC, Z, 0.8, 1.1MAT, 4REAL, 12!进入求解器!在所有节点点上施加约束!选择上辊轴线上的节点! 施加约束,上辊下降 0.03mESURF ALLSASEL, S,,, 15, 16, 1 NSLA, S, 1NSEL, U, LOC, Z,0.2,0.5 NSEL, U, LOC, Z,0.8,1.1 NSEL, U, LOC, Z,1.4,1.7 MAT, 4 REAL, 12 TYPE, 5 ESURF ALLS FINI!首先模拟下辊不动,上辊下降 /SOLU D, ALL, UZ D, ALL, ROTX D, ALL, ROTY NSEL, S, LOC, X NSEL, R, LOC, Y D, ALL, UY, -0.03D, ALL, UXD, ALL, UZ ALLSCSYS, 4ASEL, S, LOC, Y, -2, 0.3/2 ASEL, U,,,39NSLA, S, 1D, ALL, ALLALLSANTYPE, TRANSLNSRCH, ONNLGEOM, ONTIME, 1AUTOT, ONNSUBST, 15,20, 10KBC, 0OUTRES, ALL, ALLSOLVE!以下模拟下辊转动,驱动钢板前进CSYS, 4ASEL, S, LOC, Y, -2, 0.3/2 ASEL,U,,,39 !激活工作平面坐标系!选择下辊上的所有面!选择下辊上的所有节点!约束掉所有自由度!瞬态分析!打开线性搜索!打开大变形选项!指定载荷步时问!打开自动载荷步长!指定子步数目!斜坡载荷!输出所有子步所有项旧的结果!解答!选择下辊上的所有面NSLA, S, 1 !选择下辊上的所有节点DDELE, ALL, ALL!删除上一载荷步施加在下辊上的所有约束ALLSD, ALL, UZ !在所有节点上施加约束D, ALL, ROTXD, ALL, ROTYNSEL, S, LOC, X, 0 !选择左下辊轴线上的所有节点NSEL, R, LOC, YD, ALL, ROTZ, -3.1415926/2 !转动1/4 周D, ALL, UX !约束掉移动D, ALL, UYALLSWPOFF, 0.54 !偏移工作平面NSEL, S, LOC, X, 0 !选择右下右下辊轴线上的所有节点NSEL, R, LOC, YD, ALL, UX !约束掉移动D, ALL, UYD, ALL, ROTZ, -3.1415926/2 ! 转动1/4 周TIME, 2ALLSKBC, 0NSUBST, 800, 1000, 300!解答!查看结果!读最后载荷子步计算结果!变形云图!用动画查看卷制圆筒过程中的变形情况SOLVE!模拟卸载 ACEL, 0, 9.8 CSYS, 0NSEL, S, LOC, X NSEL, R, LOC, YD, ALL, UY, 0 D, ALL, UX D, ALL, UZ D, ALL, ROTX D, ALL, ROTY ALLS KBC, 0NSUBST, 20, 300, 10 TIME, 2.1 SOLVE FINI/POST1 SET, LASTPLNS, U, SUMANTIME, 50, 0.5,, 1, 2, 0, 2.1!施加重力加速度 !激活全球直角坐标系 !选择上辊轴线上的所有节点!上辊向上移动,卸载。
Ansys-第21例非线性屈曲分析实例

第21例非线性屈曲分析实例—悬臂梁本例通过计算悬臂梁的临界载荷,介绍了利用ANSYS进行非线性屈曲分析的方法、步骤和过程。
21.1非线性屈曲分析过程1.建立模型非线性屈曲分析的建模过程与其他分析相似,包括选择单元类型、定义单元实常数、定义材料特性、定义横截面、建立几何模型和划分网格等。
2.求解(1)进入求解器。
(2)指定分析类型。
非线性屈曲分析属于非线性静力学分析。
(3)定义分析选项。
激活大变形效应。
(4)施加初始几何缺陷或初始扰动。
可以先进行线性屈曲分析,将分析所得到的屈曲模态形状乘以一个较小的系数后作为初始扰动施加到结构上,本例即采用该方法。
(5)施加载荷。
所施加的载荷应比预测值高10%一21%。
(6)定义载荷步选项。
(7)设置弧长法。
(8)求解。
3.查看结果在POST26时间历程后处理器中,建立载荷和位移关系曲线,从而确定结构的临界载荷。
21.2问题描述及解析解图21-1 (a)所示为一悬臂梁,图21-1 (b)为梁的横横截面形状,分析其在集中力P作用下的临界载荷。
已知截面各尺寸分别为H=50mm、h=43mm、B=35mm、b=32mm,梁的长度L=1m。
钢的弹性模量E=2xl011N/m2,泊松比p=0.3。
图21-1工子悬臂梁21.3分析步骤21.3.1改变任务名拾取菜单Utility Menu→Jobname,弹出如图21-2所示的对话框,在“[/FJLNAM]”文本框中输入EXAMPLE21,单击“OK”按钮。
21.3.2选择单元类型拾取菜单Main Menu→Preprocessor→Element Type→Add/Edit/Delete,弹出如图21-3所示的对话框,单击“Add.”按钮,弹出如图21-4所示的对话框,在左侧列表中选“Structural Beam”,在右侧列表中选“3 node 189”,单击“OK”按钮,返回到如图21-3所示的对话框,单击“Close”按钮。
ansys 屈曲分析详细过程

非线性屈曲分析的流程图如下:
图 2 非线性屈曲分析流程图
2
3、非线性方程组求解方法 (1)增量法 增量法的实质是用分段线性的折线去代替非线性曲线。增量法求解时将荷载
分成许多级荷载增量,每次施加一个荷载增量。在一个荷载增量中假定刚度矩阵 保持不变,在不同的荷载增量中,刚度矩阵可以有不同的数值,并与应力应变关 系相对应。
图 4 荷载及拱的几何尺寸示意
几何尺寸: f/L=1/5, H/L=1/30,B/图L=图1图/15
L=89m,f=17.8m,H=2.97m,B=5.93m,R=64.5m
材料性能:拱圈采用 C40 混凝土,弹性模量为 32500MPa,泊松比为 0.3。
在 ANSYS 中进行建模分析,初始荷载为 q=100000kN/m 其过程如下:
0.5
K2
58.9
90.4
93.4
86.7
64.0
根据表 1 查得:
K2 90.4
故其理论弹性屈曲荷载为:
qcr
K2
EI x l3
3.25104 1 5933.33 2966.673
90.4
12 890003
5.38107
N
m
2、拱的弹性屈曲与非线性屈曲 对于一般的特征值屈曲分析,主要是在平衡状态,考虑到轴向力或者中面内
力对弯曲变形的影响,由最小势能原理,结构弹性屈曲分析归结为求解特征值问 题:
KD KG 0
通过特征值分析求得的解有特征值和特征向量,特征值就是临界荷载系数, 特征向量是临界荷载系数对应的屈曲模态。
特征值屈曲分析的流程图如下:
1
图 1 弹性屈曲分析流程图
非线性屈曲分析是考虑结构平衡受扰动(初始缺陷、荷载扰动)的非线性静 力分析,该分析是一直加载到结构极限承载状态的全过程分析,分析中可以综合 考虑材料塑性和几何非线性。结构非线性屈曲分析归结为求解矩阵方程:
ANSYS命令流学习笔记非线性屈曲分析

A N S Y S命令流学习笔记非线性屈曲分析The Standardization Office was revised on the afternoon of December 13, 2020!ANSYS命令流学习笔记9 –非线性屈曲分析!学习重点:!1、熟悉beam单元的建模!2、何为非线性屈曲分析Eigen Buckling首先了解屈曲问题。
在理想化情况下,当F < Fcr时, 结构处于稳定平衡状态,若引入一个小的侧向扰动力,然后卸载, 结构将返回到它的初始位置。
当F > Fcr时, 结构处于不稳定平衡状态, 任何扰动力将引起坍塌。
当F = Fcr时,结构处于中性平衡状态,把这个力定义为临界载荷。
在实际结构中, 几何缺陷的存在或力的扰动将决定载荷路径的方向。
在实际结构中, 很难达到临界载荷,因为扰动和非线性行为, 低于临界载荷时结构通常变得不稳定。
要理解非线性屈曲分析,首先要了解特征值屈曲。
特征值屈曲分析预测一个理想线弹性结构的理论屈曲强度,缺陷和非线性行为阻止大多数实际结构达到理想的弹性屈曲强度,特征值屈曲一般产生非保守解, 使用时应谨慎。
非线性屈曲分析时考虑结构平衡受扰动(初始缺陷、载荷扰动)的非线性静力分析,该分析时一直加载到结构极限承载状态的全过程分析,分析中可以综合考虑材料塑性、几何非线性、接触、大变形。
非线性屈曲比特征值屈曲更精确,因此推荐用于设计或结构的评价。
!3、非线性屈曲分析的理论计算及有限元计算!理论解,根据Euler公式。
其中μ取决于固定方式。
!有限元方法,已知在特征值屈曲问题:求解,即可得到临界载荷而非线性屈曲问题:其中为结构初始刚度,为有缺陷的结构刚度,{δ}为位移矩阵,{F}为载荷矩阵。
!4、弧长法的介绍(图片摘于ansys培训教程)如上分析,特征值屈曲分析得到的是非保守解,具有两个优点:快捷分析,屈曲模态形状可用作非线性屈曲分析的初始几何缺陷。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
For this solution method, ANSYS uses the linear Eigenvalue method to solve for the buckling load. The Following is a command prompt used to run the Eigenvalue method on ANSYS.
It is important to understand what the NLGEOM command does, and how it does it. This command allows ANSYS to engage in a non-linear elastic modeling of the beam.
The first Equation is the Plastic strain equation:
Where the super script “pl” represents the plastic strain, and “el” represents the linear strain, and Ԑn is the original strain. To calculate the linear strain the following equation is used:
In the previous equation Represents the equivalent total strain measure and is calculated using the following equation:
As can be seen in the equation, as the number of iterations are increased, the magnitude of the plastic deformation decreases (in a new iteration, the results for the plastic strain is used as the initial strain). The rate of the decrease also decreases with an increasing number of iterations, until the answer for the strain converges. This however does not take into account Non-linear Young modulus, and more complicated methods must be used in order to compute the stress-strain of a model with a non-linear Young’s modulus.
Beams Rods Columns Crankshafts Piston and Cylinders Synthetic bones and prosthetics. Any mechanism that undergoes compression
Finite Element Analysis allows the Solution of buckling problems. The Column is divided into different nodes and a small preload is added. ANSYS offers 2 buckling modes, Eigenvalue (Linear) and a non-linear solution method. Nhomakorabea
ANSYS can also produce non-linear results. This is done by using sub-stepped loads, to calculate the strains and getting a new Young’s Modulus with the given strain. An initial deformation is placed in the model, so that ANSYS may bend the model and simulate buckling (otherwise the load would show only compressive results). The next is a command prompt to input in ANSYS to produce the analysis.
Buckling is the failure of columns and rods when under a compressive load. The rod/column/beam bends before the load reaches the material’s yield point. Buckling occurs due to the structure’s imperfections.
ANSYS produces Favorable results for buckling Analysis. The non-linear Buckling analysis tends to give more conservative results as seen in the figures. Care must be taken, as sometimes non-linear problems may not converge.
