ANSYS非线性分析高级讲义
Ansys16.1非线性分析官方培训教程Mechanical-Nonlin_13.0_Ch01_Overview

Release 13.0 December 2010
ANSYS Mechanical Structural Nonlinearities
Chapter Overview
•
Customer Training Material
In this chapter, an overview of the basics of nonlinear finite-element analysis (FEA) is presented:
Customer Training Material
• How does Workbench Mechanical solve for a changing stiffness?
– In a nonlinear analysis, the response cannot be predicted directly with a set of linear equations. – However, a nonlinear structure can be analyzed using an iterative series of linear approximations, with corrections. – ANSYS uses an iterative process called the Newton-Raphson Method. Each iteration is known as an equilibrium iteration.
F = Ku
– The constant K represents structural stiffness.
• A linear structure obeys this linear relationship. A common example is a simple spring:
ANSYS 高级技术分析:非线性_结构分析
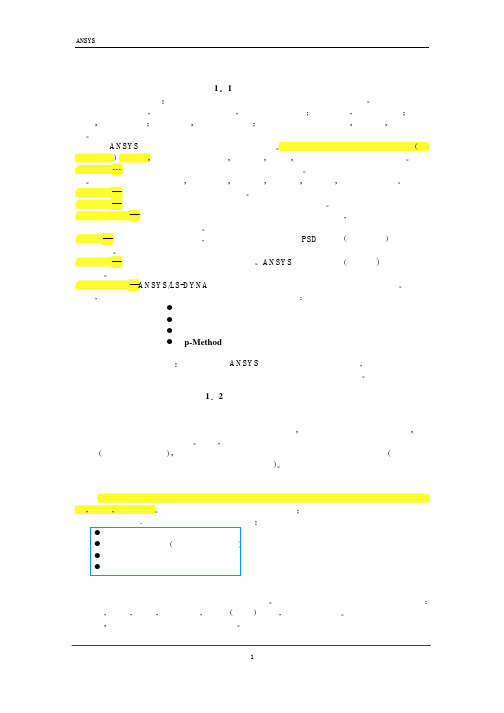
第一章结构静力分析1 1 结构分析概述结构分析的定义结构分析是有限元分析方法最常用的一个应用领域结构这个术语是一个广义的概念它包括土木工程结构如桥梁和建筑物汽车结构如车身骨架海洋结构如船舶结构航空结构如飞机机身等同时还包括机械零部件如活塞传动轴等等在ANSYS产品家族中有七种结构分析的类型结构分析中计算得出的基本未知量节点自由度是位移其他的一些未知量如应变应力和反力可通过节点位移导出静力分析---用于求解静力载荷作用下结构的位移和应力等静力分析包括线性和非线性分析而非线性分析涉及塑性应力刚化大变形大应变超弹性接触面和蠕变模态分析---用于计算结构的固有频率和模态谐波分析---用于确定结构在随时间正弦变化的载荷作用下的响应瞬态动力分析---用于计算结构在随时间任意变化的载荷作用下的响应并且可计及上述提到的静力分析中所有的非线性性质谱分析---是模态分析的应用拓广用于计算由于响应谱或PSD输入随机振动引起的应力和应变曲屈分析---用于计算曲屈载荷和确定曲屈模态ANSYS可进行线性特征值和非线性曲屈分析显式动力分析---ANSYS/LS-DYNA可用于计算高度非线性动力学和复杂的接触问题此外前面提到的七种分析类型还有如下特殊的分析应用断裂力学复合材料疲劳分析p-Method结构分析所用的单元绝大多数的ANSYS单元类型可用于结构分析单元型从简单的杆单元和梁单元一直到较为复杂的层合壳单元和大应变实体单元1 2 结构线性静力分析静力分析的定义静力分析计算在固定不变的载荷作用下结构的效应它不考虑惯性和阻尼的影响如结构受随时间变化载荷的情况可是静力分析可以计算那些固定不变的惯性载荷对结构的影响如重力和离心力以及那些可以近似为等价静力作用的随时间变化载荷如通常在许多建筑规范中所定义的等价静力风载和地震载荷静力分析中的载荷静力分析用于计算由那些不包括惯性和阻尼效应的载荷作用于结构或部件上引起的位移应力应变和力固定不变的载荷和响应是一种假定即假定载荷和结构的响应随时间的变化非常缓慢静力分析所施加的载荷包括外部施加的作用力和压力稳态的惯性力如中力和离心力位移载荷温度载荷线性静力分析和非线性静力分析静力分析既可以是线性的也可以是非线性的非线性静力分析包括所有的非线性类型大变形塑性蠕变应力刚化接触间隙单元超弹性单元等本节主要讨论线性静力分析非线性静力分析在下一节中介绍第1页线性静力分析的求解步骤1建模2施加载荷和边界条件求解3结果评价和分析目录非线性结构分析的定义 1非线性行为的原因 1非线性分析的重要信息 3非线性分析中使用的命令8非线性分析步骤综述8 第一步建模 9第二步加载且得到解 9第三步考察结果16非线性分析例题GUI方法 20第一步设置分析标题 21第二步定义单元类型21第三步定义材料性质22第四步定义双线性各向同性强化数据表22第五步产生矩形22第六步设置单元尺寸23第七步划分网格23第八步定义分析类型和选项23第九步定义初始速度24第十步施加约束24第十一步设置载荷步选项24第十二步求解25第十三步确定柱体的应变25第十四步画等值线26第十五步用Post26定义变量26第十六步计算随时间变化的速度26非线性分析例题命令流方法 271 3 非线性结构静力分析非线性结构的定义在日常生活中,会经常遇到结构非线性例如无论何时用钉书针钉书金属钉书钉将永久地弯曲成一个不同的形状看图1─1a如果你在一个木架上放置重物随着时间的迁移它将越来越下垂看图1─1b当在汽车或卡车上装货时它的轮胎和下面路面间接触将随货物重量的啬而变化看图1─1c如果将上面例子所载荷变形曲线画出来,你将发现它们都显示了非线性结构的基本特征--变化的结构刚性.图1─1 非线性结构行为的普通例子非线性行为的原因引起结构非线性的原因很多它可以被分成三种主要类型状态变化包括接触许多普通结构的表现出一种与状态相关的非线性行为,例如一根只能拉伸的电缆可能是松散的,也可能是绷紧的轴承套可能是接触的,也可能是不接触的, 冻土可能是冻结的,也可能是融化的这些系统的刚度由于系统状态的改变在不同的值之间突然变化状态改变也许和载荷直接有关如在电缆情况中也可能由某种外部原因引起如在冻土中的紊乱热力学条件ANSYS程序中单元的激活与杀死选项用来给这种状态的变化建模接触是一种很普遍的非线性行为接触是状态变化非线性类型形中一个特殊而重要的子集几何非线性它变化的几何形状可能会引起结构的非线性地响应一个例的垂向刚性随着垂向载荷的增加杆不断弯曲以致于动力臂明显地减少导致杆端显示出在较高载荷下不断增长的刚性图1─2 钓鱼杆示范几何非线性材料非线性许多因素可以影响材料的应力第4页──应变性质包括加载历史如在弹─塑性响应状况下环境状况如温度加载的时间总量如在蠕变响应状况下牛顿一拉森方法ANSYS程序的方程求解器计算一系列的联立线性方程来预测工程系统的响应然而非线性结构的行为不能直接用这样一系列的线性方程表示需要一系列的带校正的线性近似来求解非线性问题逐步递增载荷和平衡迭代一种近似的非线性救求解是将载荷分成一系列的载荷增量可以在几个载荷步内或者在一个载步的几个子步内施加载荷增量在每一个增量的求解完成后继续进行下一个载荷增量之前程序调整刚度矩阵以反映结构刚度的非线性变化遗憾的是纯粹的增量近似不可避免地随着每一个载荷增量积累误差导种结果最终失去平衡如图1─3a所示所示.a 纯粹增量式解b)全牛顿拉普森迭代求解2个载荷增量图8─3 纯粹增量近似与牛顿拉普森近似的关系ANSYS程序通过使用牛顿拉普森平衡迭代克服了这种困难它迫使在每一个载荷增量的末端解达到平衡收敛在某个容限范围内图1─3b)描述了在单自由度非线性分析中牛顿拉普森平衡迭代的使用在每次求解前NR方法估算出残差矢量这个矢量是回复力对应于单元应力的载荷和所加载荷的差值程序然后使用非平衡载荷进行线性求解且核查收敛性如果不满足收敛准则重新估算非平衡载荷修改刚度矩阵获得新解持续这种迭代过程直到问题收敛ANSYS程序提供了一系列命令来增强问题的收敛性如自适应下降线性搜索自动载荷步及二分等可被激活来加强问题的收敛性如果不能得到收敛那么程序或者继续计算下一个载荷前或者终止依据你的指示对某些物理意义上不稳定系统的非线性静态分析如果你仅仅使用NR方法正切刚度矩阵可能变为降秩短阵导致严重的收敛问题这样的情况包括独立实体从固定表面分离的静态接触分析结构或者完全崩溃或者突然变成另一个稳定形状的非线性弯曲问题对这样的情况你可以激活另外一种迭代方法弧长方法来帮助稳定求解弧长方法导致NR平衡迭代沿一段弧收敛从而即使当正切刚度矩阵的倾斜为零或负值时也往往阻止发散这种迭代方法以图形表示在图1─4中图1─4传统的NR方法与弧长方法的比较非线性求解的组织级别非线性求解被分成三个操作级别载荷步子步平衡迭代顶层级别由在一定时间范围内你明确定义的载荷步组成假定载荷在载荷步内是线性地变化的在每一个载荷是步内为了逐步加载可以控制程序来执行多次求解子步或时间步在每一个子步内程序将进行一系列的平衡迭代以获得收敛的解图1─5说明了一段用于非线性分析的典型的载荷历史图1─5载荷步子步及时间收敛容限当你对平衡迭代确定收敛容限时你必须答这些问题你想基于载荷变形还是联立二者来确定收敛容限既然径向偏移以弧度度量比对应的平移小你是不是想对这些不同的条目建立不同的收敛准则当你确定收敛准则时ANSYS程序会给你一系列的选择你可以将收敛检查建立在力力矩位移转动或这些项目的任意组合上另外每一个项目可以有不同的收敛容限值对多自由度问题你同样也有收敛准则的选择问题当你确定你的收敛准则时记住以力为基础的收敛提供了收敛的绝对量度而以位移为基础的收敛仅提供了表观收敛的相对量度因此你应当如果需要总是使用以力为基础或以力矩为基础的收敛容限如果需要可以增加以位移为基础或以转动为基础的收敛检查但是通常不单独使用它们图1─6说明了一种单独使用位移收敛检查导致出错情况在第二次迭代后计算出的位移很小可能被认为是收敛的解尽管问题仍旧远离真正的解要防止这样的错误应当使。
ANSYS讲义-非线性分析

FORCE CONVERGENCE VALUE = 4.687
CRITERION= 2.113
DISP CONVERGENCE VALUE = 0.1024E-01 CRITERION= 0.9406 <<< CONVERGED
EQUIL ITER 3 COMPLETED. NEW TRIANG MATRIX. MAX DOF INC= 0.3165E-02
也就是每一迭代步的求解误差与前一步误差的平 方成正比。
XJTU
2) 收 敛
Newton-Raphson 法需要一个收敛的度量以决定何时 结束迭代。给定外部载荷(Fa),内部载荷( Fnr )( 由单元应力产生并作用于节点),在一个体中,外部载 荷必须与内力相平衡。
Fa - Fnr = 0
收敛是平衡的度量。
在这个接触例题中 ,接触面积未知, 它取决与施加载荷 的大小。
XJTU
非线性分析得到的结果
• 不能使用叠加原理! • 结构响应与路径有关,也就是说加载的顺序可能是
重要的。 • 结构响应与施加的载荷可能不成比例。
XJTU
非线性分析的应用
• 一些典型的非线性分析的应用包括:
– 非线性屈曲失稳分析 – 金属成形研究 – 碰撞与冲击分析 – 制造过程分析( 装配、部件接触等) – 材料非线性分析 (弹性材料、聚合物) – 承受极限载荷的系统分析(塑性行为与动力响应)
• 力/力矩不平衡量 {R}
FORCE CONVERGENCE VALUE
• 最大的自由度增量 {u}
MAX DOF INC
• 力收敛判据
CRITERION
• 载荷步与子步数
LOAD STEP 1 SUBSTEP 14
ansys高级非线性分析-第三章_高级率无关塑性

1 0 0 0 0 0
0 1 0 0 0 0 s m m m
M
0 0
0 0
1 0
0 2
0 0
0 0
0 0 0 0 2 0
m
1 3
x y z
0 0 0 0 0 2
00
0
September 30, 2001 Inventory #001491 3-14
Advanced Structural Nonlinearities 6.0
弹性回顾:
• 讨论塑性之前,先回顾一下金属的弹性。
– 弹性响应中,如果产生的应力低于材料的屈服点,卸载时材料可完全 恢复到原来的形状。
– 从金属的观点看,这种行为是因为延伸但没有破坏原子间化学键。因 为弹性是由于原子键的延伸,所以是完全可恢复的。而且这些弹性应 变往往是小的。
– 金属的弹性行为最常用虎克定律的应力应变关系描述:
屈服点 y
卸载
弹性
塑性
September 30, 2001 Inventory #001491 3-6
Advanced Structural Nonlinearities 6.0
率无关塑性
... 塑性背景
Training Manual
率无关塑性:
• 如果材料响应和载荷速率或变形速率无关,称材料为率无关 。
率无关塑性
... Mises 屈服准则
Training Manual
• 应力状态可分解为静水压力(膨胀)和偏差(变形)分量。
– 静水压应力和体积改变能有关,而偏差应力和形状改变有关。
• von Mises 屈服准则说明只有偏差分量 {s} 引起屈服。
September 30, 2001 Inventory #001491 3-15
ANSYS非线性分析

11.2 结构(jiégòu)非线性分析
➢ (4) Nonlinear标签
➢ Nonlinear标签局部(bù fen)选项及界面如表11-2及图11-4所示 。
第十六页,共204页。
11.2 结构(jiégòu)非线性分析
• 1.进入求解(qiú jiě)控制对话框 • GUI:【Main Menu】/【Solution】/【Analysis Type】/【Sol'n
Controls】 • 弹出求解(qiú jiě)控制对话框,如图11-1所示。此时的求解(qiú jiě)
用途 指定方程求解器 对于多重启动指定参数
第二十三页,共204页。
11.2 结构(jiégòu)非线性分析
图11-3 Sol'n Options标签(biāoqiān)界面
第二十四页,共204页。
11.2 结构(jiégòu)非线性分析
• ANSYS的自动求解控制在大多数情况下,激活稀疏矩阵直接求解器,即缺 省的求解器,其他选项包括(bāokuò)直接求解器和PCG求解器。对于在三 维模型中实体单元使用PCG求解器可能更快。假设用PCG求解器,而且是 小应变静力或完全瞬态分析,可以考虑用MSAVE命令降低内存应用。其他 情况,可用刚度矩阵的总体安装来求解。对于符合上述条件的结构,用 MSAVE,ON 可能可节省70%的内存,但求解时间可能增加,这与计算机的 配置和CPU速度有关。稀疏矩阵求解器是一个健壮的求解器。虽然PCG求 解器能够求解同样的矩阵方程,但在它碰到一个病态矩阵时,求解器将反 复指定的迭代数目,并在收敛失败时停止。在发生这种问题时,它触发二 分。在完成二分后,求解器继续求解,如果结果矩阵是良态的话,最后可 以求解整个非线性载荷步。稀疏矩阵求解器在梁、壳或者梁、壳、实体结 构,病态问题,不同区域材料特性相差巨大的模型以及位移边界条件缺乏 的情况下可得到满意解;PCG求解器在三维结构且自由度数相对较大时使 用。
ansys高级非线性分析-第六章_超弹性解读

September 30, 2001 Inventory #001491 6-7
超弹性
... 延伸率的定义
Training Manual
Advanced Structural Nonlinearities 6.0
• 举例说明主延伸率的定义, 考虑一个薄正方形橡胶薄板进行双向拉 伸,主延伸率 l1 和 l2 描述了平面内变形特征,另一方面, l3 定义 厚度变化 (t/to),另外, 若材料假设为完全不可压缩, 则 l3 等于l-2.
Training Manual
Advanced Structural Nonlinearities 6.0
• 由于材料的不可压缩性, 把应变能函数分解为偏差项(下标d 或‘bar’ )和体积项(下标b),结果, 体积项仅为体积比J 的函数。
W Wd I1 , I 2 Wb J
W Wd l1 , l2 , l3 Wb J
– 与塑性不同, 超弹性不定义为速率公式
D :
– 相反, 总应力与总应变的关系由应变能势 (W)来定义。
September 30, 2001 Inventory #001491 6-6
超弹性
... 延伸率的定义
详细讨论应变能势的不同形式之前,先定义一些术语: • 延伸率(或只是‘延伸’) 定义为:
l2 l L L o
l3 t t l2 o
l1 l L L o
September 30, 2001 Inventory #001491 6-8
超弹性
... 应变不变量的定义
• 三个应变不变量一般用于定义应变能密度函数。
2 2 I1 l1 l2 l 2 3 2 2 2 2 2 I 2 l1 l2 l2 l l 2 3 3 l1 2 2 2 I 3 l1 l2 l3
ANSYS 高级技术分析:非线性_弹塑性分析

则 在土壤和脆性材料中 屈服应力是与静水压应力 侧限压力 有关的 侧限压力越高
发生屈服所需要的剪应力越大
流动准则
流动准则描述了发生屈服时 塑性应变的方向 也就是说 流动准则定义了单个塑性应
ε ε 变分量
pl
x
pl 等 随着屈服是怎样发展的
y
一般来说 流动方程是塑性应变在垂直于屈服面的方向发展的屈服准则中推导出来的
BKIN
• 双线性等向强化
BISO
• 多线性随动强化
MKIN
• 多线性等向强化
MISO
经典的双线性随动强化 BKIN 使用一个双线性来表示应力应变曲线 所以有两个斜率 弹
第3页
ANSYS
非
线
形
分
析
指
南
弹塑性分析
性斜率和塑性斜率 由于随动强化的 Vonmises 屈服准 则被使用 所以包含有鲍辛格效应
第1页
ANSYS
非
线
形
分
析
指
南
弹塑性分析
屈服准则的值有时候也叫作等效应力 一个通用的屈服准则是 Von Mises 屈服准则 当等效应力超过材料的屈服应力时 将会发生塑性变形
可以在主应力空间中画出 Mises 屈服准则 见 图 3 1
σ σ σ 在 3 D 中 屈服面是一个以 = = 为轴的圆柱面 在 2 D 中 屈服面是一
n( l )
0
大应变的塑性分析一般采用真实的应力 应变数据而小应变分析一般采用工程的应力
应变数据
什么时候激活塑性
当材料中的应力超过屈服点时 塑性被激活 也就是说 有塑性应变发生 而屈服应
力本身可能是下列某个参数的函数
• 温度 • 应变率 • 以前的应变历史 • 侧限压力 • 其它参数
ANSYS 第12讲-非线性空间

•
非线性的求解控制都在:Solution>Sol’n Control
May,25,2005
湖南大学·土木·桥梁
12-23
求解策略-自动求解控制
•
应该说,关于非线性分析的求解控制很多,如何进行选择,这是一个值得仔细分 析的问题。但是,在大多数情况下,我们只需要比较简单的步骤就可以进行非线 性分析。 在默认状态下,自动求解控制处于自动激活状态。 ——提供全面、自动及智能的非线性工具设置,一般能获得有效的收敛解。 ——一般可以解决大部分非线性问题。 ——推荐首先选用该控制选项进行非线性分析,如果收敛,则OK;若收敛速度 较慢、或者不收敛,通过调整求解选项去保证结果收敛。
ANSYS第十二讲
非线性分析
第十二讲:
非线性分析
May,25,2005
湖南大学·土木·桥梁
12-1
内容及目标
学习完本章后,能够使用ANSYS进行一些非线性的结构分析。
Part A. 非线性有限元分析的基本概念 Part B. 非线性分析的前处理 Part C. 非线性分析的求解控制 Part D. 非线性分析的后处理
• • • •
F
..
屈服点
比例极限
U
May,25,2005
湖南大学·土木·桥梁
12-9
非线性分析的建模-塑性理论
• • 两类:增量理论、全量理论 增量理论描述的是应力增量与应变增量的数学关系,是目前常用的一 种塑性分析理论。 增量理论的三个基本组成部分: 1. 屈服准则 2. 流动准则 3. 硬化准则
选择输出结果类型
为动画、结果历史写出更多 的子步结果。
May,25,2005
湖南大学·土木·桥梁
12-27
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
XJTU
非线性分析得到的结果
• 不能使用叠加原理! • 结构响应与路径有关,也就是说加载的顺序可能是
重要的。 • 结构响应与施加的载荷可能不成比例。
XJTU
非线性分析的应用
• 一些典型的非线性分析的应用包括:
– 非线性屈曲失稳分析 – 金属成形研究 – 碰撞与冲击分析 – 制造过程分析( 装配、部件接触等) – 材料非线性分析 (弹性材料、聚合物) – 承受极限载荷的系统分析(塑性行为与动力响应)
XJTU
非线性分析的应用(续)
宽翼悬臂梁的侧边扭转失 稳
一个由于几何非线性造 成的结构稳定性问题
XJTU
非线性分析的应用(续)
橡胶底密封 一个包含几何非线 性(大应变与大变 形),材料非线性 (橡胶),及状态 非线性(接触的例 子。
XJTU
非线性分析的应用(续)
轴上装配花键,接触非线性 的例子
XJTU
概述
ANSYS 最常用的非线性功能
– 几何非线性
大应变,大位移与大转动
-- 结构稳定性 (前屈曲分析与后屈曲分析)
– 塑性
– 超弹性
– 接触非线性
XJTU
非线性分析
XJTU
主要内容
应理解非线性分析中所用到的基本术语:
1. Newton-Raphson法 2. 收敛 3. 载荷步,子步和平衡迭代 4. 自动时间步 5. 输出文件信息 6. 非线性求解过程 7. 高级求解控制 8. 重启动分析
XJTU
收敛判据
• ANSYS 缺省的收敛判据是力 / 力矩和位移 / 旋转增 量。
• 对于力 / 力矩缺省的容限是0.5%,对于位移 / 旋转 增量的容限是 5% 。
• 经验表明这些容限对于大多数问题具有足够的精确 度。缺省的设置对于广泛的工程问题既不“太紧” 也不“太松”。
XJTU
收敛判据(续)
力收敛判据提供了一个收敛的绝对度量,因为它可直接度量内 部力与外部力间的平衡。
基于检查的位移判据只应作为力 收敛判据的辅助手段使用。 只依据位移判断收敛在一些情况 下将导致错误的结果。
XJTU
收敛半径
虽然使用一致切向刚度的Newton-Raphson法具有平方的收敛速度 ,但它不能保证一定收敛!只有初始构形在收敛半径以内, Newton-Raphson 才可以保证收敛。
ANSYS 及其在材料科学中的应用
(5)
XJTU
Outline 非线性分析
1. 非线性概述 2. 非线性求解
XJTU
非线性行为 基本概念
非线性结构的基本特征是结构刚度随载荷的改变而变化。如果绘制 一个非线性结构的载荷-位移曲线,则力与位移的关系是非线性函 数。
F
当载荷增加时,载荷-
位移曲线的斜率也在改
最终结果偏离平衡。
u 位移
XJTU
1) Newton-Raphson 法
ANSYS 使用Newton-Raphson平衡迭代法 克服了增量
求解的问题。 在每个载荷增量步结束时,平衡迭代驱 使解回到平衡状态。
载荷
F
4 3 2
1
u 位移
一个载荷增量中全 Newton-Raphson 迭代 求解。(四个迭代步如 图所示)
XJTU
收 敛(续)
Newton-Raphson 迭代过程如下所示。基于 u0 时的结 构构形,计算出切向刚度KT,基于F 计算出的位移增 量是u ,结构构形更新为 u1。
载荷
KT
Fa
R
F Fnr
u u0 u1
在更新的构形中计算出内力 (单元力) 。 迭代中的 Newton-Raphson 不平衡量 是:
也就是每一迭代步的求解误差与前一步误差的平 方成正比。
XJTU
2) 收 敛
Newton-Raphson 法需要一个收敛的度量以决定何时 结束迭代。给定外部载荷(Fa),内部载荷( Fnr )( 由单元应力产生并作用于节点),在一个体中,外部载 荷必须与内力相平衡。
Fa - Fnr = 0
收敛是平衡的度量。
Fa
4
3
2
1
u
XJTU
Newton-Raphson 法(续)
Newton-Raphson法是ANSYS用于求解非线性方程组
的一种数值方法 。 Newton-Raphson法基于增量加载
与迭代,使每个载荷增量步达到平衡。
Newton-Raphson 法的优点是对于一致的切向刚度矩 阵有二次收敛速度。
变。在本例中结构是“
软化”的。
u
XJTU
非线性行为(续)
引起结构非线性的原因有很多,它们可分成以下三种主 要类型:
1. 几何非线性
大应变,大位移,大旋转
2. 材料非线性
塑性,超弹性,粘弹性,蠕变
3. 状态改变非线性
接触,单元死活
XJTU
几何非线性
如果一个结构承受大的变形,它改变的几何构形可导致非线性 行为。大位移、大应变和大旋转是几何非线性的例子。
XJTU
Newton-Raphson法(续)
Newton-Raphson 法迭代求解使用下列方程: [KT]{u} = {Fa} - {Fnr}
这里:
[KT] = 切向刚度矩阵 {u} = 位移增量 {Fa} = 施加的载荷矢量 {Fnr} = 内力矢量
目标是迭代至收敛 (后面定义)。
[KT]
XJTU
非线性求解
在非线性分析中,不能直接由线性方程组求得响应。 需要将载荷分解成许多增量求解,每一增量确定一平 衡条件。
F
u
XJTU
渐变式加载
非线性求解的一种方法是将载荷分解为一系列增量。 在每一增量步求解结束后,调节刚度矩阵以适应非线 性响应。
载荷
F
累计响应
误差
纯增量法的问题在于载荷
增量步导致误差累积,使
R = Fa - Fnr
位移
XJTU
收 敛(续)
Newton-Raphson不平衡量 (Fa - Fnr) 实际上从未真 正等于零。当不平衡量小到误差允许范围内时,可中 止Newton-Raphson 迭代,得到平衡解。
在数学上,当不平衡量的范数||{Fa} - {Fnr}||小于指定 容限乘以参考力的值时就认为得到收敛。
在轻微的横向载荷下,杆的端部是极度柔性的,当载荷增加时,杆的几何 形状改变(变弯曲)并减少了力臂(由于载荷移动),从而导致杆的刚度 在较高载荷下不断增大。
XJTU
材料非线性
非线性的应力-应变关系是产生结构非线性的一个普遍原因。
应力
应力
应变
钢
应变
橡胶
XJTU
状态改变非线性
许多非线性问题是与状态相关的。例如一段绳索可以是松驰的 或拉紧的。一个装配件的两部分可能接触或脱离接触。
