ANSYS命令流学习笔记10-利用APDL在WorkBench中进行非线性屈曲分析
非线性屈曲分析
ansys workbench非线性屈曲分析(2013-08-26 21:26:29)转载▼标签：ansys很多旋转受压结构必须进行屈曲分析，常规结构屈曲分析软件有nastran、abaqus和ansys，nastran对线性大型模型分析效率较高；abaqus屈曲分析使用较少；ansys使用比较频繁，其快速建模，与CAD软件的良好借口及有限元模型前处理的便捷性（WB界面）很有吸引力，屈曲分析功能较为完善，可以进行线性、非线性和后屈曲分析。
ansys学习资料中介绍较多的是线性屈曲分析。
线性屈曲分析在工业实际中预测的值偏高，有的甚至超过实际实验测试值的几十倍，线性分析唯一优势是其分析速度较快。
但在实际中其预测值参考价值不大，仅给定结构屈曲失效的上限值。
非线性屈曲分析考虑其他因素，包括结构加工缺陷（几何），材料非线性等，因此较为接近实际情况，但计算耗时较长。
针对最艰难学习情况归纳总结非线性屈曲分析时技术要点及应注意事项。
对于规则旋转壳，承受外压载荷作用，进行非线性屈曲分析时，必须加上几何缺陷，关键步是添加APDL语句/prep7upgeom,0.1,1,1,file,rstcdwrite,db,file,cdb/solu该步引入屈曲模态情况下的几何缺陷，缺陷为屈曲模态变形相对值的0.1倍，该值可以根据实际加工水平等其他条件确定，上述语句保存在txt文档中，在workbench流程APDL模块调用。
分析详细流程为，static structure模块导入几何，施加载荷和边界条件，分析求解，将linear buckling拖入流程中，共享static structure模块数据，进行线性屈曲模块分析，Mechanial APDL模块调用屈曲分析结果，并调入（addinput）上面内含几何缺陷命令语句命令的txt文件，更新，将Mechanical结果导入Finite Element modeler模块，更新，此时在缺陷附近的单元节点位置发生改变。
ansys workbench中apdl的用法
ANSYS Workbench中的APDL（ANSYS Parametric Design Language）是一种参数化设计语言，用于在ANSYS软件中自动化建模和求解过程。
以下是APDL的一些用法：
1. 创建模型：使用APDL可以创建各种类型的模型，包括结构、流体动力学、电磁等。
在创建模型时，可以通过定义参数、约束条件和载荷等来自动化建模过程。
2. 优化设计：APDL可以用于优化设计，通过调整参数、约束条件和载荷等，获得最佳的设计方案。
3. 自动化求解：使用APDL可以自动化求解过程，包括网格划分、求解设置、结果后处理等。
4. 批处理操作：通过APDL，可以对一组模型进行批处理操作，例如批量分析、批量结果后处理等。
5. 自定义功能：使用APDL可以自定义功能，例如创建自定义的命令流、宏等，扩展ANSYS软件的功能。
在使用APDL时，需要注意以下几点：
1. 学习APDL需要一定的编程基础和数学知识。
2. 在使用APDL之前，需要了解ANSYS软件的基本操作和功能。
3. 在编写APDL脚本时，需要注意语法错误和逻辑错误，并进
行充分的测试和验证。
4. 在使用APDL进行复杂模型的分析时，需要注意计算资源和内存的分配，以确保计算过程的稳定性和效率。
ANSYS中的APDL命令
结合自身经验，谈ANSYS中的APDL命令(二)发表时间：2009-5-10 作者: 倪欣来源: e-works关键字: ANSYS APDL 命令流在ANSYS中，命令流是由一条条ANSYS的命令组成的一个命令组合，这些命令按照一定顺序排布，能够完成一定的ANSYS功能，本文是作者结合自身经验所总结的一些命令。
1.1 /prep7(进入前处理)定义几何图形：关键点、线、面、体（1）.csys,kcnkcn , 0 迪卡尔坐标系1 柱坐标2 球4 工作平面5 柱坐标系（以Y轴为轴心）n 已定义的局部坐标系（2）.numstr, label, value 设置以下项目编号的开始nodeelemkplineareavolu注意：vclear, aclear, lclear, kclear 将自动设置节点、单元开始号为最高号，这时如需要自定义起始号，重发numstr（3）.K, npt, x,y,z, 定义关键点Npt：关键点号，如果赋0，则分配给最小号（4）.Kgen,itime,Np1,Np2,Ninc,Dx,Dy,Dz,kinc,noelem,imoveItime：拷贝份数Np1,Np2,Ninc：所选关键点Dx,Dy,Dz：偏移坐标Kinc：每份之间节点号增量noelem: “0” 如果附有节点及单元，则一起拷贝。
“1”不拷贝节点和单元imove：“0” 生成拷贝“1”移动原关键点至新位置，并保持号码，此时（itime,kinc,noelem）被忽略注意：MAT,REAL,TYPE 将一起拷贝，不是当前的MAT,REAL,TYPE（5）.A, P1, P2, ……… P18 由关键点生成面（6）.AL, L1,L2, ……,L10 由线生成面面的法向由L1按右手法则决定，如果L1为负号，则反向。
（线需在某一平面内坐标值固定的面内）（7）.vsba, nv, na, sep0,keep1,keep2 用面分体（8）.vdele, nv1, nv2, ninc, kswp 删除体kswp: 0 只删除体1 删除体及面、关键点（非公用）（9）.vgen, itime, nv1, nv2, ninc, dx, dy, dz, kinc, noelem, imove 移动或拷贝体itime: 份数nv1, nv2, ninc：拷贝对象编号dx, dy, dz ：位移增量kinc: 对应关键点号增量noelem,：0：同时拷贝节点及单元1：不拷贝节点及单元imove：0：拷贝体1：移动体（10）.cm, cname, entity 定义组元，将几何元素分组形成组元cname: 由字母数字组成的组元名entity: 组元的类型（volu, area, line, kp, elem, node）（11）.cmgrp, aname, cname1, ……,cname8 将组元分组形成组元集合aname: 组元集名称cname1……cname8: 已定义的组元或组元集名称1.2 定义几个所关心的节点，以备后处理时调用节点号。
AnsysWorkbench工程应用之——结构非线性（上）：几何非线性（3）——屈曲
AnsysWorkbench工程应用之——结构非线性（上）：几何非线性（3）——屈曲本文可能是您能在网络上找到得有限元计算屈曲最详细最接地气得文章。
图惜原本计划将屈曲写入几何非线性一文，后来发现内容太多，所有拎出来单独做一个专题。
在屈曲计算中，特别是非线性屈曲计算中，很多初学者也和图惜一样，有很多疑问，此文将针对初学者常见的问题做通俗详细的解读，其中一定有您想要的答案。
1 屈曲的概念结构失稳即屈曲，最常见的便是压杆失稳现象。
压杆稳定示意图如下，在稳定点之前，支反力呈线性增长，逐渐达到一个极值，之后支反力降低，这个极值便是屈曲极限。
屈曲极限往往远小于材料的屈服强度，屈曲分析的目的在于找出结构的屈曲极限，分析出结构的安全载荷、或对结构进行相应优化设计提高屈曲极限。
分析屈曲有两类方法，一类是线性特征值屈曲，用于计算理想线性屈曲极限，一类是非线性分析，用于计算零件因初始缺陷、材料、几何、接触等引起的非线性屈曲，而非线性分析又分为前屈曲分析和后屈曲分析。
很多结构设计是以理想线性屈曲极限除以一个安全系数作为设计依据，但是如果要探究结构的实际屈曲极限，有必要进行非线性屈曲分析。
特征值模态只是结构的线性特征,是结构在受荷载情况下能量最小的变形模式，不是真实变形。
最终采用大变形方法计算得到的结果才是结构真正的破坏状态。
2 线性屈曲在Ansys Workbench中，进行线性屈曲分析的是特征值屈曲模块。
线性特征值屈曲分析通过提取线性系统的刚度矩阵的奇异特征值，以获得结构临界失稳载荷以及失稳模态。
线性特征值屈曲分析不考虑初始结构缺陷与非线性因素的影响，计算较快，计算精度不如非线性屈曲，特别是对于复杂模型。
但是计算的特征值对结构稳定性评价有一定帮助，例如，求解出密集排列的负载乘数，则表明该结构对初始缺陷敏感；求解出稀松排列的负载乘数，则表明该结构对初始缺陷不敏感。
需要强调的是，线性特征值屈曲计算得到的失稳模态变形结果，并不是真实结构失稳后的结构最大位移。
Ansys Workbench非线性分析 牛顿辛普森法过程
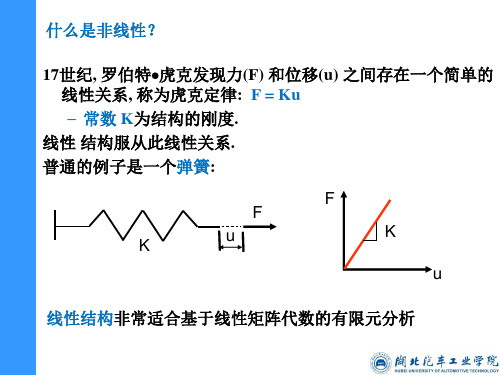
然而, 相当多的结构在力和位移之间没有线性关系 因为此类结构的 F-u 图不是直线, 这样的结构称为非线性结构 . – 刚度不再是一个常数K; 它成为施加载荷的函数, KT (切 线刚度). 普通的例子是韧性金属的拉伸试验:
载荷位移曲线
Fa Fnr
R
下一次迭代用刚度矩阵
u0 △ u u1
u0: 所设初始位移值
u
位移
KT :切向刚度
u1: 下次迭代位移值
R F a F nr
收敛： Newton-Raphson法需要一个收敛的度量以决定 何时结束迭代。给定节点Fa，节点力Fnr ，在一个体 中，节点载荷必须与节点力平衡
高级接触选项包括： 自动探测尺寸 Auto detection dimension and slider 非对称接触Asymmetric contact 接触结果工具Contact results tool 接触算法contact formulations Pinball 控制
膜片弹簧接触设置
带支撑环的膜片弹簧边界条件及求解设置
3 2 F1 269.991 2981 1 9238 1
膜片弹簧大端载荷-位移曲线
3 2 F1 269.991 2981 1 9238 1
注：膜片弹簧载荷挠度曲线为非线性，是由于大变形引起 的几何非线性，但材料始终发生的是弹性变形，没有发生 塑性变形
回忆材料力学中低碳钢力学性能试验
ANSYS求解非线性问题
ANSYS求解非线性问题牛顿一拉森方法ANS YS程序的方程求解器计算一系列的联立线性方程来预测工程系统的响应。
然而，非线性结构的行为不能直接用这样一系列的线性方程表示。
需要一系列的带校正的线性近似来求解非线性问题。
逐步递增载荷和平衡迭代一种近似的非线性救求解是将载荷分成一系列的载荷增量。
可以在几个载荷步内或者在一个载步的几个子步内施加载荷增量。
在每一个增量的求解完成后，继续进行下一个载荷增量之前程序调整刚度矩阵以反映结构刚度的非线性变化。
遗憾的是，纯粹的增量近似不可避免地随着每一个载荷增量积累误差，导种结果最终失去平衡，如图1所示所示。
（a）纯粹增量式解（b）全牛顿－拉普森迭代求解图1 纯粹增量近似与牛顿－拉普森近似的关系ANS YS程序通过使用牛顿－拉普森平衡迭代克服了这种困难，它迫使在每一个载荷增量的末端解达到平衡收敛（在某个容限范围内）。
图1（b）描述了在单自由度非线性分析中牛顿－拉普森平衡迭代的使用。
在每次求解前，NR方法估算出残差矢量，这个矢量是回复力（对应于单元应力的载荷）和所加载荷的差值。
程序然后使用非平衡载荷进行线性求解，且核查收敛性。
如果不满足收敛准则，重新估算非平衡载荷，修改刚度矩阵，获得新解。
持续这种迭代过程直到问题收敛。
ANS YS程序提供了一系列命令来增强问题的收敛性，如自适应下降，线性搜索，自动载荷步，及二分等，可被激活来加强问题的收敛性，如果不能得到收敛，那么程序或者继续计算下一个载荷前或者终止（依据你的指示）。
对某些物理意义上不稳定系统的非线性静态分析，如果你仅仅使用NR方法，正切刚度矩阵可能变为降秩短阵，导致严重的收敛问题。
这样的情况包括独立实体从固定表面分离的静态接触分析，结构或者完全崩溃或者“突然变成”另一个稳定形状的非线性弯曲问题。
10 ANSYS13.0 Workbench 结构非线性培训 作业 超弹曲线拟合
Workbench Mechanical – Structural Nonlinearities
…作业 6A – 超弹曲线拟合
Workshop Supplement
4. 对分别为excel 文件 ‘tension-eb.xls‟ 和 ‘tension-pt.xls‟的二轴试验数 据和剪力试验数据重复步骤 3的过程
…作业 6A – 超弹曲线拟合
Workshop Supplement
15. 选择如图的顶点，并插入用户定义结果对x向应力应变进行后处理
Vertex for user defined post processing
– x 向应力表示为 “SX” – x 向应变表示为 “EPELX”
– 用户定义结果语法参见 PRNSOL 帮助命令
Workshop Supplement
WS6A-5
Workbench Mechanical – Structural Nonlinearities
…作业 6A – 超弹曲线拟合
• 点击 ‘Return to Project‟ • 双击 Model 打开 FE模型(Mechanical Session) (或 RMB=>Edit…)
– Biaxial Test Data – Shear Test Data
Workshop Supplement
WS6A-9
Workbench Mechanical – Structural Nonlinearities
…作业 6A – 超弹曲线拟合
2. 熟悉属性表和图
2a Properties 对话框对超弹试验数据应包含三个额外组件 2b 属性表描绘的是2a中高亮显示的组件数据. 2c Engineering Data 制图是 2b中列表数据的图形显示.
ANSYS中的APDL命令总结
在ANSYS中，命令流是由一条条ANSYS的命令组成的一个命令组合，这些命令按照一定顺序排布，能够完成一定的ANSYS功能，这些功能一般来说通过菜单操作也能够实现（而那些命令流能够实现，菜单操作实现不了的单个命令比较少见）。
以下命令是结合我自身经验，和前辈们的一些经验而总结出来的，希望对大家有帮助。
（1）．Lsel, type, item, comp, vmin, vmax, vinc, kswp 选择线type: s 从全部线中选一组线r 从当前选中线中选一组线a 再选一部线附加给当前选中组aunoneu(unselect)inve: 反向选择item: line 线号loc 坐标length 线长comp: x,y,zkswp: 0 只选线1 选择线及相关关键点、节点和单元（2）．Nsel, type, item, comp, vmin, vmax, vinc, kabs 选择一组节点type: S: 选择一组新节点（缺省）R: 在当前组中再选择A: 再选一组附加于当前组U: 在当前组中不选一部分All: 恢复为选中所有None: 全不选Inve: 反向选择Stat: 显示当前选择状态Item: loc: 坐标node: 节点号Comp: 分量Vmin,vmax,vinc: ITEM范围Kabs: “0”使用正负号“1”仅用绝对值（3）．Esel, type, item, comp, vmin, vmax, vinc, kabs 选择一组单元type: S: 选择一组单元（缺省）R: 在当前组中再选一部分作为一组A: 为当前组附加单元U: 在当前组中不选一部分单元All: 选所有单元None: 全不选Inve: 反向选择当前组Stat: 显示当前选择状态Item：Elem: 单元号Type: 单元类型号Mat: 材料号Real: 实常数号Esys: 单元坐标系号（4）. mp, lab, mat, co, c1,…….c4 定义材料号及特性lab: 待定义的特性项目（ex,alpx,reft,prxy,nuxy,gxy,mu,dens）ex: 弹性模量nuxy: 小泊松比alpx: 热膨胀系数reft: 参考温度reft: 参考温度prxy: 主泊松比gxy: 剪切模量mu: 摩擦系数dens: 质量密度mat: 材料编号（缺省为当前材料号）c : 材料特性值，或材料之特性，温度曲线中的常数项c1-c4: 材料的特性-温度曲线中1次项，2次项，3次项，4次项的系数（5）. 定义DP材料：首先要定义EX和泊松比：MP，EX，MAT，……MP，NUXY，MAT，……定义DP材料单元表（这里不考虑温度）：TB，DP，MAT进入单元表并编辑添加单元表：TBDATA，1，CTBDATA，2，ψTBDATA，3，……如定义：EX=1E8，NUXY=0.3，C=27，ψ=45的命令如下：MP，EX，1，1E8MP，NUXY，1，0.3TB，DP，1TBDATA，1，27TBDATA，2，45这里要注意的是，在前处理的最初，要将角度单位转化到“度”，即命令：*afun,deg（6）. 根据需要耦合某些节点自由度cp, nset, lab,,node1,node2,……node17nset: 耦合组编号lab: ux,uy,uz,rotx,roty,rotz ,allnode1-node17: 待耦合的节点号。
Workbench DS非线性分析
[( ) ( ) ( )] ( ) σo =
1 2
σx −σ y 2 + σ y −σz 2 + σz −σx
2
+
6
τ2 xy
+τ
2 yz
+
τ
2 xz
ANSYS BASIC TRAINING
Mises 屈服准则
• 在主应力空间，von Mises 屈服面是圆柱面.
• 材料在屈服面内呈弹性弹性行为。注意，多轴应力状态可以存在于圆柱 面内的任何一点。在圆柱面边上会产生屈服。没有应力状态会存在于圆 柱面以外。硬化规则会描述圆柱面随响应的变化。
– 在绑定的接触中，纯粹的罚函数法可以想象为在接 触面间施加了十分大的刚度系数来阻止相对滑动。 这个结果是在接触面间的相对滑动可以忽略的情况 下得到的。
– MPC 方程当中对接触面间的相对运动定义了约束 方程，因此没有相互的滑动。这个方程经常作为罚 函数法的最好的替代。
ANSYS BASIC TRAINING
In this case, the gap between the two parts is bigger than the pinball region, so no automatic gap closure will be performed.
ANSYS BASIC TRAINING
载荷方向
Fb2
Fb1
Fa
Fa1
ANSYS BASIC TRAINING
xa
xb
非线性分析设置
• 非线性静力分析的过程与线性静力分析很相似，因此本节中不再详述各 个步骤。黄色斜体字的步骤包含了非线性分析中的特有选项。 – 导入几何模型 – 指定材料属性（如果需要：金属塑性） – 定义接触选项 （如果需要） – 定义网格控制 （可选择） – 施加载荷或约束 – 选择需要查看的结果 – 设置非线性选项 – 求解模型 – 查看结果
基于ANSYSWorkbench的悬臂梁结构非线性屈曲分析
三、根据 ASME 规范第Ⅲ卷附录 F 计算结构的临界载荷
为保证核电设备在事故工况下不发生损坏，ASME 规定用 D 级使用限制进行评定， 即用附录 F 进行评价。根据附录 F1334.3，轴向承压构件中的最大许用载荷应按下述(a) 或(b)加以限制。其中(a)包括两种方法，一是考虑大变形、实际受载状态变形、不直度及 其它公差等效应的综合稳定性分析；二是全尺寸原型实验。前者可借助有限元软件进行 分析，应用较广，后者因耗资巨大等原因极少采用。按照(a)确定的屈曲载荷的 2/3，作 为结构的最大许用载荷。(b)为公式法，工程上基本都采用该方法。下面利用该方法来计 算结构的最大许用载荷。 首先计算悬臂梁的长细比λ，其计算式为
(
Kl 1 ) R
Sy E
（1）
式中 K 为长度系数，对于悬臂梁，K 取 1；l 为结构无支撑长度；R 为梁的惯性半径， R= I / A ，其中 I、A 分别为梁截面惯性矩与截面积；Sy 为材料的屈服强度；E 为材料 的弹性模量。 将上述参数值代入上式中，即可求得：λ=2.495。可以看出，λ＞ 2 。根据附录 F1334.3(b)(1)，则结构的最大许用载荷计算式为
图 4 提取的带缺陷结构的有限元模型
V-313
2.5 非线性静力学分析 从图 1 所示的“Finite element modeler”模块导出“static structural(ANSYS)”模块， 并按住 “Finite element modeler” 模块下的 model 子模块， 拖放到 “static structural(ANSYS)” 的 model 子模块上。在本步中，添加的压力载荷值取线性屈曲预测的临界载荷，即 P=1.6106×107N；位移边界条件不变，左端固支。此外，large deflection 设置为 on，auto time stepping 设置为 on，maximum substeps 设置为 1.e+006。经过 11 次子步迭代，结果 收敛，得到最大的临界载荷 Pnlj=1.6105×107 N。
Ansys入门学习笔记
ANSYS Product LaucherCustomization/Preference>Graphic device name:图形显示卡设备设置。
在PC的操作环境下，一般设置为Win32，若显示支持OpenGL，则可选用3D。
Pick MenuLoop表示选择相连的对象Maximum表示最多可选的数量Minimum表示最少必选的数量以键盘输入数据的格式：如果是坐标位置，注意其所指的是WP Coordinates或Global Cartesian；如果是对象编号，则有两种形式，List of Items和Min,Max,IncANSYS文件系统ERR错误记录文件，LOG命令记录文件，DB数据库文件R开头的文件：RST结构分析的结果RTH热导分析的结果RMG电磁分析的结果其它如EMAT，ESA V，OSA V，TRI视其是否已完成阶段任务而决定清除与否ANSYS命令格式命令的输入是以自由字段方式输入的，因此不需要固定命令及其参数字段的大小以“/”打头的大部分是属于辅助功能性质的命令以“*”打头的大部分属于APDL（Ansys Parameter Design Languange）的命令当把需要的命令整合放在一个ASCII码的文件中时，就形成了命令输入文件。
命令输入文件没有特定对文件名及扩展名的要求，只是不要使用中文。
应力和应变（stress和strain）：（1）Nodal Solution：会将数据在节点的地方做平均（Average）处理，所画出来的应力图或应变图其数据是连续的。
（2）Element Solution：不会做平均，因此数据在元素和元素之间会呈现不连续的情况这两种数据显示方式是以等高线图的方式利用不同的颜色作为分隔显示出来，Ansys中称此种方式为Contour Plot。
一般来说，都是以Nodal Solution为准，但是比较两种方式所显示出来的数据，可帮助判断分析结果是否正确。
AnsysWorkbench工程应用之——结构非线性（序）：概述
AnsysWorkbench工程应用之——结构非线性（序）：概述各位道友，在时隔半年后，我又回来了，虽然由于水平有限，我依然无法给各位答疑解惑，但是我可以和大家一起学习学习一下基本理论知识。
从本文开始，图惜和大家开始共同学习结构非线性。
本文作为非线性知识的序篇，我们主要通过以下问题来学习结构非线性基本概念：问题1：什么是非线性？问题2：非线性的类型？1 什么是非线性前面介绍的许多内容都是结构线性问题，即满足胡克定律其中刚度矩阵[K]是一个常量，通俗地说，如果力F增大一倍，位移u也将增大一倍。
然而，实际工程中很多结构的力和位移的关系不呈线性关系，称之为非线性结构。
结构刚度不再是常数，而是随着载荷的变化而发生变化。
KT（切向刚度）代表了经过载荷位移曲线上的某一点，该曲线切线的斜率。
非线性问题分为三类，三类往往交叉出现：1.几何非线性，如大应变、大挠度大转动、应力钢化、旋转软化等。
2.材料非线性，如弹塑性、超弹性、蠕变、黏弹性等。
3.状态非线性，也称为边界条件非线性，如接触、生死单元等。
#2 非线性分析基础2.1几何非线性物体受载荷后，内部会发生变形，当应变远小于1%时，可忽略物体前后变形的形状和位置，简化为线性分析。
但是当结构承受大变形时，变形的几何形状可能会引起结构非线性响应。
一般几何非线性有大应变，大挠度，应力钢化等，它们的关系如下在Ansys Workbench中，如果要使用几何非线性功能，只需要打开分析设置中的大变形选项：Large Deflection=On，程序将考虑大应变，大挠度，应力钢化、旋转软化等效应。
（1）大应变，结构刚度由网格单元刚度和方向决定，单元的形状发生变化，从而最终引起结构的非线性响应。
所有的几何非线性现象几乎最终都会导致网格单元的大应变。
有限应变也属于这一类型，例如金属冷作成型过程中的有限塑性变形。
值得注意的是，大应变不一定导致大应力，如橡胶、海绵的大变形大变形不一定导致大应力。
ansys命令流学习笔记-workbench中命令流的一些应用
ansys命令流学习笔记-workbench中命令流的一些应用!ANSYS命令流学习笔记5workbench中命令流的一些应用学习重点：1. 定义单元类型2. 使用各向异性材料时，定义其单元为圆柱坐标系3. 有角度吊装时，定义吊装约束4. workbench、APDL的联合仿真案例如下：如下图模型，四个顶点通过杆件连接，进行吊装时的有限元分析。
1. 建立模型，设定必要的坐标系。
分成两个solid，内部的圆柱，剩余的矩形部分。
建立两个坐标系，分别用于指定各向异性材料的属性、吊装的固定点。
下图，建立圆柱坐标系，编号100，用于指定各向异性材料。
下图，建立直角坐标系，编号12，用于指定吊装固定点。
2. 建立named selection，方便在命令流中选择必要的元素。
下图，将四个吊装点，中间的圆柱，分别定义为任何名称，必须是英文才能用于APDL 命令中。
3. 定义边界条件，施加重力加速度，在static structural 下插入command(APDL) ，内容如下/prep7allscmsel,s,c1,elem !选择c1单元所有节点,既圆柱体的所有单元emodif,all,esys,100 !其坐标系转换为100坐标系，因为缠绕的各向异性材料必须在圆柱坐标系下定义单元的坐标。
!完成对各向异性材料的坐标系设定。
et,10,10 !定义编号为10的，link10单元r,10,0.01 !定义编号为10的实常数0.01，用于定义link10单元的截面积0.01mm^2*get,nmax,node,,num,max !获取node的最大数值，储存在nmax名称的变量里csys,12 !调用csys12坐标系n,nmax+1, !csys坐标原点建立node，后面会将其固定，既吊装的固定点mat,1type,10 !选取编号10的单元类型real,10 !选取编号10的实常数cmsel,s,kk1,node !选择kk1点，kk1已经定义为named selection*get,k1,node,,num,max !获取已选节点中的节点数最大值，既kk1的节点编号，取值为k1cmsel,s,kk2,node ! k2,k3,k4方法类型k1*get,k2,node,,num,maxcmsel,s,kk3,node*get,k3,node,,num,maxcmsel,s,kk4,node*get,k4,node,,num,maxalls !全选e,nmax+1,k1e,nmax+1,k2e,nmax+1,k3e,nmax+1,k4 !建立四个link单元d,nmax+1,allalls/sol此外，下图中单位必须保持一致，不然计算很容易出问题。
APDL与命令流使用
最新经典 ANSYS 及 Workbench 教程 电子工业出版社
-6-
APDL 与命令流的使用
2）ANSYS 宏文件的定义方法： z 方法 1－参数的值不确定，参数名被写入文件中。
*CREATE，Fname，Ext，Dir …… *END z 方法 2－*CFOPEN，Fname，Ext，Dir，Loc …… *CFWRITE，Command z 方法 3－通过菜单创建：Utility Menu＞Macro＞Create Macro z 方法 4－通过文本编辑器进行编辑。这是最常用的方法 3）宏库的创建 宏库文件包含一批宏，用*CREATE 命令或文本编辑器创建。宏库文件没有明确文件扩展名。 宏库的典型格式如下： MACRONAME1 …… /EOF MACRONAME2 …… /EOF MACRONAME2 …… /EOF 下面是包括两个简单宏的宏库文件： mybloc /prep7 /view，，-1，-2，-3 block，，4，3，2 finish /EOF mysphere /prep7 /view，，-1，-2，-3 sphere，1 finish /EOF
-8-
APDL 与命令流的使用
以有自己的默认值，如图所示。 格式：*ASK，Par，Query，DVAL 功能：提示用户输入一个参数值对话框 值域：Par 参数名
Query 提示文字（最多 32 个字符） DAVAL 参数的默认值
5.2 多变量提示对话输入框
多变量提示对话输入框一次可以输入多个参数。如图 9 所示
APDL 与命令流的使用
z 赋值； z 批量数据处理（运算/读写）。 参数的特点： z 不必声明参数类型； z 使用未声明参数赋“极小值”（约为 2E-100）； z 无论整型还是实型都按双精度存储； z 数组参数必须先定义后使用。
Ansys Workbench中添加APDL扩展workbench功能
APDL 目前只能在Geometry,Contact，Environment 和Solution 下插入。
尚不能对Mesh 有何控制。
但我个人认为在V11 中，WB 的mesh 并不比Classic 的差。
在WB tree 的不同位置插入的APDL 跟在Classic 中相对应的环境如图所示在开始介绍前，有必要强调一下Named Selection ，因为这使得在APDL 中选上几何部分(点线面体)成为可能，而在APDL 中往往只对结构的一部分施加作用。
Named Selection 相当于Classic 中的CM 命令。
但在WB 中只会生成节点跟单元的集合。
到底是节点还是单元集合示情况而定。
比如Named Slection 是一个体，则肯定是单元集合。
Named Slection 是某个体上的一个面，则是节点集合，但是如果Named Slection 是壳结构上的一个面，则是单元集合。
在Geometry 和Contact 下插入APDL 是相对于Classic 中的/PREP7 环境。
我们在输入APDL 时可以不用以/PREP7 开头。
Enviornemnt 下的APDL 则对于/SOLU 环境。
如果我们需要/PREP7 下的命令，可以先转换，千万别忘了转回/SOLU 。
通常如下/PREP7 …… Fini /SOLU Solution 下的APDL 相对于/POST1 环境。
但也可以调用时间历程后处理。
但千万不能忘记转回/POST1 ，并确信是你所需要的荷载步。
比如/POST26 ... Fini /POST1 set,last 上面的最后一个命令也可以写成"set,near,,,0.1" 这个WB 就会给出时间为0.1 时的结果（如果已经存储的话）。
Geometry 下的APDL 在结构不同的部分下我们可以插入不同的APDL 。
而插入的APDL 只会对相对应的部分有影响。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
!ANSYS命令流学习笔记10-利用APDL在WorkBench中进行非线性屈曲分析
!学习重点：
!1、强化非线性屈曲知识
首先了解屈曲问题。
在理想化情况下,当F < Fcr时, 结构处于稳定平衡状态，若引入一个小的侧向扰动力，然后卸载, 结构将返回到它的初始位置。
当F > Fcr时, 结构处于不稳定平衡状态, 任何扰动力将引起坍塌。
当F = Fcr时,结构处于中性平衡状态，把这个力定义为临界载荷。
在实际结构中, 几何缺陷的存在或力的扰动将决定载荷路径的方向。
在实际结构中, 很难达到临界载荷，因为扰动和非线性行为, 低于临界载荷时结构通常变得不稳定。
要理解非线性屈曲分析，首先要了解特征值屈曲。
特征值屈曲分析预测一个理想线弹性结构的理论屈曲强度，缺陷和非线性行为阻止大多数实际结构达到理想的弹性屈曲强度，特征值屈曲一般产生非保守解, 使用时应谨慎。
!理论解，根据Euler公式。
其中μ取决于固定方式。
F cr=π2EI (μL)2
!有限元方法，
已知在特征值屈曲问题：
det([K e]+λ[K e(σ0)])=0
求解λ，即可得到临界载荷{F cr}=λ{P0}
而非线性屈曲问题：
([K e]+[K e(σ0)]){δ}={F}
其中[K e]为结构初始刚度，[K e(σ0)]为有缺陷的结构刚度，{δ}为位移矩阵，{F}为载荷矩阵。
非线性屈曲分析时考虑结构平衡受扰动（初始缺陷、载荷扰动）的非线性静力分析，该分析时一直加载到结构极限承载状态的全过程分析，分析中可以综合考虑材料塑性、几何非线性、接触、大变形。
非线性屈曲比特征值屈曲更精确，因此推荐用于设计或结构的评价。
!2、熟悉WB中非线性屈曲分析流程
(1) 前处理，施加单元载荷，进行预应力静力分析。
(2) 基于预应力静力分析，指定分析类型为特征值屈曲分析，完成特征值屈曲分析。
(3) 在APDL模块将一阶特征屈曲模态位移乘以适当系数，将此变形后的形状当做非线性分析的初始模型。
(4) 在FE modeler模块，读取APDL处理后的cdb文件数据，即变形后的有限元模型。
(5) 在新建的静力分析中施加载荷和约束。
所施加的载荷应比预测值高10%一21%。
(6) 定义载荷步选项，设置收敛算法。
(7) 求解，查看位移-载荷曲线结果。
!3、熟悉WorkBench与APDL之间的数据转换方式
(1) 结果文件转换，db文件输出到APDL（见笔记5）。
(2) 模型文件转换，FE model中db文件转换成cdb文件，只保留有限元模型。
!问题描述
!钢结构之间，在集中载荷P作用下的非线性屈曲分析，工作载荷0.5MPa。
!分析步骤：
(1) 进行特征值屈曲分析，结果如下，临界载荷14.82*0.5 = 7.4 MPa。
(2) 建立inp文件，写入命令如下图，保存文件。
放大系数较大，方便查看模型变形。
(3) 导出特征值分析结果到新的APDL模块，并在新建的APDL模块中导入上一步中的inp文件，在solution处右键单击，点击update（一般生产新模块都会update一下，不再赘述）；双击进入APDL模块，可以发现文件已导入。
(4) 将APDL生产的cdb文件导入到FE modeler模块，并双击进入FE modeler生产模型。
(5) 将FE modeler模块拖到新建的静力分析D2：model中。
Update。
进入求解，设置边界条件，求解条件。
(6) 查看位移-时间曲线，发现在0.468s，位移突然增加，判定此时发生屈曲。
载荷为ramped，所以此时载荷为0.468*15=7MPa。
即非线性屈曲结果为7MPa，比特征值分析结果稍小。