完整版工程问题与配套问题练习
人教版七年级数学上册产品配套问题和工程问题同步练习题

第三章一元一次方程3.4 实际问题与一元一次方程第1课时产品配套问题和工程问题用一元一次方程解决配套问题1.某土建工程共需动用15台挖运机械,每台机械每小时能挖土3 m3或者运土2 m3,为了使挖土和运土工作同时结束,安排了x台机械运土,这里x应满足的方程是( )A.2x=3(15-x)B.3x=2(15-x)C.15-2x=3xD.3x-2x=152.甲队有27人,乙队有19人共同完成一项工作.由于工作时间需提前,现从其他队抽调20人支援,使甲队人数是乙队人数的2倍,应调往甲队_____人,乙队_____人.3.加工某种产品需要两个工序,第一道工序每人每天可完成900件,第二道工序每人每天可完成1 200件.现有7位工人参加这两道工序,应怎样安排人力,才能使每天第一、第二道工序所完成的件数相等?4.红光服装厂要生产某种型号学生服一批,已知每3米长的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600米长的这种布料生产学生服,应分别用多少布料生产上衣和裤子,才能使上衣和裤子恰好配套?共能生产多少套?5.某家具厂生产一种方桌,1立方米的木材可做50个桌面或300条桌腿,现有10立方米的木材,怎样分配生产桌面和桌腿使用的木材,才能使桌面、桌腿刚好配套,共可生产多少张方桌?(一张方桌有1个桌面,4条桌腿)用一元一次方程解决工程问题1.加工1 500个零件,甲单独做需要12小时,乙单独做需要15小时,若两人合做x 小时可以完工,依题意可列方程为( )2.某工程由甲、乙两队单独施工分别需要3小时和5小时,若两队合做这项工程的80%,需______小时.11 1 500 1 500A.()x 1 500 B.()x 1 50012151215+=+=1 1 500 1 500 1 500C.()x 1 500 D.()x 112151215+=+=3.一项工作,甲独做需18天,乙独做需24天,如果两人合做8天后,余下的工作再由甲独做x天完成,那么所列方程为_______.4.甲车由A城到B城需4小时,乙车由B城到A城需6小时,若两车同时出发,相向而行,多少小时在中途相遇?5.一项工作,由1人做要40小时完成,现计划由2人先做4小时,剩下的工作要8小时完成,问还需增加几人?(假定每个人的工作效率都相同)参考答案用一元一次方程解决配套问题1、【解析】选A.安排x台机械运土,则安排(15-x)台机械挖土,故共挖土3(15-x) m3,运土2x m3,故所列方程为2x=3(15-x).2、【解析】设调往甲队x人,则调往乙队(20-x)人.根据题意,得:27+x=2(19+20-x),解得x=17,所以20-x=20-17=3.答案:17 33、【解析】设应安排x 人在第一道工序,则安排(7-x)人在第二道工序.根据题意,得:900x=1 200(7-x),解得:x=4,所以7-x=3.答:应安排4人在第一道工序,安排3人在第二道工序.4、【解析】设用x 米布料生产上衣,根据题意得解得x=360.600-x=600-360=240,答:用360米布料生产上衣,用240米布料生产裤子,共能生产240套. 5、【解析】设用x 立方米的木材做桌面,则用(10-x)立方米的木材做桌腿.根据题意,得4×50x=300(10-x),解得,x=6,所以10-x=4,可做方桌为50×6=300(张).答:用6立方米的木材做桌面,4立方米的木材做桌腿,可做300张方桌.x 600x23,33-⨯=⨯用一元一次方程解决工程问题1、关注数学的解题过程数学是一门非常严谨的科目,在平时的学习中,同学们应该养成积极思考、重视细节、严谨计算、活学活用的好习惯,这是学好数学的前提高效学习经验——注重解答过程中考状元XX在中考中仅仅丢掉了6分。
产品配套问题和工程问题练习题(课前小测含答案)

产品配套问题和工程问题
1.挖一条1210m的水渠,由甲、乙两队从两头同时施工,甲队每天挖130m,乙队每天挖90m,需几天才能挖好?设需用x天才能挖好,则下列方程正确的是( )
A.130x+90x=1210
B.130+90x=1210
C.130x+90=1210
D.(130-90)x=1210
2.甲、乙两个工程队合作完成一项工程,甲队一个月可以完成总工程的,乙队的工效是甲队的2倍.两队合作多长时间后,可以完成总工程的?
3.有33名学生参加社会实践劳动,做一种配套儿童玩具.已知每个学生平均每小时可以做甲元件8个或乙元件3个或丙元件3个,而2个甲元件,1个乙元件和1个丙元件正好配成一套.问应该安排做甲、乙、丙三种元件的学生各多少名,才能使生产的三种元件正好配套?
第1课时 产品配套问题和工程问题
1.A
2.解:设两队合作x 个月后,可以完成总工程的12.由题意得112x +212x =12
,解得x =2. 答:两队合作2个月后,可以完成总工程的12
. 3.解:设安排x 名学生做丙元件,则x 名学生做乙元件,(33-2x)名学生做甲元件.由题意得8(33-2x)=2×3x ,解得x =12,所以33-2x =9.
答:应该安排9名学生做甲元件,12名学生做乙元件,12名学生做丙元件,才能使生产的三种元件正好配套.。
工程问题 调配问题、配套问题

1、某工厂第一车间比第二车间人数的
54少30人,如果从第二车间调出10人到第一车间去,则第一车间人数是第二车间人数的43,这两个车间原来各有多少人?
2、某工厂有甲、乙、丙三个车间,分别有工人55人、45人、30人,现各车间按相同比例裁减工人,最后留下104人,求裁减后乙车间还有多少工人?
3、一项工程,甲单独做需要10天完成,乙单独做需要15天完成,两人合作4天后,剩下的部分由乙单独做,乙还需要几天完成?
7、某地为了打造风光地带,将一段长为360m的河道整治任务由甲、乙两个工程队先后接力完成,共用时20天,已知甲工程队每天整治24m,乙工程队每天整治16m,求甲、乙两队工程队分别整治了多长的河道。
8、某糕点厂中秋节前要制作一批盒装月饼,每盒中装2块大月饼和4块小月饼。
制作1块大月饼要用0.05kg面粉,1块小月饼要用0.02kg面粉,现在共有面粉4500kg,制作这两种月饼应各用多少面粉,才能生产最多的盒装月饼?。
复习 工程问题与配套问题

(3)一件工作,甲单独做20小时完成,乙单独 做12小时完成,丙单独做15小时完成,若先 由甲、丙合做5小时,然后由甲、乙合做,问 还需几小时完成?
人均效率 前一部分 工作 后一部分 工作 时间 5 工作量
1 1 20 15 1 1 20 12
x
1 1 ( )5 20 15 1 1 ( )x 20 12
产品类型 大齿轮 小齿轮
每人每天平 生产人 均产量 数 16 x 10 85-x
3×大齿轮=2×小齿轮 3×16x=2×10(85-x)
总产量 16x 10(85-x)
2.我市某服装厂要生产一批学生校服,已知每3米的 布可做上衣2件或裤子3条,因裤子旧得快,要求一件 上衣和两条裤子配一套,现计划用1008m的布料加工 成学生校服,应如何安排布料加工上衣和裤子才刚好 配套?
1 80 1 80
2
x
x+5
3 4
8
2x 80 8 ( x 5) 80
前一部分+后一部分=
2x 8 3 ( x 5) 80 80 4
1 6. 某车间加工一批零件,第一天完成了总量的 多 2 3
2
件,第二天完成了剩下的 1 少1件,这时还剩下38件没 有完成,这批零件共有多少件?
完成的量 第一天 第二天
人均效率 甲 乙 人数 工作量 获利
5 4
5x 16×5x 16-x 4(16- x) 24×4(16-x)
x
甲获利+乙获利=1440
16×5x+24×4(16-x)=1440
练习1:一件工作,甲单独做20h完成,乙 单独做12h完成.根据题意回答下列问题:
(1)若甲乙合做,需几小时完成这件工作? (2)若甲先单独做4h,剩下的部分由甲、乙合做, 还需几小时完成? (3)若甲乙先合作3h,由于乙有事先离开不做 了,剩下的由甲完成,还需要几小时完成? (4)若甲先做5h后,乙单独做了3h,剩下的由 甲乙合作,还需要几小时完成?
一元一次方程—配套问题与工程问题

(1)3(x-2)=2-5(x-2) (2) 2(x+3)-5(1-x)=3(x -1)(3)35.012.02=+--x x (4) 223146x x +--=(5)124362x x x -+--=(6) 112[(1)](1)223x x x --=-2 .有两个工程队,甲工程队有32人,乙工程队有28人,如果是甲工程队的人数是工程队人数的2倍,需从乙工程队抽调多少人到甲工程队?3.某厂一车间有64人,二车间有56人。
现因工作需要,要求第一车间人数是第二车间人数的一半。
问需从第一车间调多少人到第二车间?4.某车间有28名工人生产甲、乙两种零件,每人每天平均可生产甲种零件12个或乙种零件18个,要使生产的甲乙两种零件按1:2配套组装,问:生产两种零件的工人应该如何安排?5.某车间有51名工人,每名工人每天能加工甲零件16个,或加工乙零件21个。
现该车间准备完成一个轿车零件的订单,一辆轿车需要5个甲零件和3个乙零件配成一套,为了每天能配套生产,应如何安排工人?6、做某件工作,甲单独做要8小时才能完成,乙单独做要12小时才能完成,问:①甲做1小时完成全部工作量的几分之几?②乙做1小时完成全部工作量的几分之几?③甲、乙合做1小时完成全部工作量的几分之几?④甲做x小时完成全部工作量的几分之几?⑤甲、乙合做x小时完成全部工作量的几分之几?⑥甲先做2小时完成全部工作量的几分之几?乙后做3小时完成全部工作量的几分之几?甲、乙再合做x小时完成全部工作量的几分之几?三次共完成全部工作量的几分之几?结果完成了工作,则可列出方程:7、一项工程,甲单独做要10天完成,乙单独做要15天完成,两人合做4天后,剩下的部分由乙单独做,还需要几天完成?8.将一批工业最新动态信息输入管理储存网络,甲独做需6小时,乙独做需4小时,甲先做30分钟,然后甲、乙一起做,则甲、乙一起做还需多少小时才能完成工作?9.食堂存煤若干吨,原来每天烧煤4吨,用去15吨后,改进设备,耗煤量改为原来的一半,结果多烧了10天,求原存煤量.10.一水池有一个进水管,4小时可以注满空池,池底有一个出水管,6小时可以放完满池的水.如果两水管同时打开,那么经过几小时可把空水池灌满?11.一个水池安有甲乙丙三个水管,甲单独开12h注满水池,乙单独开8h注满,丙单独开24h可排掉满池的水,如果三管同开,多少小时后刚好把水池注满水?。
初中数学配套问题与工程问题习题

初中数学配套问题与工程问题习题1. 中国古代问题:有甲、乙两个牧童,甲对乙说:“把你的羊给我一只,我的羊数就是你的羊数的2倍”.乙回答说:“最好还是把你的羊给我一只,我们羊数就一样了”.若设甲有x只羊,则下列方程正确的是()A.x+3=2(x−1)B.x+1=2(x−2)C.x+1=2(x−3)D.x−1=x+12+12. 某商场把一个双肩背书包按进价提高50%标价,然后再按八折出售,这样商场每卖出一个书包就可赢利8元.设每个双肩背书包的进价是x元,根据题意列一元一次方程,正确的是()A.(1+50%)x×80%−x=8B.50%x×80%−x=8C.(1+50%)x×80%=8D.(1+50%)x−x=83. 《易·系辞上》有“河出图,洛出书”之说,河图、洛书是中国古代流传下来的两幅神秘图案,蕴含了深奥的宇宙星象之理,被誉为“宇宙魔方”,是中华文化阴阳术数之源.河图的排列结构如图所示,一与六共宗居下,二与七为朋居上,三与八同道居左,四与九为友居右,五与十相守居中,其中白圈为阳数,黑点为阴数,若从阳数和阴数中各取一数,则其差的绝对值为5的概率为( )A.1 5B.625C.825D.254. 小芳每分钟打90∼100字,他10分钟至少能打多少字?下列说法正确的是()A.因为100×10=1000(字),所以他10分钟至少能打1000字B.因为95×10=950(字),所以他10分钟至少能打950字C.因为90×10=900(字),所以他10分钟至少能打900字D.以上说法都不对5. 某商场销售一种商品,第一个月将此商品的进价提高20%作为销售价,共获利1200元,第二个月商场搞促销活动,将商品的进价提高15%作为销售价,第二个月的销售量比第一个月增加80件,并且商场第二个月比第一个月多获利300元.设此商品的进价是x元,则可列方程________.6. 甲、乙两人做机械零件.甲每小时比乙多做6个,甲做90个所用的时间与乙做60个所用的时间相等.若设甲每小时做x个,则可列方程________.7. 某学校需要购买一批电脑,有两种方案如下:方案l:到商家直接购买,每台需要7000元;方案2:学校买零部件组装,每台需要6000元,另外需要支付安装费等其它费用合计3000元.学校添置________台电脑时,两种方案的费用相同.8. 服装厂要生产一批某型号学生服,已知每3米长的布料可做上衣2件或裤子3条,一件上衣和一条裤子为一套,计划用600米长的这种布料生产学生服,共能生产________套.9. 七中育才学校组织八年级学生参加社会实践活动,若单独租用35座客车若干辆,则刚好坐满;若单独租用55座客车,则可以少租一辆,且余45个空座位.求该校八年级学生参加社会实践活动的人数.已知35座客车的租金为每辆320元,55座客车的租金为每辆400元.根据租车资金不超过1500元的预算,学校决定同时租用这两种客车共4辆(可以坐不满).请你计算本次社会实践活动所需车辆的租金.10. 七年级春游分前队和后队前队以4千米每小时的速度先走4千米后,后队以每小时6千米的速度出发同时派出王明骑车以每小时10千米的速度赶到前队后又以同样的速度返回后队.(1)后队过多长时间追上前队?(2)王明从出发到回后队用了多长时间?11. 学校组织植树活动,已知在甲处植树的有6人,在乙处植树的有10人,在丙处植树的有8人,现调来若干人去支援,使在甲、乙、丙三处植树的总人数之比为2:3:4.设支援后在甲处植树的总人数有2x人.(1)根据信息填表:________-10 ________-8(2)已知支援丙处的人数是支援乙处的人数的2倍,求支援甲、乙、丙三处各有多少人?12. 一项工程,甲队单独完成需40天,乙队单独完成需50天,现甲队单独做4天后两队合作.(1)求甲、乙合作多少天才能把该工程完成;(2)在(1)的条件下,甲队每天的施工费用为2500元,乙队每天的施工费用为3000元,求完成此项工程需付给甲、乙两队共多少元.13. 在《二元一次方程组》这一章的复习课上,李老师让同学们根据下列条件探索还能求出哪些量.某电器公司计划用甲、乙两种汽车运送190台家电到农村销售,已知甲种汽车每辆可运送家电20台,乙种汽车每辆可运送家电30台,且规定每辆汽车按规定满载,一共用了8辆汽车运送.(1)佳佳同学根据题意列出了一个尚不完整的方程组{x +y =?,20x +30y =∗,请写出佳佳所列方程组中未知数x ,y 表示的意义:x 表示________,y 表示________,该方程组中“?”处的数应是________,“∗”处的数应是________;(2)音音同学的思路是设甲种汽车运送m 台家电,乙种汽车运送n 台家电.下面请你按照音音的思路列出方程组,并求甲种汽车的数量.14. 用正方形硬纸板做三棱柱盒子,每个盒子由3个长方形侧面和2个等边三角形底面组成,硬纸板用如图两种方法裁剪(裁剪后边角料不再利用).现有19张硬纸板,其中x 张硬纸板用方法一裁剪,其余硬纸板用方法二裁剪.(1)分别求裁剪出的侧面和底面的个数;(用含x 的代数式表示)(2)若裁剪出的侧面和底面恰好全部用完,问能做多少个盒子?15. 我国南方地区出现大暴雨,多地受灾.某帐篷厂接到在规定时间内加工1500万顶帐篷的任务.加工了300万顶帐篷后,厂家把工作效率提高到原来的1.5倍,于是提前4天完成任务.(1)求工厂原来每天加工多少万顶帐篷?(2)若该工厂的加工能力是每天能生产普通帐篷和保暖帐篷合计100万顶,已知每生产普通帐篷1万顶成本为50万元;每生产保暖帐篷1万顶成本为250万元.该工厂若想每天的生产成本不高于17000万元,则每天至少应加工多少顶普通帐篷?参考答案与试题解析初中数学配套问题与工程问题习题一、选择题(本题共计 4 小题,每题 3 分,共计12分)1.【答案】C【考点】由实际问题抽象出一元一次方程【解析】根据甲的话可得乙羊数的关系式,根据乙的话得到等量关系即可.【解答】解:∵甲对乙说:“把你的羊给我1只,我的羊数就是你的羊数的两倍”,∴设甲有x只羊,则乙有x+12+1只,∵乙回答说:“最好还是把你的羊给我1只,我们的羊数就一样了”,∴x+12+1+1=x−1,即x+1=2(x−3).故选C.2.【答案】A【考点】由实际问题抽象出一元一次方程【解析】首先根据题意表示出标价为(1+50%)x,再表示出售价为(1+50%)x×80%,然后利用售价-进价=利润即可得到方程.【解答】设每个双肩背书包的进价是x元,根据题意得:(1+50%)x×80%−x=8.3.【答案】A【考点】古典概型及其概率计算公式【解析】根据阳数为1,3,5,7,9;阴数为2,4,6,8,10,利用古典概型的概率求法求解.【解答】解:由图可知,阳数为1,3,5,7,9,阴数为2,4,6,8,10,从阳数和阴数中各取一数的所有组合共有5×5=25个,满足差的绝对值为5的有(1,6),(3,8),(5,10),(7,2),(9,4)共5个,则其差的绝对值为5的概率为p=525=15.故选A.4.【答案】C【考点】简单的工程问题【解析】小芳每分钟打90∼100字,也就是每分钟最少打90个字,最多打100个字,所以要求10分钟至少打字的个数应用数据90个,即用每分钟打字最少的数量90个乘10分钟即可求解。
一元一次方程解决问题专练:配套、工程问题

专练一:配套问题1.有一个加工茶杯的车间,平均每个工人每小时可以加工杯身12个,或者加工杯盖15个.1个杯身配1个杯盖,车间共有90人,则安排多少人加工杯身,才能使每小时加工的杯身和杯盖正好配套?2.某车间有26名工人,平均每人每天可以生产800个螺钉或1000个螺母,1个螺钉需要配2个螺母.为使每天生产的螺钉和螺母刚好配套,设安排x名工人生产螺钉,则可列方程为.3.用铝片制作听装饮料瓶,每张铝片可制作瓶身16个或制作瓶底43个,一个瓶身与两个瓶底配成一套.现有150张铝片,则用张铝片制作瓶身,张铝片制作瓶底可以正好制成配套的饮料瓶.4.一张方桌是由一个桌面和四条桌腿组成的,如果1立方米木料可制作方桌的桌面50个,或制作桌腿300条,现在要用5立方米木料制作方桌,请你设计一下,用多少木料制作桌面,用多少木料制作桌腿,恰好配成方桌多少张?5.服装厂计划生产一批某种型号的学生服装,已知每3米长的某种布料可做2件上衣或3条裤子,一件上衣和一条裤子为一套,现仓库内存有这样的布料600米,若全部用来做这种型号的学生服装,应分别用多少布料做上衣和裤子,才能恰好配套?6.一个车间加工轴杆和轴承,每人每天平均可以加工轴杆12根或轴承16个,1根轴杆与2个轴承为一套,该车间共有90人,应该怎样调配人力,才能使每天生产的轴承和轴杆正好配套?专练二:工程问题1.一项工作,甲单独做需要10小时完成,乙单独做需要15小时完成,那么甲每小时完成总工作量的,乙每小时完成总工作量的.若设甲、乙合作需要x小时完成,则可列方程为,解得x=.2.一项工程,甲队单独完成需要20天,乙队单独完成需要30天.若先由甲队单独做5天,剩下部分由甲、乙两队合作完成,则还需要的天数是()A.9B.10C.12D.153.一项工作,甲单独做需要15小时完成,乙单独做需要10小时完成.若甲先单独做9小时,后因甲有其他任务调离,余下的任务由乙单独完成,则乙还要多少小时才能完成?4.七年级(1)班芳华和虹霖在做室内值日时,芳华单独做需15分钟完成,虹霖单独做需9分钟完成,若芳华单独做3分钟后,虹霖才到,剩下的由两人共同完成,则还需要几分钟才能做完?若5分钟后要上课了,她们能在上课前做完吗?5.[2019·安徽] 为实施乡村振兴战略,解决某山区老百姓出行难的问题,当地政府决定修建一条高速公路.其中一段长为146米的山体隧道贯穿工程由甲、乙两个工程队负责施工.甲工程队独立工作2天后,乙工程队加入,两工程队又联合工作了1天,这3天共掘进26米.已知甲工程队每天比乙工程队多掘进2米,按此速度完成这项隧道贯穿工程,甲、乙两个工程队还需联合工作多少天?教师详解详析专练一:配套问题1.90-x12x15(90-x)12x=15(90-x)502.1000(26-x)=2×800x3.8664[解析] 设用x张铝片制作瓶身,则用(150-x)张铝片制作瓶底.根据题意,得2×16x=43(150-x),解得x=86.150-x=150-86=64.即用86张铝片制作瓶身,64张铝片制作瓶底,可以正好制成配套的饮料瓶.4.解:设用x立方米木料制作桌面,用(5-x)立方米木料制作桌腿,恰好配成方桌.根据题意,得4×50x=300(5-x),解得x=3.5-x=2,50x=150.因此,用3立方米木料制作桌面,用2立方米木料制作桌腿,恰好配成方桌150张.5.解:设用x米布料做上衣,则用(600-x)米布料做裤子.根据题意,得=,解得x=360.因此600-x=600-360=240.答:用360米布料做上衣,用240米布料做裤子,才能恰好配套.6.解:设安排x人加工轴杆,则安排(90-x)人加工轴承.根据题意,得12x×2=16(90-x),解得x=36.90-x=90-36=54.答:安排36人加工轴杆,54人加工轴承,才能使每天生产的轴承和轴杆正好配套.专练二:工程问题1.+=1 62.A[解析] 设甲、乙两队合作完成还需要的天数是x,根据题意,得×5++x=1,解得x=9.3.解:设乙还要x小时才能完成.根据题意,得×9+x=1,解得x=4.因此,乙还要4小时才能完成.4.解:设还需要x分钟才能做完.根据题意,得×3++x=1,解得x=4.5.即还需要4.5分钟才能做完.因为4.5<5,所以若5分钟后要上课了,她们能在上课前做完.5.解:设甲工程队每天掘进x米,则乙工程队每天掘进(x-2)米,由题意,得2x+(x+x-2)=26,解得x=7.所以乙工程队每天掘进7-2=5(米).=10(天).答:甲、乙两个工程队还需联合工作10天.。
配套问题和工程问题(1)
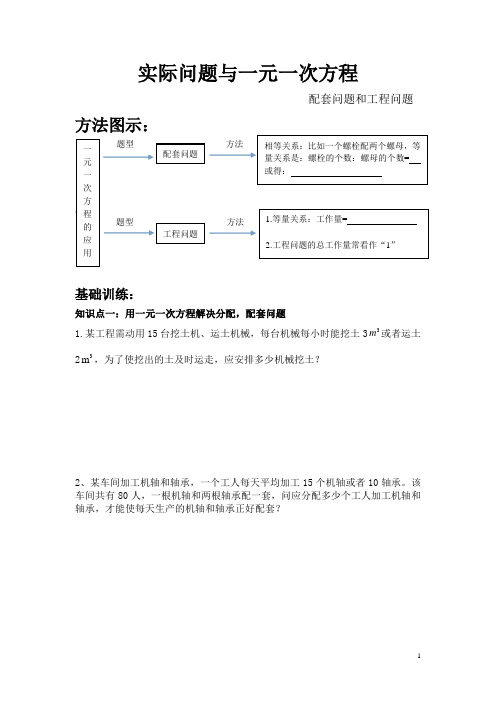
实际问题与一元一次方程配套问题和工程问题 方法图示: 题型 方法 题型 题型 方法基础训练:知识点一:用一元一次方程解决分配,配套问题1.某工程需动用15台挖土机、运土机械,每台机械每小时能挖土33m 或者运土23m ,为了使挖出的土及时运走,应安排多少机械挖土?2、某车间加工机轴和轴承,一个工人每天平均加工15个机轴或者10轴承。
该车间共有80人,一根机轴和两根轴承配一套,问应分配多少个工人加工机轴和轴承,才能使每天生产的机轴和轴承正好配套?一元一次方程的应用 配套问题 相等关系:比如一个螺栓配两个螺母,等量关系是:螺栓的个数:螺母的个数= 或得: 工程问题 1.等量关系:工作量= 2.工程问题的总工作量常看作“1”3、服装厂要生产某种型号的学生服装一批,已知3m 长的某种布料可做上衣2件或者裤子3条,一件上衣和一条裤子为一套,仓库存有这样的布料600m ,应分别用多少布料做上衣,多少布料做裤子才恰好配套?知识点二:用一元一次方程解决工程问题4.某班组每天需要生产50个零件才能在规定的时间内完成一项生产任务,实际上该班组每天比计划多生产6个零件,结果比规定的时间提前3天并超额生产了120个零件,求该班组完成零的数量。
5、整理一批图书,由1人做160小时完成,先由一些人做4个小时,再增加5人做6个小时,完成这项工作的43,问先安排了多少人做4个小时?(假设每个人的工作效率相同)6、某工人原计划用13个小时生产零件,后因每小时多生产10个零件,用12小时不仅完成了任务,还比原计划多生产了60个零件,问原计划生产多少个零件?综合演练7、包装厂有工人42人,每个工人平均每小时可以生产圆形钢铁片120片,或长方形铁片80片,将两张圆形铁片与一张长方形铁片可配套成一个密封圆桶,问如何安排工人生产圆形或者长方形铁片能合理的将铁片配套?8、某部队派出一支有25人组成的小分队参加防汛抗洪斗争,若每人每小时可装泥土18袋或每2人每小时可抬泥土14袋,如何安排人力,才能使装泥土和抬泥土密切配合,而刚好清场干净?9、在某班毕业晚会上,全班40名学生要用彩纸折纸鹤布置教室,但班里有10名同学因参加排练而没有参加,这样折纸鹤的同学平均每人折的数量比原定全班同学平均每人要完成的数量多5只,这个班共折了多少只纸鹤?10、某制衣厂接受一批服装订货任务,按计划天数进行生产,如果每天平均生产20套服装,就比订货任务少生产100套,如果每天生产23套服装,就可超过订货任务20套,问这批服装的订货任务有多少套?原计划多少天完成?11、学校有一批木料想做成课桌,一张课桌由一个桌面和四条桌腿组成,如果1立方米木料可制桌面50个或者制作桌腿300条,现有木料10立方米,请你帮助设计一下,用多少木料做桌子面,多少木料做桌腿,恰好配成多少张课桌?中考试炼12、整理一批图书,如果由一个人单独做要花60个小时。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1、一项工程,甲单独做要10天完成,乙单独做要15天完成,两人合做4天后,剩下的部分由乙
单独做,还需要几天完成?(要有“设、列、解、答”完整过程,下同)
2某工作,甲单独干需用15小时完成,乙单独干需用12小时完成,若甲先干1小时、乙又单
独干4小时,剩下的工作两人合作,问:再用几小时可全部完成任务?
3、某工程,甲单独完成续20天,乙单独完成续12天,甲乙合干6天后,再由乙继续完, 乙再做几天可以完成全部工程?
4、已知甲、乙二人合作一项工程,甲25天独立完成,乙20天独立完成,甲、乙二人合5天
后,甲另有事,乙再单独做几天才能完成?
5、一水池有一个进水管,4小时可以注满空池,池底有一个出水管,6小时可以放完满池的水, 如果
两水管同时打开,那么经过几小时可把空水池灌满?
1制作一张桌子要用一个桌面和 4条桌腿,1m 3木材可制作20个桌面,或者制作400条桌
腿,现有12m 3木材,应怎样计划用料才能使制作的桌面和桌腿配套?
解法指导:一个桌面配4条桌腿,即 ……丄十 _______________________ ,则可得等量关系为
桌腿总数量
解:
2、某机械厂加工车间有85名工人,平均每人每天加工16个大齿轮或10个小齿轮,已知2 个大齿轮与3个小齿轮配成一套,问需分别安排多少名工人加工大齿轮和小齿轮,才能使每 天加工的大小齿轮刚好配套?
解:
3、某校七年级2班共有56名学生,在一节科技活动课上制作长方形纸盒,已知每名同学一 节课可制作盒身20个或盒盖30个,一个盒身和两个盒盖配成一个长方形纸盒,为使一节课 制作的盒身、盒盖刚好配套,应安排制作盒身和盒盖的同学各多少名?
4、某车间每天能生产甲种零件120个,或者乙种零件100个。
甲、乙两种零件分别取3个、 2个才能配成一套。
要在30天内生产最多的成套产品,问怎样安排生产甲、乙两种零件的天 数?
【利润盈亏】问题
1、某商品标价是 750 元,商店打七折出售后,利润率为 5%,那么商品的进价是多少元?
解法指导:
2个大齿轮配3个小齿轮,即 大齿轮总数量 小齿轮总数量 _____ ,则等量关系为
大齿轮总数量 小齿轮总数量
2、某商品每件的进价是250 元,按标价的九折出售时,商品的利润率为15.2%,这种商品每件的标价是多少元?
3、某商品的进价是200 元,标价是300 元,打折销售时利润率为5%,那么该商品是按几折出售的?
4、一商店将每台彩电按进价提高40%,然后在广告上写“新年大酬宾,八折优惠” ,结果每台彩电盈利300 元,那么销售这种彩电的利润率是多少?
5、一家商店因换季准备将一种成本为120 元的服装打折销售,如果这种服装的原标价是200 元,为了保证不亏本,最多能打几折销售?
6、某商场举行周年庆,推出满200现金返160 购物劵,利用购物劵购物不再享受优惠。
问;张老师一共买回了1440 元的商品,实际上她最少花了多少钱?
7、一件衣服按成本提高50%标价,再以八折出售,结果获利28 元,这件衣服的成本是多少元?
8、某超市规定,如果购买的商品总额不超过50 元时,按全额收费:购买的商品总额超过50 元时,超过的部分按9 折收费。
某顾客在一次消费中向售货员缴纳了212 元,那么此次消费中该顾客购买的商品的价值是多少元?
9、为节约能源,某单位按以下规定收取每月电费:用电不超过140 度的,按每度0.43 元收费,如超过140度,超过部分按每度0.53 元收费。
某用户四月份的电费平均每度0.5 元,该用户应交的电费是多少元?。
