美国数学大联盟杯赛五年级试卷
美国“数学大联盟杯赛” 中国赛区 初赛五年级试卷

2017-2018年度美国“数学大联盟杯赛”(中国赛区)初赛(五年级)(初赛时间:2017年11月26日,考试时间90分钟,总分200分)学生诚信协议:考试期间,我确定没有就所涉及的问题或结论,与任何人、用任何方式交流或讨论, 我确定我所填写的答案均为我个人独立完成的成果,否则愿接受本次成绩无效的处罚。
请在装订线内签名表示你同意遵守以上规定。
考前注意事项:1. 本试卷是五年级试卷,请确保和你的参赛年级一致;2. 本试卷共4页(正反面都有试题),请检查是否有空白页,页数是否齐全;3. 请确保你已经拿到以下材料:本试卷(共4页,正反面都有试题)、答题卡、答题卡使用说明、英文词汇手册、 草稿纸。
考试完毕,请务必将英文词汇手册带回家,上面有如何查询初赛成绩、 及如何参加复赛的说明。
其他材料均不能带走,请留在原地。
选择题:每小题5分,答对加5分,答错不扣分,共200分,答案请填涂在答题卡上。
1. The smallest possible sum of two different prime numbers isA) 3B) 4C) 5D) 62. The greatest common factor of two numbers is3. The product of these two numbers mustbe divisible byA) 6 B) 9 C) 12 D) 18 3. The sum of 5 consecutive one-digit integers is at most A) 15 B) 25 C) 35 D) 45 4. How many two-digit multiples of 10 are also multiples of 12?A) 4B) 3C) 2D) 15. I have read exactly13of the total number of chapters in my 120-page book. If each chapter has the same whole number of pages, then the total number of chapters I have left could beA) 16 B) 24 C) 32 D) 50 6. What is the greatest odd factor of 44 × 55 × 66?A) 36 B) 55 C) 35 × 55 D) 36 × 55 7. What is the sum of the factors of the prime number 2017? A) 2016B) 2017C) 2018D) 20198. Lynn ran in 6 times as many races as the number of racesshe won. How many of her 126 races did Lynn not win?A) 21B) 90C) 96D) 1059. The least common multiple of 8 and 12 is the greatest common factor of 120 andA) 80B) 124C) 144D) 18010. January has the greatest possible number of Saturdays when January 1 occurs on any ofthe following days of the week exceptA) Thursday B) Friday C) Saturday D) Sunday 11. The number that is 10% of 1000 is 10 more than 10% ofA) 90B) 100C) 900D) 99012. The sum of 16 fours has the same value as the product of ? fours.A) 2 B) 3 C) 4 D) 16 13. Of the following, which is the sum of two consecutive integers?A) 111 111B) 222 222C) 444 444D) 888 88814. Abe drove for 2 hours at 30 km/hr. and for 3 hours at 50 km/hr. What was Abe’s averagespeed over the 5 hours?A) 35 km/hr.B) 40 km/hr.C) 42 km/hr.D) 45 km/hr.15. My broken watch runs twice as fast as it should. If my watch first broke at 6:15 P.M.,what time was displayed on my watch 65 minutes later?A) 7:20 P.M. B) 7:25 P.M.C) 8:20 P.M. D) 8:25 P.M.16. (2018 × 2017) + (2018 × 1) =A) 20172 B) 20182 C) 20183D) (2018 + 2017)217. A prized bird lays 2, 3, or 4 eggs each day. If the bird laid 17 eggs in 1 week,on at most how many days that week did the bird lay exactly 2 eggs?A) 2B) 3C) 4D) 518. Of the following, which could be the perimeter of a rectangle whoseside-lengths, in cm, are prime numbers?A) 10 cmB) 22 cmC) 34 cmD) 58 cm19. The average of all possible total values of a 4-coin stack of nickels and dimes (containingat least one of each coin) isA) 20¢B) 30¢C) 40¢D) 60¢20. The diameter of Ann’s drum i s 40 cm more than the radius. What is half the circumference of the drum?A) 120π cmB) 80π cmC) 60π cmD) 40π cm21. Of the following, which expression has the greatest number offactors that are multiples of 2018?A) 2018 × 12B) 20182C) 20192D) 20192019第1页,共4页 第2页,共4页22. When the sum of the factors of a prime number is divided by that prime number, theremainder isA) 0 B) 1 C) 2 D) 3 23. What is the sum of the digits of the greatest integer that has a square root less than 100? A) 18B) 36C) 99D) 10024. My favorite number has 6 different factors. If the product of all 6 factors is 123, what isthe sum of the factors of my favorite number?A) 24B) 28C) 32D) 3625. For how many different pairs of unequal positive integers less than 10 is the least commonmultiple of the numbers less than their product?A) 6B) 7C) 8D) 926. Exactly 12 of the students in my class have at least one brother, and 12 have at least onesister. If 13have no siblings, what fraction of the students in my class have at least onebrother and at least one sister?A) 16 B) 15 C) 14 D) 1327. Each day, Sal swims a lap 1 second faster than on the daybefore. If Sal swims a lap in 60 minutes on the 1st day, on what day does he swim a lap in 10% less time than the 1st day?A) 359th B) 360th C) 361st D) 362nd 28. 20172018 × 20172019 = 2017 ? × 20171009A) 1010B) 2010C) 3028D) 403829. Both arcs AB and AD are quarter circles of radius 5, figure on the right.Arc BCD is a semi-circle of radius 5. What is the area of the region ABCD ?A) 25 B) 10 + 5π C) 50D) 50 + 5π30. For every $5 I earn from my job, I save $2. For every $4 I save from my job, I am givenan additional $1 from my parents to add to my savings. How much must I earn in order to have $40 in savings?A) $160B) $120C) $100D) $8031. In the figure on the right, the side-length of the smaller squareis 4. The four arcs are four semi-circles. Each side of square ABCD is tangent to one of the semi-circles. The area of ABCD isA) 32B) 36C) 48D) 6432. A million is a large number, a “1” follo wed by 6 zeros. A googol is a large number, a “1”followed by one hundred zeros. A googolplex is a large number, a “1” followed by a googol of zeros. A googolplexian is a large number, a “1” fo llowed by a googolplex of zeros. A googolplexian isA) 10100 B) 1001010C) 100101010D) None of the above33. An integral triangle is a triangle with positive integral side-lengths and a positive area.Such a triangle can have a perimeter as small as 3. What is the next smallest possible perimeter of an integral triangle?A) 4B) 5C) 6D) 734. 2 liter of 2% fat milk + 3 liter of 3% fat milk = 5 liter of ? fat milkA) 2.5%B) 2.6%C) 5%D) 6%35. One day, a motorist came to a hill that was ten-mile drive up one side and a ten-mile drivedown the other. He drove up the hill at an average speed of 30 miles per hour. How fast will he have to drive down the other side to average 60 miles per hour for the entire 20-mile distance?A) 30 miles per hour B) 60 miles per hour C) 90 miles per hour D) None of the above 36. What is the weight of a fish if it weighs ten pounds plus half its weight?A) 10B) 15C) 20D) 2537. Without using pennies, how many different combinations of coins (nickels, dimes,quarters) will make 30 cents?A) 3B) 4C) 5D) 638. A man once bought a fine suit for which he paid $30 more than14of its price. How much did he pay for the suit? A) $30B) $35C) $40D) $4539. A father is five times as old as his son. In fifteen years he will be only twice as old. Howold is the father at present?A) 40B) 35C) 30D) 2540. It takes 30 minutes to completely fill a tank. If, however, a hole allows13of the water that is entering the tank to escape, how long will it then take to fill the tank?A) 40 B) 45 C) 60 D) 90第3页,共4页第4页,共4页。
2019年夏季数学大联盟4-5年级个人赛(Iindividual Part2)真题【决赛】

2019 Math League SuMmAmTHerLTEoAuGrUnEaPmReEnSSt
Math League Press, PO BPo.Ox 1. 7B,oTxe1n7a,flTye,nNaeflwy, JNeersweyJe0r7s6ey700-70607107-0U0S1A7
4 5 \July, 2019 – Grades &
#2-3. (Time Limit: 7 minutes) If 2 watermelons can be exchanged for 7 apples and 3 apples can be exchanged for 4 bananas, for how many bananas can 12 watermelons be exchanged?
Individual Questions – Part 2 of 2
Each question is worth 10 points. Calculators are PROHIBITED. #2-1. (Time Limit: 7 minutes) Different letters in the word “MathLeague” represent different digits.
Part 2 ANSWERS (Individual Questions)
五年级美国大联盟第一阶段-数论专题(含题目翻译解析)完整版
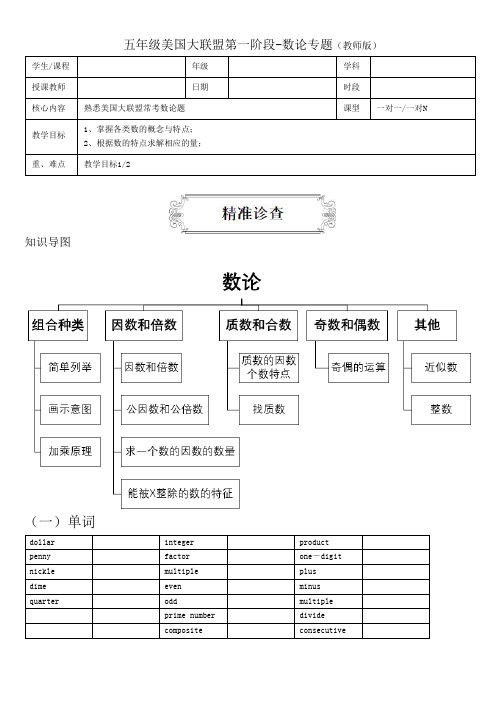
五年级美国大联盟第一阶段-数论专题(教师版)学生/课程年级学科授课教师日期时段核心内容熟悉美国大联盟常考数论题课型一对一/一对N教学目标1、掌握各类数的概念与特点;2、根据数的特点求解相应的量;重、难点教学目标1/2知识导图(一)单词dollar integer product penny factor one-digit nickle multiple plusdime even minus quarter odd multipleprime number dividecomposite consecutive(二)词组square root at least a millionpositive integers greatest common factor least common multiple two -digit multiples be divisible by the sum of【参考答案】square root 平方根 at least 至少 a million一百万 positive integers 正整数 greatest common factor 最大公因数 least common multiple 最小公倍数 two -digit multiples 两位数的倍数 be divisible by 被……整除 the sum of总和dollar 美元 integer 整数 product 积 penny 1美分 factor 因数 one -digit 一位数 nickle 5美分 multiple 倍数 plus 加 dime 10美分 even 偶数 minus 减 quarter25美分odd奇数 multiple 乘 prime number 质数 divide 除composite合数consecutive连续的导学一:组合种类知识点讲解1、简单列举有些题目,因其所求的答案有多种,用算式不容易表示,需要采用一一列举的方法解决。
五年级美国大联盟应用题专项(含题目翻译答案解析)
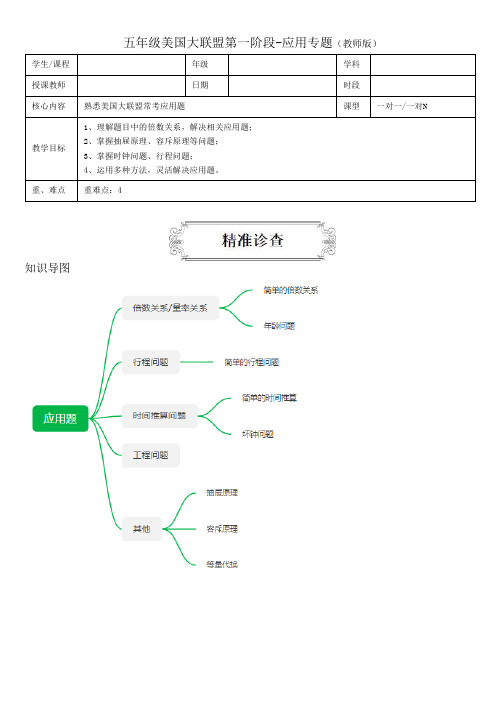
五年级美国大联盟第一阶段-应用专题(教师版)学生/课程年级学科授课教师日期时段核心内容熟悉美国大联盟常考应用题课型一对一/一对N教学目标1、理解题目中的倍数关系,解决相关应用题;2、掌握抽屉原理、容斥原理等问题;3、掌握时钟问题、行程问题;4、运用多种方法,灵活解决应用题。
重、难点重难点:4 知识导图导学一:倍数关系/量率关系知识点讲解1、简单的倍数关系(1)倍数问题小数(一倍数)×倍数=大数大数÷倍数=小数(一倍数)单位1×分率=对应量对应量÷分率=单位1(2)如何判断“一倍数”/“单位1”“的”前“比”后(3)解题方法①画图法:画线段图,用一格表示一倍数②方程法:设一倍数为X例题1.[单选题] [整数、小数复合应用题] [难度:★★★ ] Lynn ran in 6 times as many races as the number of races she won. How many of her 126 races did Lynn not win?A)21 B)90 C)96 D)105【参考答案】D【题目解析】翻译:Lynn参加的比赛是她赢的比赛的6倍,她126场比赛中有()场没有赢。
解析:Lynn参加的比赛是她赢的比赛的6倍,题目中“小数”为“赢的比赛”,求小数用除法:126÷6=21(场),没有赢的比赛:126-21=105(场)故选D。
2.[单选题] [列方程解含有一个量的应用题] [难度:★★★ ] What is the weight of a fish if it weighs ten pounds plus half its weight?A)10 B)15 C)20 D)25【参考答案】C【题目解析】翻译:如果一条鱼的重量是十磅加上它重量的一半,那么它的重量是多少? 解析:方法一:方程法。
解:设鱼的重量为X,则:X=10+X÷2,解得x=20方法二:算术法。
2014年美国“数学大联盟杯赛”(中国赛区)初赛五、六年级试卷

37. 将 1 ~ 9 九个数不重不漏地组成一个两位数、一个三位数、一个四位数。 这三个数均能被 9 整除,并且 7、8、9 分别在这三个数中,三个数十位 数字为三个连续的偶数,个位数字为三个连续的奇数。如果将四位数的 千位移到两位数的百位,组成新的三个三位数,新的三位数也均能被 9 整除。那么题中最初的三位数是 。 38. 如图为一个正方体有盖纸盒的示意图,在 1 ~ 30 的数中 选出 7 个,在纸盒的每个面填一个数。将盒盖的两个数 字相加后,三组相对面填的数均满足两两乘积相等。那 么 x 处的数字有 种可能。
姓名(签名)
A) 413 B) 1626 C) 21155 D) 161155 16. Which of the following figures has an odd number of sides? A) rhombus B) trapezoid C) pentagon D) hexagon 17. For how many integers from 55 to 66 is the ones digit greater than the tens digit? A) 4 B) 5 C) 10 D) 11 18. Lex buys 6 same-priced books and pays with a $50 bill. The change Lex receives is twice the price of a book. Each book costs A) $6.25 B) $7.14 C) $8.33 D) $12.50
14. If two consecutive whole numbers have a different number of digits, then their 一、选择题(每小题 5 分,答对加 5 分,答错不扣分,共 150 分,答案请填涂在答题卡上) 1. The band’s trombone plays 2013 notes, the trumpet plays 2014 notes, and the tuba plays 218 notes. That’s a total of ? notes. A) 6245 B) 6045 C) 4245 D) 645 2. The remainder when (999 999 999 + 666 666 + 333 + 1) is divided by 3 is A) 0 B) 1 C) 2 D) 3 3. 20 − 5 × 2 = 2 × ? A) 5 B) 15 C) 25 D) 30 C) 15 D) 100
2019年夏季数学大联盟4-5年级个人赛(Iindividual Part1)真题与解析【决赛】

Individual Questions – Part 1 of 2Each question is worth 10 points. Calculators are PROHIBITED.#1.(Time Limit: 7 minutes ) If six circles are tangent as shown, and each has an area of π, what is the area of the rectangle that just surrounds them, as shown?题目翻译: 如果6个面积为π的圆排列成图中的形状,那么图中的长方形的面积是多少?Solution:Since the area of each circle is π, each circle has a radius of 1 and a diameter of 2. The length across the rectangle consists of 3 diameters, and the width across the rectangle consists of 2 diameters. The dimensions of the rectangle are 6 by 4 and its area is 24.#2.(Time Limit: 7 minutes ) What is the least possible integer greater than 2019 that has remainder 11 when divided by 20 and 19?题目翻译: 请问大于2019的整数中满足除以20 和 19 都余11 的最小的数是多少?Solution:The least common multiple of 20 and 19 is 380, so we need an integer that is 11 more than amultiple of 380 and that is greater than 2019. Since 5 < 2019¸380 < 6, the least acceptable multiple is = 2280 and the number 11 more than this is 2291.#3. (Time Limit: 7 minutes ) I wrote each of the first 2019 positive integers in increasing order. Eachodd integer was written three consecutive times and each even integer was written two consecutive times. The first five integers I wrote were 1, 1, 1, 2, 2. What was the 2019th integer that I wrote?题目翻译:我把前2019个正整数按照从小到大的顺序写了出来。
2019年夏季数学大联盟4-5年级个人赛(Iindividual Part2)真题与解析【决赛】

Individual Questions – Part 2 of 2Each question is worth 10 points. Calculators are PROHIBITED.#2-1. (Time Limit: 7 minutes) Different letters in the word “MathLeague” represent different digits.What is the greatest possible value of the sum of the value of all 10 letters?题目翻译: MathLeague这个单词中的每一个不同的字母对应一个不同的数字(0...9这十个数字中的一个数字),请问这十个字母所对应的数字的和的最大值是多少?Solution:Since the letters “a” and “e” appear twice, let one of them have a value of 9 and the other onea value of 8. Each of the six other letters appears only once, so their values should be 7, 6, 5,4, 3, and 2. Assigning these values to the letters, the greatest possible sum is (18 + 16 + 7 + 6 +5 + 4 + 3 + 2) =61.#2-2. (Time Limit: 7 minutes) The number N = 2666666 . . . 666666 consists of a “2” followed by 2019 “6”s. What is the remainder when N is divided by 11?题目翻译: N = 266666…666666666,数字2后面有2019个6,N除以11的余数是多少?Solution 1:66 is a multiple of 11, so is any even number of 6 in a row. Let N1 = N–66…66 (2018 “6”s) =2600…00 (2018 “0”s). The remainder when N is divided by 11 is equal to the remainderwhen N1 is divided by 11.Let N2 = N1 – 2200...00 (2018 “0”s) = 400…00 (2018 “0”s). The remainder when N1 isdivided by 11 is equal to the remainder when N2 is divided by 11.Let N3 = N2 – 4 * 99…99 (2018 “9”s) = 4. Since 99…99 (2018 “9”s) is a multiple of 11, theremainder when N2 is divided by 11 is equal to the remainder when N3 is divided by 11. So the answer is4.Solution 2:There are 2020 digits in N. As we divide, we see that the quotient is 242424. . ., with the partial remainders after each step of the division alternating between 4 and 2. Since there are 2019 6s, the last remainder will be a4.#2-3. (Time Limit: 7 minutes) If 2 watermelons can be exchanged for 7 apples and 3 apples can be exchanged for 4 bananas, for how many bananas can 12 watermelons be exchanged?题目翻译: 如果2个西瓜可以换7个苹果,3个苹果可以换4个香蕉,那么12个西瓜可以换多少个香蕉?Solution:If 2 watermelons can be exchanged for 7 apples, 12 watermelons can be exchanged for 42 apples. Similarly, if 3 apples can be exchanged for 4 bananas, then 42 apples can be exchanged for56bananas.#2-4. (Time Limit: 7 minutes) Six years ago, Steve was six times as old as Rui. Six years from now, Steve will be 10 years older than Rui. How old is Rui?题目翻译: 6年前,Steve的年纪是Rui的年纪的6倍。
美国数学大联盟杯赛五年级试卷(2020新教材)

——教学资料参考参考范本——美国数学大联盟杯赛五年级试卷(2020新教材)______年______月______日____________________部门(初赛时间:2018年11月14日,考试时间90分钟,总分200分)学生诚信协议:考试期间,我确定没有就所涉及的问题或结论,与任何人、用任何方式交流或讨论,我确定以下的答案均为我个人独立完成的成果,否则愿接受本次成绩无效的处罚。
如果您同意遵守以上协议请在装订线内签名选择题:每小题5分,答对加5分,答错不扣分,共200分,答案请填涂在答题卡上。
1. A 6 by 6 square has the same area as a 4 by ? rectangle.A) 3 B) 6 C) 8 D) 92.Every prime has exactly ? positive divisors.A) 1 B) 2 C) 3 D) 4 or more3.If I answered 34 out of 40 questions on my math testcorrectly, I answered ? % of the questions correctly.A) 75 B) 80 C) 85 D) 904.120 ÷ 3 ÷ 4 × 12 =A) 1 B) 10 C) 12 D) 1205.10 × 20 × 30 × 40 = 24 × ?A) 1000 B) 10 000 C) 100 000 D) 1000 0006.One of my boxes contains 1 pencil and the others each contain 5 pencils. If there are101 pencils in my boxes, how many boxes do I have?A) 19 B) 20 C) 21 D) 227.of those are damaged. How many light bulbs are not damaged?A) 25 B) 504 C) 1512 D) 20xx8.50 × (16 + 24) is the square ofA) -40 B) -4 C) 4 D) 809.Which of the following numbers has exactly 3 positive divisors?A) 49 B) 56 C) 69 D) 10010.Ten people stand in a line. Counting from the left, Jerrystands at the 5th position. Counting from the right, which position is he at?A) 4 B) 5 C) 6 D) 711.On a teamwork project, Jack contributed 2/7 of the totalamount of work, Jill contributed 1/4 of the work, Patcontributed 1/5 of the work, and Matt contributed the rest.第1页,共4页Who contributed the most toward this project?A) Jack B) Jill C) Pat D) Matt12.Which of the following numbers is a factor of 20xx?A) 5 B) 11 C) 48 D) 9913.2 × 4 × 8 × 16 × 32 × 64 =A) 210B) 215C) 221D) 212014.On a game show, Al won four times as much as Bob, and Bobwon four times as much as Cy. If Al won $1536, how much did Al, Bob, and Cy win together?A) $96 B) $384 C) $1920 D) $20xx15. cannot beA) odd B) even C) 11 D) 1716.If a and b are positive integers such that a/b = 5/7, thena +b isA) 12 B) 24 C) 36 D) not able to be determined17.What is the greatest odd factor of the number of hours in all the days of the year 20xx?A) 3 B) 365 C) 1095 D) 328518. If the current month is February, what month will it be 1199 999 months from now?A) January B) February C) March D) April 19. ° less than the other. What is the measure of the larger angle?A) 36°B) 54°C) 63°D) 72°20. (The square root of 16) + (the cube root of 64) + (the 4throot of 256) =A) 12B) 24C) 32D) 6421. In ∆ABC, m ∠A – m ∠B = m ∠B – m ∠C. What is the degreemeasure of ∠B?A) 30B) 60C) 90D) 12022. For every 3 math books I bought, I bought 2 biology books. I bought 55 books in all. How many of those are math books?A) 11 B) 22C) 33D) 4423. ? 1s.A) 17B) 19C) 29D) 3224. Weird Town uses three types of currencies: Cons, Flegs, and Sels. If 3 Sels = 9 Cons and 2 Cons = 4 Flegs, then 5 Sels = ? Flegs.A) 12B) 24 C) 30 D) 3625. If the length of a rectangular prism with volume V isdoubled while the width and the height are halved, the volume of the new prism will beA) 4VB) V /2C) VD) 2V26. Rick and Roy each stands at different ends of a straight road that is 64 m long. They run toward each other. Rick ’s speed is 3 m/s and Roy ’s speed is 5 m/s. They will meet in? seconds.……………线…………………………………………………………… ……………答…………………题………………………………………。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
页脚内容- 2 -2015-2016年度美国“数学大联盟杯赛”(中国赛区)初赛(五年级)(初赛时间:2015年11月14日,考试时间90分钟,总分200分)学生诚信协议:考试期间,我确定没有就所涉及的问题或结论,与任何人、用任何方式交流或讨论, 我确定以下的答案均为我个人独立完成的成果,否则愿接受本次成绩无效的处罚。
如果您同意遵守以上协议请在装订线内签名选择题:每小题5分,答对加5分,答错不扣分,共200分,答案请填涂在答题卡上。
1. A 6 by 6 square has the same area as a 4 by ? rectangle.A) 3 B) 6 C) 8 D) 9 2. Every prime has exactly ? positive divisors.A) 1B) 2C) 3D) 4 or more3. If I answered 34 out of 40 questions on my math test correctly, I answered ? % of the questions correctly.A) 75B) 80C) 85D) 904. 120 ÷ 3 ÷ 4 × 12 =A) 1 B) 10 C) 12 D) 120 5. 10 × 20 × 30 × 40 = 24 × ?A) 1000B) 10 000C) 100 000D) 1000 0006. One of my boxes contains 1 pencil and the others each contain 5 pencils. If there are 101 pencils in my boxes, how many boxes do I have?A) 19B) 20C) 21D) 227. An electrical company imports 2016 light bulbs. Unfortunately, 25% of those are damaged. How many light bulbs are not damaged?A) 25 B) 504 C) 1512 D) 2016 8. 50 × (16 + 24) is the square ofA) -40 B) -4 C) 4 D) 80 9. Which of the following numbers has exactly 3 positive divisors?A) 49B) 56C) 69D) 10010. Ten people stand in a line. Counting from the left, Jerry stands at the 5th position. Counting from the right, which position is he at?A) 4 B) 5C) 6D) 711. On a teamwork project, Jack contributed 2/7 of the total amount of work, Jill contributed 1/4 of the work, Pat contributed 1/5 of the work, and Matt contributed the rest. Who contributed the most toward this project?A) Jack B) Jill C) Pat D) Matt 12. Which of the following numbers is a factor of 2016? A) 5 B) 11 C) 48 D) 99 13. 2 × 4 × 8 × 16 × 32 × 64 =A) 210B) 215C) 221D) 212014. On a game show, Al won four times as much as Bob, and Bob won four times as much as Cy. If Al won $1536, how much did Al, Bob, and Cy win together?A) $96 B) $384 C) $1920 D) $2016 15. The sum of two composites cannot beA) oddB) even C) 11 D) 1716. If a and b are positive integers such that a /b = 5/7, then a + b isA) 12B) 24C) 36D) not able tobedetermined 17. What is the greatest odd factor of the number of hours in all the days of the year 2015?A) 3 B) 365 C) 1095 D) 3285 18. If the current month is February, what month will it be 1 199 999 months from now? A) JanuaryB) FebruaryC) MarchD) April19. Two angles are complementary. One of these angles is 36° less than the other. What is the measure of the larger angle?A) 36° B) 54° C) 63° D) 72° 20. (The square root of 16) + (the cube root of 64) + (the 4th root of 256) = A) 12 B) 24 C) 32 D) 64 21. In ∆ABC , m ∠A – m ∠B = m ∠B – m ∠C . What is the degree measure of ∠B ?A) 30B) 60C) 90D) 12022. For every 3 math books I bought, I bought 2 biology books. I bought 55 books in all. How many of those are math books?A) 11B) 22C) 33D) 4423. John wrote a number whose digits consists entirely of 1s. This number was a composite number. His number could contain exactly ? 1s.A) 17B) 19C) 29D) 3224. Weird Town uses three types of currencies: Cons, Flegs, and Sels. If 3 Sels = 9 Cons and 2 Cons = 4 Flegs, then 5 Sels = ? Flegs.城市 区 准考证号 所在学校 年级 姓名(签名)………………………………………………装……………………………………………订……………………………………………线…………………………………………………………… ……………………………………装…………………订…………………线…………………内…………………不…………………答…………………题………………………………………第1页,共4页页脚内容- 2 -A) 12 B) 24 C) 30 D) 3625. If the length of a rectangular prism with volume V is doubled while the width and the height are halved, the volume of the new prism will beA) 4VB) V /2C) VD) 2V26. Rick and Roy each stands at different ends of a straight road that is 64 m long. They run toward each other. Rick ’s speed is 3 m/s and Roy ’s speed is 5 m/s. They will meet in ? seconds.A) 1B) 2C) 4D) 827. If the area of a certain circle is 2016, its radius isA) sqrt(2016/π) B) sqrt(4032/π) C) 2016/πD) 1008/π28. In a toy shop, the cost of a Teddy Bear is 200% as much as that of a toy train. The cost of a toy train is 6/5 the cost of a pack of the wooden blocks. The cost of a pack of wooden blocks is $50. What is the cost, in dollars, of the Teddy Bear?A) 60B) 100C) 120D) 20029. In the sequence 2016, 225, 141, 66, 432, 99, 1458 …, each term after the first term is the sum of the cubes of the digits of the previous term. What is the 100th term of this sequence?A) 153 B) 351 C) 370 D) 371 30. What is the sum of all the positive divisors of 210?A) 210 – 1B) 211 – 1C) 212 – 1D) 213 – 131. It takes 4 hours for Mike and Lucy to finish a task. It takes Lucy and Jerry 5 hours to finish the same task. And it takes 6 hours for Mike and Jerry to finish the same task. Lucy and Jerry first work on the task for 1 hour and 45 minutes. Then Mike takes over the task on his own. How many more hours does it take for Mike to finish the task?A) 3B) 4C) 5D) 632. If you sell a cloth at its current price, you get $40 profit. The total profit you get selling 10 clothes at 70% of its current price is equal to the total profit you get selling 20 clothes at $82 per cloth. What is the current price of a cloth?A) 80B) 100C) 120D) 12533. There are 6 identical squares in the figure on the right. The side length of each square is 1. Of all the triangles constructed by connecting three of the 18 vertices in the figure, how many of them are triangles whose area is 2 and which has at least one vertical or horizontal side?A) 12B) 16C) 24D) 2834. Pick up N numbers from 1 to 2015 inclusively, such that the sum of any three of the N numbers is divisible by 24. What is the maximum value of N ?A) 83 B) 84 C) 168 D) 25235. 汤姆有一件花了64美金买来的衬衫,他打算以比原价高出25%的价格出售,他会卖出多少钱?A) $16B) $32C) $48D) $8036. 满足以下条件的最小整数是多少:“除以3余2,除以5余4,除以7余6。
