人教版五年级下册《长方体和正方体》易错题整理
五下数学 长方体与正方体易错题训练 50题 带答案

长方体与正方体易错题训练50题1、一个正方体每个面的面积都是9平方厘米,这个正方体的棱长总和是(36)厘米。
2、一个长方体的长是5厘米,宽是3厘米,高是4厘米,它的表面积是(94 )平方厘米。
3、一个长方体不同方向三个面的面积分别是6平方厘米,12平方厘米,18平方厘米,则这个长方体的表面积是(72)平方厘米。
4、一个正方体的棱长是2厘米,把它的棱长扩大到原来的3倍,现在这个正方体的表面积是(216 )平方厘米。
5、正方体的棱长扩大到原来的3倍,表面积会扩大到原来的(9)倍。
6、把2个棱长3厘米的正方体拼成一个长方体,表面积比原来两个正方体减少( 18 )平方厘米,这个长方体的体积是( 54 )立方厘米。
7、把一根长80厘米,宽5厘米,高3厘米的长方体木料锯成长都是40厘米的两段,表面积比原来增加了(30)平方厘米。
8、一个长方体棱长之和是84厘米,长是8厘米,宽是7厘米,高是(6厘米),体积是(336 立方厘米)。
9、在括号里填上适当的数:4.3立方米=(4300)立方分米11.8立方分米=(11800)立方厘米3540立方厘米=(3.54 )立方分米6立方米40立方分米=(6.04)立方米5.5平方米=(5500)平方分米5立方分米180立方厘米=(5.18 )立方分米6.08升=(6)升(80)毫升2.4立方米=(2)立方米(400 )立方分米10、一个长方体的,长、宽、高都扩大到原来的2倍,它的表面积扩大到原来的(4)倍,它的体积扩大到原来的(8 )倍。
11、一个长8分米,宽0.7米,高5分米的长方体盒子,最多能够装下(24)个棱长为2分米的正方体木块。
12、一个长20厘米,宽20厘米,高15厘米的长方体纸盒内,最多能够放(700)个棱长为2厘米的正方体木块。
13、把3个棱长是4厘米的正方体木块粘合成一个长方体,这个长方体的体积是(192 )立方厘米,表面积比原来的3个小正方体表面积的和减少(64)平方厘米.14、将一个长为8分米宽为6分米,高为5分米的长方体木块切割成棱长为2分米的小正方体,一共可以割成(24 )块,把这些小正方体排成一行,一共长( 4.8 )米。
人教版五年级数学下册长方体和正方体重点易错题解析40例

人教版五年级数学下册长方体和正方体重点易错题解析(精选40例)【1】长方体的位置任意改变,体积不变。
(√)易错题解析:一个物体不论横着放、竖着放或还其他位置摆放,物体所占空间大小不变,即物体的体积和位置无关。
【2】有6个面,12条棱、8个顶点的物体就是长方体。
(×)错题解析:一个物体是长方体,必须中间的四条棱要垂直于上下底面,而有6个面,12条棱、8个顶点的物体有可能是6个面的斜棱柱,中间的四条棱与底面不垂直。
【3】长方体的三条棱分别叫做长方体的长、宽、高。
(×)错因解析:长方体相交于一个顶点处的三条棱分别叫做长方体的长、宽、高,而长方体中任意的三条棱有可能为三条相等的长(或宽,或高),也有可能有两条相等的长(或宽,或高)。
订正:长方体相交于一个顶点处的三条棱分别叫做长方体的长、宽、高。
【4】长方体的棱可以分成4组,每组3条棱,分别是长、宽、高。
(×)错因解析:长方体有12条棱,除相对的两个面都为正方形外,其中4条长,4条宽,4条高长度分别相等,因此长方体的棱可以分成3组,每组3条棱长度相等。
订正:长方体的棱可以分成3组,每组4条棱,分别是4条长、4条宽、4条高。
【5】在长方体中,只有相对的棱长度相等。
(×)错题解析:长方体中,长和宽、宽和高、长和高并不相对,但是当长方体相对两个面完全相同,如上、下面完全相同,此时长、宽、高三个数值中,有两个数值可能相等。
订正:在长方体中,不是相对的棱长度可能相等。
【6】一个长方体,不可能有8条棱的长度都相等。
(×)错题解析:在长方体中,周围的四个面是完全相同的长方形,此时如另一组相对的面是两个完全相同的正方形,此时这两个正方形的8条边长长度相等。
订正:一个长方体,可能有8条棱的长度都相等。
【7】长方体中最多有4个面完全相同。
(√)易错题解析:长方体相对的面如果是正方形,此时周围的四个面是形状和大小完全相同的长方形,如某些牙膏盒,某些装日光灯的包装盒,都是这样的长方体。
五年级下册数学长方体正方体易错题专项提升练习题附答案

五年级下册数学长方体正方体易错题专项提升练习题附答案一、易错题1、长、宽、高分别为30cm、30cm、20cm的小纸箱,在所有的棱上粘上一圈胶带,至少需要多长的胶带?2、五一劳动节,工人叔叔要在工人俱乐部的四周装上彩灯(地面的四边不装),已知工人俱乐部长90m,宽55m,高22m,工人叔叔至少需要多长的彩灯线?3、要做一个长2.2m、宽40cm、高80cm的玻璃柜台,现在要在柜台各边都安上角铁,至少需要多少米的角铁?4、一个长方体的饼干盒,长10cm,宽6cm,高12cm,如果围着它贴一圈商标纸(上、下面不贴),这张商标纸的面积至少有多少平方厘米?5、把一个棱长46cm的正方体纸箱的各面都贴上红纸,将它作为给希望小学捐款的"爱心箱"。
(1)他们至少需要多少平方厘米的红纸?(2)如果只在棱上粘贴胶带纸,一卷长4.5m的胶带纸够用吗?6、玻璃鱼缸的形状是正方体,棱长3dm,制作这个鱼缸时至少需要玻璃多少平方分米?(上面没有盖)7、一个长方体饼干盒,长18cm,宽12cm,高20 cm,现在要围着它贴一圈商标纸(上下两个面不贴),如果商标纸的接头处是3cm,那么这张商标纸的面积是多少平方厘米?8、做一件无底的长方体立式空调的布罩,地面是边长为4dm的正方形,高为17dm,至少要用多少布?9、一个长15厘米,宽12厘米,高8厘米的长方体玻璃容器,能装在一个长18厘米,宽14厘米,容积为1512立方厘米的的长方体盒子里吗?为什么?10、一个长20cm,宽10cm,高8cm的长方体容器,里面的水深5cm,把这个容器盖紧竖放后使长宽朝下,这时里面的水深多少厘米?11、爸爸买了一个长30cm,宽20cm,高15厘米的长方体礼盒,里面装有妈妈爱吃的长方形状的花生酥,每块花生酥长5cm,宽3cm,高2cm。
(1)若礼盒用彩纸包装,至少需要多少彩纸?(2)最多能装多少块花生酥?二、体积题类型一、较为复杂的求体积问题。
人教版五年级下册数学第三单元知识点易错点汇总(配练习完整版)[1]1
![人教版五年级下册数学第三单元知识点易错点汇总(配练习完整版)[1]1](https://img.taocdn.com/s3/m/4fd5c0207cd184254b3535f5.png)
人教版五年级下册数学第三单元知识点易错点汇总一、长方体和正方体的认识 【知识点1】要素 立体图形棱面 顶点数量 特征 数量 特征数量 特征长方体12互相平行的棱长度相等 6相对的面完全相同 8同一个顶点引出的三条棱分别叫做长、宽、高特殊长方体 12 垂直于正方形面的棱长度相等 6 两个面是正方形,其余四个面是完全相同的长方形 8正方体 12 所有的棱长度都相等6 所有面都是正方形且完全相同8一个长方体至少可以有两个面是正方形,最多可以有6各面是正方形,但不会存在3个、4个、5个面是正方形! 练习:(1)判断并改正:长方体的六个面一定是长方形; ( ) 正方体的六个面面积一定相等; ( )一个长方体(非正方体) 最多有四个面面积相等; ( )相交于一个顶点的三条棱相等的长方体一定是正方体。
( ) 一个长方体中,可能有4个面是正方形。
( ) 正方体是特殊的长方体。
( )长方体的三条棱分别叫做长、宽、高。
( )有两个面是正方形的长方体一定是正方体。
( ) 有三个面是正方形的长方体一定是正方体。
( ) 正方体的相邻三条棱的交点叫做顶点。
( )有两个相对的面是正方形的长方体,另外四个面的面积是相等的。
( ) 长方体和正方体最多可以看到3个面。
( )长方体的12条棱中,长、宽、高各有4条。
( )正方体不仅相对的面的面积相等,而且所有相邻的面的面积也都相等。
( ) 长方体(不包括正方体)除了相对的面相等,也可能有两个相邻的面相等。
( ) 一个长方体中最少有4条棱长度相等,最多有8条棱长度相等。
( ) (2)一个长方体最多有( )个面是正方形,最多有( )条棱长度相等。
(3)一个长方体的底面是一个正方形,则它的4个侧面是( )形。
(4)正方体不仅相对的面相等,而且所有相邻的面( ),它的六个面都是相等的( )形。
(5)把长方体放在桌面上,最多可以看到( )个面。
最少可以看到( )个面。
【知识点2】棱长和公式:长方体棱长和=(长+宽+高)×4 长+宽+高=棱长和÷4 长方体棱长和=下面周长×2+高×4 长方体棱长和=右面周长×2+长×4 长方体棱长和=前面周长×2+宽×4正方体棱长和=棱长×12 棱长=棱长和÷12 棱长和的变形:例如:有一个礼盒需要用彩带捆扎,捆扎效果如图,打结部分需要10厘米彩带,一共需要多长的彩带?分析:本题虽然并未直接提出求棱长和,但由于彩带的捆扎是和棱相互平行的,因此,在解决问题时首先确定每部分彩带与那条棱平行,从而间接去求棱长和。
五年级下册长方体、正方体易错及重难点题目
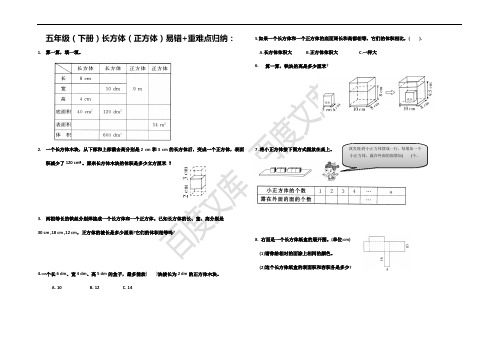
五年级(下册)长方体(正方体)易错+重难点归纳:1.算一算,填一填。
2.一个长方体木块,从下部和上部截去高分别是2 cm和3 cm的长方体后,变成一个正方体,表面积减少了120 cm²。
原来长方体木块的体积是多少立方厘米?3.两根等长的铁丝分别焊接成一个长方体和一个正方体。
已知长方体的长、宽、高分别是30 cm ,18 cm ,12 cm,正方体的棱长是多少厘米?它们的体积相等吗?4.一个长6 dm、宽4 dm、高5 dm的盒子,最多能放( )块棱长为2 dm的正方体木块。
A. 10B. 12C. 145.如果一个长方体和一个正方体的底面周长和高都相等,它们的体积相比,( ).A.长方体体积大B.正方体体积大C.一样大6.算一算,铁块的高是多少厘米?7 .将小正方体按下图方式摆放在桌上。
8. 右面是一个长方体纸盒的展开图。
(单位:cm)(1)请你给相对的面涂上相同的颜色。
(2)这个长方体纸盒的表面积和容积各是多少?我发现:将小正方体摆成一行,每增加一个小正方体,露在外面的面增加( )个。
9.一个底面长和宽都是2dm的长方体玻璃容器里面有5.6L水。
若将一个苹果浸没在水中,水深1.5dm,这个苹果的体积是多少立方分米?(玻璃厚度忽略不计)10. 观察量杯中水的变化,计算出大正方体的体积。
11 .右面玻璃容器的底面积是80cm²(不计玻璃厚度)。
观察图中变化,求大圆球的体积。
12.有甲、乙两个长方体水箱,甲水箱中水深35 cm,乙水箱中水深21cm。
现将甲水箱里的一部分水抽到乙水箱中,使两个水箱中的水面高度一样。
抽完水后两个水箱中的水深是多少厘米?(水箱厚度忽略不计) 13.一个长方体的玻璃缸长8 dm、宽6 dm、高4 dm,缸中水深2.8 dm。
如果放人一块棱长为4 dm的正方体铁块,缸里的水溢出多少升?14.下图是一个长方体容器,里面水深5.6 dm。
把一个南瓜放入(南瓜全部浸没在水中)后,从容器里溢出4L水。
长方体与正方体表面积易错点

长方体与正方体表面积易错点易错点1——概念不清,单位换算错误易错题(1)一个正方体的棱长总和是24厘米,它的表面积是()平方厘米;体积是()立方厘米。
【错误分析:第一种错误是把正方体的12条棱记成8条,;第二种错误是把表面积和体积混淆了。
】解答:24 8易错题(2)一个通风管长为5米,横截面是边长为100分米的正方形。
求做10根这样的通风管需要多少平方米的铁皮?错误答案:(5×100+100×100+5×100)×2=(500+10000+500)×2=22000(平方米)错误分析:没有统一单位,同时题目是要求10根通风管面积。
所以在做题时,首先观察单位不同,要注意统一单位。
看题目求的总量是几根的。
正确答案:100分米=10米(10×10+5×10+5×10)×2=200×2=400(平方米)400×10=4000(平方米)易错点2——没有根据实际情况来分析和解决,如计算无盖立方体的表面积时,要去掉没有的那个面。
易错题(1)一个鱼缸长为6cm,宽为4cm,高为2cm。
求鱼缸表面积。
错误答案:(6×4+4×2+6×2)×2=(24+8+12)×2=88(平方厘米)错误分析:鱼缸只有五个面,不能直接用表面积公式计算。
所以在计算鱼缸的表面积时只要算左右、前后以及下面这五个面的面积总和。
正确答案:(4×2+6×2)×2+6×4=(8+12)×2+24=64(平方厘米)易错点3——棱长、面积、体积的变化★说明:不管是长方体还是正方体的面积、体积变化都根据计算公式和积的变化规律进行判断。
棱长扩大n倍,棱长之和扩大n倍,表面积扩大n²倍,体积扩大n³倍。
易错题(1)长方体的长、宽、高同时都缩小3倍,它的表面积缩小()倍.A.3 B.9 C.6 D.27【根据长方体的表面积公式:s=(ab+ah+bh)×2,再根据因数与积的变化规律,积扩大或缩小的倍数等于因数扩大或缩小倍数的乘积】解答:B易错题(2)正方体的棱长扩大为原来的3倍,它的棱长之和、表面积和体积分别怎么变化?【①棱长之和的变化:根据正方体的棱长之和公式C=12a,可以判断一个因数12不变,另一个因数a扩大到原来的3倍,那么棱长之和也扩大为原来的3倍。
(易错题)最新人教版小学数学五年级下册第三单元长方体和正方体测试题(含答案解析)
(易错题)最新人教版小学数学五年级下册第三单元长方体和正方体测试题(含答案解析)一、选择题1.用一根52厘米的铁丝,恰好可以焊成一个长6厘米,宽4厘米,高()厘米的长方体框架。
A. 2B. 3C. 42.把一根横截面积是8平方厘米的长方体木料截成3段,表面积增加()A. 8平方厘米B. 16平方厘米C. 32平方厘米3.从8个棱长1cm的小正方体拼成的大正方体中,拿走一个小正方体(如图),这时它的表面积是()。
A. 18cm2B. 21cm2C. 24cm24.将三个棱长都是10厘米的正方体拼成一个长方体装在一起,此时与三个正方体独立包装相比,节省了()cm2的包装纸。
A. 100B. 400C. 6005.用长是72cm的铁丝做一个长方体框架,长是5cm,宽是4cm,高应是()。
A. 12cmB. 9cmC. 8cmD. 6cm6.用一根32cm长的铁丝做一个棱长是整厘米数的长方体框架,这个长方体框架的长、宽、高可能是()A. 7cm,2cm,1cmB. 5cm,2cm,1cmC. 5cm,3cm,2cmD. 3cm,2cm,1cm 7.下面图形()沿虚线不能折成正方体.A. B. C.8.一个长方体的集装箱,从里面测量长12m、宽4m、高3m,如果要装一批棱长2m的正方体货箱,最多能装()个.A. 12B. 18C. 369.要用()个棱长是1cm的小正方体才可以拼成一个棱长是3cm的大正方体.A. 9B. 18C. 27D. 54 10.正方体的棱长扩大到原数的3倍,表面积扩大到原数的()倍。
A. 3B. 9C. 611.一个长方体水箱,从里面量长5dm,宽和高都是2dm,现在往这个水箱早倒入20L水,水箱()。
A. 刚好满了B. 还没倒满C. 溢出水了12.一小瓶矿泉水的净含量是()。
A. 330LB. 330mLC. 330dm³二、填空题13.用一根长72cm的铁丝正好可以焊接成一个长9cm,宽8cm,高________cm的长方体。
人教版数学5年级下册 第3单元(长方体与正方体)易错题(附答案)
第3单元长方体和正方体易错题易错点大集合易错点一:基本认识典例如图,要拼成一个大正方体,至少还需要()个小正方体。
A.4B.3C.5跟踪训练1.图最多可以画出几个不同的长方形?()A.1个B.3个C.6个2.如果一个长方体有4个面的形状大小都相等,那么其余两个面一定是()A.正方形B.长方形C.长方形或正方形3.小芳用1立方厘米的小正方体摆成一个长方体,从正面和上面看到的是如右所示的图形。
这个长方体的棱长总和是()。
A.52厘米B.36厘米C.24厘米D.9厘米易错点二:棱长和典例用一根60cm长的铁丝,可以焊成长8cm,宽4cm,高( )cm长方体框架。
A.2B.3C.4D.5跟踪训练1.一个长方体的长、宽、高分别是5分米、4分米、6分米,棱长之和是()。
A.60分米B.60平方分米C.120立方分米2.用一根60厘米长的铁丝可以折成一个长8厘米、宽5厘米、高()厘米的长方体.()A.2B.3C.4D.53.一个正方体的棱长总和是60cm,它的棱长是()。
A.4cmB.5cmC.10cm易错点三:表面积典例将两个棱长为5cm的正方体拼成一个长方体,这个长方体的表面积是cm2。
跟踪训练1.一个正方体的棱长总和是96厘米,那么这个正方体的表面积是________平方厘米,2.把4个棱长为1cm的小正方体,拼成一个表面积尽可能小的长方体,其表面积为cm2。
3.(如图)把一个长方体平均分成两个正方体,正方体的棱长是3米,则原来长方体的表面积是________平方米,体积是________立方米。
易错点四:单位换算典例4升=________毫升6000毫升=________升8升60毫升=________毫升跟踪训练1.600平方分米=________平方米40毫升=________升2.07立方米=________立方米________立方分米2.在横线上填上适当的单位名称。
一块橡皮的体积大约是8一辆小汽车的油箱容积是30一个教室大约占地48小明每步的长度约是603.小明把1升牛奶倒入2个相同的杯中,每个杯子都倒满。
长方体和正方体易错题知识点整理
长方体和正方体易错题知识点整理
长方体和正方体易错题的知识点整理如下:
1. 边长与体积的关系:
- 长方体的体积等于底面积乘以高,公式为 V = lwh;
- 正方体的体积等于边长的立方,公式为 V = a^3。
2. 表面积的计算:
- 长方体的表面积等于底面积加上四个侧面的面积之和,公式为 S = 2lw + 2lh + 2wh;
- 正方体的表面积等于六个面的面积之和,公式为 S = 6a^2。
3. 对角线的长度:
- 长方体的对角线长度可以利用勾股定理计算,公式为 d =
√(l^2 + w^2 + h^2);
- 正方体的对角线长度等于边长的√3倍,公式为d = a√3。
4. 若给定长方体或正方体的体积或表面积,求边长或高度的计算:
- 长方体的长度、宽度、高度可以利用体积和底面积求解;
- 正方体的边长可以利用体积和表面积求解。
5. 若给定长方体或正方体的某一边长或高度,求体积或表面积的计算:
- 长方体的体积可以利用边长和底面积求解;
- 正方体的体积可以利用边长求解;
- 长方体的表面积可以利用边长和高度求解;
- 正方体的表面积可以利用边长求解。
6. 长方体和正方体之间的关系:
- 正方体是长方体的一种特例,即长方体的所有边长都相等。
这些知识点是长方体和正方体易错题常涉及的重点,建议反复巩固记忆和练习题目,加深理解和应用。
(易错题)最新人教版小学数学五年级下册第三单元长方体和正方体检测(含答案解析)(1)
(易错题)最新人教版小学数学五年级下册第三单元长方体和正方体检测(含答案解析)(1)一、选择题1.一个长6cm、宽4cm、高5cm的长方体盒子,最多能放()个棱长为2cm的正方体木块。
A. 14B. 13C. 122.一根正方体的木料,它的底面积是10cm2,把它截成3段,表面积增加了()cm2。
A. 20B. 40C. 60D. 803.学校要挖一个长40dm、宽20dm、深4dm的沙坑,需要()m3的黄沙才能填满。
A. 3200 B. 3.2 C. 324.用一根32cm长的铁丝做一个棱长是整厘米数的长方体框架,这个长方体框架的长、宽、高可能是()A. 7cm,2cm,1cmB. 5cm,2cm,1cmC. 5cm,3cm,2cmD. 3cm,2cm,1cm 5.如图,把这张硬纸片沿虚线折叠起来拼成一正方体,和3号相对的面是()号。
A. 2B. 4C. 5D. 66.下面的图形中,()能折成一个正方体。
A. B. C.7.一个长方体的长为7厘米,如果将长增加7厘米,宽和高不变,那么这个长方体的体积就扩大到原来的()倍。
A. 7倍B. 14倍C. 2倍8.至少需要()个同样的小正方体,才可以拼成一个稍大的正方体。
A. 8B. 4C. 29.一个长方体被挖掉一小块(如图),下面说法完全正确的是()A. 体积减少,表面积也减少B. 体积减少,表面积增加C. 体积减少,表面积不变10.如果正方体的棱长扩大到原来的3倍,则它的表面积扩大到原来的()倍。
A. 6B. 9C. 2711.正方体的棱长扩大到原数的3倍,表面积扩大到原数的()倍。
A. 3B. 9C. 612.棱长是6厘米的正方体,它的表面积和体积()A. 相等B. 不相等C. 不能相比二、填空题13.棱长是7cm的正方体的表面积是________cm2,体积是________cm3。
14.一个正方体木块,它的棱长是5dm,已知每立方分米重0.4千克,这个木块重________千克。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2 长方体无盖玻璃鱼缸
粉刷教室
只求五个面的面积
通常还要减去门窗的面积
3 组合图形的表面积
4 根据长方体展开图求它的表面积
经典易错题——表面积
5 将若干个物体拼合,表面积会减少。
将一个物体切分,表面积会增加。
6 两个物体表面积的比较。
下图两个物体的表面积相等。
锯成3段需切两次,会增加四个切面的面积。 一个切面的面积:32÷4=8(dm2)
整根长方体木料的横截面积 8×40=320(dm3)
一个正方体,如果它的高增加3cm,表面 积就要增加48cm2。这个正方体原来的体积 是( 64 )立方厘米。
因为下面是正方体,所以增加的四个面的面积相等。
一个面的面积:48÷4=12(cm2)。
3 等积变换问题。 形状不同,体积相等
把一个棱长是9cm的正方体铝块熔铸一个长方体 铁块,如果长方体的长是15cm,宽是10cm,高
是( 8.1 )厘米。
正方体体积:9×9×9=729(cm3)
长方体体积
长方体的高:729÷(15×10)=8.1ห้องสมุดไป่ตู้cm)
经典易错题——体积、容积
3 等积变换问题。 形状不同,体积相等
经典易错题——体积、容积
1 表面积与体积结合考察。
表面积是54 dm2的正方体,它的体积是( 27 )dm3。 正方体一个面的面积:54÷6=9(cm2) 所以正方体的棱长是 3cm 。 正方体的体积:3×3×3=27(cm3)
2 逆向思考问题,已知了体积,去求长 宽 高。
经典易错题——体积、容积
5cm 12m
把40 L水注入一个长50cm,宽40cm的长 方体鱼缸中,水深( 20 )厘米。
注入的水是长方体形状的,可以根据长方体 求高的方法。
40L=40dm3=40000cm3
h=V÷(a×b) =40000÷(50×40) =20(cm)
40cm 50cm
谢谢
每个面都是长方形,所以得到长 3cm 方形的长是12÷3=4(cm)。
长方形的长就是原来正方体的棱 长,所以原来正方体的体积是 4×4×4=64(cm3)。
有一堆240立方米的碎石,把这堆碎石铺在12米 宽的公路上,铺成5厘米厚的路面,能铺( 400米)。
高:5厘米=0.05米 宽:12米
由体积计算公式:V=a×b×h 得: a=V÷(b×h) =240÷(12×0.05) =400(m)
长方体和正方体
整理和复习
经典易错题——棱长
棱长总和
1、焊接一个正方体框架共用铁丝72cm,它 的表面积是( )cm2,它的体积是( )cm3。
棱长:72÷12=6(cm)
表面积:6×6×6=216(cm2)
体积:6×6×6=216(cm3)
2、把一个长9cm、宽5cm、高4cm的长方体
框架改做成一个正方体框架,这个正方体 框架的棱长是( )厘米。
上面是一个正方体, 不过只需求它侧面 的四个面的面积
下面是一个完整的 长方体,求出它的 2cm 六个面总面积
2cm 4cm
4cm
如图是一个长方体纸盒的展开图,根据图中提供 的信息,求出这个纸盒的体积.(单位:厘米)
长是10cm 宽是4cm 高是2cm 10×4×2=80(cm3)
三个棱长是2 dm的正方体,拼成一个长方 体后,表面积(减少了16平方分米 )。
小明在一个长是8dm,宽是5dm的长方体水槽中 放进一块石头(完全浸没),水面上升了8cm,这
块石头的体积有( 32 )dm3。
上升部分水的体积就等于石头的体积。
上升部分的水是长方体形状的。
8×5×0.8=32(dm3)。
常见易错题
求下面组合图形的表面积
(4×4+4×2+4×2)×2=64(cm2) 2×2×4=16(cm2) 64+16=80(cm2)
拼了两次,共减少了四个面。 减少的面积是2×2×4=16(dm2)
一个面的面积
将一个长6cm、宽4cm、高2cm的长方体切
成两个小长方体,表面积最多增加( 48 )平
方厘米。平行于最大面切,增加的面积最多,
切一次会增加两个切面的面积。
2cm 4cm 6cm
一根长方体木料长4 m,锯成相同的3段后表面 积 增加32 dm2,木料的体积是多少立方分米?
棱长总和不变 长方体棱长总和:(9+5+4)×4=72(cm)
正方体棱长:72÷12=6(cm)
经典易错题——棱长
3、用丝带捆扎一个长方体礼盒(如下图). 打结处的丝带长40厘米.捆扎这个礼盒至 少需要多长的丝带?
两长 两宽 四高 再加打结。 25×2+20×2+10×4+40=170(cm)
经典易错题——表面积
