无机化学-化学热力学基础
大一无机化学3章化学热力学基础习题解

第三章 化学热力学基础思考题与习题2-1 何谓物质的标准状态?答:物质的标准状态是在温度为T 及标准压力Pө(Pө=100 kpa )下的状态。
2-2 计算下列各体系由状态A 变化到状态B 时热力学能的变化(1) 吸收了2000KJ 热量,并对环境做功300KJ 。
(2) 向环境放出了12.54KJ 热量,并对环境做功31.34KJ 。
(3) 从环境吸收了7.94KJ 热量,环境对体系做功31.34KJ 。
(4) 向环境放出了24.5KJ 热量,环境对体系做功26.15KJ 。
解:(1)1700KJ 300KJ -KJ 2000==+=∆W Q U(2) -43.88KJ 31.34KJ -KJ 4.512=-=+=∆W Q U(3) KJ 8.293KJ 4.331KJ 4.97=+=+=∆W Q U(4) 1.64KJ 26.15KJ .5KJ 24=+-=+=∆W Q U2-3 某体系由状态Ⅰ沿途径A 变到状态Ⅱ时从环境吸热314.0 J ,同时对环境做功117.0 J 。
当体系由状态Ⅱ沿另一途径B 变到状态Ⅰ时体系对环境做功44.0 J ,问此时体系吸收热量为多少? 解:(1)由状态Ⅰ变到状态Ⅱ:J 0.197J 0.117J 0.3141=-=+=∆W Q U(2)由状态Ⅱ变到状态Ⅰ:122U J,0.44U W ∆-=∆-=J 0.1971222-=∆-=-=∆U W Q U J 0.1532-=Q2-4、在1标准压力下,100℃时1mol 液态水体积为18.8mL ,而1mol 水蒸气的体积为30.2ml ,水的汽化热为40.67KJ ·mol -1,计算100℃时在标准压力下由30.2g 液态水蒸发为水蒸气时的△H 和△U 。
解:68.23KJ l 40.67KJ.mo mol 18.030.2H1-P =⨯==∆Q()63.02KJ 103738.314mol 18.030.2-68.23KJ RT n -H U 3-=⨯⨯⨯=∆∆=∆ 2-5、甲苯,CO 2和水在298K 时的标准生成焓分别为48.0KJ·mol -1、-393.5KJ·mol -1和-286.0KJ·mol -1,计算298K 和恒压下10gCH 4 (g)完全燃烧时放出的热量。
无机化学-第五章-化学热力学基础

注:①G为广度性质,与参与过程的物质的量成正 比。
②逆过程G与正过程的G数值相等,符号相反。 等于各③反如应果一G个之反总应和是。多个反应的和,总反应的rG
化学热力学的四个重要状态函数
判断一个反应进行的方向时,如果: rG<0反应自发进行 rG>0反应不自发进行 rG=0平衡状态 当rG<0时(产物的G<反应物的G)该反应就自动 向生成产物的方向进行,在反应中反应物不断减 小而产物不断增加,G为广度性质,当G反应物=G产 物即rG=0时反应就不再朝一个方向进行了,这就 是化学反应的限度,即化学平衡。
状态函数。
化学热力学的四个重要状态函数
二、焓(H) 设一封闭体系在变化中只做体积功,不做其它功, 则U=Q+W中W代表体积功:-pV(N/m2×m3)
W=Fl=pSl=-pV
V=V2-V1 若体系变化是恒容过程(体积不变),即没有体积功 则W=0,U=Qv Qv为恒容过程的热量,此式表示在不做体积功的 条件下体系在恒容过程中所吸收的热量全部用来增 加体系的内能。
我们可以从体系和环境间的热量传递来恒量体系 内部焓的变化。
如果化学反应的H为正值,表示体系从环境吸收 热能,称此反应为吸热反应。即:
∑H反应物<∑H生成物 ∑H(生成物-反应物)>0 如果化学反应的H为负值,则表示体系放热给环 境,称此反应为放热反应。即:
∑H反应物>∑H生成物 ∑H(生成物-反应物)<0
rG=-RTlnKa
此式只表示在等温下,rG与K平衡在数值上的关 系。
∴rG=-RTlnKa+RTlnJa
=RTln(Ja/Ka)
《无机化学》第3版 宋天佑 第2章 化学热力学基础

此时,可以设计一个假想界面, 从分体积的概念出发,认为 VO 以内 是体系,以外是环境。
宇宙 体系和环境放在一起, 在热力学上称为宇宙。
按照体系和环境之间的物质及能量 的交换关系,可以将体系分为三类:
敞开体系、封闭体系和孤立体系
敞开体系 体系和环境之间 既有能量交换, 又有物质交换
封闭体系 体系和环境之间 有能量交换, 无物质交换;
折线 ABC 即是过程的 p-V 线。
p
16
1
V
1
16
图中两轴所表示的物理量的
单位之积为
105 Pa 10-3m3 =1.0 × 102 J
p
16
1
V
1
16
故图中的单位面积代表
1.0×102 J 体积功。
p
16
1
V
1
16
而 p-V 线下覆盖的面积即图
中阴影部分的面积为
1×(16 -1)=15 个 单位
p = 1105 Pa
恒温过程
p = 2105 Pa
V = 2 dm3
V = 1 dm3
V = V终 - V始 =1-2
= - 1 (dm3)
体积功 在热力学过程中, 体系对抗外压改变体积,产生体 积功。
在一截面积为 S 的 圆柱形筒内,理想气体 体系经历一热力学过程
截面积 S
I
受恒外力 F
蓄电池充电的化学反应, 是为了储存能量。
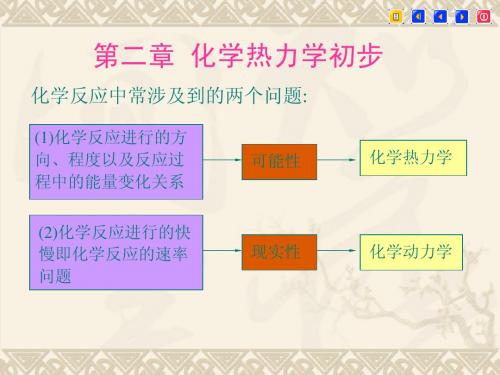
化学热力学,就是从化学反应的 能量出发,去研究化学反应的方向和 进行的限度的一门科学。
2. 1 热力学第一定律
2. 1. 1 热力学的基本概念和常用术语
体系 热力学中研究的对象, 称为体系。
环境 体系以外的其他部分, 称为环境。
无机化学[第二章化学热力学基础]课程预习.
![无机化学[第二章化学热力学基础]课程预习.](https://img.taocdn.com/s3/m/2f4778f2f8c75fbfc77db272.png)
第二章化学热力学基础一、热力学第一定律1.热力学的基本概念和常用术语(1)体系:热力学中称研究的对象为体系。
(2)环境:体系以外的其他部分。
按照体系与环境之间的物质和能量的交换关系,可分为三类:敞开体系体系与环境之间既有能量交换又有物质交换。
封闭体系体系与环境之间有能量交换但没有物质交换。
孤立体系(又称隔离体系) 体系与环境之间即无物质交换,又无能量交换。
(3)状态:由一系列表征体系性质的物理量所确定下来的体系存在的形式称为体系的状态。
(4)状态函数:借以确定体系状态的物理量称为体系的状态函数。
(5)过程:体系的状态发生变化,从始态变到终态,我们说体系经历了一个热力学过程,简称过程。
(6)途径:实现过程的每一种具体方式。
(7)体积功:体系由于体积的变化而做功称为体积功,即W=p·△V。
(8)热力学能:指体系内一切能量的总和,通常用U表示。
2.热力学第一定律(1)热力学第一定律的内容热力学第一定律的实质就是能量守恒。
更确切地说,热力学第一定律是能量守恒与转化定律在涉及热现象的宏观过程中的具体描述,其关系式为△U=Q - W式中,Q表示体系从环境中吸收热量;W表示体系对环境做的功。
(2)功和热热和功是能量传递的两种形式,它们不是状态函数。
Q>0,系统吸热;Q<0,系统放热。
W>0,环境对系统做功;W<0,系统对环境做功。
对定压过程中气体膨胀或被压缩所做的体积功来说W= -p ex(V2 - V1);系统被压缩,W>0;系统膨胀,W<0。
二、热化学1.化学反应的热效应化学反应的热效应可以定义为:在无非体积功的体系和反应中,当生成物与反应物的温度相同时,化学反应过程中吸收或放出的热量,化学反应热效应一般称为反应热。
(1)恒容反应热恒容反应热指在恒容过程中完成的化学反应的热效应,通常用Q V表示。
△U=Q V当△U>0时,Q V>0,则该反应是吸热反应;当△U<0时,Q V<0,该反应是放热反应。
无机化学(人卫版)第五章化学热力学基础
CO 2 (g)
mol △ rHm (2) = -282.98kJ· -1 计算298.15K下,下列反应的反应热:
1 O2 (g) C(s) 2
CO(g) △ rHm (3)
解法一: (利用 △ rHm (1) 由始态 CO2 g 到终态 途径1 的不同 途径)
2
解:利用Hess定律 △ rHm (3) C(s) O (g )
B —物质B的化学计量数
B为物质B的化学计量数,其量纲为一,反应物的
化学计量数为负值,而生成物的化学计量数为正值。
νA=-a, νB=-b, νY=y, νZ=z 。
例: 反应 1/2N2 + 3/2H2 = NH3 化学计量数 B分别为:
(NH3) = 1 ,(N2)= 1/2, (H2) = -3/2
mol △ rHm (298.15K) = -571.66kJ· -1
△ • 化学计量数不同时, rHm 不同。 1 H2(g)+ O2(g) H2O(g) 2 mol △ rHm (298.15K) = -241.82kJ· -1
2.3.3 盖斯(Hess)定律 △ rHm 始态 终态
△ rHm,1 △ rHm,2
结论: aA + bB → yY + zZ
rHm(T)
=Σν B fHm(生成物) +Σ νBfHm(反应物)
= Σν B fHm(B)
§2.4 热力学第二定律
2.4.1 化学反应的自发性
•水从高处流向低处; •热从高温物体传向低温物体;
•铁在潮湿的空气中锈蚀;
•锌置换硫酸铜溶液反应: Zn(s)+Cu2+(aq)
解: 该反应在恒温恒压下进行,所以
无机化学教学3章化学热力学基础PPT课件

反应自发性的判断
1 2
自发反应的定义
自发反应是指不需要外界作用就能自动进行的反 应。
自发性的判断依据
根据热力学第二定律,自发反应总是向着能量降 低、熵增加的方向进行。
3
自发性与焓变和熵变的关系
自发反应总是向着ΔH - TΔS < 0的方向进行,其 中ΔH为焓变,ΔS为熵变,T为绝对温度。
反应热的计算
表述
$Delta U = Q + W$,其中$Delta U$表示系统内能的变化,$Q$表示系统吸 收或放出的热量,$W$表示外界对系统做的功。
热和功的转化
热转化为功
当系统体积膨胀对外做功时,吸收的 热量会部分转化为对外做功。
功转化为热
当外界对系统做功使得系统体积压缩 时,外界所做的功会全部转化为系统 内的热量。
表述
熵增加原理指出,在封闭系统中,总熵(即系统熵与环境熵 的和)总是增加的。
卡诺循环与熵的概念
卡诺循环
卡诺循环是理想化的热机工作过程, 由四个可逆过程组成(等温吸热、等 温放热、绝热膨胀、绝热压缩)。
熵的概念
熵是描述系统混乱度或无序度的物理 量,其值越大,系统的无序度越高。
熵增加原理
表述
解释
应用
04 热力学第三定律
定义与表述
热力学第三定律通常表述为
在绝对零度时,任何完美晶体的熵值为零。
另一种表述为
不可能通过有限步骤将绝对温度降到绝对零度。
绝对熵的求算
根据热力学第三定律,绝对熵可以通 过计算完美晶体在绝对零度时的熵值 来获得。
在计算过程中,需要考虑晶体的原子 排列、分子振动等因素对熵值的影响。
热力学的主要概念
状态函数
无机化学之化学热力学基础优秀课件

几种常见的热力学过程
• 恒压过程(isobar process)
如果体系在状态变化过程中,且压力始终恒定, 则此变化过程称为恒压过程;
等压变化:只强调始态与终态的压力相同,且等 于环境压力,而对过程中的压力不作任何要求。
• 恒温过程(isothermal process)
如果体系的状态变化是在温度恒定的条件下进行 的,此变化称为恒温过程。
• 状态函数的特点
1)状态函数是状态的单值函数。 2)条件变化时,状态也将变化,但状态函数的变化值只
取决于始态和终态,而与状态变化的具体途径无关。
例:当系统由始态变到终 态时,系统的状态函
系统压力从 3pº变为 pº
数压力 P 和体积V 的
变化量与途径无关。
始 态
终 态
中间态Βιβλιοθήκη 3)当状态变化时,状态函数一定改变,但状态变化时, 状态函数并不一定全部改变。
开放体系 (open system)
有物质和能量交换
封闭体系 (closed system)
有能量无物质交换
孤立体系 (isolated system)
无物质和能量交换
(体系 + 环境)
3.1.2 状态与状态函数
状态 (state)
• 状态的定义
体系的状态是体系宏观物理和化学性质的综合表现。 体系的宏观性质包括:温度 ( T )、压力 ( p )、体
描述体系的状态不一定要用该体系的全部状态 函数,而用它的某几个状态函数就行,因为这些状 态函数间往往有一定的联系。
例如,要描述一理想气体所处的状态,只需知道 T、p、V 就够用,因为根据理想气体的状态方程 pV = nRT,此理想气体的物质的量 (n) 也就确定了。
无机化学 化学热力学基础1

(3) H正反应= H逆反应
31
3-1-2 热力学第一定律
(The first law of thermodynamics )
体系和环境之间的能量交换: 热传递 做功
在能量交换过程中,体系的内能 将发生变化。
32
1. 热力学第一定律: 自然界一切物质都具有能量,能量
有各种不同的形式,能够从一种形
式转化为另一种形式,从一个物体
• 过程着重于始态和终态; 而途径着重于具体方式。
15
状态函数的特点: 当体系的状态被改变时, 状态函数的变化只决定于体 系的始态和终态,而与变化 的途径无关。
16
始态T1
T = T2 T1
途径I
终态T2
冷却
冷却
加热
途径II
途径II
17
状态函数的变化
殊途同归变化等, 周而复始变化零。
37
3-2 热化学
把热力学理论和方法应用于化学反应 中, 讨论和计算化学反应的热量变化, 这门科学称为热化学.
3-2-1 3-2-2 3-2-3 3-2-4 3-2-5 化学反应的热效应 盖斯定律 生成热 燃烧热 从键能估算反应热()
38
3-2-1 化学反应的热效应
化学反应体系与环境进行能量交换的
26
5. 体积功(膨胀功) 体系反抗外压改变体积, 产生体积功。
设: 在一截面积为 S 的圆柱形筒内发生 化学反应, 体系反抗 外压 p 膨胀, 活塞从 I 位移动到 II 位。 由于体系反抗外压(p)做功(体系对环境做功), 体系失功,则
W体 = Fl = p•S•l = p•V
27
你的结论?
压强是体系的 强度性质。
13
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
4 / 39
无机化学
状态与状态函数
状态 由一系列表征系统性质的物理量所决定的 系统存在形式
状态函数 确定系统状态的各种宏观物理量
气体状态:压强 体积 温度 物质的量 等状态函数 状态确定 状态函数唯一
状态函数变化 取决于系统的初始状态 (始态) 最终状 态 (终态)
状态函数分类 广度性质 (质量) 强度性质 (压强)
▶ 等压过程 ▶ 等温过程 ▶ 等容过程 ▶ 绝热过程 ▶ 循环过程
∆p = 0 p = pe ∆T = 0 T = Te ∆V = 0 ∆Q = 0 始态=终态(状态函数变化?)
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
3 / 39
热力学第一定律
系统 研究对象 环境 系统以外与系统密切相关的周围部分
无机化学
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
5 / 39
过程与途径
过程 系统从始态到终态变化 途径 完成一个过程的具体步骤 区别 过程只与 始态 终态 相关
同一个过程可以有多种途径
无机化学
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
状态函数 确定系统状态的各种宏观物理量
气体状态:压强 体积 温度 物质的量 等状态函数
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
4 / 39
过程与途径
过程 系统从始态到终态变化 途径 完成一个过程的具体步骤
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
2 / 39
无机化学
化学热力学 (Chemical thermodynamics)
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
4 / 39
无机化学
状态与状态函数
状态 由一系列表征系统性质的物理量所决定的 系统存在形式
. .. . . ..
1 / 39
化学热力学 (Chemical thermodynamics)
无机化学
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. . . .... .... .... . . . . .... .... .... . .
热力学 研究热与其他形式的能量之间转化规律的 一门学科
化学热力学 利用热力学基本原理研究化学反应及其 伴随的物理变化 ▶ 能量变化 ▶ 反应方向 ▶ 反应程度 (Ch3 化学平衡)
化学动力学 反应速率 反应机理 (Ch4)
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
系统 能量交换 物质交换
敞开
√
√
封闭
√
×
ห้องสมุดไป่ตู้
孤立
×
×
人?宇宙?系统+环境?
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
3 / 39
无机化学
状态与状态函数
状态 由一系列表征系统性质的物理量所决定的 系统存在形式
状态函数 确定系统状态的各种宏观物理量
无机化学
Ch2 化学热力学基础 热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由能变 热力学在生物化学中的应用
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. . . .... .... .... . . . . .... .... .... . .
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
2 / 39
热力学第一定律
系统 研究对象 环境 系统以外与系统密切相关的周围部分
无机化学
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. .. . . ..
2 / 39
无机化学
化学热力学 (Chemical thermodynamics)
热力学 研究热与其他形式的能量之间转化规律的 一门学科
化学热力学 利用热力学基本原理研究化学反应及其 伴随的物理变化
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
. . . .... .... .... . . . . .... .... .... . .
. .. . . ..
2 / 39
无机化学
化学热力学 (Chemical thermodynamics)
热力学 研究热与其他形式的能量之间转化规律的 一门学科
化学热力学 利用热力学基本原理研究化学反应及其 伴随的物理变化 ▶ 能量变化 ▶ 反应方向 ▶ 反应程度 (Ch3 化学平衡)
无机化学
Ch2 化学热力学
热力学第一定律 热化学 热力学第二定律 化学反应的摩尔吉布斯自由 能变 热力学在生物化学中的应用
▶ 等压过程 ▶ 等温过程 ▶ 等容过程 ▶ 绝热过程 ▶ 循环过程
∆p = 0 p = pe ∆T = 0 T = Te ∆V = 0 ∆Q = 0 始态=终态(状态函数变化?)
