范里安-博弈论
范里安第二十一章博弈论

(-1,1)
(1,-1)
背面
(1,-1)
(-1,1)
23
纳什均衡
混合战略
参与者i的一个混合战略是指在其纯战略空间 Si 中的一个概率分布。
——确定选采取某一个纯战略的概率。 纯战略空间: S 混合战略:
i
{正面,背面}
i ( p,1 p)
p [0,1]
24
纳什均衡
纳什均衡:
29
完全信息动态博弈
例:敲诈博弈 参与者1的战略空间:{给,不给}
参与者2的战略空间:{(R,R),(R,L),(L,R),(L,L)} R:不拉;L:拉
参与者2 (R,L) 给 (0,1000) (R,R) (0,1000) (1000,0) (L,R) (L,L)
(,)
(1000,0)
si S i ,对于其他参与者的每一个 s i 的收益都不小于选择 的收
si Si , si S i
, s i ) ui (s , s i ) u ( s i i
——理性的参与者一定会选择占优战略
10
纳什均衡
占优战略
(招认,招认) 囚徒困境
囚徒2
沉默 招认
混合战略
参与者 i 选择正面的概率为P 参与者 j 选择正面的概率为q 正面(z) 参与者1 背面(f) 参与者1的期望收益: 猜硬币 参与者2 正面(z) 背面(f)
(-1,1)
(1,-1)
(1,-1)
(-1,1)
u1 ( p, q) pqu1 (z, z ) p(1 q)u1 (z, f )
G (T ) 有限次重复博弈 由唯一的子博弈精练均衡 :即 将阶段博弈的纳什均衡在每阶段重复进行。
范里安-微观经济学现代观点(第7版)-28博弈论(含习题解答)

Chapter 28: Game TheoryIntermediate Microeconomics:A Modern Approach (7th Edition)Hal R. Varian(University of California at Berkeley)第28章:博弈论(含习题解答)含习题解答)中级微观经济学:现代方法(第7版)范里安著(加州大学伯克利)曹乾译(东南大学caoqianseu@)简短说明:翻译此书的原因是教学的需要,当然也因为对现行中文翻译版教材的不满。
市场中的翻译版翻译生硬错误百出。
此次翻译的错误是微不足道的,但仍欢迎指出。
仅供教学和学习参考。
28博弈理论我们在上一章阐述的寡头理论,是企业间策略性互动的经典经济理论解释。
但这只是冰山一角。
经济行为人(agents)的策略性互动有多种方式,经济学家借助博弈理论(game theory)这个工具已研究了很多种策略性互动的行为。
博弈理论关注的是策略性互动的一般分析。
人们可使用博弈理论研究室内游戏(parlor games)、政治协商和经济行为(一)。
在本章,我们将简要分析这一迷人的学科,目的是让你感受一下它是如何运行的,以及让你初步知道如何使用博弈理论分析寡头市场中的经济行为。
28.1博弈的收益矩阵策略性互动可能涉及很多选手和很多策略,但是我们仅限于分析两个选手之间的博弈,而且限于分析策略的数量有限的情形。
这样做的好处是可以用收益矩阵(payoff matrix)描述博弈。
最好举例进行分析。
假设两人玩一种简单的游戏。
选手A在纸上写出“上”或“下”。
与此同时,选手B独立地写出“左”或“右”。
在两人写好后,经过分析,将他们的收益标记于表28.1中。
若A 选上且B选左,我们看矩阵的左上角的小方格。
在该小方格中,A的收益是第一个数,B 的收益是第二个数。
类似地,如果A选下B选右,则A得到收益为1,B得到的收益为0.表28.1:一个博弈的收益矩阵选手A有两个策略:上或下。
范里安《微观经济学(高级教程)》(第3版)课后习题-博弈论(圣才出品)

第15章博弈论1.计算便士匹配博弈中的所有纳什均衡。
Calculate all the Nash equilibria in the game of Matching Pennies.答:表15-1为便士匹配博弈的支付矩阵。
表15-1便士匹配博弈这是一个典型的零和博弈。
在零和博弈里,不存在纯策略纳什均衡,唯一的混合策略纳什均衡为每一局中人以12/的概率选择正面或反面,此时混合策略纳什均衡的收益均为0。
根据同等支付原则,此时以12/的概率选择正面或反面的策略为混合策略纳什均衡。
2.在有限重复囚犯悖论博弈中,证明了一个纳什均衡为每一回合都背叛,请证明它事实上也是占优均衡。
In a finitely repeated Prisoner’s Dilemma game we showed that it was a Nash equilibrium to defect every round.Show that,in fact,this is the dominant strategy equilibrium.答:令r和2r为行参与人的两个策略。
1r严格占优于2r是说,不论列参与人选择何种策1略,行参与人选择r得到的支付至少和他选择2r得到的支付一样多,并且对列参与人做的一1些选择,行参与人选择r得到的支付要严格大于选择2r的支付。
1一个占优策略均衡是指均衡的策略组合对每个人而言都是其占优策略。
表15-2囚徒困境在表15-2中,如果行选择背叛,当列选择合作时,行得到4大于列的0,当列选择背叛时,行得到1等于列的1,因此选择背叛对行来说是占优策略;同理可以证明对列来讲,选择背叛也是占优策略。
对于有限重复的博弈,在最后一轮回合中,选择背叛行为是不可能被报复或受到惩罚的。
于是,最后一轮回合出于理性的占优策略就是选择背叛。
逆推到倒数第二回合,由于每个参与者都知道下一回合是背叛,因此,这一回合的占优策略也是选择背叛。
微观经济学:现代观点(范里安-著)48题及答案汇编

第一部分 消费者选择理论1.有两种商品,x1和x2,价格分别为p1和p2,收入为m 。
当11x x ≥时,政府加数量税t,画出预算集并写出预算线2. 消费者消费两种商品(x1,x2),如果花同样多的钱可以买(4,6)或(12,2),写出预算线的表达式。
3.重新描述中国粮价改革(1)假设没有任何市场干预,中国的粮价为每斤0。
4元,每人收入为100元。
把粮食消费量计为x ,在其它商品上的开支为y ,写出预算线,并画图。
(2)假设每人得到30斤粮票,可以凭票以0。
2元的价格买粮食,再写预算约束,画图。
(3)假设取消粮票,补贴每人6元钱,写预算约束并画图。
4. 证两条无差异曲线不能相交5. 一元纸币(x1)和五元纸币(x2)的边际替代率是多少? 6. 若商品1为中性商品,则它对商品2的边际替代率?7. 写出下列情形的效用函数,画出无差异曲线,并在给定价格(p 1,p 2)和收入(m )的情形下求最优解。
(1)x 1=一元纸币,x 2=五元纸币。
(2)x 1=一杯咖啡,x 2=一勺糖, 消费者喜欢在每杯咖啡加两勺糖。
8. 解最优选择 (1)21212(,)u x x x x =⋅(2)2u x =+9. 对下列效用函数推导对商品1的需求函数,反需求函数,恩格尔曲线;在图上大致画出价格提供曲线,收入提供曲线;说明商品一是否正常品、劣质品、一般商品、吉芬商品,商品二与商品一是替代还是互补关系。
(1)212x x u += (2)()212,m in x x u =(3)ba x x u 21⋅=(4) 12ln u x x =+,10. 当偏好为完全替代时,计算当价格变化时的收入效用和替代效用(注意分情况讨论)。
11. 给定效用函数 (,)x y xy =,p x =3,p y =4,m=60,求当p y 降为3时价格变化引起的替代效应和收入效应。
12. 用显示偏好的弱公理说明为什么Slutsky 替代效应为负。
范里安《微观经济学:现代观点》第9版章节题库(博弈论的应用)【圣才出品】

范里安《微观经济学:现代观点》第9版章节题库第30章博弈论的应用1.保证博弈和斗鸡博弈都是协调博弈,可见二者并没有区别。
()【答案】F【解析】虽然保证博弈和斗鸡博弈同属协调博弈,但也有区别,比如:保证博弈中,与做不同的事情相比较,博弈双方做相同的事情时境况较好;而在斗鸡博弈中,博弈双方做相同事情时的境况要劣于做不同事情时的境况。
2.同时行动的博弈就是指博弈双方同时进行选择的博弈。
()【答案】F【解析】同时行动的博弈中,每个参与人必须在不知道对方所做选择(不论他正在选择还是已经选择了)的情况下,做出自己的选择。
这里的关键是“不知道”对方的选择,而不是强调时间相同。
3.古诺均衡中的每个参与人在决策时都假定对手的产量不变,而这是不现实的,因此,古诺均衡是错误的。
()【答案】F【解析】古诺均衡是指如果对方采取古诺产量,则本方也采取古诺产量,在此情况下,双方都没有改变产量的动机。
在古诺均衡的情况下,由于对方没有改变产量的动机,故本方假定对方产量不变是正确的。
4.两企业事先无串谋,其平均成本分别为C1和C2,且C1<C2,则其纳什均衡下的价格为P*=C1。
()【答案】F【解析】当成本相差不大时,根据价格竞争的伯特兰模型,价格竞争的结果应该为P*=C2-ζ;当成本相差较大时,价格竞争的结果很可能是厂商1在P*=C1实施垄断定价,以实现利润最大化。
5.在双人博弈中,给定收益矩阵如下,求满足什么条件时该博弈不存在纯策略均衡。
解:纯策略均衡是指每个参与者只选择一种策略并始终坚持这个选择。
如果只关注该博弈的纯策略均衡,一个非常行之有效的方法为箭头标注法:上下方向箭头表示“行博弈者”不同策略下的收益比较结果;左右方向箭头表示“列博弈者”不同策略下的收益比较结果;箭头共同所指方向为博弈的纯策略均衡。
若b>d且a>e,则(U,L)为纯策略均衡;若c>g且d>b,则(U,R)为纯策略均衡;若f>h且a<e,则(D,L)为纯策略均衡;若g>c且h>f,则(D,R)为纯策略均衡。
范里安 中级微观经济学 名词解释

内生变量:其均衡值(解)在模型内部决定。
外生变量:其均衡值(解)在模型外部决定。
最优化原理:人们总是选择他们能支付得起的最佳消费方式。
狭义均衡原理:价格会自行调整,直到人们的需求数量与供给数量相等。
广义均衡原理:经济主体的行为必须相互一致。
保留价格:某人愿意接受、购买有关商品的最高价格。
需求曲线:一条把需求量和价格联系起来的曲线,描述了每一个可能价格上的需求数量。
均衡价格:住房需求量等于住房供给量时的价格。
比较静态学:研究均衡价格和数量在基础条件变化时如何变化的理论。
垄断:市场被某一产品的单一卖主所支配的情况。
完全价格歧视(价格歧视垄断者):垄断者对每一个租赁者收取等于“保留价格”的房租。
一般垄断者:收取相同价格的垄断者。
超额需求:愿意按价格P(max)租房的人多余可供给的住房。
住房配置方法:竞争市场、价格歧视垄断者、一般垄断者、房租管制。
长期均衡:长期中,住房的供给量将会随着价格的变化而变化。
如果可以找到一种配置方法,在其他人的境况没有变坏的情况下,的确能使一些人的境况变得更好一些,那么这里就存在帕累托改进。
如果一种配置方法存在帕累托改进,它就称为帕累托低效率。
如果一种配置方法不存在任何的帕累托改进,就称为帕累托有效率。
预算集:在给定价格和收入的情况下消费者能够负担得起的所有消费束组成的集合。
预算线:在给定价格和收入的情况下正好可以将消费者的收入用完的消费束组成的集合(p1x1+ p2x2 =m)。
预算线斜率的含义:表示市场愿意用商品1来“替代”商品2的比率;在继续满足预算约束的情况下,为增加1单位商品1而必须放弃的商品2的数量(机会成本)。
计价物:如果设定商品2的价格为1,并适当调整商品1的价格和消费者收入,使得预算集不发生改变,就称商品2是“计价物”。
从量税:根据消费者购买商品的数量征收的税。
从价税:根据消费者购买商品的价值征收的税。
总额税:无论消费者行为如何,政府取走的一笔固定金额。
(从量税和从价税率的变化将使预算线的斜率更陡峭;总额税的变化将使预算线向内平行移动。
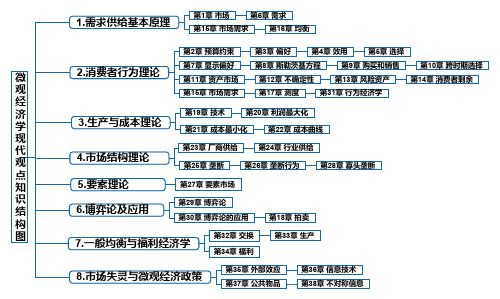
范里安微观经济学现代观点-知识结构图
者
基数效用
离散品
行
效用函数
序数效用
为
完全替代和互补
理 论
第4章 效用 无差异曲线的推导 拟线性偏好
一
柯布-道格拉斯偏好
边际效应和边际替代率
最优选择的条件:掌握线性及非线性条件规划问题 求解。
最优选择
最优选择的类型:唯一切点最优、折拗偏好无切 点、边界最优、切点不唯一。
消费者的需求
完全替代和完全互补
第5章 选择
论
非合作博弈
不完全信息静态博弈 贝叶斯纳什均衡
及
合作博弈
动态博弈
完全信息动态博弈
子博弈精炼纳什均衡
应
不完全信息动态博弈 精炼贝叶斯纳什均衡
用
合作博弈:又称协调博弈,参与人在他们协调行动
时获得的收益大于不协调时的收益
第30章 博弈论的应用
竞争博弈:零和博弈,在这类博弈中,博弈一方的 收益等于另一方的算是
产 与
长期利润最大
成
利润最大化弱公理
本
成本最小的求解
理 论
第21章 成本最小化
条件要素需求函数和成本函数 短期成本与长期成本
显示成本最小化公理
总成本:STC,TVC,TFC
短期成本曲线 平均成本:SAC,AVC,AFC
第22章 成本曲线
边际成本:SMC 总成本:LTC
长期成本曲线 平均成本:LAC
边际成本:LMC
1.需求供给基本原理
第1章 市场
第6章 需求
第15章 市场需求
第16章 均衡
第2章 预算约束
第3章 偏好
第4章 效用
第5章 选择
第7章 显示偏好
第8章 斯勒茨基方程
范里安《微观经济学(高级教程)》(第3版)章节题库-博弈论(圣才出品)

11.古诺均衡中的每个参与人在决策时都假定对手的产量不变,而这是不现实的,因 此,古诺均衡是错误的。( )
【答案】F 【解析】古诺均衡是指如果对方采取古诺产量,则本方也采取古诺产量,在此情况下, 双方都没有改变产量的动机。在古诺均衡的情况下,由于对方没有改变产量的动机,故本方 假定对方产量不变是正确的。
3.如果某博弈存在纯策略均衡,那么不可能同时存在非退化的混合策略均衡。( ) 【答案】F
1 / 28
圣才电子书 十万种考研考证电子书、题库视频学习平台
【解析】纯策略均衡是指每个参与者只选择一种策略并始终坚持这个选择。混合策略是 指参与人使他们的策略选择随机化,即对每项选择都指定一个概率,并按照这些概率选择策 略。混合纳什均衡是指给定其他参与人的策略选择概率,每个参与人都为自己确定了选择每 一种策略的概率。混合策略均衡总是存在的,纯策略均衡的存在与否并不影响混合策略均衡 的存在。
9.囚徒的困境说明了个人的理性选择不一定是集体的理性选择。( ) 【答案】T 【解析】在囚犯难题中,每个囚犯都选择了自己的最优策略,所以个人理性得到了体现。 但最后的结果是可以进行帕累托改进的,所以并不是集体理性的选择。
10.同时行动的博弈就是指博弈双方同时进行选择的博弈。( ) 【答案】F 【解析】同时行动的博弈中,每个参与人必须在不知道对方所做选择(不论他正在选择 还是已经选择了)的情况下,做出自己的选择。这里的关键是“不知道”对方的选择,而不 是强调的时问相同。
8.纳什定理告诉我们纳什均衡解存在且稳定。( ) 【答案】F 【解析】纳什定理即指纳什均衡存在性定理,指如果一个对策的参与人是有限的,并且 每个参与人只有有限的策略,则该对策至少存在一个纳什均衡。但该定理没有指出解是否唯 一,一个对策可能存在多个纳什均衡;也没有指出解是否稳定。而且,很多情况下,纳什均 衡解都是不稳定的。如性别战中的均衡解就是两个不稳定的纯纳什均衡解。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
序贯博弈的例子
参与者 B
LR
U (3,9) (1,8)
参与者 A
D (0,0) (2,1)
假设这个博弈为序贯博弈,A为领导者而B为追随 者。我们可以把这个博弈的拓展形式写出来。
序贯博弈的例子
A
U B
D B
A 先行动 B 后行动
L
RL
R
(3,9) (1,8) (0,0) (2,1)
(U,L) 为一个纳什均衡。 (D,R)也是一个纳什均衡。 这两个均衡哪个更有可能发生?
第二十八章
博弈论
博弈是什么?
一个博弈包含: 一些参与者 每个参与者的策略 每个参与者选择不同决策行为的收益矩阵。
两人博弈的一个例子
参与者A 和 B。 A 可以采取两种行为:“上” 和 “下”。 B 可以采取两种行为: “左” 和 “右”。 包含了四种可能决策组合支付的表格称为博弈
参与者 A
D (0,0) (2,1)
参与者A 已经被考虑了上或者下的决策,但没有把这
两种策略联合起来考虑。例如,仅做出单纯的上或下 决策。上和下为参与者A的纯策略。
类似地,左和右为参与者B的纯策略。
序贯博弈的例子
参与者 B
LR
U (3,9) (1,8)
参与者 A
D (0,0) (2,1)
因此,(U,L)和(D,R) 为纯策略纳什均衡。是否每一个 博弈都至少有一个纯策略纳什均衡?
(U,L)是否为一个纳什均衡?
(U,R)是否为一个纳什均衡? (D,L)是否为一个纳什均衡? (D,R) 是否为一个纳什均衡?
不是。 不是。 不是。
不是。
混合策略
参与者A选择一个概率分布(pU,1-pU),表示参与者A 有pU的概率选择策略上,有1-pU的概率选择策略下; 而不是单纯的选择上或者下的策略。
我们的例子中有两个纳什均衡 (U,L) 和(D,R)。
两人博弈的例子
参与者 B
LR
U (3,9) (1,8)
参与者 A
D (0,0) (2,1)
(U,L) 和 (D,R) 为此博弈的纳什均衡。但是我们 发现: 对两个参与者来说,(U,L) 比 (D,R) 更受 偏好。我们是否一定仅会看到 (U,L)的博弈均衡 结果?
序贯博弈的例子
A
U B
D B
ห้องสมุดไป่ตู้A 先行动 B 后行动
L (3,9)
RL (1,8) (0,0)
R
因此(U,L)很可能为 均衡结果。
(2,1)
假如A先选择决策U ,B后选择策略L;A 所得收益为3。 假如A先选择策略D,B后选择策略R;A 所得收益为2。
序贯博弈的例子
参与者 B
LR
U (3,9) (1,8)
纯策略
参与者 B
L
R
U (1,2)
参与者 A
D (0,5)
(0,4) (3,2)
这是一个新的博弈。是否存在纯策略的纳什均衡?
纯策略
参与者 B
L
R
U (1,2)
参与者 A
D (0,5)
(0,4) (3,2)
因此当采取纯 策略时,该博 弈没有纳什均 衡。但是这个 博弈在采取混 合策略时有一 个纳什均衡。
L
R
U (1,2)
参与者 A
D (0,5)
(0,4) (3,2)
这个博弈没有纯策略纳什均衡,当有混合策略纳什均衡 。混合纳什均衡结果是如何计算的?
混合策略
U, pU
参与者 A
D, 1-pU
参与者 B
L, pL R, 1-pL (1,2) (0,4)
(0,5) (3,2)
混合策略
A选择上策略的预期收 益为pL。 A选择下策略的预期收 益为3(1 - pL)。
和下的策略所得收益无差异。
混合策略
参与者 B
L, 3/4 R, 1/4
U, pU (1,2)
参与者 A
D, 1-pU (0,5)
(0,4) (3,2)
混合策略
B选择左的策略的预期收
益为2pU + 5(1 - pU)。 B选择右的策略的预期收
决策时机
在上面来两个例子中,参与者同时做出他们的 决策。
这样的博弈称为同步博弈。 但博弈过程也可能表现为参与者按一定顺序作
出决策行动。首先行动的参与者称为领导者, 后行动的参与者称为追随者。
序贯博弈的例子
有时一个博弈可能含有几个纳什均衡,很难确 定哪一种均衡结果更有可能发生。
当一个博弈为一个序贯博弈时,那么就有可能 其中的一个纳什均衡比其它均衡更有可能发生。
U, pU
参与者 A
D, 1-pU
参与者 B
L, pL R, 1-pL (1,2) (0,4)
(0,5) (3,2)
假如 pL > 3(1 - pL) 那么A仅选择上的策略,但是当A采 用上的纯策略时没有纳什均衡。 假如 pL < 3(1 - pL) 那么A仅选择下策略,但是当A采用下 的纯策略时没有纳什均衡。
囚徒困境
为了了解帕累托偏好结果是否一定就是一个博 弈的结果。考虑一个很有名的囚徒困境博弈问 题。
囚徒困境
克莱德
S
C
S (-5,-5) (-30,-1)
邦妮
C (-1,-30) (-10,-10)
这个博弈的可能结果是什么样子?
唯一的纳什均衡为 (C,C),尽管 (S,S) 能使得邦妮 和克莱德的处罚更轻。这个唯一的纳什均衡是无 效率的。
的收益矩阵。
两人博弈的一个例子
参与者 B
LR
U (3,9) (1,8)
参与者 A
D (0,0) (2,1)
这是博弈的 收益矩阵
左边显示A的收益 右边显示B的收益
两人博弈的一个例子
参与者 B
LR
U (3,9) (1,8)
参与者 A
D (0,0) (2,1)
哪种策略组合结果会最终出现?
纳什均衡
博弈论中的策略组合中,每个参与者的决策都 是对其它参与者决策的最佳反应决策时所达到 的均衡称为 纳什均衡。
混合策略
存在纳什均衡的必要必要
条件为pL = 3(1 - pL) pL = ¾ ;B采用左和右的
U, pU
参与者 A
混合策略时必须要使A对
D, 1-pU
采取上和下的策略所得收
益无差异。
参与者 B
L, pL R, 1-pL (1,2) (0,4)
(0,5) (3,2)
存在纳什均衡的必要必要条件为pL = 3(1 - pL) pL = ¾ ;B采用左和右的混合策略时必须要使A对采取上
参与者A混合了上和下的纯策略。 概率分布(pU,1-pU)为参与者A的混合策略。
混合策略
类似地,参与者B选择概率分布 (pL,1-pL),表示有 pL的概率他会选择左,有1-pL的概率他会选择右。
参与者B混合了左和右的纯策略。 概率分布(pL,1-pL)为参与者B的混合策略。
混合策略
参与者 B
