Peck法计算的盾构隧道地面沉降量及沉陷槽计算公式
Peck 公式

Peck公式1969年,Peck在分析了大量地表沉降数据后,提出了地表沉降槽符合高斯分布的概念。
他认为地层变形由地层损失引起,施工引起的地面沉降是在不排水的条件下发生的,从而假定地表沉降槽体积等于地层损失体积。
如今这个公式在世界上广泛应用,成为预估沉降槽的经典公式。
s为地面任一点的沉降值,单位为mm;s为地面沉降的最大值,位于沉降曲线的对称中心上(对应于隧洞轴线位置),单位为mm;m axx为从沉降曲线中心到所计算点的距离,单位为m;i为从沉降曲线对称中心到曲线拐点(反弯点)的距离,一般称为“沉降槽宽度”,单位为m;i3通过对正态分布函数二次求导,令其等于0求得;V为隧道单位长度地层损失,单位为mm/3;V为地层体积损失率,即单位长度地层损失占单位长度盾构体积的百分比;这个参数的取值依赖地l方经验。
其中,i一般由查图表或者经验公式得来,以下列举了一些关于沉降槽宽度系数i的公式(一)Peck通过对大量地表沉降数据和有关工程资料的分析后,得出i为沉降槽宽度系数,单位为m;Z为隧道深度,单位为m;β为隧道周围地层内摩擦角(二)O’Reilly和New提出一种简便的定义i值的方法,即i和隧道深度Z之间存在以下简单的线性关系i为沉降槽宽度系数,单位为m;K为沉降槽宽度参数,这要取决于土性;Z为隧道深度,单位为m(三Clough和Schimidt 在其关于软黏土隧道的着作中,提出饱和含水塑性粘土中的地面沉降槽宽度系数i 由如下公式求得i 为沉降槽宽度系数,单位为m ;R 为隧道半径,单位为m ;Z 为隧道深度,单位为m(四)Attwell 假定沉降槽曲线正态分布,给出估算地表沉降的经验公式i 为沉降槽宽度系数,单位为m ;R 为隧道半径,单位为m ;Z 为隧道深度,单位为mK 和z 为统计系数(五)藤田收集了大量的,涉及多种盾构形式的统计资料后,给出以下公式i 为沉降槽宽度系数,单位为m ;R 为隧道半径,单位为m ;m ax s 为地面沉降的最大值,单位为mm;A 为沉降槽断面积,单位为2m ;A 为隧道断面积,单位为2m。
地铁隧道盾构法施工引起地表沉降分析论文

地铁隧道盾构法施工引起的地表沉降分析摘要:随着我国地铁建设的不断发展,在地下工程施工中人们越来越重视盾构掘进法开挖隧道引起的地表沉降对地面建筑物的影响,而这个问题的关键是要对地表沉降进行预估。
本文论述了peck横向沉降槽经验公式,并与相关工程相结合深入探讨了盾构掘进法施工隧道对地表沉降影响,并提出相关建议。
关键词:盾构法施工、地表沉降、分析中图分类号:tf351文献标识码: a 文章编号:一、前言现阶段,盾构法施工已成为国内城市地铁隧道施工中一种重要的施工方法。
和其他施工方法一样,由盾构法施工导致的地表沉降及对周围环境产的影响是盾构法施工的一个重要问题。
目前国内外专家学者对隧道施工引起地表沉降的预测方法主要有:经验公式法、模型试验法、数值分析法、理论预测法等。
在实际工程中主要是以建立在实测数据基础上的经验公式法为主,但是这种方法大都局限于预测地表面处的位移,在指导施工中具有很大的局限性。
而数值模拟法能动态反应盾构推进过程中土层中各点变形随时间的变化情况,而且可以对影响地表的许多因素进行直观的分析。
二、peck横向沉降槽经验公式沉降计算中最经典、常用的公式是peck公式。
peck认为,不排水情况下隧道开挖所形成的地表沉降槽的体积应等于地层损失的体积;地层损失在整个隧道长度上均匀分布,隧道施工产生的地表沉降横向分布近似为一正态分布曲线(如下图1)。
横向地表沉降的预估公式以及最大沉降量的计算公式为:式中:s(x)为距隧道中心轴线为x处的地面沉降,m; i 为地表沉降槽宽度,即曲率反弯点与中心的距离,m;smax为隧道轴线上方地表最大沉降量,m;vl为盾构隧道单位长度的地层损失量,m3/ m。
图 1地表横向沉降分布曲线反弯点i处的沉降量s≈0.61smax,最大曲率半径点的沉降量s ≈0.22smax。
沉陷槽断面积a≈。
想要预测地面沉降量,必须先估计出地层损失量。
在工程实践中,地层损失量与盾构种类、操作方法、地层条件、地面环境、施工管理等因素有关,一般难以正确估计。
Peck法计算的盾构隧道地面沉降量及沉陷槽计算公式

8. 1. 4地层变形预测与分析通常设汁阶段的地面沉降预测方法可分为两类,一是根据实测数据的统汁方法-Peck公式是其典型代表:二是采用有限元和边界元的数值方法。
采用Peck法计•算的盾构隧道地面沉降量及沉陷槽计算公式如下式;其沉陷槽横向分布见图。
沉降槽横向分布图S(x) = Smaxcxp(—2?)式中:V—地层损失(地表沉降容积);i—沉降槽曲线反弯点;z—隧道中心埋深根据本标段的地质条件和埋深等,得i=6.9m, III此根据以往的工程实践及经验公式,沉陷槽宽度B~5i,可得单个隧道盾构推进引起的地表横向沉陷槽宽度约为35m,两座隧道盾构推进引起的地表横向沉陷曲线叠加后其沉陷槽宽度约为50m,并且沉陷槽的主要范围在隧道轴线两侧6m范围内,离轴线3n)的沉降量约为最大沉降量的60%〜70%,离轴线6m的沉降量约为最大沉降量的25%o地层损失V值主要是山盾尾空隙引起的土体损失量,它与盾构机盾壳厚度、盾构推进时粘附在盾构上的土体厚度及注浆量等有关,即V二V尾+V粘-V浆盾构推进时粘附在盾构钢板上的土体厚度约为20~40mm,盾壳用度为70mm, 则:V 二V 尾+V 粘-V 浆二1. 36+0. 58 a-(1. 36+0. 58) Pa为折减系数,P为同步注浆的充填系数。
取 a =0.6 B 二0. 5 得V二0. 73m2山此可得地表最大沉陷值:Smdx二23. 4mm最大斜率:Qmdx二0.0013以上分析值主要是在以往工程经验基础上结合本地铁盾构标段的实际惜况,隧道埋深16m左右情况下得出的,最大沉降量满足规范和标书要求。
虽然地表沉降形态是大体相同或相似的,但其最大沉降量总是随着施工工况和地质条件的改变而千差万别,U询控制沉降的主要手段是同步注浆和二次注浆,而注浆的环节常有各种各样的问题发生,如缺量、过量、滞后、漏浆等等,不同的沉降情况常是施工工况和工作状态的反映,同时不同的地质条件沉降亦有所不同,如粉砂土较粘土隆降起量要少,沉降速率要快,淤泥质粘土后期固结沉降则要大点。
Peck公式(可编辑修改word版)

Peck 公 式1969 年,Peck 在分析了大量地表沉降数据后,提出了地表沉降槽符合高斯分布的概念。
他认为地层变形由地层损失引起,施工引起的地面沉降是在不排水的条件下发生的,从而假定地表沉降槽体积等于地层损失体积。
如今这个公式在世界上广泛应用,成为预估沉降槽的经典公式。
x 2s = s max exp[-2i 2 ]s max =s 为地面任一点的沉降值,单位为 mm ;s max 为地面沉降的最大值,位于沉降曲线的对称中心上(对应于隧洞轴线位置),单位为 mm ;x 为从沉降曲线中心到所计算点的距离,单位为 m ;i 为从沉降曲线对称中心到曲线拐点(反弯点)的距离,一般称为“沉降槽宽度”,单位为 m ;V 2i3i 通过对正态分布函数二次求导,令其等于0 求得;V 为隧道单位长度地层损失,单位为m3 / m ;V R2V =l4V为地层体积损失率,即单位长度地层损失占单位长度盾构体积的百分比;这个参数的取l值依赖地方经验。
其中,i 一般由查图表或者经验公式得来,以下列举了一些关于沉降槽宽度系数i 的公式(一)Peck 通过对大量地表沉降数据和有关工程资料的分析后,得出Zi =2tan(45。
-)2i 为沉降槽宽度系数,单位为m;Z 为隧道深度,单位为m;β为隧道周围地层内摩擦角(二)O’Reilly 和New 提出一种简便的定义i 值的方法,即i 和隧道深度Z 之间存在以下简单的线性关系i =KZi 为沉降槽宽度系数,单位为m;K 为沉降槽宽度参数,这要取决于土性;Z 为隧道深度,单位为m土性K 值(三)Clough 和Schimidt 在其关于软黏土隧道的著作中,提出饱和含水塑性粘土中的地面沉降槽宽度系数i 由如下公式求得i= ( Z)0.8R 2Ri 为沉降槽宽度系数,单位为m;R 为隧道半径,单位为m;Z 为隧道深度,单位为m(四)Attwell 假定沉降槽曲线正态分布,给出估算地表沉降的经验公式i=K ( Z )nR 2Ri 为沉降槽宽度系数,单位为m;R 为隧道半径,单位为m;Z 为隧道深度,单位为mK 和z 为统计系数(五)藤田收集了大量的,涉及多种盾构形式的统计资料后,给出以下公式2s max R 2 i = ( ∆A ) Ai 为沉降槽宽度系数,单位为 m ; R 为隧道半径,单位为 m ; s max 为地面沉降的最大值,单位为 mm;∆A 为沉降槽断面积,单位为 m 2 ;A 为隧道断面积,单位为 m 2。
Peck计算公式

(1)经验公式法
1969年,美国的Peck 在对大量隧道开挖地表沉降的实测数据进行分析的基础上,系统地提出了地层损失的概念和估算隧道开挖地表下沉的实用方法,即著名的Peek 公式[23]。
此后,Peck 本人及其他学者和工程技术人员作了大量工作,使之成为目前应用最为广泛的预计隧道施工地表沉降的方法。
()2max 2exp 2x S x S i ⎛⎫=- ⎪⎝⎭
max 2.52s s V V S i
i π=≈
图8 隧道上部沉降槽断面形状(Peck)
Peck 公式有s V 和i 两个参数,合理确定这两个参数对于正确预测地面沉降的
量值和分布情况起着至关重要的作用,其表达式为:
()
2tan 452i kz ϕπ==︒- 2s l V V R π=
式中:S(x)为距离隧道中心轴线为x 处的地表沉降(mm);S max 为隧道中心线处的地表最大沉降(mm);i 为地表沉降槽宽度系数(m),也即隧道中心至沉降曲线反弯点的距离;k 为沉降槽宽度系数;z 为隧道中心埋深;φ为土体内摩擦角;V s 为施工引起的隧道单位长度的地层损失量(m 3/m),也即隧道施工中实际开挖的岩土体的体积与竣工隧道的体积之差;V l 为地层体积损失率,即单位单位长度地层损失占单位长度盾构体积的百分比;R 为盾构机半径。
最新Peck法计算的盾构隧道地面沉降量及沉陷槽计算公式教学提纲
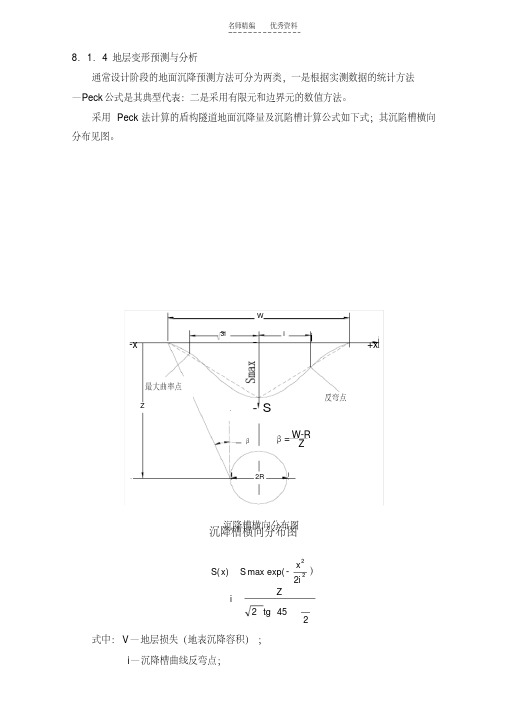
8.1.4 地层变形预测与分析通常设计阶段的地面沉降预测方法可分为两类,一是根据实测数据的统计方法—Peck 公式是其典型代表:二是采用有限元和边界元的数值方法。
采用Peck 法计算的盾构隧道地面沉降量及沉陷槽计算公式如下式;其沉陷槽横向分布见图。
沉降槽横向分布图exp(max )(S x S -222i x )2452tg Z i 式中:V —地层损失(地表沉降容积);i —沉降槽曲线反弯点;W-R β=—— 沉降槽横向分布图i W Z β2R 最大曲率点-x S 3i Z 反弯点+xz—隧道中心埋深根据本标段的地质条件和埋深等,得i=6.9m,由此根据以往的工程实践及经验公式,沉陷槽宽度B≈5i,可得单个隧道盾构推进引起的地表横向沉陷槽宽度约为35m,两座隧道盾构推进引起的地表横向沉陷曲线叠加后其沉陷槽宽度约为50m,并且沉陷槽的主要范围在隧道轴线两侧6m范围内,离轴线3m的沉降量约为最大沉降量的60%~70%,离轴线6m的沉降量约为最大沉降量的25%。
地层损失V值主要是由盾尾空隙引起的土体损失量,它与盾构机盾壳厚度、盾构推进时粘附在盾构上的土体厚度及注浆量等有关,即V=V尾+V粘-V浆盾构推进时粘附在盾构钢板上的土体厚度约为20~40mm,盾壳厚度为70mm,则:V=V尾+V粘-V浆=1.36+0.58α-(1.36+0.58)βα为折减系数,β为同步注浆的充填系数。
取α=0.6 β=0.5 得V=0.73m2由此可得地表最大沉陷值:Smax=23.4mm最大斜率:Qmax=0.0013以上分析值主要是在以往工程经验基础上结合本地铁盾构标段的实际情况,隧道埋深16m左右情况下得出的,最大沉降量满足规范和标书要求。
虽然地表沉降形态是大体相同或相似的,但其最大沉降量总是随着施工工况和地质条件的改变而千差万别,目前控制沉降的主要手段是同步注浆和二次注浆,而注浆的环节常有各种各样的问题发生,如缺量、过量、滞后、漏浆等等,不同的沉降情况常是施工工况和工作状态的反映,同时不同的地质条件沉降亦有所不同,如粉砂土较粘土隆降起量要少,沉降速率要快,淤泥质粘土后期固结沉降则要大点。
考虑注浆与超挖效应的盾构施工地表沉降计算方法

240考虑注浆与超挖效应的 盾构施工地表沉降计算方法Kao lü zhu jiang yu chao wa xiao ying dedun gou shi gong di biao chen jiang ji suan fang fa韩清盾构施工不可避免地产生地层损失继而导致地表沉降,施工中往往可以通过及时的注浆来弥补这部分损失。
通过对盾构全过程的机理分析,将地表沉降分为由于浆液流失、体积收缩导致的瞬时沉降和前方刀盘“潜在”超挖导致的固结沉降。
考虑土质情况、刀盘尺寸和浆液种类等因素的影响,提出了量化浆液向周围地层扩散效应的浆液扩散损失系数和土体由于卸荷效应而“流入”刀盘的刀盘超挖系数,并结合现场实测数据反算得到该系数取值范围。
在此基础之上,考虑注浆量、浆液配比、刀盘尺寸等因素的影响,修正了现有盾构施工引起地表沉降计算方法,通过现场实测数据验证了该修正方法的准确性,并系统分析了浆液扩散损失系数和刀盘超挖系数对沉降的影响。
研究表明:修正后计算方法能够较为准确计算地表沉降量;浆液扩散损失系数的取值范围在0.6~0.7,刀盘超挖系数的取值范围在0-0.2,浆液扩散损失系数越小,刀盘超挖系数越大,则地表越有可能发生沉降。
城市地铁施工常常采用盾构法进行掘进,然而盾构法施工会引起地表沉降,对周围建筑物产生严重危害。
因此,准确预测盾构施工引起的地表沉降对于地铁施工及周边环境稳定控制具有重要的指导意义。
目前,已有学者对该问题进行了深入的研究。
在理论研究方面,C. Sagaseta 等将隧道开挖引起的地层损失问题简化为弹性半空间问题,推导出了地层变形的解析解;张庆贺等分析了盾构施工引起的土体扰动机理;魏纲等采用弹性力学中的Mindlin 解推导了盾构施工沉降变形公式。
在数值方法方面,孙钧等采用粘弹性流变方法对盾构施工的地表沉降问题进行了数值模拟;张印涛等建立三维数值模型模拟了盾构施工地表沉降的全过程;孙玉永等通过数值模拟方法得到了隧道上方不同深度处土层的沉降槽曲线;刘波、马紫娟采用有限差分方法分析了盾构施工引起地表沉降的变化规律;在经验公式方面,Peck 通过大量的隧道施工实测沉降数据提出了沉降槽计算公式。
盾构隧道施工地表沉降监测与Peck公式变形预测分析

( , ,…, ) [( ) ] () I an a1
m
∑ an =
ρi s xi - yi 2
5
则该方法为最小二乘逼i=近0 法,由该方法得到拟合
曲线 y = s(x),该方法被称为曲线拟合最小二乘法。
式中 求取
II(最an小,a值1,,…只,需an对)为多a元n,函a1数,…I ,求a取n 的极多值元,则函有数:,若
SONG Xinhai
( , , ) China Railway 19th Bureau Group Fifth Engineering Co Ltd. Dalian Liaoning 116000 China
: ’ , Abstract On the basis of a city s underground comprehensive pipe gallery project the monitoring points around the pipe
Smax
+
1 i2
×
- x2 2
12
将 ln S(x)和 - x2 设为回归变量进行回归分析, 2
设
ln
Smax
为回归后的常数项,设
1 i2
为回归后的线性
系数,可得回归方程:
( ) ( ) ( ) ∑ ∑ Sxx =
- x2i 2 - 1
2
n
x2i 2 2
13
[( ) ( )] ( ) ( ) ∑ ∑ ∑ Sxy =
特点,但盾构法施工对岩土体形成扰动,尤其对于
周围土体的沉降影响较大。目前国内外通常使用
经验公式法[2 -3]、数值分析法[4]、模型试验法[5 - 及6]
神经网络法[7 - 8]对盾构施工沉降进行预测[9]。段绍
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
8.1.4 地层变形预测与分析
通常设计阶段的地面沉降预测方法可分为两类,一是根据实测数据的统计方法—Peck 公式是其典型代表:二是采用有限元和边界元的数值方法。
采用Peck 法计算的盾构隧道地面沉降量及沉陷槽计算公式如下式;其沉陷槽横向分布见图。
沉降槽横向分布图
exp(max )(S x S =-22
2i x )
⎪
⎭⎫ ⎝
⎛
Φ-︒=2452tg Z
i π
式中:V —地层损失(地表沉降容积);
W-R β=—— 沉降槽横向分布图
i
W
Z
β
2R 最大曲率点
-x S
3i
Z
反弯点
+x
i—沉降槽曲线反弯点;
z—隧道中心埋深
根据本标段的地质条件和埋深等,得i=6.9m,由此根据以往的工程实践及经验公式,沉陷槽宽度B≈5i,可得单个隧道盾构推进引起的地表横向沉陷槽宽度约为35m,两座隧道盾构推进引起的地表横向沉陷曲线叠加后其沉陷槽宽度约为50m,并且沉陷槽的主要范围在隧道轴线两侧6m范围内,离轴线3m的沉降量约为最大沉降量的60%~70%,离轴线6m的沉降量约为最大沉降量的25%。
地层损失V值主要是由盾尾空隙引起的土体损失量,它与盾构机盾壳厚度、盾构推进时粘附在盾构上的土体厚度及注浆量等有关,即
V=V尾+V粘-V浆
盾构推进时粘附在盾构钢板上的土体厚度约为20~40mm,盾壳厚度为70mm,则:V=V尾+V粘-V浆=1.36+0.58α-(1.36+0.58)β
α为折减系数,
β为同步注浆的充填系数。
取α=0.6 β=0.5 得V=0.73m2
由此可得地表最大沉陷值:Smax=23.4mm
最大斜率:Qmax=0.0013
以上分析值主要是在以往工程经验基础上结合本地铁盾构标段的实际情况,隧道埋深16m左右情况下得出的,最大沉降量满足规范和标书要求。
虽然地表沉降形态是大体相同或相似的,但其最大沉降量总是随着施工工况和地质条件的改变而千差万别,目前控制沉降的主要手段是同步注浆和二次注浆,而注浆的环节常有各种各样的问题发生,如缺量、过量、滞后、漏浆等等,不同的沉降情况常是施工工况和工作状态的反映,同时不同的地质条件沉降亦有所不同,如粉砂土较粘土隆降起量要少,沉降速率要快,淤泥质粘土后期固结沉降则要大点。
以上这些都要求盾构施工时要加强监测工作,以随时了解地面沉降信息,以便及时采取有效措施,以达到控制沉降和减少损失的目的。
8.2 理论分析
施工引起的地面沉降和围岩变形,理论分析通过地层—结构模型模拟计算,本次计算采用有限元单元法,利用2D-σ计算程序模拟计算。
8.2.1 计算模型
因隧道是一个狭长的建筑物,纵向很长,横向相对尺寸较小。
隧道计算可以取中间每延米隧道,作为平面应变问题来近似处理。
隧道模拟计算模型采用平面应变模型,计算范围上取至地面,下部和横向取隧道洞径的5倍左右为计算域。
计算采用2D-σ程序进行模拟计算分析。
计算结构模型和单元网格图如下图所示。
计算工况选取区间DK19+700.000地段, 隧道埋深16.7m ,区间盾构穿越的地层为
中、粗砂层及圆砾层。
M
M
M M
M M
M
M
M
M Fσ=120.000000Fσ=120.000000Fσ=120.000000
8.2.2 屈服准则
有限元法用于求解岩土工程问题主要有两点特殊的地方,一是采用的破坏准则不同,一是对施工过程的模拟。
对岩土工程材料,可以近似看作Mohr ——Coulomb 体,因此在计算中采用主应力空间下的Mohr ——Coulomb 屈服准则:
τσφf n c tg =+
(a )
其物理意义是,当岩土体中一点在某个面上的剪应力达到c+σntg φ时,该点将发生剪切破坏。
用主应力表示,则可写为
()cos ()sin σσσσφ13132-=⋅++c (b )
在编制程序时,为与其它屈服准则统一起来,可将它以不变量的形式表示出来,即
cos sin sin 3
cos sin 32=⋅--
+=ϕθϕθφσc J J F m
(c )
σm ——三个正应力的平均值;
J2、J3——应力偏量的第二、第三不变量。
8.2.3 有限元数值分析结果
最终变形状态见下“位移网格图”,最大沉降量为11.mm,双洞施工后沉降槽宽度为42m,沉降槽曲线最大坡度为1.14‰。
8.3 控制地层变形保护建筑物的措施
根据投标书的要求,沉降量一般控制在+10/-30mm之间,施工中可采取以下措施。
1)盾构前方的隆陷控制
地表隆起的主要原因是盾构正面对土体的推应力大于原始侧向地应力,因此在实时监测的情况下可以根据地表隆起状况调整推进速度及出土量,降低正面土仓压力达到降低地表隆起的目的。
地表沉降过大则是由于开挖面推力小于原始应力而引起的,应通过调整推进速度及减少出土量,提高正面土仓压力方式来控制沉降。
2)盾构通过时的沉降控制
这一沉降是无法避免的,但是如果沉降超限可以采取控制掘进速度和出土量,调整土仓压力,控制同步注浆的压力及注浆量,从而达到有效控制地层的弹塑性变形。
保持盾构开挖面的稳定,防止地层失水。
主要通过掘进速度和出土量等参数的控制,保证工作面的合适压力,施工中要避免地层失水,尤其在断层破碎带应通过向工作面加注澎闰土浆或泡沫保持好土压平衡,防止在敞开、半敞开状态下出现涌水突泥发生,必要时可加气压施工。
3)固结沉降的控制
盾构通过后,由于应力松弛影响,地层还会发生固结沉降,为此应根据地面实时监测结果进行实时控制,在管片衬砌背后实施二次注浆,尤其对拱部120°范围进行地层固结注浆是非常重要的。
主要控制参数为注浆量和注浆压力。
二次(或多次)压浆是弥补同步注浆不足,减少地表沉降的有效辅助手段,可使盾构在穿越建筑物、道路、地下管线时,大大降低地面沉降。
4)信息化管理
本标段区间隧道穿越地上建筑物较复杂,建筑物的基础型式、埋深等情况无具体资料。
为保证地面建筑物的安全,如我单位中标后将对沿线建筑物基础进行深入调查,避免工程的不可预见性。
在建筑物设置系统的观测网,进行变形监测并及时反馈信息,作到信息化施工。
根据建筑物的结构类型及对沉降的敏感程度、沉降的允许值,制定建筑物及地面变形警界值。
根据反馈信息,及时进行跟踪注浆或补充注浆。
5)其它措施
盾构在曲线推进、纠偏、抬头或叩头推进过程中,实际开挖断面不是圆形而是椭圆,从而会引起附加变形,此时应调整掘进速度与正面土压,达到减少对地层的扰动度和减少超挖的效果,从而减少地层的变形。
盾构暂停推进时,可能会引起盾构后退,而使开挖面松弛造成地表沉陷,此时应作好防止盾构后退措施,并对开挖面及盾尾采取封闭措施。
加强机械检修养护,建筑物下进行快速匀速掘进。
防止螺旋输送机喷涌砂,盾尾和铰接部位漏砂等,造成地层损失,加大沉降。
在曲线地段施工时,减少超挖。
