2018届高考数学立体几何(理科)专题02 二面角

合集下载

高中数学必修2立体几何专题二面角典型例题解法总结(最新整理)

AA 1 =2, E、E 1 、F 分别是棱 AD、AA 1 、AB 的中点。
D1
A1 （1）证明：直线 EE 1 //平面 FCC 1 ；
C1 B1
（2）求二面角 B-FC 1 -C 的余弦值。
E1
D
E
A
F
C B
证（1）略解（ 2）因为 AB=4, BC=CD=2, 、 F 是棱 AB 的中点 ,所以 A1 BF=BC=CF,△BCF 为正三角形,取 CF 的中点 O,则 OB⊥CF,又因
分析：本题是一道典型的利用三垂线定理求二面角问题，在证明 AD⊥平面 PAB 后，容易发现平面 PAB⊥ 平面 ABCD，点 P 就是二面角 P-BD-A 的半平面上的一个点，于是可过点 P 作棱 BD 的垂线，再作平面 ABCD
的垂线，于是可形成三垂线定理中的斜线与射影内容，从而可得本解法。（答案：二面角 P BD A 的大
2 ，则 GF
2
，
2
又∵ SA AC 6 ，∴ AM 2 ，∵ AM AB 2 ， ABM 600 ∴△ ABM 是等边三角形，∴
BF 3 。在△ GAB 中， AG 6 ， AB 2 ， GAB 900 ，∴ BG 3 4 11
2
2
2
cos BFG GF 2 FB 2 BG 2
6
，求二面角 E—AF—C 的余弦值.
2
分析：第 1 题容易发现，可通过证 AE⊥AD 后推出 AE⊥平面 APD，使命题获证，而第 2 题，则首先必须在找到最大角正切值有关的线段计算出各线段的长度之后，考虑到运用在二面角的棱 AF 上找到可计算二面角的平面角的顶点 S，和两边 SE 与 SC，进而计算二面角的余弦值。（答

届高考数学立体几何理科专题二面角

2018届高考数学立体几何（理科）专题02 二面角1．如图，在三棱柱111ABC A B C -中， 1,90A A AB ABC =∠=︒侧面11A ABB ⊥底面ABC . (1)求证： 1AB ⊥平面1A BC ；(2)若15360AC BC A AB ==∠=︒，，,求二面角11B A C C --的余弦值.2．如图所示的多面体中，下底面平行四边形与上底面平行，且，,，，平面平面，点为的中点．（1）过点作一个平面与平面平行，并说明理由；（2）求平面与平面所成锐二面角的余弦值．3．如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形， 2AB AD =， 3BD =，且PD ⊥底面ABCD . （1）证明：平面PBD ⊥平面PBC ；（2）若Q 为PC 的中点，且1AP BQ ⋅=u u u v u u u v，求二面角Q BD C --的大小.4．如图所示的几何体是由棱台和棱锥拼接而成的组合体，其底面四边形是边长为2的菱形，，平面. （1）求证：；（2）求平面与平面所成锐角二面角的余弦值.5．在四棱锥P ABCD -中，四边形ABCD 是矩形，平面PAB ⊥平面ABCD ，点E 、F 分别为BC 、AP 中点.（1）求证： //EF 平面PCD ；（2）若0,120,AD AP PB APB ==∠=，求平面DEF 与平面PAB 所成锐二面角的余弦值.6．如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形, ,90AD BC ADC ∠=oP ,平面PAD ⊥底面ABCD ,Q 为AD 中点, M 是棱PC 上的点, 12,1,2PA PD BC AD CD =====（Ⅰ）若点M 是棱PC 的中点,求证: PA P 平面BMQ ; （Ⅱ）求证:平面PQB ⊥平面PAD ;（Ⅲ）若二面角M BQ C --为30o,设PM tMC =,试确定t 的值.2018届高考数学立体几何（理科）专题02 二面角（教师版）1．如图，在三棱柱111ABC A B C -中， 1,90A A AB ABC =∠=︒侧面11A ABB ⊥底面ABC . (1)求证： 1AB ⊥平面1A BC ；(2)若15360AC BC A AB ==∠=︒，，,求二面角11B A C C --的余弦值.【答案】（1）证明见解析；（2）2114-.Q 侧面11A ABB ⊥底面,90ABC ABC ∠=︒，CB ∴⊥侧面11A ABB ，1CB AB ∴⊥.又1A B BC B ⋂=Q ,1AB ∴⊥平面1A BC .(2)在Rt ABC n 中， 5,3,4AC BC AB ==∴=,又菱形11A ABB 中， 160A AB ∠=︒Q ，1A AB ∴n 为正三角形.设(),,n x y z =为平面11A CC 的方向量，则1110,2230,{ { 0.22330.n C C x y n C A x y z =-+=∴=+-=u u u u r u u u u rn n 令3x =,得()n 3,3,4=为平面11A CC 的一个法向量.又()10,23,0OB =-u u u r为平面1A BC 的一个法向量，11121cos , 142723n OB n OB n OB ===-n n n u u u ru u u r u u u r .∴二面角11B A C C --的余弦值为21-. 2．如图所示的多面体中，下底面平行四边形与上底面平行，且，,，，平面平面，点为的中点．（1）过点作一个平面与平面平行，并说明理由；（2）求平面与平面所成锐二面角的余弦值．【答案】（1）见解析；（2）试题解析：（1）取的中点，的中点，连接、、，如图所示．则平面平面，平面即为所求的平面．理由如下：在平行四边形中，点分别是与的中点，所以，在中，点分别是的中点，所以．显然，，所以平面平面，亦即平面平面．（2）不妨设,,，故,．在平行四边形中，，所以．取的中点，则．又平面平面，平面平面，所以平面．连接，因为，，所以，又，所以．如图所示，以点为坐标原点建立空间直角坐标系，则，，，，，，,，．所以，，，．设平面的法向量为，则由，即，整理得．令，．所以．所以．3．如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形， 2AB AD =， 3BD AD =，且PD ⊥底面ABCD . （1）证明：平面PBD ⊥平面PBC ；（2）若Q 为PC 的中点，且1AP BQ ⋅=u u u v u u u v，求二面角Q BD C --的大小. 【答案】（1）见解析（2）4π试题解析：（1）证明：∵222AD BD AB +=，∴AD BD ⊥，∴//AD BC ，∴BC BD ⊥. 又∵PD ⊥底面ABCD ，∴PD BC ⊥.∵PD BD D ⋂=，∴BC ⊥平面PBD . 而BC ⊂平面PBC ，∴平面PBC ⊥平面PBD . （2）解：由（1）知， BC ⊥平面PBD ，∴2112tAP BQ+⋅==u u u v u u u v，∴1t=.故131,,222DQ⎛⎫=-⎪⎪⎝⎭u u u v，131,,222BQ⎛⎫=--⎪⎪⎝⎭u u u v.设平面QBD 的法向量为(),,n x y z=v，则{n DQn BQ⋅=⋅=u u u vvu u u vv，即131222{13122x y zx y z-++=--+=，令1x=，得()1,0,1n=v. 易知平面BDC的一个法向量为()0,0,1m=v，则2cos,221m n==⨯v v，∴二面角Q BD C--的大小为4π. 4．如图所示的几何体是由棱台和棱锥拼接而成的组合体，其底面四边形是边长为2的菱形，，平面.（1）求证：；（2）求平面与平面所成锐角二面角的余弦值.【答案】（1）证明见解析；（2）.又棱台中，∴(2)建立空间直角坐标系如图所示，则，，，，，，所以，，，，设平面的一个法向量为，则,∴，.令，得， ∴；设平面的法向量为，则,∴，令，得，， ∴，设平面与平面所成锐二面角为，则，所以平面与平面所成锐二面角的余弦值为.5．在四棱锥P ABCD -中，四边形ABCD 是矩形，平面PAB ⊥平面ABCD ，点E 、F 分别为BC 、AP 中点.（1）求证： //EF 平面PCD ；（2）若0,120,AD AP PB APB ==∠=，求平面DEF 与平面PAB 所成锐二面角的余弦值.【答案】（1）见解析（2）3020试题解析：（I ）证明：取PD 中点G ，连接,GF GC ．在△PAD 中，有 ,G F 分别为PD 、AP 中点∴ 1//2GF AD而GC ⊂平面PCD ， EF ⊄平面PCD ∴ //EF 平面PCD（II ）取AB 中点O ，连接OP ，设=2AD . Q 四边形ABCD 是矩形∴ AD AB ⊥Q 平面PAB ⊥平面ABCD ,平面PAB ⋂平面ABCD = AB ， AD ⊂平面PAB∴ AD ⊥平面PAB 又 AD AP PB ==， 0=120APB ∠， O 为AB中点∴ OP AB ⊥， 3OA OB ==， 1OP =.故可建立空间直角坐标系O xyz -，如图所示，则300A （，，）， 010P （，，）， 300B -（，，）， ()3,0,2C -， ()3,0,2D ∴ 31,,022F ⎛⎫ ⎪ ⎪⎝⎭， ()3,0,1E - ∴ ()23,0,1DE =--u u u v ， 31,,222DF ⎛⎫=-- ⎪ ⎪⎝⎭u u u v 设(),,n x y z =v 是平面DEF 的一个法向量，则·0{ ·0DE n DF n ==u u u v v u u u v v ，即230{ 312022x z x y z --=-+-=不妨设1x =，则()1,73,23n =--v ．易知向量()0,0,2AD =u u u v 为平面PAB 的一个法向量． ∴ ()()222·23230cos ,20·173232n AD n AD n AD -⨯===-+-+-⨯u u u v v u u u v v u u u v v 故平面DEF 与平面PAB 所成锐二面角的余弦值为3020. 6．如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形, ,90AD BC ADC ∠=o P ,平面PAD ⊥底面ABCD ,Q 为AD 中点, M 是棱PC 上的点, 12,1,32PA PD BC AD CD =====. （Ⅰ）若点M 是棱PC 的中点,求证: PA P 平面BMQ ;（Ⅱ）求证:平面PQB ⊥平面PAD ; （Ⅲ）若二面角M BQ C --为30o ,设PM tMC =,试确定t 的值.试题解析：因为MN ⊂平面BMQ , PA ⊄平面BMQ 所以PA P 平面BMQ .（Ⅱ）因为1,,2AD BC BC AD Q =P 为AD 中点, 所以四边形BCDQ 为平行四边形,所以CD BQ P .因为90ADC ∠=o ,所以90AQB ∠=o ,即AD BQ ⊥.又因为平面PAD ⊥平面ABCD ,且平面PAD ⋂平面ABCD AD =,所以BQ ⊥平面PAD ,因为BQ ⊂平面PQB ,所以平面PAD ⊥平面PQB .（Ⅲ）因为,PA PD Q =为AD 的中点,所以PQ AD ⊥.又因为平面PAD ⊥平面ABCD ,且平面PAD ⋂平面ABCD AD =,所以PQ ⊥平面ABCD以Q 为原点,以,QA QB u u u v u u u v 的方向分别为x 轴, y 轴的正方向,建立如图所示的空间直角坐标系Q xyz -, 则点()0,0,0Q, (P, ()B, ()C -,平面BQC 的一个法向量()0,0,1n =v. 设(),,M x y z ,则(,,,PM x y z =u u u u v,()1,MC x y z =---u u u u v ,因为PM tMC =u u u u v u u u u v 所以())()11{ { t x t x t x y t y y z t z z =-+=--=⇒-=在平面MBQ 中, (),,,111t QB QM t t t ⎛⎫==- ⎪ ⎪+++⎝⎭u u u v u u u u v , 因为二面角M BQ C --为30o ,所以cos30m n m n ⋅==⋅o v v v v ,所以3t =.。

2018年高考理科数学分类汇编---立体几何

2018年全国高考理科数学分类汇编——立体几何1.（北京）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为（C）A．1 B．2 C．3 D．4解：四棱锥的三视图对应的直观图为：PA⊥底面ABCD，AC=，CD=，PC=3，PD=2，可得三角形PCD不是直角三角形．所以侧面中有3个直角三角形，分别为：△PAB，△PBC，△PAD．故选：C．2.（北京）如图，在三棱柱ABC﹣A1B1C1中，CC1⊥平面ABC，D，E，F，G分别为AA1，AC，A1C1，BB1的中点，AB=BC=，AC=AA1=2．（Ⅰ）求证：AC⊥平面BEF；（Ⅱ）求二面角B﹣CD﹣C1的余弦值；（Ⅲ）证明：直线FG与平面BCD相交．【解答】（I）证明：∵E，F分别是AC，A1C1的中点，∴EF∥CC1，∵CC1⊥平面ABC，∴EF⊥平面ABC，又AC⊂平面ABC，∴EF⊥AC，∵AB=BC，E是AC的中点，∴BE⊥AC，又BE∩EF=E，BE⊂平面BEF，EF⊂平面BEF，∴AC⊥平面BEF．（II）解：以E为原点，以EB，EC，EF为坐标轴建立空间直角坐标系如图所示：则B（2，0，0），C（0，1，0），D（0，﹣1，1），∴=（﹣2，1，0），=（0，﹣2，1），设平面BCD的法向量为=（x，y，z），则，即，令y=2可得=（1，2，4），又EB⊥平面ACC1A1，∴=（2，0，0）为平面CD﹣C1的一个法向量，∴cos＜，＞===．由图形可知二面角B﹣CD﹣C1为钝二面角，∴二面角B﹣CD﹣C1的余弦值为﹣．（III）证明：F（0，0，2），（2，0，1），∴=（2，0，﹣1），∴•=2+0﹣4=﹣2≠0，∴与不垂直，∴FG与平面BCD不平行，又FG⊄平面BCD，∴FG与平面BCD相交．3.（江苏）如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为．【解答】解：正方体的棱长为2，中间四边形的边长为：，八面体看做两个正四棱锥，棱锥的高为1，多面体的中心为顶点的多面体的体积为：2×=．故答案为：．4.（江苏）在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，AB1⊥B1C1．求证：（1）AB∥平面A1B1C；（2）平面ABB1A1⊥平面A1BC．【解答】证明：（1）平行六面体ABCD﹣A1B1C1D1中，AB∥A1B1，⇒AB∥平面A1B1C；（2）在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，⇒四边形ABB1A1是菱形，⊥AB1⊥A1B．在平行六面体ABCD﹣A1B1C1D1中，AA1=AB，AB1⊥B1C1⇒AB1⊥BC．∴⇒AB1⊥面A1BC，且AB1⊂平面ABB1A1⇒平面ABB1A1⊥平面A1BC．5.（全国1卷）某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）BA．2B．2C．3 D．2【解答】解：由题意可知几何体是圆柱，底面周长16，高为：2，直观图以及侧面展开图如图：圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度：=2．故选：B．6.（全国1卷）已知正方体的棱长为1，每条棱所在直线与平面α所成的角都相等，则α截此正方体所得截面面积的最大值为（）AA．B．C．D．【解答】解：正方体的所有棱中，实际上是3组平行的棱，每条棱所在直线与平面α所成的角都相等，如图：所示的正六边形平行的平面，并且正六边形时，α截此正方体所得截面面积的最大，此时正六边形的边长明明就的最大值为：6×=．故选：A．7.（全国1卷）如图，四边形ABCD为正方形，E，F分别为AD，BC的中点，以DF为折痕把△DFC折起，使点C到达点P的位置，且PF⊥BF．（1）证明：平面PEF⊥平面ABFD；（2）求DP与平面ABFD所成角的正弦值．【解答】（1）证明：由题意，点E、F分别是AD、BC的中点，则，，由于四边形ABCD为正方形，所以EF⊥BC．由于PF⊥BF，EF∩PF=F，则BF⊥平面PEF．又因为BF⊂平面ABFD，所以：平面PEF⊥平面ABFD．（2）在平面DEF中，过P作PH⊥EF于点H，联结DH，由于EF为面ABCD和面PEF的交线，PH⊥EF，则PH⊥面ABFD，故PH⊥DH．在三棱锥P﹣DEF中，可以利用等体积法求PH，因为DE∥BF且PF⊥BF，所以PF⊥DE，又因为△PDF≌△CDF，所以∠FPD=∠FCD=90°，=，所以PF⊥PD，由于DE∩PD=D，则PF⊥平面PDE，故V F﹣PDE因为BF∥DA且BF⊥面PEF，所以DA⊥面PEF，所以DE⊥EP．设正方形边长为2a，则PD=2a，DE=a，在△PDE中，，所以，故V F﹣PDE=，又因为，所以PH==，所以在△PHD中，sin∠PDH==，即∠PDH为DP与平面ABFD所成角的正弦值为：．8.（全国2卷）在长方体ABCD﹣A1B1C1D1中，AB=BC=1，AA1=，则异面直线AD1与DB1所成角的余弦值为（）CA．B．C．D．【解答】解：以D为原点，DA为x轴，DC为y轴，DD1为z轴，建立空间直角坐标系，∵在长方体ABCD﹣A1B1C1D1中，AB=BC=1，AA1=，∴A（1，0，0），D1（0，0，），D（0，0，0），B1（1，1，），=（﹣1，0，），=（1，1，），设异面直线AD1与DB1所成角为θ，则cosθ===，∴异面直线AD1与DB1所成角的余弦值为．故选：C．9.（全国2卷）如图，在三棱锥P﹣ABC中，AB=BC=2，PA=PB=PC=AC=4，O为AC的中点．（1）证明：PO⊥平面ABC；（2）若点M在棱BC上，且二面角M﹣PA﹣C为30°，求PC与平面PAM所成角的正弦值．【解答】解：（1）证明：∵AB=BC=2，O是AC的中点，∴BO⊥AC，且BO=2，又PA=PC=PB=AC=2，∴PO⊥AC，PO=2，则PB2=PO2+BO2，则PO⊥OB，∵OB∩AC=O，∴PO⊥平面ABC；（2）建立以O坐标原点，OB，OC，OP分别为x，y，z轴的空间直角坐标系如图：A（0，﹣2，0），P（0，0，2），C（0，2，0），B（2，0，0），=（﹣2，2，0），设=λ=（﹣2λ，2λ，0），0＜λ＜1则=﹣=（﹣2λ，2λ，0）﹣（﹣2，﹣2，0）=（2﹣2λ，2λ+2，0），则平面PAC的法向量为=（1，0，0），设平面MPA的法向量为=（x，y，z），则=（0，﹣2，﹣2），则•=﹣2y﹣2z=0，•=（2﹣2λ）x+（2λ+2）y=0令z=1，则y=﹣，x=，即=（，﹣，1），∵二面角M﹣PA﹣C为30°，∴cos30°=|=，即=，解得λ=或λ=3（舍），则平面MPA的法向量=（2，﹣，1），=（0，2，﹣2），PC与平面PAM所成角的正弦值sinθ=|cos＜，＞|=||==．10.（全国3卷）中国古建筑借助榫卯将木构件连接起来．构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是（）AA．B．C．D．【解答】解：由题意可知，如图摆放的木构件与某一带卯眼的木构件咬合成长方体，小的长方体，是榫头，从图形看出，轮廓是长方形，内含一个长方形，并且一条边重合，另外3边是虚线，所以木构件的俯视图是A．故选：A．11.（全国3卷）设A，B，C，D是同一个半径为4的球的球面上四点，△ABC为等边三角形且面积为9，则三棱锥D﹣ABC体积的最大值为（）BA．12B．18C．24D．54【解答】解：△ABC为等边三角形且面积为9，可得，解得AB=6，球心为O，三角形ABC 的外心为O′，显然D在O′O的延长线与球的交点如图：O′C==，OO′==2，则三棱锥D﹣ABC高的最大值为：6，则三棱锥D﹣ABC体积的最大值为：=18．故选：B．12.（全国3卷）如图，边长为2的正方形ABCD所在的平面与半圆弧所在平面垂直，M是上异于C，D的点．（1）证明：平面AMD⊥平面BMC；（2）当三棱锥M﹣ABC体积最大时，求面MAB与面MCD所成二面角的正弦值．【解答】解：（1）证明：在半圆中，DM⊥MC，∵正方形ABCD所在的平面与半圆弧所在平面垂直，∴AD⊥平面BCM，则AD⊥MC，∵AD∩DM=D，∴MC⊥平面ADM，∵MC⊂平面MBC，∴平面AMD⊥平面BMC．（2）∵△ABC的面积为定值，∴要使三棱锥M﹣ABC体积最大，则三棱锥的高最大，此时M为圆弧的中点，建立以O为坐标原点，如图所示的空间直角坐标系如图∵正方形ABCD的边长为2，∴A（2，﹣1，0），B（2，1，0），M（0，0，1），则平面MCD的法向量=（1，0，0），设平面MAB的法向量为=（x，y，z）则=（0，2，0），=（﹣2，1，1），由•=2y=0，•=﹣2x+y+z=0，令x=1，则y=0，z=2，即=（1，0，2），则cos＜，＞===，则面MAB与面MCD所成二面角的正弦值sinα==．13.（上海）《九章算术》中，称底面为矩形而有一侧棱垂直于底面的四棱锥为阳马，设AA1是正六棱柱的一条侧棱，如图，若阳马以该正六棱柱的顶点为顶点、以AA1为底面矩形的一边，则这样的阳马的个数是（）CA．4 B．8 C．12 D．16【解答】解：根据正六边形的性质可得D1F1⊥A1F1，C1A1⊥A1F1，D1B1⊥A1B1，E1A1⊥A1B1，则D1﹣A1ABB1，D1﹣A1AFF1满足题意，而C1，E1，C，D，E和D1一样，故有2×6=12，故选：C．14.（上海）已知圆锥的顶点为P，底面圆心为O，半径为2．（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO=4，OA、OB是底面半径，且∠AOB=90°，M为线段AB的中点，如图．求异面直线PM与OB所成的角的大小．【解答】解：（1）∵圆锥的顶点为P，底面圆心为O，半径为2，圆锥的母线长为4，∴圆锥的体积V===．（2）∵PO=4，OA，OB是底面半径，且∠AOB=90°，M为线段AB的中点，∴以O为原点，OA为x轴，OB为y轴，OP为z轴，建立空间直角坐标系，P（0，0，4），A（2，0，0），B（0，2，0），M（1，1，0），O（0，0，0），=（1，1，﹣4），=（0，2，0），设异面直线PM与OB所成的角为θ，则cosθ===．∴θ=arccos．∴异面直线PM与OB所成的角的为arccos．15. （天津）已知正方体ABCD﹣A1B1C1D1的棱长为1，除面ABCD外，该正方体其余各面的中心分别为点E，F，G，H，M（如图），则四棱锥M﹣EFGH的体积为．【解答】解：正方体的棱长为1，M﹣EFGH的底面是正方形的边长为：，四棱锥是正四棱锥，棱锥的高为，四棱锥M﹣EFGH的体积：=．故答案为：．16.（天津）如图，AD∥BC且AD=2BC，AD⊥CD，EG∥AD且EG=AD，CD∥FG且CD=2FG，DG⊥平面ABCD，DA=DC=DG=2．（Ⅰ）若M为CF的中点，N为EG的中点，求证：MN∥平面CDE；（Ⅱ）求二面角E﹣BC﹣F的正弦值；（Ⅲ）若点P在线段DG上，且直线BP与平面ADGE所成的角为60°，求线段DP的长．【解答】（Ⅰ）证明：依题意，以D为坐标原点，分别以、、的方向为x轴，y轴，z轴的正方向建立空间直角坐标系．可得D（0，0，0），A（2，0，0），B（1，2，0），C（0，2，0），E（2，0，2），F（0，1，2），G（0，0，2），M（0，，1），N（1，0，2）．设为平面CDE的法向量，则，不妨令z=﹣1，可得；又，可得．又∵直线MN⊄平面CDE，∴MN∥平面CDE；（Ⅱ）解：依题意，可得，，．设为平面BCE的法向量，则，不妨令z=1，可得．设为平面BCF的法向量，则，不妨令z=1，可得．因此有cos＜＞=，于是sin＜＞=．∴二面角E﹣BC﹣F的正弦值为；（Ⅲ）解：设线段DP的长为h，（h∈[0，2]），则点P的坐标为（0，0，h），可得，而为平面ADGE的一个法向量，故|cos＜＞|=．由题意，可得，解得h=∈[0，2]．∴线段DP的长为．17.（浙江）某几何体的三视图如图所示（单位：cm），则该几何体的体积（单位：cm3）是（）CA．2 B．4 C．6 D．8【解答】解：根据三视图：该几何体为底面为直角梯形的四棱柱．如图所示：故该几何体的体积为：V=．故选：C．18.（浙江）已知平面α，直线m，n满足m⊄α，n⊂α，则“m∥n”是“m∥α”的（）AA．充分不必要条件 B．必要不充分条件C．充分必要条件D．既不充分也不必要条件【解答】解：∵m⊄α，n⊂α，∴当m∥n时，m∥α成立，即充分性成立，当m∥α时，m∥n不一定成立，即必要性不成立，则“m∥n”是“m∥α”的充分不必要条件．故选：A．19.(浙江) 已知四棱锥S﹣ABCD的底面是正方形，侧棱长均相等，E是线段AB上的点（不含端点）．设SE与BC所成的角为θ1，SE与平面ABCD所成的角为θ2，二面角S﹣AB﹣C的平面角为θ3，则（）DA．θ1≤θ2≤θ3B．θ3≤θ2≤θ1C．θ1≤θ3≤θ2D．θ2≤θ3≤θ1【解答】解：∵由题意可知S在底面ABCD的射影为正方形ABCD的中心．过E作EF∥BC，交CD于F，过底面ABCD的中心O作ON⊥EF交EF于N，连接SN，取CD中点M，连接SM，OM，OE，则EN=OM，则θ1=∠SEN，θ2=∠SEO，θ3=∠SMO．显然，θ1，θ2，θ3均为锐角．∵tanθ1==，tanθ3=，SN≥SO，∴θ1≥θ3，又sinθ3=，sinθ2=，SE≥SM，∴θ3≥θ2．故选：D．20.（浙江）如图，已知多面体ABCA1B1C1，A1A，B1B，C1C均垂直于平面ABC，∠ABC=120°，A1A=4，C1C=l，AB=BC=B1B=2．（Ⅰ）证明：AB1⊥平面A1B1C1；（Ⅱ）求直线AC1与平面ABB1所成的角的正弦值．【解答】（I）证明：∵A1A⊥平面ABC，B1B⊥平面ABC，∴AA1∥BB1，∵AA1=4，BB1=2，AB=2，∴A1B1==2，又AB1==2，∴AA12=AB12+A1B12，∴AB1⊥A1B1，同理可得：AB1⊥B1C1，又A1B1∩B1C1=B1，∴AB1⊥平面A1B1C1．（II）解：取AC中点O，过O作平面ABC的垂线OD，交A1C1于D，∵AB=BC，∴OB⊥OC，∵AB=BC=2，∠BAC=120°，∴OB=1，OA=OC=，以O为原点，以OB，OC，OD所在直线为坐标轴建立空间直角坐标系如图所示：则A（0，﹣，0），B（1，0，0），B1（1，0，2），C1（0，，1），∴=（1，，0），=（0，0，2），=（0，2，1），设平面ABB1的法向量为=（x，y，z），则，∴，令y=1可得=（﹣，1，0），∴cos＜＞===．设直线AC1与平面ABB1所成的角为θ，则sinθ=|cos＜＞|=．∴直线AC1与平面ABB1所成的角的正弦值为．。

2018年全国二卷立体几何（文理）详解

2018年全国二卷立体几何（文理）详解各位铁子门，欢迎大家再次来到孙老师的鹏哥谈数学！上两节课带着大家分析了2018年全国一卷、三卷的立体几何解答题，大家有怎么样的感受？此时，你的内心有没有一点点涟漪浮起？……12分的解答题，简直是弱爆了，竟然只考……面面垂直、空间角……其实吧，所谓命题专家也就这点能耐了！……不信，你再看2018年的全国二卷之立体几何…………竟然……线面垂直、空间角……（据说葛大爷葛军退役后，江湖再无哭泣，人间宁静安详……）来看看二卷的这道题，心细的伙伴们有没有发现，我们二卷的立体几何经常考棱锥（文理科一样样），不信，你看………16年五棱锥（菱形对折）、17年四棱锥、18年三棱锥…….……额……19年要考谁？能考谁？来来来，孙老师偷偷告诉你……（哈哈，我总是低调不了，总是这么傲娇，我想总有一天会死得很惨，哈哈哈）我们先看18年二卷理科的这道题（孙老师忍不住想告诉你，18年理科这道题的题号发生了调整，干翻了解析几何老二的宝座，跑到了第20题，这是疏忽还是有意，各位童鞋们怎么看，哈哈哈！）：（1）线面垂直……我不想多做解释了，实在记不起来，回头看我的前一篇帖子2018年全国一卷理科数学立体几何详解我还是忍不住想再说一遍，老师嘛，传道受业解惑也！……如果一条直线与一个平面内的两条相交直线都垂直，那么该直线与此平面垂直……当然，我们需要先尝试找到边角关系，中点是突破口，等腰三角形是关键，勾股定理是核心，判定定理算锤子，于是乎……（2）空间角之线面角……还要再重复吗？no……你已成仙，再不晓得就自己挂掉吧！（童话里都是骗人的.......忽然想到了成龙大哥，金喜善.......年代久远，尔等可能不知道，历史人物......）建系……我们再看18年二卷文科的这道题：……立体几何，同样的三棱锥，长相神似理科，两个问题…………线面垂直、点面距……额，文科的特点来了，都说文科感性，理科理性，扯什么淡，有证据吗？我也会写诗，我也能抒情，原谅一个理工直男的表白吧！哈哈，我都说了些什么？嗯…….算了吧，不作践自己了！孙老师也是重情之人，脸皮薄，容易脸红，本来脸黑，一红就更黑了……（哈哈哈）点面距…..？什么东西？……垂线上任意一点到垂足间的线段，叫做这个点到这个平面的垂线段．垂线段的长度叫做这个点到平面的距离!那么，我们怎么解决点面距的问题？（三个方法，随便你爱那个，只要能放电就行！）（1）找点投影法求点面距（告诉你，这个基本帮不了什么你忙，所以，别多想……）（2）等体积法求点面距（学马克思的小伙伴们，注意啦！这个是需要你记住的，重要的事情孙老师历来只说一遍，这次孙老师说三遍三遍啊，什么概念？不想死就必须记下！）（3）空间向量法求点面距（哈哈哈，文科生不太能理解，专属理科生，万能的！重要性你懂得！）我们看这道题：（1）线面垂直……（2）点面距……等体积法（文科嘛！也只能这样了，局限性……）。

【2018新课标高考必考知识点教学计划教学安排教案设计】高二数学：二面角的常见求法

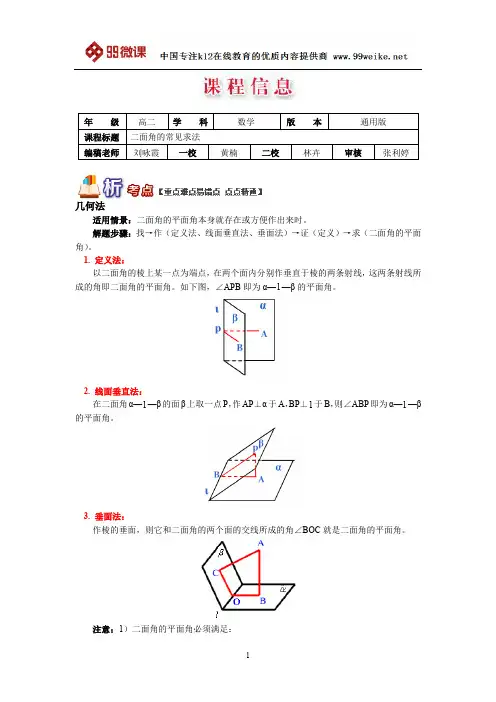
y1 x1 y2 x2 n MA 0 n MB 0 和，解得有 1 和 2 z 2 x n MC 0 n MC 0 1 1 z2 2 x2 1 2
AD平面 M，设 AHD＝是二面角 A－BC－D 的平面角，由 cos ＝
AD 可得， AH
ABC 与它在过其底边 BC 的平面 M 上的射影 DBC 以及两者所成的二面角之间的关系：
S cos SDBC 射。 SABC S
向量法
适用情景：二面角的平面角不易作出来时。解题步骤：建立空间直角坐标系→求出两个平面的法向量 m, n →代入公式。注意： 1. 若二面角为锐二面角，则 cos
1 图所示空间直角坐标系，则 A(0， 0，， 0) B(0， 2，， 0) C (11 ，，， 0) D(11 ，，， 0) P(0， 0，， 1) M 0， 1 ，。 2
DC AP 0, 即 DC AP ，又由已知 DC AD 且 AP AD A ，从而 DC 面PAD ，又 DC 面PCD ，故面 PAD 面 PCD 。
∴PA⊥BE ∴BE⊥面 PAC，DE 面 PAC ∴BE⊥DE
a 3 a ，EC＝， 2 2 2 2 在△ PAC 中，DE＝ EC＝ a 2 4 3 a BE 在 Rt△DEB 中，tan∠BDE＝＝ 2 ＝ 6。 DE 2 a 4
在△ ABC 中，BE＝法三（射影面积法）：过 B 作 BD⊥AC 于 D，连接 PD，则△PDC 就是△PBC 在面 PAC 内的射影。
2. 线面垂直法：在二面角 α— l —β 的面 β 上取一点 P，作 AP⊥α 于 A， BP⊥ l 于 B，则∠ABP 即为 α— l —β 的平面角。

2018年高考试题分类汇编(立体几何)

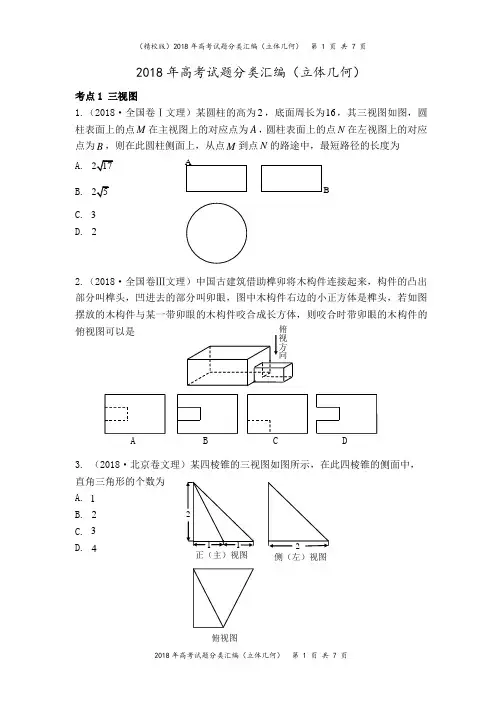
2018年高考试题分类汇编（立体几何）考点1 三视图1.（2018·全国卷Ⅰ文理）某圆柱的高为2，底面周长为16，其三视图如图，圆柱表面上的点M 在主视图上的对应点为A ，圆柱表面上的点N 在左视图上的对应点为B ，则在此圆柱侧面上，从点M 到点N 的路途中，最短路径的长度为A.B. C. 3 D. 22.（2018·全国卷Ⅲ文理）中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进去的部分叫卯眼，图中木构件右边的小正方体是榫头，若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是3. （2018·北京卷文理）某四棱锥的三视图如图所示，在此四棱锥的侧面中，直角三角形的个数为 A. 1 B. 2 C. 3 D. 4ABABCD正（主）视图侧（左）视图俯视图4.（2018·浙江卷）某几何体的三视图如图所示（单位：cm ），则该几何体的体积（单位：3cm ）是 A ．2 B ．4 C ．6 D ．8考点2 有关度量关系（选择题或填空题）考法1 角度1.（2018·全国卷Ⅱ文科）在正方体1111ABCD A B C D -中，E 为棱1CC 的中点，则异面直线AE 与CD 所成角的正切值为 A．2 B2. （2018·全国卷Ⅱ理科）在长方体1111ABCD A B C D -中，AB =1BC =，1AA =则异面直线1AD 与1DB 所成角的余弦值为A ．15B．6 C．5 D．23．（2018·浙江卷）已知四棱锥S ABCD -的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点），设SE 与BC 所成的角为1θ，SE 与平面ABCD 所成的角为2θ，二面角S AB C --的平面角为3θ，则A ．123θθθ≤≤B ．321θθθ≤≤ C. 132θθθ≤≤ D ．231θθθ≤≤ 考法2 面积1.（2018·全国卷Ⅰ理科）已知正方体的棱长为1，每条棱与平面α所成的角都相等，则α截此正方体所得的截面面积最大值为B.C.正视图侧视图2.（2018·全国卷Ⅰ文科）已知圆柱的上、下底面中心分别为1O ，2O ,过12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为A. B. 12π C.D. 10π3.（2018·全国卷Ⅱ理科）已知圆锥的顶点为S ,母线,SA SB 的所成角的余弦值为78，SA 与底面所成的角为45，若SAB ∆的面积为，则该圆锥的侧面积为．考法3 体积1.（2018·全国卷Ⅰ文科）在长方体1111ABCD A B C D -中，2AB BC ==，1AC 与平面11BB C C 所成的角为30，则长方体的体积为A.8B.C.D. 2.（2018·全国卷Ⅱ文科）已知圆锥的顶点为S ,母线,SA SB 互相垂直，SA 与底面所成的角为30，若SAB ∆的面积为8，则该圆锥的体积为．3.（2018·全国卷Ⅲ文理）设,,,A B C D 是同一个半径为4的球面上的四点，ABC ∆是等边三角形且其面积为，则三棱锥体积D ABC -的最大值为 A．B．C．D．4.（2018·天津卷文科）如图，已知正方体1111ABCD A B C D -的棱长为1，则四棱柱111A BB D D -5.（2018·天津卷理科）已知正方体1111ABCD A B C D -的棱长为1，除面ABCD 外，该正方体其余各面的中心分别为点,,,,E F G H M 如图)，则四棱锥M EFGH -的体CC 1积为 .6．（2018·江苏卷）如图所示，正方体的棱长为2，以其所有面的中心为顶点的多面体的体积为 .考点3 解答题1. （2018·全国卷Ⅰ理科）如图，四边形ABCD 为正方形，E ，F 分别为AD ，BC 的中点，以DF 为折痕把DFC ∆折起，使点C 到达P 的位置，且PF BF ⊥.（Ⅰ）证明：平面PEF ⊥平面ABFD ；（Ⅱ）若DP 与平面ABFD 所成的角的正弦值.2.（2018·全国卷Ⅰ文科）如图，在平行四边形ABCM 中，3AB AC ==,90ACM ∠=，以AC 为折痕将ACM ∆折起，使点M 到达点D 的位置，且AB DA ⊥.（Ⅰ）证明：平面ACD ⊥平面ABC ；（Ⅱ）Q 为线段AD 上的一点，P 为线段BC 上一点，且23BP DQ DA ==，求三棱锥QABP -的体积.PABC DEF ABCDA 1B 1C 1D 1MEF GH3.（2018·全国卷Ⅱ理科）如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====,O 为AC 的中点. （Ⅰ）证明：PO ⊥平面ABC ；（Ⅱ）若点M 在棱BC 上，且二面角M PA C --为30，求PC 与平面PAM 所成角的正弦值.4.（2018·全国卷Ⅱ文科）如图，在三棱锥P ABC -中，AB BC ==4PA PB PC AC ====,O 为AC 的中点. （Ⅰ）证明：PO ⊥平面ABC ；（Ⅱ）若点M 在棱BC 上，且2MC MB =，求点C 到平面POM 的距离.5. （2018·全国卷Ⅲ文理）如图，边长为2的正方形ABCD 所在的平面与半圆弧CD 所在的平面垂直，M 是CD 上异于,C D 的两点.（Ⅰ）证明：平面AMD ⊥平面BMC ；（Ⅱ）当三棱锥M ABC -体积最大时，求面MAB 与面MCD 所成得二面角的正弦ABCPMOABCPMOP ABCDQ M值.6.（2018·北京卷理科）如图，在三棱柱111ABC A B C -中，1CC ⊥平面ABC ，D ， E ，F ，G 分别为1AA ，AC ，11A C ，1BB的中点，AB BC ==12AC AA ==．（Ⅰ）求证：AC ⊥平面BEF ；（Ⅱ）求二面角1B CD C --的余弦值；（Ⅲ）证明：直线FG 与平面BCD 相交．7. （2018·北京卷文科）如图，在四棱锥P ABCD -中，底面ABCD 为矩形，平面PAD ⊥平面ABCD ，PA PD ⊥，PA PD =，,E F 分别为AD ，PB 的中点. （Ⅰ）求证：PE BC ⊥；（Ⅱ）求证：平面PAB ⊥平面PCD ；（Ⅲ）求证：EF ∥平面PCD .8.（2018·天津卷理科）如图，//AD BC 且2AD BC =，AD DC ⊥,//EG AD 且EG AD =，//CD FG 且2CD FG =，DG ⊥平面ABCD ，2DA DC DG ===. （Ⅰ）若M 为CF 的中点，N 为EG 的中点，求证：MN ∥平面CDE ；（Ⅱ）求二面角E BC F --的正弦值；（Ⅲ）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60，求线段DP 的长.ABCMDABCEDGA 1B 1C 1FABCDEFP9.（2018·天津卷文科）如图，在四面体ABCD 中，ABC ∆是等边三角形，平面 ABC ⊥平面ABD ，点M 为棱AB 的中点，2AB =，AD =90BAD ∠=．（Ⅰ）求证：AD BC ⊥；（Ⅱ）求异面直线BC 与MD 所成角的余弦值；（Ⅲ）求直线CD 与平面ABD 所成角的正弦值．10.（2018·江苏卷）在平行六面体1111ABCD A B C D -中，1AA AB =,111AB B C ⊥．求证：（Ⅰ）AB ∥平面11A B C ；（Ⅱ）平面11ABB A ⊥平面1A BC ．11.（2018·浙江卷）如图，已知多面体111ABC A B C -，1AA ，1BB ，1CC 均垂直于平面ABC ，ABC ∠120=,14AA =，11CC =，12AB BC BB ===．（Ⅰ）证明：1AB ⊥平面111A B C ；（Ⅱ）求直线1AC 与平面1ABB 所成的角的正弦值．A BCDEFGMNABCDMABCDA 1B 1C 1D 1ABCC 1A 1B 1。

2018高考数学立体几何含答案(最新整理)

5 ⎧⎪n ⋅ ⎨ 2018 高考数学立体几何答案1.（本小题 14 分）如图，在三棱柱 ABC − A 1B 1C 1 中， CC 1 ⊥ 平面 ABC ，D ，E ，F ，G 分别为 AA 1 ，AC ， A 1C 1 ， BB 1 的中点，AB=BC = ，AC = AA 1 =2．（Ⅰ）求证：AC ⊥平面 BEF ；（Ⅱ）求二面角 B−CD −C 1 的余弦值；（Ⅲ）证明：直线 FG 与平面 BCD 相交．【解析】（1）在三棱柱 ABC - A 1B 1C 1 中， Q CC 1 ⊥ 平面 ABC ，∴ 四边形 A 1 ACC 1 为矩形．又 E ， F 分别为 AC ， A 1C 1 的中点，∴ AC ⊥ EF ， Q AB = BC ，∴ AC ⊥ BE ，∴ AC ⊥ 平面 BEF ．（2）由（1）知 AC ⊥ EF ， AC ⊥ BE ，EF ∥CC 1 ．又CC 1 ⊥ 平面 ABC ，∴ EF ⊥ 平面 ABC ．Q BE ⊂ 平面 ABC ，∴ EF ⊥ BE ．如图建立空间直角坐称系 E - xyz ．由题意得 B (0, 2, 0) ， C (-1, 0, 0) ， D (1, 0,1) ， F (0, 0, 2) ， G (0, 2,1) ， ∴CD =(2, 0,1) ， CB =(1, 2, 0) ，设平面 BCD 的法向量为 n = (a , b , c ) ， u u u r CD = 0 ∴⎨ uur n ⋅ ，∴⎧2a + c = 0 ， a + 2b = 0 ⎩⎪ CB = 0 ⎩ 令 a = 2 ，则b = -1 ， c = -4 ，∴ 平面 BCD 的法向量 n = (2, - 1，, - 4) ，又Q 平面CDC 的法向量为EB=(0, 2, 0)，∴cos <n ⋅uur>=n ⋅EB= -21．1EB uurn EB 21由图可得二面角B -CD -C1为钝角，所以二面角B -CD -C1的余弦值为-21．21（3）平面BCD 的法向量为n =(2, - 1, - 4)，Q G (0, 2,1)，F (0, 0, 2)，∴GF =(0, - 2,1)，∴n ⋅GF =-2 ，∴n 与GF 不垂直，∴GF 与平面BCD 不平行且不在平面BCD 内，∴GF 与平面BCD 相交2．（本小题14 分）如图，在四棱锥P-ABCD中，底面ABCD 为矩形，平面PAD⊥平面ABCD ，PA ⊥PD ，PA =PD ， E ，F 分别为AD ，PB 的中点．（1）求证：PE ⊥BC ；（2）求证：平面PAB ⊥平面PCD ；（3）求证：EF∥平面PCD ．【解析】（1）Q PA =PD ，且E 为AD 的中点，∴PE ⊥AD ，Q 底面ABCD 为矩形，∴BC∥AD ，∴PE ⊥BC ．（2）Q 底面ABCD 为矩形，∴AB ⊥AD ，Q 平面PAD ⊥平面ABCD ，∴AB ⊥平面PAD ，∴AB ⊥PD ．又PA ⊥PD ，Q PD ⊥平面PAB ，∴平面PAB ⊥平面PCD ．（3）如图，取PC 中点G ，连接FG ，GD ．Q F ，G 分别为PB 和PC 的中点，∴FG∥BC ，且FG =1 BC ，2Q 四边形ABCD 为矩形，且E 为AD 的中点，∴ED∥BC ，DE =1 BC ，2∴ED∥FG ，且ED =FG ，∴四边形EFGD 为平行四边形，∴EF∥GD ，又EF ⊄平面PCD ，GD ⊂平面PCD ，∴EF∥ 平面PCD ．3 2 3 ⋅2 3 3．（12 分）如图，四边形 ABCD 为正方形， E , F 分别为 AD , BC 的中点，以 DF 为折痕把△DFC 折起，使点C 到达点 P 的位置，且 PF ⊥ BF .（1）证明：平面 PEF ⊥ 平面 ABFD ；（2）求 DP 与平面 ABFD 所成角的正弦值.解答：（1）E ,F 分别为 AD , BC 的中点，则 EF / / AB ，∴ EF ⊥ BF ，又 PF ⊥ BF ， EF ⋂ PF = F ，∴ BF ⊥ 平面 PEF ，BE ⊂ 平面 ABFD ，∴平面 PEF ⊥ 平面 ABFD .（2） PF ⊥ BF ， BF / / E D ，∴ PF ⊥ ED ，又 PF ⊥ PD ， ED ⋂ DP = D ，∴ PF ⊥ 平面 PED ，∴ PF ⊥ PE ，设 AB = 4 ，则 EF = 4 ， PF = 2 ，∴ PE = 2 ，过 P 作 PH ⊥ EF 交 EF 于 H 点，由平面 PEF ⊥ 平面 ABFD ，∴ PH ⊥ 平面 ABFD ，连结 DH ，则∠PDH 即为直线 DP 与平面 ABFD 所成的角，由 PE ⋅ PF = EF ⋅ PH ，∴ P H = = ， 4而 PD = 4 ，∴ sin ∠PDH =PH = 3 ，PD 4 ∴ DP 与平面 ABFD 所成角的正弦值 3. 4 4．（12 分）如图，在三棱锥 P - ABC 中， AB = BC = 2 AC 的中点．（1）证明： PO ⊥ 平面 ABC ；， PA = PB = PC = AC = 4 ， O 为（2）若点 M 在棱 BC 上，且二面角 M - PA - C 为30︒ ，求 PC 与平面 PAM 所成角的正弦值．2PO B M 3 3(a - 4)2 + 3a 2 + a 2 3 2 3 a - 42 3(a - 4)2 + 3a 2 + a 2u u u r ⎩AC【解析】（1）因为AP = CP = AC = 4 ， O 为 AC 的中点，所以OP ⊥ AC ，且OP = 2 ，连结OB ．因为 AB = BC =2 AC ，所以△ABC 为等腰直角三角形，2 且OB ⊥ AC ， OB = 1 AC = 2 ，由OP 2 + OB 2 = PB 2 知 PO ⊥ OB ， 2由OP ⊥ OB , OP ⊥ AC 知 PO ⊥ 平面 ABC ．（2）如图，以O 为坐标原点， OB 的方向为 x 轴正方向，建立空间直角坐标系O - xyz ．由已知得O (0, 0, 0) ， B (2, 0, 0) ， A (0, -2, 0) ， C (0, 2, 0) ， P (0, 0, 2 3 ) ， AP = (0, 2, 2 3 )，取平面 PAC 的法向量OB = (2, 0, 0) ，设 M (a , 2 - a , 0)(0 < a ≤ 2) ，则 AM = (a , 4 - a , 0) ，设平面 PAM 的法向量为 n = (x , y , z ) ．由 AP ⋅ n = 0 ， AM ⋅ n = 0 ， ⎧⎪2 y + 2 3z = 0 得⎨⎪a x + (4 - a ) y = 0 ，可取 n = ( 3 (a - 4), 3a , -a ) ，u u u r 2 3 (a - 4) u u u r ∴cos < OB , n >= ，由已知得 cos < OB , n > = ， 2 2∴ = 3 ，解得 a = -4 （舍去）， a = 4 ， ⎛ 8 3 4 3 4 ⎫ 2u u u r 3 u u u r 3 cos < ∴ n = - 3 , 3 , - 3 ⎪ ，又Q PC = (0, 2, -2 3 )，所以 PC , n >= ． 4 ⎝ ⎭ 3所以 PC 与平面 PAM 所成角的正弦值为 4． 5．（12 分）如图，边长为 2 的正方形 ABCD 所在的平面与半圆弧CD 所在平面垂直， M 是1 5 = - -2 5 CD 上异于C ， D 的点．（1）证明：平面 AMD ⊥ 平面 BMC ；（2）当三棱锥 M - ABC 体积最大时，求面 MAB 与面 MCD 所成二面角的正弦值．解答：（1）∵正方形 ABCD ⊥ 半圆面CMD ，∴ AD ⊥ 半圆面CMD ，∴ AD ⊥ 平面 MCD .∵ CM 在平面 MCD 内，∴ AD ⊥ CM ，又∵ M 是半圆弧CD 上异于C , D 的点，∴ CM ⊥ MD .又∵ AD I BCM ⊥ 平面 ADM .DM = D ，∴ CM ⊥ 平面 ADM ，∵ CM 在平面 BCM 内，∴平面（2）如图建立坐标系：∵ S ∆ABC 面积恒定，∴ MO ⊥ CD ，V M - ABC 最大.M (0, 0,1) ， A (2, -1, 0) ， B (2,1, 0) ， C (0,1, 0) ， D (0, -1, 0) ,设面 MAB 的法向量为 m = (x 1 , y 1 , z 1 ) ，设面 MCD 的法向量为 n = (x 2 , y 2 , z 2 ) ， MA (2, 1, 1) ， MB = (2,1, -1) ，MC = (0,1, -1) ， MD = (0, -1, -1) ，⎧2x 1 - y 1 - z 1 = 0 ⇒ ⎨2x + y - z = 0 m= (1, 0, 2) ， ⎩ 1 1 1同理 n = (1, 0, 0) ，∴c os = = 5 ，∴ sin = . 5 56.（本题满分 14 分，第 1 小题满分 6 分，第 2 小题满分 8 分）已知圆锥的顶点为 P ，底面圆心为 O ，半径为 2（1）设圆锥的母线长为4，求圆锥的体积；（2）设PO=4，OA，OB 是底面半径，且∠AOB=90°，M 为线段AB 的中点，如图，求异面直线PM 与OB 所成的角的大小.7.(本小题满分13 分)如图，AD∥BC 且AD=2BC，AD ⊥CD , EG∥AD 且EG=AD，CD∥FG 且CD=2FG，DG ⊥平面ABCD ，DA=DC=DG=2.（I）若M 为CF 的中点，N 为EG 的中点，求证：MN∥平面CDE ；（II）求二面角E -BC -F 的正弦值；（III）若点P 在线段DG 上，且直线BP 与平面ADGE 所成的角为60°，求线段DP 的长.【解析】依题意，可以建立以D 为原点，y z分别以DA ，DC ，DG 的方向为x 轴，轴，轴的正方向的空间直角坐标系（如图），可得D (0, 0, 0)，A(2, 0, 0)，B (1, 2, 0)， C (0, 2, 0)，m ⋅ n m n h 2 + 5h 2 + 52 0 ⋅ E (2, 0, 2) ， F (0,1, 2) ， G (0, 0, 2) ， M ⎛ 0,3 ,1⎫ ，N (1, 0, 2) ． 2 ⎪ ⎝ ⎭（1）依题意 DC = (0, 2, 0) ， DE = (2, 0, 2) ．⎧n ⋅ 设 n = ( x , y , z ) 为平面CDE 的法向量，则⎪ 0 DC = 0 ⎧ 即 2 y = 0 ， 0⎨n ⋅ = 0 ⎨2x + 2z = 0不妨令 z = –1 ，可得 n 0 = (1, 0, -1) ．⎩⎪ 0 DE ⎩ ⎛ 3 ⎫ 又 MN = 1,- ,1⎪ ，可得 MN ⋅ n = 0 ， ⎝ ⎭又因为直线 MN ⊄ 平面CDE ，所以 MN ∥平面CDE ．（2）依题意，可得 BC = (–1, 0, 0) ， BE = (1, -2, 2) ， CF = (0, -1, 2) ．⎧n ⋅ 设 n = ( x , y , z ) 为平面 BCE 的法向量，则⎪ BC = 0 ⎧ 即 -x = 0 ， ⎨n ⋅ = 0 ⎨x - 2 y + 2z = 0 不妨令 z = 1 ，可得 n = (0,1,1) ．⎩⎪ BE⎩ ⎧m ⋅ 设 m = ( x , y , z ) 为平面 BCF 的法向量，则⎪ BC = 0 ⎧ 即 -x = 0 ， ⎨m ⋅ = 0 ⎨- y + 2z = 0不妨令 z = 1 ，可得 m = (0, 2,1) ．⎩⎪ BF ⎩ 因此有cos < m , n >= = 3 10 ，于是sin < m , n >= 10所以，二面角 E – BC – F 的正弦值为 10 ．1010 ．10 （3）设线段 DP 的长为 h (h ∈[0, 2])，则点 P 的坐标为(0, 0, h ) ，可得= (-1, -2, h ) ．易知， = (0, 2, 0) 为平面 ADGE 的一个法向量， BP DC BP DC 2故 cos < BP ⋅ DC > = =， BP DC 由题意，可得 2 = sin 60︒ = 3 ，解得 h = 2 3 ∈[0, 2] ． 3 所以线段 DP 的长为 3 ．32 (2 3)2 +12 13 5 2 8．（本题满分 15 分）如图，已知多面体 ABCA 1B 1C 1，A 1A ，B 1B ，C 1C 均垂直于平面 ABC ，∠ ABC =120°，A 1A =4，C 1C =1，AB =BC =B 1B =2．（Ⅰ）证明：AB 1⊥平面 A 1B 1C 1；（Ⅱ）求直线 AC 1 与平面 ABB 1 所成的角的正弦值．解答：（1）∵ AB = B 1B = 2 ，且 B 1B ⊥ 平面 ABC ，∴ B 1B ⊥ AB ，∴ AB 1 = 2 .同理， AC 1 == =. 过点C 1 作 B 1B 的垂线段交 B 1B 于点G ，则C 1G = BC = 2 且 B 1G = 1，∴ B 1C 1 = . 在∆AB C 中， AB 2 + B C 2 = AC 2 ， 1 1 1 1 1 1∴ AB 1 ⊥ B 1C 1 ，①过点 B 1 作 A 1 A 的垂线段交 A 1 A 于点 H .则 B 1H = AB = 2 ， A 1H = 2 ，∴ A 1B 1 = 2 .在∆A B A 中， AA 2 = AB 2 + A B 2 ， 1 1 1 1 1 1∴ AB 1 ⊥ A 1B 1 ，②综合①②，∵ A 1B 1 ⋂ B 1C 1 = B 1 ， A 1B 1 ⊂ 平面 A 1B 1C 1 ， B 1C 1 ⊂ 平面 A 1B 1C 1 ， ∴ AB 1 ⊥ 平面 A 1B 1C 1 .（2）过点 B 作 AB 的垂线段交 AC 于点 I ，以 B 为原点，以 AB 所在直线为 x 轴，以 BI 所在直线为 y 轴，以 B 1B 所在直线为z轴，建立空间直角坐标系B - xyz .AC 2 + C C 2 13 1⨯ 13 39 ⎩ 则 B (0, 0, 0) ， A (-2, 0, 0) ， B 1 (0, 0, 2) ， C 1 (1, 3,1) ，设平面 ABB 的一个法向量 = (a , b , c ) ，1 n⎧⎪ 则 n ⋅ AB = 0 ⇒ ⎧2a = 0 ，令b = 1，则 n = (0,1, 0) ， ⎨⎪⎩n ⋅ BB 1 = 0 ⎨2c = 039又∵ AC 1 = (3, 3,1) ， cos < n , AC 1 >= = 13 .由图形可知，直线 AC 1 与平面 ABB 1 所成角为锐角，设 AC 1 与平面 ABB 1 夹角为. ∴ s in = . 139．（本小题满分 14 分）在平行六面体 ABCD - A 1B 1C 1D 1 中， AA 1 = AB , AB 1 ⊥B 1C 1 ．求证：（1） AB ∥平面A 1B 1C ；（2）平面ABB 1 A 1 ⊥ 平面A 1BC ．【解析】（1）在平行六面体 ABCD - A 1B 1C 1D 1 中， AB ∥A 1B 1．因为 AB ⊄ 平面 A 1B 1C ， A 1B 1 ⊂ 平面 A 1B 1C ，所以 AB ∥平面 A 1B 1C ．（2）在平行六面体 ABCD - A 1B 1C 1D 1 中，四边形 ABB 1 A 1 为平行四边形．又因为 AA 1 = AB ，所以四边形 ABB 1 A 1 为菱形，因此 AB 1 ⊥ A 1B ．又因为 AB 1 ⊥ B 1C 1 ， BC ∥B 1C 1 ，所以 AB 1 ⊥ BC ．又因为 A 1B BC = B ， A 1B ⊂ 平面 A 1BC ， BC ⊂ 平面 A 1BC ，所以AB1 ⊥平面A1BC ．因为AB1 ⊂平面ABB1 A1，所以平面ABB1 A1⊥平面A1BC ．“”“”At the end, Xiao Bian gives you a passage. Minand once said, "people who learn to learn are very happy people.". In every wonderful life, learning is an eternal theme. As a professional clerical and teaching position, I understand the importance of continuous learning, "life is diligent, nothing can be gained", only continuous learning can achieve better self. Only by constantly learning and mastering the latest relevant knowledge, can employees from all walks of life keep up with the pace of enterprise development and innovate to meet the needs of the market. This document is also edited by my studio professionals, there may be errors in the document, if there are errors, please correct, thank you!。

【大师特稿】2018届高考数学(理)热点题型：立体几何(含答案)

立体几何热点一空间点、线、面的位置关系及空间角的计算空间点、线、面的位置关系通常考查平行、垂直关系的证明，一般出现在解答题的第(1)问，解答题的第(2)问常考查求空间角，求空间角一般都可以建立空间直角坐标系，用空间向量的坐标运算求解.【例1】如图，在△ABC中，∠ABC＝π4，O为AB边上一点，且3OB＝3OC＝2AB，已知PO⊥平面ABC，2DA＝2AO＝PO，且DA∥PO.(1)求证：平面PBD⊥平面COD；(2)求直线PD与平面BDC所成角的正弦值.(1)证明∵OB＝OC，又∵∠ABC＝π4，∴∠OCB＝π4，∴∠BOC＝π2.∴CO⊥AB.又PO⊥平面ABC，OC⊂平面ABC，∴PO⊥OC.又∵PO，AB⊂平面PAB，PO∩AB＝O，∴CO⊥平面PAB，即CO⊥平面PDB.又CO⊂平面COD，∴平面PDB⊥平面COD.(2)解以OC，OB，OP所在射线分别为x，y，z轴，建立空间直角坐标系，如图所示.设OA ＝1，则PO ＝OB ＝OC ＝2，DA ＝1.则C(2，0，0)，B(0，2，0)，P(0，0，2)，D(0，－1，1)， ∴PD→＝(0，－1，－1)，BC →＝(2，－2，0)，BD →＝(0，－3，1). 设平面BDC 的一个法向量为n ＝(x ，y ，z )， ∴⎩⎪⎨⎪⎧n ·BC →＝0，n ·BD →＝0，∴⎩⎨⎧2x －2y ＝0，－3y ＋z ＝0，令y ＝1，则x ＝1，z ＝3，∴n ＝(1，1，3). 设PD 与平面BDC 所成的角为θ，则sin θ＝⎪⎪⎪⎪⎪⎪⎪⎪PD→·n |PD →||n | ＝⎪⎪⎪⎪⎪⎪1×0＋1×（－1）＋3×（－1）02＋（－1）2＋（－1）2×12＋12＋32＝22211. 即直线PD 与平面BDC 所成角的正弦值为22211. 【类题通法】利用向量求空间角的步骤第一步：建立空间直角坐标系. 第二步：确定点的坐标.第三步：求向量(直线的方向向量、平面的法向量)坐标. 第四步：计算向量的夹角(或函数值). 第五步：将向量夹角转化为所求的空间角.第六步：反思回顾.查看关键点、易错点和答题规范.【对点训练】如图所示，在多面体A 1B 1D 1DCBA 中，四边形AA 1B 1B ，ADD 1A 1，ABCD 均为正方形，E 为B 1D 1的中点，过A 1，D ，E 的平面交CD 1于F . (1)证明：EF ∥B 1C .(2)求二面角E -A 1D B 1的余弦值.(1)证明由正方形的性质可知A 1B 1∥AB ∥DC ，且A 1B 1＝AB ＝DC ，所以四边形A 1B 1CD 为平行四边形，从而B 1C ∥A 1D ，又A 1D ⊂面A 1DE ，B 1C ⊄面A 1DE ，于是B 1C ∥面A 1DE.又B 1C ⊂面B 1CD 1，面A 1DE ∩面B 1CD 1＝EF ，所以EF ∥B 1C.(2)解因为四边形AA 1B 1B ，ADD 1A 1，ABCD 均为正方形，所以AA 1⊥AB ，AA 1⊥AD ，AB ⊥AD 且AA 1＝AB ＝AD .以A 为原点，分别以AB →，AD →，AA 1→为x 轴，y轴和z 轴单位正向量建立如图所示的空间直角坐标系，可得点的坐标A (0，0，0)，B (1，0，0)，D (0，1，0)，A 1(0，0，1)，B 1(1，0，1)，D 1(0，1，1)，而E 点为B 1D 1的中点，所以E 点的坐标为⎝ ⎛⎭⎪⎫12，12，1.设平面A 1DE 的一个法向量n 1＝(r 1，s 1，t 1)，而该面上向量A 1E →＝⎝ ⎛⎭⎪⎫12，12，0，A 1D→＝(0，1，－1)，由n 1⊥A 1E →，n 1⊥A 1D →得r 1，s 1，t 1应满足的方程组⎩⎪⎨⎪⎧12r 1＋12s 1＝0，s 1－t 1＝0，(－1，1，1)为其一组解，所以可取n 1＝(－1，1，1).设平面A 1B 1CD 的一个法向量n 2＝(r 2，s 2，t 2)，而该面上向量A 1B 1→＝(1，0，0)，A 1D →＝(0，1，－1)，由此同理可得n 2＝(0，1，1). 所以结合图形知二面角E -A 1D B 1的余弦值为|n 1·n 2||n 1|·|n 2|＝23×2＝63.热点二立体几何中的探索性问题此类试题一般以解答题形式呈现，常涉及线、面平行、垂直位置关系的探究或空间角的计算问题，是高考命题的热点，一般有两种解决方式： (1)根据条件作出判断，再进一步论证；(2)利用空间向量，先假设存在点的坐标，再根据条件判断该点的坐标是否存在. 【例2】如图，在四棱锥P －ABCD 中，平面PAD ⊥平面ABCD ，PA ⊥PD ，PA ＝PD ，AB ⊥AD ，AB ＝1，AD ＝2，AC ＝CD ＝ 5. (1)求证：PD ⊥平面PAB ；(2)求直线PB 与平面PCD 所成角的正弦值；(3)在棱PA 上是否存在点M ，使得BM ∥平面PCD ？若存在，求AMAP 的值；若不存在，说明理由.(1)证明因为平面PAD ⊥平面ABCD ，平面PAD ∩平面ABCD ＝AD ，AB ⊥AD ，所以AB ⊥平面PAD ，所以AB ⊥PD.又PA ⊥PD ，AB ∩PA ＝A ，所以PD ⊥平面PAB. (2)解取AD 的中点O ，连接PO ，CO. 因为PA ＝PD ，所以PO ⊥AD.因为PO ⊂平面PAD ，平面PAD ⊥平面ABCD ，所以PO ⊥平面ABCD.因为CO ⊂平面ABCD ，所以PO ⊥CO. 因为AC ＝CD ，所以CO ⊥AD.如图，建立空间直角坐标系O －xyz.由题意得，A(0，1，0)，B(1，1，0)，C(2，0，0)，D(0，－1，0)，P(0，0，1).设平面PCD 的一个法向量为n ＝(x ，y ，z )，则 ⎩⎪⎨⎪⎧n ·PD →＝0，n ·PC →＝0，即⎩⎨⎧－y －z ＝0，2x －z ＝0，令z ＝2，则x ＝1，y ＝－2. 所以n ＝(1，－2，2).又PB →＝(1，1，－1)，所以cos 〈n ，PB →〉＝n ·PB →|n ||PB →|＝－33.所以直线PB 与平面PCD 所成角的正弦值为33.(3)解设M 是棱P A 上一点，则存在λ∈[0，1]，使得AM →＝λAP →.因此点M (0，1－λ，λ)，BM→＝(－1，－λ，λ).因为BM ⊄平面PCD ，所以要使BM ∥平面PCD ，则BM →·n ＝0，即(－1，－λ，λ)·(1，－2，2)＝0，解得λ＝14. 所以在棱P A 上存在点M ，使得BM ∥平面PCD ，此时AM AP ＝14.【类题通法】(1)对于存在判断型问题的求解，应先假设存在，把要成立的结论当作条件，据此列方程或方程组，把“是否存在”问题转化为“点的坐标是否有解，是否有规定范围内的解”等.(2)对于位置探究型问题，通常借助向量，引进参数，综合已知和结论列出等式，解出参数.【对点训练】如图，在四棱锥P －ABCD 中，PD ⊥平面ABCD ，AB ∥DC ，AB ⊥AD ，DC ＝6，AD ＝8，BC ＝10，∠P AD ＝45°，E 为P A 的中点.(1)求证：DE∥平面BPC；(2)线段AB上是否存在一点F，满足CF⊥DB？若存在，试求出二面角F－PC－D 的余弦值；若不存在，请说明理由.(1)证明取PB的中点M，连接EM和CM，过点C作CN⊥AB，垂足为点N.∵CN⊥AB，DA⊥AB，∴CN∥DA，又AB∥CD，∴四边形CDAN为平行四边形，∴CN＝AD＝8，DC＝AN＝6，在Rt△BNC中，BN＝BC2－CN2＝102－82＝6，∴AB＝12，而E，M分别为P A，PB的中点，∴EM∥AB且EM＝6，又DC∥AB，∴EM∥CD且EM＝CD，四边形CDEM为平行四边形，∴DE∥CM.∵CM⊂平面PBC，DE⊄平面PBC，∴DE∥平面BPC.(2)解由题意可得DA，DC，DP两两互相垂直，如图，以D为原点，DA，DC，DP分别为x，y，z轴建立空间直角坐标系D－xyz，则A (8，0，0)，B (8，12，0)，C (0，6，0)，P (0，0，8). 假设AB 上存在一点F 使CF ⊥BD ，设点F 坐标为(8，t ，0)，则CF→＝(8，t －6，0)，DB →＝(8，12，0)，由CF→·DB →＝0得t ＝23. 又平面DPC 的一个法向量为m ＝(1，0，0)，设平面FPC 的法向量为n ＝(x ，y ，z ). 又PC→＝(0，6，－8)，FC →＝⎝ ⎛⎭⎪⎫－8，163，0. 由⎩⎪⎨⎪⎧n ·PC →＝0，n ·FC →＝0，得⎩⎪⎨⎪⎧6y －8z ＝0，－8x ＋163y ＝0，即⎩⎪⎨⎪⎧z ＝34y ，x ＝23y ，不妨令y ＝12，有n ＝(8，12，9).则cos 〈n ，m 〉＝n ·m |n ||m |＝81×82＋122＋92＝817.又由图可知，该二面角为锐二面角，故二面角F －PC －D 的余弦值为817. 热点三立体几何中的折叠问题将平面图形沿其中一条或几条线段折起，使其成为空间图形，这类问题称为立体几何中的折叠问题，折叠问题常与空间中的平行、垂直以及空间角相结合命题，考查学生的空间想象力和分析问题的能力.【例3】如图，菱形ABCD 的对角线AC 与BD 交于点O ，AB ＝5，AC ＝6，点E ，F 分别在AD ，CD 上，AE ＝CF ＝54，EF 交BD 于点H .将△DEF 沿EF 折到△D ′EF 的位置，OD ′＝10. (1)证明：D ′H ⊥平面ABCD ； (2)求二面角B －D ′A －C 的正弦值.(1)证明由已知得AC ⊥BD ，AD ＝CD . 又由AE ＝CF 得AE AD ＝CFCD ，故AC ∥EF . 因此EF ⊥HD ，从而EF ⊥D ′H .由AB ＝5，AC ＝6得DO ＝BO ＝AB 2－AO 2＝4. 由EF ∥AC 得OH DO ＝AE AD ＝14.所以OH ＝1，D ′H ＝DH ＝3. 于是D ′H 2＋OH 2＝32＋12＝10＝D ′O 2，故D ′H ⊥OH . 又D ′H ⊥EF ，而OH ∩EF ＝H ，所以D ′H ⊥平面ABCD .(2)解如图，以H 为坐标原点，HF →的方向为x 轴正方向，建立空间直角坐标系H－xyz .则H (0，0，0)，A (－3，－1，0)， B (0，－5，0)，C (3，－1，0)，D ′(0，0，3)，AB →＝(3，－4，0)，AC →＝(6，0，0)，AD ′→＝(3，1，3). 设m ＝(x 1，y 1，z 1)是平面ABD ′的一个法向量，则⎩⎪⎨⎪⎧m ·AB →＝0，m ·AD ′→＝0，即⎩⎨⎧3x 1－4y 1＝0，3x 1＋y 1＋3z 1＝0，所以可取m ＝(4，3，－5).设n ＝(x 2，y 2，z 2)是平面ACD ′的一个法向量，则⎩⎪⎨⎪⎧n ·AC →＝0，n ·AD ′→＝0，即⎩⎨⎧6x 2＝0，3x 2＋y 2＋3z 2＝0，所以可取n ＝(0，－3，1).于是cos 〈m ，n 〉＝m ·n |m ||n |＝－1450×10＝－7525.sin 〈m ，n 〉＝29525.因此二面角B －D ′A －C 的正弦值是29525.【类题通法】立体几何中的折叠问题，关键是搞清翻折前后图形中线面位置关系和度量关系的变化情况，一般地翻折后还在同一个平面上的性质不发生变化，不在同一个平面上的性质发生变化.【对点训练】如图1，在直角梯形ABCD 中，AD ∥BC ，∠BAD ＝π2，AB ＝BC ＝1，AD ＝2，E 是AD 的中点，O 是AC 与BE 的交点.将△ABE 沿BE 折起到△A 1BE 的位置，如图2.(1)证明：CD ⊥平面A 1OC ；(2)若平面A 1BE ⊥平面BCDE ，求平面A 1BC 与平面A 1CD 夹角的余弦值.(1)证明在题图1中，因为AB ＝BC ＝1，AD ＝2，E 是AD 的中点，∠BAD ＝π2，所以BE ⊥AC .即在题图2中，BE ⊥OA 1，BE ⊥OC ，从而BE ⊥平面A 1OC .又CD ∥BE ，所以CD ⊥平面A 1OC . (2)解由已知，平面A 1BE ⊥平面BCDE ，又由(1)知，BE ⊥OA 1，BE ⊥OC ，所以∠A 1OC 为二面角A 1－BE －C 的平面角，所以∠A 1OC ＝π2.如图，以O 为原点，OB →，OC →，OA 1→分别为x 轴、y 轴、z 轴正方向建立空间直角坐标系，因为A 1B ＝A 1E ＝BC ＝ED ＝1，BC ∥ED ，所以B ⎝ ⎛⎭⎪⎫22，0，0，E ⎝ ⎛⎭⎪⎫－22，0，0，A 1⎝ ⎛⎭⎪⎫0，0，22，C ⎝ ⎛⎭⎪⎫0，22，0，得BC →＝⎝ ⎛⎭⎪⎫－22，22，0，A 1C →＝⎝ ⎛⎭⎪⎫0，22，－22，CD →＝BE →＝(－2，0，0). 设平面A 1BC 的一个法向量n 1＝(x 1，y 1，z 1)，平面A 1CD 的一个法向量n 2＝(x 2，y 2，z 2)，平面A 1BC 与平面A 1CD 的夹角为θ，则⎩⎪⎨⎪⎧n 1·BC →＝0，n 1·A 1C →＝0，得⎩⎨⎧－x 1＋y 1＝0，y 1－z 1＝0，取n 1＝(1，1，1)；⎩⎪⎨⎪⎧n 2·CD →＝0，n 2·A 1C →＝0，得⎩⎨⎧x 2＝0，y 2－z 2＝0，取n 2＝(0，1，1)，从而cos θ＝|cos 〈n 1，n 2〉|＝23×2＝63，即平面A 1BC 与平面A 1CD 夹角的余弦值为63.。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2018届高考数学立体几何（理科）专题02 二面角1．如图，在三棱柱111ABC A B C -中， 1,90A A AB ABC =∠=︒侧面11A ABB ⊥底面ABC .(1)求证： 1AB ⊥平面1A BC ；(2)若15360AC BC A AB ==∠=︒，，,求二面角11B A C C --的余弦值.且，,，，平面平面，点为的中点．（1）过点作一个平面与平面平行，并说明理由；（2）求平面与平面所成锐二面角的余弦值．3．如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形， 2AB AD =， BD =，且PD ⊥底面ABCD . （1）证明：平面PBD ⊥平面PBC ；（2）若Q 为PC 的中点，且1AP BQ ⋅=，求二面角Q BD C --的大小.4．如图所示的几何体是由棱台和棱锥拼接而成的组合体，其底面四边形是边长为2的菱形，，平面. （1）求证：；（2）求平面与平面所成锐角二面角的余弦值.5．在四棱锥P ABCD -中，四边形ABCD 是矩形，平面PAB ⊥平面ABCD ，点E 、F 分别为BC 、AP 中点.（1）求证： //EF 平面PCD ；（2）若0,120,AD AP PB APB ==∠=，求平面DEF 与平面PAB 所成锐二面角的余弦值.6．如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形, ,90AD BC ADC ∠=,平面PAD ⊥底面ABCD ,Q 为AD 中点, M 是棱PC 上的点, 12,1,2PA PD BC AD CD =====（Ⅰ）若点M 是棱PC 的中点,求证: PA 平面BMQ ; （Ⅱ）求证:平面PQB ⊥平面PAD ;（Ⅲ）若二面角M BQ C --为30,设PM tMC =,试确定t 的值.2018届高考数学立体几何（理科）专题02 二面角（教师版）1．如图，在三棱柱111ABC A B C -中， 1,90A A AB ABC =∠=︒侧面11A ABB ⊥底面ABC . (1)求证： 1AB ⊥平面1A BC ；(2)若15360AC BC A AB ==∠=︒，，,求二面角11B A C C --的余弦值.【答案】（1）证明见解析；（2）14-.侧面11A ABB ⊥底面,90ABC ABC ∠=︒，CB ∴⊥侧面11A ABB ，1CB AB ∴⊥. 又1A B BC B ⋂=,1AB ∴⊥平面1A BC .(2)在Rt ABC 中， 5,3,4AC BC AB ==∴=,又菱形11A ABB 中， 160A AB ∠=︒，1A AB ∴为正三角形.设(),,n x y z =为平面11A CC的方向量，则1110,20,{{0.230.n C C x n C A x z =-+=∴=+-=令3x =,得()n =为平面11A CC 的一个法向量.又()10,OB =-为平面1A BC 的一个法向量，111cos , 142723n OB n OB n OB===-.∴二面角11B A C C --的余弦值为. 2．如图所示的多面体中，下底面平行四边形与上底面平行，且，,，，平面平面，点为的中点．（1）过点作一个平面与平面平行，并说明理由；（2）求平面与平面所成锐二面角的余弦值．【答案】（1）见解析；（2）试题解析：（1）取的中点，的中点，连接、、，如图所示．则平面平面，平面即为所求的平面．理由如下：在平行四边形中，点分别是与的中点，所以，在中，点分别是的中点，所以．显然，，所以平面平面，亦即平面平面．（2）不妨设,,，故,．在平行四边形中，，所以．取的中点，则．又平面平面，平面平面，所以平面．连接，因为，，所以，又，所以．如图所示，以点为坐标原点建立空间直角坐标系，则，，，，，，,，．所以，，，．设平面的法向量为，则由，即，整理得．令，．所以．所以．3．如图，在四棱锥P ABCD -中，底面ABCD 为平行四边形， 2AB AD =， BD =，且PD ⊥底面ABCD . （1）证明：平面PBD ⊥平面PBC ；（2）若Q 为PC 的中点，且1AP BQ ⋅=，求二面角Q BD C --的大小.【答案】（1）见解析（2）4π试题解析：（1）证明：∵222AD BD AB +=，∴AD BD ⊥，∴//AD BC ，∴BC BD ⊥. 又∵PD ⊥底面ABCD ，∴PD BC ⊥.∵PD BD D ⋂=，∴BC ⊥平面PBD . 而BC ⊂平面PBC ，∴平面PBC ⊥平面PBD . （2）解：由（1）知， BC ⊥平面PBD ，∴2112t AP BQ +⋅==，∴1t =.故1122DQ ⎛⎫=- ⎪ ⎪⎝⎭，11,22BQ ⎛⎫=- ⎪ ⎪⎝⎭. 设平面QBD 的法向量为(),,n x y z =，则0{ 0n DQ n BQ ⋅=⋅=，即110222{11022x y z x y z -++=-+=，令1x =，得()1,0,1n =. 易知平面BDC 的一个法向量为()0,0,1m =，则cos ,2m n ==，∴二面角Q BD C --的大小为4π. 4．如图所示的几何体是由棱台和棱锥拼接而成的组合体，其底面四边形是边长为2的菱形，，平面.（1）求证：；（2）求平面与平面所成锐角二面角的余弦值.【答案】（1）证明见解析；（2）.又棱台中，∴(2)建立空间直角坐标系如图所示，则，，，，，，所以，，，，设平面的一个法向量为，则,∴，.令，得， ∴；设平面的法向量为，则,∴，令，得，， ∴，设平面与平面所成锐二面角为，则，所以平面与平面所成锐二面角的余弦值为.5．在四棱锥P ABCD -中，四边形ABCD 是矩形，平面PAB ⊥平面ABCD ，点E 、F 分别为BC 、AP 中点.（1）求证： //EF 平面PCD ；（2）若0,120,AD AP PB APB ==∠=，求平面DEF 与平面PAB 所成锐二面角的余弦值.【答案】（1）见解析（2试题解析：（I ）证明：取PD 中点G ，连接,GF GC ．在△PAD 中，有 ,G F 分别为PD 、AP 中点∴ 1//2GF AD而GC ⊂平面PCD ， EF ⊄平面PCD ∴ //EF 平面PCD （II ）取AB 中点O ，连接OP ，设=2AD .四边形ABCD 是矩形∴ AD AB ⊥平面PAB ⊥平面ABCD ,平面PAB ⋂平面ABCD = AB ， AD ⊂平面PAB∴ AD ⊥平面PAB 又 AD AP PB ==， 0=120APB ∠， O 为AB 中点∴ OP AB ⊥，OA OB == 1OP =.故可建立空间直角坐标系O xyz -，如图所示，则0A ，）， 010P （，，），0B （，），()C ，)2D ∴1,02F ⎫⎪⎪⎝⎭，()E ∴()1DE =--，1,222DF ⎛⎫=-- ⎪ ⎪⎝⎭ 设(),,n x y z =是平面DEF 的一个法向量，则·0{ ·0DE n DF n ==，即0{ 1202z x y z --=+-=不妨设1x =，则(1,73,23n =--．易知向量()0,0,2AD =为平面PAB 的一个法向量．∴2·cos ,·1n ADn AD n AD ===故平面DEF 与平面PAB 6．如图,在四棱锥P ABCD -中,底面ABCD 为直角梯形, ,90AD BC ADC ∠=,平面PAD ⊥底面ABCD , Q 为AD 中点, M 是棱PC 上的点, 12,1,2PA PD BC AD CD =====（Ⅰ）若点M 是棱PC的中点,求证: PA 平面BMQ ;（Ⅱ）求证:平面PQB ⊥平面PAD ; （Ⅲ）若二面角M BQ C --为30,设PM tMC =,试确定t 的值.试题解析：因为MN ⊂平面BMQ , PA ⊄平面BMQ 所以PA 平面BMQ . （Ⅱ）因为1,,2AD BC BC AD Q =为AD 中点, 所以四边形BCDQ 为平行四边形,所以CD BQ .因为90ADC ∠=,所以90AQB ∠=,即AD BQ ⊥.又因为平面PAD ⊥平面ABCD ,且平面PAD ⋂平面ABCD AD =,所以BQ ⊥平面PAD ,因为BQ ⊂平面PQB ,所以平面PAD ⊥平面PQB .（Ⅲ）因为,PA PD Q =为AD 的中点,所以PQ AD ⊥.又因为平面PAD ⊥平面ABCD ,且平面PAD ⋂平面ABCD AD =,所以PQ ⊥平面ABCD以Q 为原点,以,QA QB 的方向分别为x 轴, y 轴的正方向,建立如图所示的空间直角坐标系Q xyz -, 则点()0,0,0Q , ()0,0,3P, ()B, ()C -,平面BQC 的一个法向量()0,0,1n =. 设(),,M x y z ,则(,,,PM x y z =,()1,MC x y z =---,因为PM tMC =所以())()11{ { t x t x t x y t y y z t z z =-+=--=⇒-=在平面MBQ 中, ()0,3,0,1t QB QM t ⎛==- +⎝⎭,因为二面角M BQ C --为30,所以cos303m n m n t ⋅==⋅+,所以3t =.。