测试信号分析与处理案例
信号分析与处理实验报告

实验一1、基本信号的表示及可视化(1)单位冲激信号 (t)程序:t=-1:0.001:1; %定义时间向量for i=1:3; %采用循环语句观察i取不同值时的图形dt=1/(i^4);X=(1/dt)*((t>=(-1/2*dt))-(t>=(1/2*dt)));%计算函数值subplot(1,3,i);%将图像分成三部分同时观察stairs(t,X);title('单位冲激信号δ(t)');end(2)单位阶跃信号程序:t=-0.5:0.001:1;%定义时间变量,间隔为0.001S=stepfun(t,0);%定义单位阶跃信号S1=stepfun(t,0.5);%定义单位阶跃延迟信号figure(1);plot(t,S);axis([-0.5 1 -0.2 1.2]);title('单位阶跃信号')%画出图形figure(2);plot(t,S1);axis([-0.5 1 -0.2 1.2]);title('单位阶跃延迟信号')(3)抽样信号f=sin(t)./t;程序:t=-10:0.6:10; %向量t时间范围t=t1:p:t2,p为时间间隔f=sin(t)./t;plot(t,f,'o'); %显示该信号的时域波形title('f(t)=Sa(t)(时间间隔为0.6s)'); %标题xlabel('t') %横坐标标题axis([-10,10,-0.4,1.1]) %横坐标和纵坐标范围(4)单位样值序列和单位阶跃序列A.单位序列δ(k)B.单位阶跃序列ε(k)程序:n1=-10;n2=10;%输入序列的起始点n=n1:n2;k=length(n);x1=zeros(1,k);x1(1,-n1+1)=1;%产生单位样值序列subplot(2,1,1);%绘图stem(n,x1,'filled');x2=ones(1,k);x2(1,1:-n1)=0;subplot(2,1,2);stem(n,x2,'filled');2、信号的频域分析已知周期方波信号0||2()0||22E t f t T t ττ⎧<⎪⎪=⎨⎪<<⎪⎩,当02T τ=, 04T τ=,08T τ=时,画出其幅度谱和相位谱,观察不同周期下,()f t 的频谱图有何区别。
测试信号分析与处理案例
101测试信号分析与处理案例【案例4。
1】在采用非抑制调幅技术设计测试系统时,如果调制波信号幅值有正有负,在调制前把调制波和一个足够大直流偏置信号相加。
解调后的信号再与同样的直流偏置信号相减。
否则解调波中的部分波形相位将发生180°滞后.【案例4.2】数字式电能表检测电能的工作原理大多是通过实时检测入户电压和电流,并将电压信号和电流信号进行乘法运算得到各时刻的瞬时电功率,并按时间积分电功率后得到电能值.【案例4。
3】在汽车进行平稳性试验时,测得汽车在某处的加速度的时域波形如图4。
7(a )所示。
将此信号送入信号处理机处理,获得图4。
7(b )所示的相关函数.由相关图看出车身振动含有某一周期振动信号,从两个峰值的时间间隔为s 11.0,可算出周期振动信号的频率为()Hz T f 911.011===(a )汽车加速度的时域波形 (b )汽车加速度的自相关函数图4。
7 加速度时域波形及其自相关函数【案例4.4】在一般正常情况下,悬臂梁的振动波形为正弦波,然而由于背景噪声或瞬间干扰等因素的影响,在一些时域区间信号的周期性难以呈现,为此利用自相关分析来识别采集信号的周期性,以判断测得信号是否含有较大的干扰信号.如图4。
8(引自参考文献20)所示,其中(a )为采集到的波形。
对原采集的振动波形进行自相关处理,得到的波形如图4.8(b )所示,自相关函数在时移1ms 时趋于零,毫无疑问悬臂梁振动波形无周期性,证明测得信号具有较大干扰信号。
【案例4。
5】在对某齿轮箱进行故障检测与诊断时,由于测取的振动信号信噪比很低,特征信号频率较高,信号消噪难度大,故障特征信号难以提取。
图4.9(引自参考文献21)为振动信号及其功率谱。
对原振动信号进行自相关计算,能有效消噪,提高信噪比。
图4。
10(引自参考文献21)为振动信号的自相关时域波形及其功率谱图。
可见信号经自相关计算后,时域图呈明显周期性,功率谱图中80Hz 频率十分明显.经分析,该频率信号是模拟不平衡、未校准、机械松动引起的低频干扰。
第二章 测试信号的分析与处理(3)

(4)两周期信号的互相关函数仍然是同频率的周期信号, 且保留原了信号的相位信息。
(5)两个非同频率的周期信号互不相关。
(6)随机噪声信号的自相关函数将随 的增大快速衰 减。
12
4 相关分析的工程应用
案例:机械加工表面粗糙度自相关分析
被测工件
相关分析
性质3,性质6:提取出回转误差等周期性的故障源。
13
案例:地下输油管道漏损位置的探测
X1 t
X2
14
5 功率谱分析及其应用(补充)
(1) 功率谱密度函数的定义 随机信号的自功率谱密度函数(自谱)是该随机信号自 相关函数的傅立叶变换,记为Sx(f):
其逆变换为:
15
(2) 功率谱密度函数的物理意义
Sx(f)随机信号的频域描述函数。
当τ =0时,有:
17
(3)功率谱在设备诊断中的应用
上图是汽车变速箱上加速度信号的功率谱图。图(a)是变速箱正
常工作谱图,(b)为机器运行不正常时的谱图。可以看到图(b)比
(a)增加了9.2Hz和18.4Hz两个谱峰,这两个频率就为设备故障
的诊断提供了依据。
18
19
11
3 相关函数的性质
相关函数描述了两个信号间或信号自身不同时刻的相似 程度,通过相关分析可以发现信号中许多有规律的东西。
(1)自相关函数是 的偶函数,RX()=Rx(- ); (2)当 =0 时,自相关函数具有最大值。
(3)周期信号的自相关函数仍然是同频率的周期 但不保留原信号的相位信息。
信号,
从而:
上式表明:Sx(f)曲线下的总面积与x2(t)/T曲线下的总面积相等。 从物理意义上讲,x2(t)是信号x(t)的能量,x2(t)/T是信号x(t)的
GSM路测分析案例(共67张)

案例 4 (àn lì)
硬件问题导致的切换失败
第11页,共67页。
第12页,共67页。
现象:路测时发现移动台向建设乡2,3小区发生连续的切换失败,
同时话务统计也反映建设乡三个扇区的出入切换成功率都很低。
解决:由于建设乡三个小区的出入切换成功率都很低,因 此我们排除了干扰的原因,怀疑是建设乡的硬件存在 (cúnzài)问题。后察看告警发现建设乡的TMU一直无法锁定
随后电平也迅速降低,下行链路误码增高未能及时切换导致掉 话。通过对数据的进一步分析,可能是由于主服务小区硬件问
题,建议检查TCH=8的载波板。
第3页,共67页。
案例 2 (àn lì)
无覆盖掉话
第4页,共67页。
第5页,共67页。
掉话发生在虎峰到大庙路段,从回放数据中可以看出, 将近0.5公里的路段覆盖很差,主服务小区BCCH=45,BSIC = 61,LAC=33165,CI=20009, TA=15,RxQual =7,RxLev=105dBm电平(diàn pínɡ)一直在-100dbm左右。由于没有信号好 时(cǐ shí)的服务小区为职高1(BCCH=106)
解决:从路测数据上看此时的话音质量较差,误码率较高,怀疑存 在干扰。通过其邻区列表我们发现一个与服务小区邻频的信号,
经查为电务段2(BCCH=105)的信号,其C/A>-6,因此断定属 于BCCH上的邻频干扰。于是修改职高1的BCCH频点,经过
我们判断16901和16902天线接反。导致移动台无法搜索到 可供切换的邻小区,从而导致无线链路超时而掉话。
第36页,共67页。
案例 11 (àn lì)
Tch分配失败导致的未接通
第37页,共67页。
信号分析与处理实验

n ωj �
e� n� h � � �
0�n 1� N
ωj
e� H
波滤想理的望希所近逼来 � n� h 列序应响样抽位单长限有用是理原本基的法计设数函窗
� n� ω 数函窗用以所 �的果因非是且 �列序长限无是往往 � n� d h 于由 。 � n� d h 应响样抽位单的器
�应响样抽位单的器波滤字数 RIF 的计设际实到得�理处权加行进并�断截 � n� d h 将
�s
式公
换变在以所�量变参的要紧关无个一了成就 T 期周样采�后标指域字数出给为因 。响影有没果结计设对 s T 变改�答 �么什为�响影无有果结计设对值取的 s T 的中
1� 1�
z � 1 sT z �1 2
�s
式公换变�中程过器波滤字数计设法换变性线双用
题考思�六�
。滑平更形波使�号信用有留保�号信扰干除滤是用作的器波滤�答
5x 4x的 �� x n x� 4 x为 �4 �的 ��7n 为 期 8n是 周 n�� � �因 x 结的确正是 61=N �期 � n� � 7果 x1 � � � n� 7 x 使果结�61 是期周的 � n� 5 x � � n� 56 �n �周
� n� 5 xj � � n� 4 x � � n� 8x .8
s
�
减衰小最带阻� p � 减衰大最带通� s � 率频止截限下带阻� p � 率频止截带通�有数参 。器波滤计设来换变性线双用采能才 �时偿补被能或的许容是真失性线非种这当有只 �答 �性特和数参的器波滤录记�四�
� 2 �1 � N � �
k � 1�
� z � neve H
N � k � 1�
性称对足满须必还 � n� h 则�位相性线求要果如
测试信号分析处理实验报告

《测试信号分析与处理》课程试验报告试验名称:快速傅立叶变换算法(FFT)在信号频谱分析中的应用及滤波器的设计和实现试验目的:通过本试验,基本掌握FFT算法的实现原理,同时能利用MATLAB语言编写完成FFT算法,并对给定的信号进行频谱分析。
按照给定的数字滤波器设计指标,完成相应数字滤波器的设计。
试验设备:通用计算机+MATLAB 6.0软件。
试验步骤:1、产生给定的需要分析的周期性信号,利用FFT算法对产生的周期性信号进行频谱分析。
2、按照给定的数字滤波器设计指标,设计完成相应的数字滤波器。
试验内容:1、理解FFT算法的基本原理;2、掌握MATLAB编程的基本语言;3、会利用MATLAB语言实现FFT算法。
4、利用实现的FFT算法对给定的周期性离散信号进行频谱分析,并绘出频谱图。
5、理解数字滤波器设计指标,完成数字滤波器设计。
试验的难点和要点:1、依据采样定理,对给定的信号选择合适的采样周期进行离散化。
2、熟练使用MATLAB语言中的FFT库函数对采样信号进行傅立叶变换。
3、利用MATLAB 绘图语言绘制傅立叶变换后的信号频谱图。
4、利用MATLAB 语言设计完成给定指标的数字滤波器。
试验过程记录:1、利用FFT 实现对信号频谱分析的基本原理(介绍试验内容中所涉及到的信号分析理论,注意介绍说明要规范和完整)本实验是求函数x=sin(2*pi*50*t)+sin(2*pi*25*t)的频谱曲线,实验中通过在0到1.023之间以0.001的间隔取了1024个点绘制两个正弦函数的叠加曲线,然后进行频谱分析。
由于序列的长度为1024=2^10,所以可以采用基2时析型FFT 算法。
序列长度1024=2^10,因此运算级数为10级。
第一步:先通过构造一个循环函数求出输入序列的按倒序重排的序列,然后接下来的运算是建立在这个重排序列的基础上。
第二步:通过构造一个三级嵌套循环求出该序列的傅里叶变换函数。
其中第三级循环函数中包含两个循环函数,第一个循环函数用来求出奇序列的值,第二个循环函数用来求出偶序列的值。
测试信号分析与处理-第3章(打印版)

关于 m = 0 偶对称。
即: m=-(N-1), …,-1,0,1,…,(N-1), 长度为2N-1
-4-
§3.1 相关函数估计的计算式
估计质量如何?
ˆ 估计均值: E[ Rxx (m)] = E[
N −|m|−1 1 ∑ x(n) x(n + m)] N − | m | n =0
§3.1 相关函数估计的计算式
j =1 n
⎡ sq(1) sq(1) sq(2) sq(1) ⎢ sq(1) sq(2) sq(2) sq(2) ⎢ 按从小到大排序, ⎢ M M 比较平方和: ⎢ ⎣ sq(1) sq(10) sq(2) sq(10)
sq(10) sq(1) ⎤ sq(10) sq(2) ⎥ ⎥ ⎥ O M ⎥ L sq(10) sq(10) ⎦ L L
相关函数和线性卷积运算的关系
x 线性卷积: (m) ∗ y (m) = ∑ x(m − k ) y (k )
N −1
相关函数和线性卷积运算的关系
说明: ● 相关函数与线性卷积的计算形式相似,都包 含着变量的移位、相乘和求和,差别只是卷 积多一个序列的翻转,因而两者仅差一个负 号;
●
相关函数:Rxy (m) =
l
x ( n) :
R 将平方和相近的波形相加求平均: _ model = ∑ R(i,:) (l − k + 1)
i=k
Rxy (m) :
- 27 -
- 28 -
相关运算
2. 自相关法检测信号的周期
信号的检测: x (n ) = s(n ) + u(n )
(白噪声)
y ( n) :
x (n ) 中有无 s (n) ?
第二章测试信号分析与处理(中)相关性分析

1 T
ò0T
x(t )
y(t
+t
)dt
分 析
=
lim
T ®¥
1 T
ò0T
x(t
-t
)
y(t)dt
及
= Ryx (-t )
应 用
互相关函数非奇非偶
测试 技术
相 对x(t) = X 0 sin(w1t + q1)和y(t) = Y0 sin(w2t + q2 )求Rxy (t )
关
分 析
Rxy
(t
)
=
1 T
分 器
用
测试 技术
3自相关分析
相
如y(t)=x(t), 可得自相关系数rx (t ) ,并有:
关 分 析
lim 1
ò T ®¥ T
T
0 [( x(t )-mx )( x(t +t )-mx )]dt
r (t ) = x
s
2 x
及 应 用
lim 1
ò T ®¥ T
T 0
x
(t
)
x
(t
+t
)
dt
-
mx2
析
及 应
Sy ( jf ) = H ( jf ) 2 Sx ( jf )
用
自谱分析可得系统幅频特性,缺相频特性
测试 技术
2、互谱
功 率
定义
谱
分 析
ò Sxy ( jf ) =
¥ -¥
Rxy
(t
)e
-
j
2p
f
t
dt
及 应 用
ò Rxy (t ) =
¥ -¥
S xy
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
测试信号分析与处理案例【案例4.1】在采用非抑制调幅技术设计测试系统时,如果调制波信号幅值有正有负,在调制前把调制波和一个足够大直流偏置信号相加。
解调后的信号再与同样的直流偏置信号相减。
否则解调波中的部分波形相位将发生180°滞后。
【案例4.2】数字式电能表检测电能的工作原理大多是通过实时检测入户电压和电流,并将电压信号和电流信号进行乘法运算得到各时刻的瞬时电功率,并按时间积分电功率后得到电能值。
【案例4.3】在汽车进行平稳性试验时,测得汽车在某处的加速度的时域波形如图4.7(a )所示。
将此信号送入信号处理机处理,获得图4.7(b )所示的相关函数。
由相关图看出车身振动含有某一周期振动信号,从两个峰值的时间间隔为s 11.0,可算出周期振动信号的频率为()Hz T f 911.011===(a )汽车加速度的时域波形 (b )汽车加速度的自相关函数图4.7 加速度时域波形及其自相关函数【案例4.4】在一般正常情况下,悬臂梁的振动波形为正弦波,然而由于背景噪声或瞬间干扰等因素的影响,在一些时域区间信号的周期性难以呈现,为此利用自相关分析来识别采集信号的周期性,以判断测得信号是否含有较大的干扰信号。
如图4.8(引自参考文献20)所示,其中(a )为采集到的波形。
对原采集的振动波形进行自相关处理,得到的波形如图4.8(b )所示,自相关函数在时移1ms 时趋于零,毫无疑问悬臂梁振动波形无周期性,证明测得信号具有较大干扰信号。
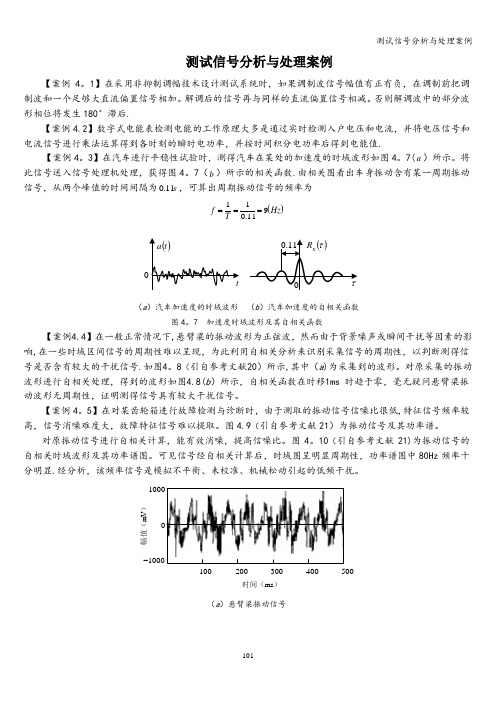
【案例4.5】在对某齿轮箱进行故障检测与诊断时,由于测取的振动信号信噪比很低,特征信号频率较高,信号消噪难度大,故障特征信号难以提取。
图4.9(引自参考文献21)为振动信号及其功率谱。
对原振动信号进行自相关计算,能有效消噪,提高信噪比。
图4.10(引自参考文献21)为振动信号的自相关时域波形及其功率谱图。
可见信号经自相关计算后,时域图呈明显周期性,功率谱图中80Hz 频率十分明显。
经分析,该频率信号是模拟不平衡、未校准、机械松动引起的低频干扰。
10020030040050010001000-时间(ms )幅值(m V )(a )悬臂梁振动信号.1-5.0-05.00.10300300-时间(ms )幅值(m V )(b )振动信号的自相关函数波形图4.8 悬臂梁振动信号分析)s (t )s m (2-⋅a(a )齿轮箱振动信号的时域波形)kHz (f )s m (2-⋅a(b )齿轮箱振动信号的功率谱图4.9 齿轮箱振动信号的时域波形及其功率谱)s m (2-⋅a )s (t(a )齿轮箱振动信号的自相关函数的时域波形图)kHz (f )s m (2-⋅a(b )齿轮箱振动信号的自相关函数的功率谱图4.10 齿轮箱振动信号的自相关函数的时域波形及其功率谱【案例4.6】测量运动速度。
互相关函数可用来测定汽车、炮弹、轧制钢带的速度,以及导管内和风洞内气流的速度等。
例如要测定炮弹的速度、可在相距l 米的两处设置两个光电式传感器如图4.12,炮弹通过时拾取反射光的信号做出互相关函数图,根据峰值出现的时间0τ如图4.12,即可求得速度τlv =v(a )炮弹飞行速度检测系统示意图 (b )互相关函数图4.12 炮弹飞行速度的测量【案例4.7】确定深埋在地下的输油管裂损的位置。
如图4.13所示,漏损处K 视为传播声源,两侧管道分别放置传感器,因为放传感器的两点距漏损处的距离不相等,放漏油的音响传至两传感器就有时差。
在互相关图上0ττ=处()τxy R 有最大值,这个0τ就是时差。
根据0τ便可确定漏损处的位置。
021τv S =式中:S ——两传感器的中点至漏油处的距离;v ——音响通过管道的传播速度。
(a )输油管破损位置检测系统示意图 (b )互相关函数图4.13 输油管裂损位置的检测【案例4.8】传递通道的确定。
利用互相关函数分析法可以检查引起汽车司机座振动的振源。
测试时在发动机、司机座和后轮轴上布置加速度计,并分别计算发动机和后轮轴上测得的信号与司机座测得信号的互相关函数,根据处理结果,发现发动机与司机座之间的相关性较差,而司机座与后轮之间的互相关函数出现明显的相关。
因此可以认为,司机座的振动主要是由于后轮的振动引起的。
【案例4.9】检测混淆在噪声中的信号。
由转子动不平衡引起的振动,是和转子同频率的周期信号,设其为()()x t x t x ϕω+=00sin 。
但用传感器测量该信号时,拾取的信号不可能是单纯的()t x ,而是混有各种随机干扰噪声,例如噪声()()∑=+=nn n n t n A t n 1sin ϕω。
为了提取出感兴趣的信号()t x ,可以利用自相关处理的办法,但自相关函数中只能反映信号()t x 的幅值(对应于动不平衡量的大小),而失去了相位信息(对应于动不平衡的方位)。
如果我们设法建立一个无噪声参考信号()()y t y t y ϕω+=00sin ,并用它去和拾取到的信号()()[]t n t x +作互相关处理,则由于()t n 与()t y 的频率无关,因而两者的互相关函数恒为零,只有()t x 与()t y 的互相关函数()τxy R 存在。
()τxy R 的幅值反应了动不平衡量的大小,峰值的偏移量0τ反映了相位差()x y ϕϕ-,若参考信号()t y 的y ϕ已知,就测出了不平衡的方位。
【案例4.10】 在MATLAB 中用多个谐波合成近似的周期方波。
在MA TLAB 命令界面下(Command Windows Font )键入如下程序: A=4; w0=pi/0.1; t=-0.5:.001:0.5;cosine=sin(w0*t)+(1/3)*sin(3*w0*t)+(1/5)*sin(5*w0*t)+(1/7)*sin(7*w0*t)+(1/9)*sin(9*w0*t)+(1/11)*sin(11*w0*t)+(1/13)*sin(13*w0*t)+(1/15)*sin(15*w0*t)+(1/17)*sin(17*w0*t)+(1/19)*sin(19*w0*t); plot(t,cosine)则可显示出图4.18所示的周期方波。
-0.5-0.4-0.3-0.2-0.100.10.20.30.40.5-1-0.8-0.6-0.4-0.200.20.40.60.81x (t )t图4.18 用谐波合成周期方波例4.2求图4.20所示的周期性三角波的幅频谱。
t2T 02T -()t x A图4.20 周期三角波解:()t x 在一个周期中可表达为()⎪⎪⎩⎪⎪⎨⎧+-=t T A A t T A A t x 22 0220<≤-≤≤t T T t因()()t x t x =-,故()t x 是偶函数,0=n b 。
222200A dt t T A A T a T=⎪⎭⎫ ⎝⎛-=⎰⎰⎪⎭⎫ ⎝⎛-=200cos 24T n tdt n t T A A T a ω2sin 4222ππn n A =⎪⎩⎪⎨⎧=0422πn A,6,4,2,5,3,1==n n其幅频谱(单边频谱)如图4.21(a )所示。
若用复数形式表示,则根据n n n a C C 21==- 00a C =可求得如图4.21(b )所示的幅频谱(双边频谱)。
2A na003ω05ω07ω0-03-05-07ω-0(a )单边频谱 (b )双边频谱图4.21 周期三角波幅频谱的两种形式【案例4.11】利用MA TLAB 绘出6/40()6/40sin(4ππππ++t t 的波形。
在MA TLAB 中编辑如下程序: A=4;w0=40*pi; phi=pi/6;t=-0.5:.001:0.5;cosine=A*sin(w0*t+phi)./(w0*t+phi); plot(t,cosine)则可显示出图4.25所示波形。
图4.25 在MA TLAB 中生成的sinc 函数【案例4.12】很多旋转机械故障(如点蚀、裂纹等)都表现为其振动信号中有异常冲激信号,因此采用固有频率很高的传感器检测,若机械有相关故障则传感器产生共振,而无故障机械则不会产生共振,则很容易可以检测机械相关故障。
【案例4.13】在幅度调制技术中,常应用乘法器将调制信号与高频正弦波(载波)相乘产生已调波。
高频正弦波的频谱函数为冲激函数。
设图4.27中()f U 为某调制信号的频谱,()()()s s f f f f f ++-=∆δδ为高频载波的频谱,根据傅里叶变换的频域卷积特性,已调波的频谱函数为调制信号频谱函数与高频载波频谱函数的卷积:()()()()()()00f f f U f f f U f U f -*++*=*∆δδ由式(4.31)()()()()s s f f U f f U f U f ++-=*∆fffsf sss图4.27 函数与δ函数的卷积【案例4.14】旋转机械不对中故障特性提取及诊断(引自参考文献22)对旋转机械转子系统不对中故障的机理进行理论分析,得出在不对中条件下旋转机械产生二倍频振动。
为验证这一结论,在转子实验台上对该类故障进行转子系统实验测试,并对测试信号进行频谱分析。
转子试验台及测量系统简图如图 4.30所示,将联轴器分开1mm 间隙,并将3号轴承垫高0.5mm ,用以模拟不对中故障,当转速达到3000r/min 时进行数据采集,然后对实验数据进行频谱和功率谱分析,其中一组结果如图4.31所示。
由于不对中位移及偏角的存在,使转子在高速运转时就会有一个两倍频的附加径向力作用于轴承上,从而激励转子产生振动频率为工频二倍的径向振动。
图4.30 实验装置及测试系统1-轴承1;2-轴承2;3-轴承3;4-轴承4;5-电动机; 6-皮带传动装置;7-轮盘;8-联轴器;9-传感器;10-A/D 转换器;11-放大器;12-计算机(a )频谱(b )功率谱 图4.31 频率特性图【案例4.15】 在内燃机车谐振频率测定、桥梁和各种结构自振频率和振型的测定中,通过功率谱分析振动信号的频率成分和结构。
【案例4.16】 对于一些重要设备,如火箭、飞机和汽轮机以及发动机、齿轮箱等,均可根据功率谱的变化(有否额外谱峰)来判断故障发生的原因,以便迅速排除故障。
【案例4.17】 在研究机械零部件的强度和疲劳寿命时,利用功率谱反映出载荷在各频率成分上的振动能量与振幅,为确定载荷谱提供了条件。
【案例4.18】 在医学上,可根据的检测的脑电波、心电波进行功率谱分析来研究病症及病理。
【案例4.20】模拟信号()()()t t t x ππ8cos 54sin 2+=,以()1~001.0-==N n n t 进行取样,分别求其64=N 和512=N 点DFT 的幅值谱。
