网络层次分析法应用形式的多样性
层次分析法在计算机联网技术中的应用

层 次分 析法是综 合相关 因素 , 进 行合理搭 配 , 实现优化
配 比的最优方案。 层次分析法是由美国人 T . L . S a a t y 最早提 出 来的, A n a l y t i c H i e r a r c h y P r o c e s s 层 次分 析法 的诞 生是 在 最终
性分 析的判 断依 据是根据特征根与特征 向量 的一致性 指标 、
比率及随机 的一 致性指标 、 比率 等 因素进行符合分 析 , 得出
权 向量 的一致性 。 计算项 目的组合权 向量一致性分析主要是
针对项 目的方案层与 目标层 , 如果 得出的结 果与所需部相符
那 么则需要 进行 重新 的成对矩阵分析 比较 , 直至得 出正确 的
2 0 1 3年第 1 5 期
经济研究导刊
EC 0N0MI C RES EARC H GUI DE
No . 1 5, 2 0 1 3
总第 1 9 7 期
S e i ̄ No f . 1 9 7
层次分析法在计算机联网技术中的应用
刘 长 青
( 贺州学 院, 广西 贺州 5 4 2 8 9 9 )
前言
层次分析法应用于计算机组 网技术 中, 具有权衡利弊 , 主 张劝和 , 对组 网因素进行细分 , 合 理的引导计算 机联 网中各
个方面的因素协调配合 , 实现合理联 网 目的。层 次分析法可
层次分 析法分析 的主要方式 与方法是 对要进行 决策 的 问题进行层次化 划分 , 将问题 引入分析模 型 , 通过 比较和权 向量的计 算 , 保证检验一致 。层次 分析 法在 计算 机组 网方案 的制定中 , 具有权衡 因素 、 细化分层 的作用 , 对于计算机联 网
层次分析法在计算机联网技术中的应用

同理建立准则层对方案层 的成对 比较矩 阵 B 具体如下所 ,
示:
i 3 i B2= 2 2 1
/ j
1
/ Z
2 3 4
i 2 3
I 2
B3=
1 1 2, … , , /
19 /
C 与 C的 影 响 之 比 相 反 j
、
进行分析 。 层次分析法的优势在于, 可以将一个 复杂的多 目 它 标决策 问题进行分解、细化 ,从而可 以通过定性 、定量 的方式 将繁琐 的分析处理过程简单化 , 尤其是对一些 目标存 在较 多不 确定性 以及 结构十分复杂 的情况 , 层次分析法能够很好的发挥
出 目身 的 技术 优 势 。
中图分类号 :T 33 3 P9. 0
一
文献标识码 :A 文章 编号 :10- 5921) 6 03— 2 07 99 ( 2 0- 05 0 0
-
无线 电通讯技术划分成方案层 。 而组网过程 中的设备一次性投 层 次 分 析 法 的 概 念 层 次 分 析 法 (n l t cH ea cy P o e s A a y i i r r h r c s )是 2 O世 纪 资 、网络在运营过程中的费用、网络 的性 能、可管理性 以及售 7 年 代 初 期 由 美 国 匹 茨 堡 大 学 教 授 著 名 的 运 筹 学 家 后服务 五大 元素可 以划分 为准 则层 。 0 计算机联 网技术 的选择 为 T L S a y提 出来 的, ..at 主要是指所有与决策有关 的因素划分成 最终的 目标层。层次分析法数 学模 型如 下图 1 示: 所 目标 层、 则层以及方案层, 准 然后通过 定量 与定性相结合方式
诤冀枫飘璃械拳逸棒
多层次关联网络模型在社会网络分析中的应用研究

市中小学教职工年上半年政治理论学习安排1文章标题:市中小学教职工2019年上半年政治理论学习安排市中小学教职工2019年上半年政治理论学习计划2019年,是实施“十一五”规划的开局之年,是全面贯彻落实科学发展观的重要一年。
全市中小学要以邓小平理论和“三个代表”重要思想为指导,紧紧围绕全面贯彻落实科学发展观,深入推进理论武装工作,进一步加强师德建设,通过卓有成效地开展一系列学习教育活动,统一思想,提高认识,促进发展,保持稳定,为实现**教育的跨越式发展提供强大的精神动力和思想保证。
现制订政治理论学习计划如下:一、学习内容第一专题:深入学习党的十六届五中全会精神学习篇目:1、2019年1月1日胡锦涛在全国政协新年茶话会上的讲话(主题:2019年要为“十一五”开好局、起好步)2、2月14日,胡锦涛在省部级主要领导干部建设社会主义新农村专题研讨班开班式上的讲话(主题:扎扎实实规划和推进社会主义新农村建设)3、《中共中央关于制定国民经济和社会发展第十一个五年规划的建议》4、《中共中央关于推进社会主义新农村建设的若干意见》思考题:1、你怎[本文转载自第1-1找文章,到第1]样认识在“十一五”时期开局之年做好改革发展稳定的各项工作的重要意义2、建设社会主义新农村过程中,教育重点应做好几方面工作3、中共中央关于制定十一五规划的建议中对教育事业发展有哪些论述你为十一五期间我国教育事业发展有什么构想或期待你能为十一五期间教育发展做什么第二专题:深入学习贯彻科学发展观学习篇目:1、2019年3月10日胡锦涛在中央人口资源环境工作座谈会上的讲话(主题:科学发展观是我党提出的新重大战略思想)2、中国共产党第十六届中央委员会第五次全体会议公报(2019年10月11日)3、2019年12月21日胡锦涛在北京展览馆参观建设节约型社会展览会时的讲话(主题:贯彻落实科学发展观,加快建设节约型社会)思考题:1、如何认识科学发展观的时代背景、重大意义、科学内涵和精神实质2、胡锦涛在展览会参观时指出当前建设节约型社会要注重抓好哪五项工作你对建设节约型社会有哪些认识3、从贯彻落实科学发展观的高度,谈一谈你对节约能源资源的极端重要性和紧迫性的认识第三专题:加强和改进师德建设学习篇目:1、《教育部关于进一步加强和改进师德建设的意见》(2019年1月13日)2、宁波市教育局《关于进一步加强和改进中小学班主。
层次分析法(AHP)与网络层次分析法(ANP)的比较

层次分析法(AHP)与网络层次分析法(ANP)的比较作者:孙铭忆来源:《中外企业家》 2014年第4期孙铭忆(济南大学,山东济南 250022)摘要:在多目标决策中,层次分析法(AHP)是使用频率较多的研究方法,网络层次分析法(ANP)是对层次分析法的拓展和延伸。
本文在论述层次分析法(AHP)与网络层次分析法(ANP)概念模型的基础上,对比了两种方法在系统模型和判断矩阵构建方面的异同点,为更好地利用这两种决策方法提供理论基础。
关键词:层次分析法;网络层次分析法;系统构建;判断矩阵;方法对比中图分类号:C931文献标志码:A文章编号:1000-8772(2014)10-0067-02著名的经济学家赫伯特·西蒙提出“管理即是决策”,因此,无论是在企业中还是在我们的日常生活中都会遇到大大小小的决策问题[1]。
从宏观层次来看,我们的国家领导人面临着政治、经济、文化和军事等方面的决策,决策的科学与否直接关系到国家的安危和兴旺,关系到整个地区的长治久安;从中观层次来讲,企业的管理者时时刻刻面临着决策问题,大到战略决策、小到生产计划决策,每一个决策都关系到企业的可持续发展;从微观层次来说,每个人也都面临着诸如学习、就业、旅行等日常决策问题,它们会影响到家庭的和谐和个人的发展。
由此可见,正确的决策是各个实体发展的基础。
就决策的方法而言,同一个问题按照不同的方法分析可以得出不同的结论,一方面是因为不同方法在数据处理时的侧重点不同,另一方面是因为选取了不适用的决策方法,得出了具有误导性的结论。
因此,选择适当的决策方法是进行恰当决策的关键所在。
简单的决策方法虽然容易实施,但会因考虑不周等原因导致非常可怕的后果,比如经验主义,拍脑袋决策等,相反,科学的决策方法则能够为我们提供合理的结果,帮助我们做出正确的决策。
对于单目标决策,依靠模型就能够精确地描述问题,其结果也能够通过统计、运筹、计算机等技术得出。
而对于多目标决策,其复杂性明显上升,我们通常会利用层次分析法及网络层次分析法等进行决策分析。
多层次关联网络模型在社会网络分析中的应用研究

多层次关联网络模型在社会网络分析中的应用研究随着社交媒体、在线社区和智能手机应用的普及,社会网络的规模和复杂性不断增加。
社交网络用户之间的联系复杂多样,大量的信息和数据不断产生。
因此,如何有效地分析和理解社交网络对于我们更好地理解和应对社会、政治和经济等方面的问题具有至关重要的意义。
在这种情况下,多层次关联网络模型在社会网络分析中的应用越来越受到关注。
多层次关联网络模型是指一种包含多个层次和维度的网络模型,可以用来描述多个关系和因素之间的相互影响和依赖关系。
相比于传统的社会网络模型,多层次关联网络模型能够更好地反映现实社会网络中的多样性和异质性。
在研究社会网络时,我们可以使用多层次关联网络模型来探究不同社交网络中的关系和联系。
例如,在研究互联网社区时,我们可以将用户之间的联系划分为不同的维度,例如传统社会关系、兴趣爱好、个人价值观等。
这些不同的维度可以用不同的网络层来表示,通过这种方式,我们可以更好地理解和分析互联网社区中用户之间的社交关系以及社区的发展和演化规律。
多层次关联网络模型还可以用来研究社会网络中的信息传播和影响机制。
例如,在分析社交媒体数据时,我们可以将用户之间的信息传播和影响关系划分为不同的维度,例如信息主题、传播路径、用户特征等。
通过这些不同的维度,我们可以构建多层次关联网络模型来分析不同主题和用户之间的影响机制,进而改进信息传播策略和营销方法。
除此之外,多层次关联网络模型还可以用来探究社会网络中的群体行为和演化规律。
在研究社会网络中群体行为时,我们可以将不同的群体和组织划分为不同的网络层,分析不同群体之间的合作、竞争、冲突等行为。
同时,我们还可以通过多层次关联网络模型来分析群体演化的规律以及影响群体演化的因素。
在社会网络分析中,多层次关联网络模型是一种非常有潜力和实用价值的研究方法。
通过搭建多维度、多层次的关联网络模型,我们可以更好地理解和探究社会网络中的联系和关系,为社会网络的管理和应用提供更加有效的支持和指导。
用SuperDecision进行网络层次分析法(ANP)的应用实例
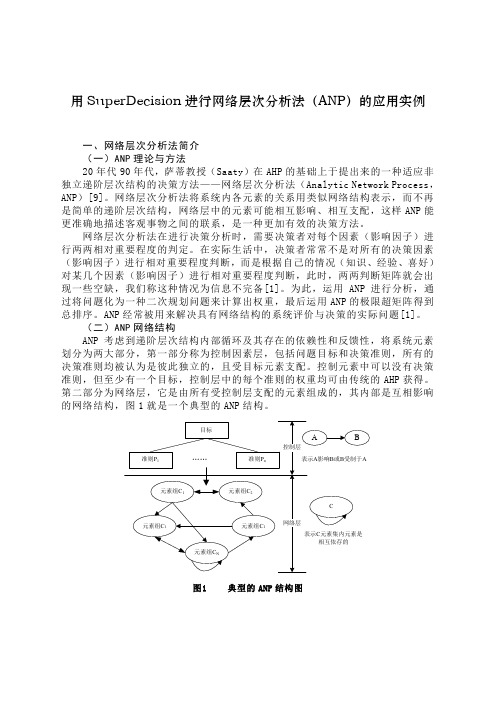
用SuperDecision进行网络层次分析法(ANP)的应用实例一、网络层次分析法简介(一)ANP理论与方法20年代90年代,萨蒂教授(Saaty)在AHP的基础上于提出来的一种适应非独立递阶层次结构的决策方法——网络层次分析法(Analytic Network Process,ANP)[9]。
网络层次分析法将系统内各元素的关系用类似网络结构表示,而不再是简单的递阶层次结构,网络层中的元素可能相互影响、相互支配,这样ANP能更准确地描述客观事物之间的联系,是一种更加有效的决策方法。
网络层次分析法在进行决策分析时,需要决策者对每个因素(影响因子)进行两两相对重要程度的判定。
在实际生活中,决策者常常不是对所有的决策因素(影响因子)进行相对重要程度判断,而是根据自己的情况(知识、经验、喜好)对某几个因素(影响因子)进行相对重要程度判断,此时,两两判断矩阵就会出现一些空缺,我们称这种情况为信息不完备[1]。
为此,运用ANP进行分析,通过将问题化为一种二次规划问题来计算出权重,最后运用ANP的极限超矩阵得到总排序。
ANP经常被用来解决具有网络结构的系统评价与决策的实际问题[1]。
(二)ANP网络结构ANP考虑到递阶层次结构内部循环及其存在的依赖性和反馈性,将系统元素划分为两大部分,第一部分称为控制因素层,包括问题目标和决策准则,所有的决策准则均被认为是彼此独立的,且受目标元素支配。
控制元素中可以没有决策准则,但至少有一个目标,控制层中的每个准则的权重均可由传统的AHP获得。
第二部分为网络层,它是由所有受控制层支配的元素组成的,其内部是互相影响的网络结构,图1就是一个典型的ANP结构。
图1 典型的ANP结构图二、ANP算法步骤(一)分析问题。
将决策问题进行系统的分析、组合形成元素和元素集。
主要分析判断元素层次是否内部独立, 是否存在依存和反馈。
可用会议讨论、专家填表等形式和方法进行。
(二)构造ANP的典型结构。
多层网络分析算法研究与应用

多层网络分析算法研究与应用第一章:引言多层网络分析算法是一种重要的分析方法,可以帮助研究人员深入了解复杂系统的结构与行为。
在过去的几十年中,多层网络分析算法被广泛应用于社交网络、生物网络、交通网络等领域,为我们提供了深入理解这些系统的机会。
本章将介绍多层网络的定义和基本概念,并总结多层网络分析算法的研究进展和应用领域。
第二章:多层网络的定义与基本概念2.1 多层网络的定义多层网络是由多个网络层次组成的复杂网络,每个网络层次表示系统中的一个特定的关联关系。
多层网络通过多个网络层次之间的连接,模拟和描述了复杂系统的多个方面。
多层网络的定义不仅包括网络的节点和边,还包括网络层次之间的连接关系。
2.2 多层网络的基本概念在多层网络中,节点表示系统的个体或元素,边表示节点之间的关联关系。
网络层次之间的连接可以是同一节点在不同层之间的连接,也可以是不同节点之间的跨层连接。
多层网络的基本概念包括节点的度、度分布、聚类系数、介数中心性等。
第三章:多层网络分析算法的研究进展3.1 多层网络的可视化与摘要多层网络的可视化与摘要是多层网络分析中的重要环节。
传统的二维网络可视化方法不能直观地展示多层网络中的层次结构和跨层连接。
因此,研究人员提出了多种多层网络的可视化方法,如Monya、MULTIPLEXVIS等。
这些方法可以有效地展示多层网络的结构和特征。
3.2 多层网络的社区发现社区发现是多层网络分析的核心任务之一。
多层网络的社区结构可以帮助研究人员发现节点之间的模式和关联关系。
传统的单层网络社区发现算法不能很好地应用于多层网络,因为多层网络中的节点有多个层次的关联关系。
因此,研究人员提出了多层网络的社区发现算法,如MOM、MCLA等。
3.3 多层网络的节点中心性节点中心性是衡量节点在网络中的重要性的指标。
在多层网络中,传统的节点中心性算法无法直接应用于多层网络的节点。
因此,研究人员提出了多层网络的节点中心性算法,如多层PageRank算法、多层介数中心性等。
多层网络分析算法研究与应用

多层网络分析算法研究与应用摘要:多层网络分析算法是一种基于网络结构的分析方法,通过对网络中的多层关系进行建模和分析,可以揭示出网络中的隐藏信息和模式,对于解决复杂问题具有重要意义。
本文首先介绍了多层网络的概念和特点,然后综述了当前常用的多层网络分析算法,并对其进行了比较和评价。
最后,通过实际案例研究,展示了多层网络分析算法在实际应用中的价值和潜力。
关键词:多层网络;分析算法;建模;隐藏信息;复杂问题1. 引言随着互联网的快速发展和各种社交媒体平台的兴起,人们之间产生了大量复杂而庞杂的关系。
这些关系可以用图论中的图结构来表示,并且往往是具有多个维度或者层次结构。
传统上常用单一维度或者单一视角来研究这些关系,然而这种方法往往无法揭示出隐藏在底层数据之下的更深入信息。
因此,在解决复杂问题时需要引入更加强大且适用的分析方法。
多层网络分析算法就是一种基于网络结构的分析方法,可以对多层关系进行建模和分析,从而揭示出隐藏的信息和模式。
2. 多层网络的概念和特点多层网络是一种具有多个维度或者层次结构的复杂关系网络。
它可以用一个多维矩阵来表示,其中每个维度或者层次对应一个特定类型或者关系。
例如,在社交网络中,可以将用户之间的社交关系、兴趣关系、地理位置等信息作为不同维度或者层次来表示。
多层网络具有以下特点:2.1 多维度:每个维度对应一个特定类型或者关系,可以从不同角度来描述复杂系统。
2.2 多模态:每个模态对应一个不同类型的数据,在建模时需要考虑数据之间的相互作用。
2.3 多尺度:每个尺度对应一个不同级别的结构,可以从宏观到微观进行分析。
3. 常用多层网络分析算法目前已经有许多针对多层网络的分析算法被提出,并且在各个领域得到了广泛应用。
以下是几种常见且经典的算法:3.1 多层网络聚类算法:该算法通过将多层网络转化为单层网络,然后利用传统聚类算法进行分析,可以将多层网络中的节点进行聚类。
3.2 多层网络社区发现算法:该算法通过考虑多个维度或者层次的信息,可以发现多个社区结构,并且揭示出不同维度或者层次之间的关联。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
The S tud ies on th e App lication D iversity of ANP
WANG Juan, L I H ua
( School of Econo m ics and M anagemen t , X id ian University, X i. an 710071 , Ch ina) Abstrac t : A na lytic ne t w ork pro cess ( AN P) is one o f mo st ex tre m e ly effective m ethods in the dec isionm aking m anage m ent and the modern achiev e m ents appra isa.l It obta ins the w idespread applica tion and the rap id pro m otion in forecast , p lan and potency deter m ined and conflict ana ly sis and so on . T his paper m a in ly ai m ed at the d ive rsity ana lysis of ANP wh ich ex isted in its application. T hrough compar ing the characteristic ofAN P m a trix , we ob tain differentm anifestation o f m atr ix under the d ifferen t conditions . It prov ides the foundation fo r us to so lve various AN P prob lem s . K ey word s : ANP; compared ma tr ix ; d iversity
, 应急桥梁设计方案评估
[ 4, 5 ]
[ 3]
, 以及在供应链管
理中的应用
, 等等。然而 , 大多数 文献采用了
ANP最初的应用形式 , ANP 的应用存在一种模式 化的现象。 本文主要针对变化条件下 ANP 的应用进行了 研究, 比较全面地分析了 ANP 应用中的变化情况 及不同变化情况下 ANP 所采取的不同形式, 使得 ANP的应用更加切 近于客观实际, 也 使得其应用 范围更加广泛。
E
n
2 a i3 + n - 2
i= 1
事实证明, 该结果对于一致性和非一致性判断矩阵 都是可行且有效的。 对于现实世界另 外一些特殊 情况
[ 9]
, 比如说
在比赛中 A 战胜了 B, B 战胜了 C, 而 C 又战胜了 A, 显然判断 本身不具有一致性。因此 , 如果仅用 这一种正互反矩阵来表示判断 , 许多时候就可能会 与现实相悖。我们需要更多新的形式的判断矩阵, 如下面的矩阵 P 表示一种具有循环判断的矩阵形 式 , 其一致性检验 CR = 1 . 2821> > 0 . 1 , 不符合通 # 66#
1 引言 网络 层 次 分 析 法 ( Analyt ic netw ork process , ANP) 是美国 运筹学家 Saaty 于 1996 年正 式提出 的。它不仅保留了层次分析法的优点 , 又是层次分 析法的进一步扩展, 是解决复杂结构问题的一种有 效方法。最近几年, ANP 逐渐被人们所重视 , 并且 在经济、 管理以及技术领域 , 得到广泛应用 , 尤其在 各种评价工作中发挥了不可替代的作用。如对大 [ 1] 型基础设施项目计划的综合 评估 , 网络安全评 估
[ 2]
2 ANP 应用形式的变化 根据不 同问题或 相同问 题的 不同背 景, ANP 的应用形式是在不断发生变化的, 如图 1 所示。 图 1 左侧反映的是 ANP 应用的整个流程
[ 6]
,
右侧则反映了随流程进展 ANP 变化的应用形式。 在第一步确立了群组、 准则以及决策方案等的内部 因素之后, 第二步便是要建立这些内部因素之间的 关系 , 这里存在模块关系变化以及要素关系变化 , 不同的关系变换具有不同的表达形式。在第三步 建立各组成成分的两两比较矩阵时 , 根据不同的数 据来源, 任意两两要素进行比较时会产生不同的矩 阵形式。当 两者关系可以用精确的数据表示 ( 精 确判断 ) 时, 比较矩阵可直接建立 ; 当两者之间关 系需要通过专家的主观经验判断 ( 模糊判断 ) 来实 现时 , 便产生了比较矩阵的绝对标度和区间标度两 种不同的情况。在第四步获取参与比较的要素的 重要性权重的同时, 还要对此两两判断矩阵进行一
i= 1
- (a21 + a12 ) + ,,
Ea
i= 1
n
2 i2
+ n - 2- , - (a2n + an2 )ຫໍສະໝຸດ W + Ke= 0
- (an1 + a1n ) - ( an 2 + a2n ) - , +
Ea
i= 1 T
n
2 i3
+n- 2
e= ( 1 , 1, 1) 上述 eW = 1 , 两式联立 , 可求出权重的向量 * - 1 T - 1 W = B e /e B e
图 2 输入输出网 络
例如, 图 2 表示一个系统内部部门之间以及与 其外部市场之间的资源 ( 信息等 )输入输出的网络 关系图。已知系统内部部门之间的资源输入输出数 量 x ij (x ij表示部门 i向部门 j 的资源输出量 ), 外部市 场对系统内部资源的需求 d i (d i 表示外部市场对系 统内部部门 i的资源需求量 )以及系统外部市场给 系统内部带来的价值增值 vj ( vj 表示对于部门 j 的价 值增加 ), 便可以建立以下 n + 1维矩阵 Sectors S1 S 1 x 11 S 2 x 21 , , Sn x n1 v1 S2 x 12 x 22 , x n2 v2 , , , , , , Sn x 1n x 2n , x nn vn d1 d2 , dn
Ea
i= 1
n
2 i 1 + n - 2 - (a 12 + a 21) - , - (a 1n + an 1)
其中
B =
- (a 21 + a 12 ) + ,,
Ea
i= 1
n
2 i2 + n - 2 - , - (a 2n + a n2)
- (an1 + a 1n ) - (a n2 + a 2n ) - , +
预
测
2007年第 6 期
此时 CR < 0 . 1 不成立 , 那么在满足完全一致 性条件下成立的方程组 W i = aijW j
常的判断形式。所以在这里可以采用最小平方法 判断各因素的相对重要性权重 1 3 1 /3 P = 1 /3 1 3 3 1 /3 1 利用最小平方法可得 T 40 40 40 B= 9 9 9 * -1 T - 1 W = B e /e B e 于是在不进行更多比赛的情况下, 可以简单判断得 到, A、 B、 C 同样重要。 4 ANP 判断矩阵表达形式多样性分析
E
n
i, j = 1 , 2 , ,, n
[ 8]
Wi = 1
i= 1
将不恒成立。 为此可以引入权的最小平方法 : 令 eij = W i - aijW j; i, j = 1 , 2 , ,, n, 由于 eij 不 为零, 所以可以选择合适的向量 W 使 eij 的平方和 最小, 即 m inJ =
图 1 AN P 的基本步骤及应用中的变化
3 ANP 中模块关系以及要素关系多样性分析 ANP中模块关系的变化主要体现在整体的结 构模型的变化上 , 我们有内部独立的递阶层次结构 模型, 内部依存的递阶层次结构模型 , 内部独立的 循环结构模型以及内部依 存的循化结构 模型
[ 7]
起作用, 效用理论认为 : 若 A 优于 B, B 优于 C, 那 么 A 一定更优于 C, 例如 , 我们假设在某一准则下 A、 B、 C 三个要素间比较关系为 : ( 应用 1~ 9 标度 法 )A 比 B 稍微重要 , B 比 C 稍微重要 , A 比 C 明显 重要 , 那么一致性分析结果为: CR = 0 . 0370< 0 . 1 , 此结果已符合要求。也可以通过适当调整, 使其变 得更优。 但在现实中由于判断矩阵的获得都是由专家 给定的, 就必然受到专家知识结构、 判断水平、 个人 偏好的影响 , 加之判断事物本身的模糊性和不确定 性, 就可能导致判断矩阵很难满足一致性的条件 aik aij = , i, j, k = 1 , 2 , ,, n ajk # 65#
n
E E E E
n n
n
n
e =
2 ij
i= 1 j = 1
E E
n
n
(W i - a ijW j )
2
i= 1 j = 1
由于 E W i = 1 , 作拉格朗日函数
i= 1
L (W, K ) =
n
i= 1 j = 1
(W i - aij W j ) + 2K( E W i - 1)
2 i= 1
n
,
不同的结构模型有不同矩阵表达形式。通常, 一般 的网络结构总可以经过简化而转化成上述情形之 一来处理。 考虑具体要素间关系的变化情况。在元素的 关系比较中 , 最常使用的形式是正互反矩阵。但在 运算时 , 此矩阵是要求具有一致性规范的特点的, ( 本意是使专家的判断有效 ), 即效用理论在其中
Vo1 . 26 , No. 6
一般情况下, 假设部门之间及与外部环境之间的 输入输出是平衡的, 这种假设是符合系统相互影响的 平衡性的。令每个部门的总输入为 I j =
