惯性技术课件4--单自由度陀螺 (哈工大版,1-16全)
合集下载
陀螺ppt课件完美版

2. 观察陀螺进动现象时,可 以通过改变外力矩的大小和方
向来探究其影响。
3. 实验结束后,要及时关闭 电源并拆卸器材,整理实验场
地。
07 总结回顾与展望 未来
关键知识点总结回顾
陀螺仪基本原理
陀螺仪是一种基于角动量守恒原理的装置,用于测量或维持方向 。
陀螺仪的种类与应用
介绍了不同类型的陀螺仪(如机械陀螺仪、光学陀螺仪等)及其 在各领域(如航空、导航等)的应用。
为转子提供稳定的驱动电流, 使转子保持恒定的旋转速度。
信号处理电路
对陀螺仪输出的信号进行放大 、滤波、解调等处理,得到所
需的角速度或角度信息。
典型陀螺仪结构剖析
单轴陀螺仪
仅有一个敏感轴,用于测量绕该轴的 角速度或角度。
双轴陀螺仪
三轴陀螺仪
具有三个相互垂直的敏感轴,可同时 测量绕这三个轴的角速度或角度,广 泛应用于航空航天、导航等领域。
带宽
描述陀螺仪输出信号中随机误差的大小, 通常用单位时间内输出信号的标准差来表 示。
指陀螺仪能够准确测量的角速度范围,通常 以赫兹(Hz)为单位表示。
03 陀螺力学特性分 析
力学基础知识回顾
01
02
03
牛顿运动定律
阐述物体运动与力的关系 ,是分析陀螺运动的基础 。
动量守恒定律
陀螺在不受外力作用时, 其动量保持不变。
03
结合硬件和软件补偿方法,对陀螺仪进行更为全面的误差补偿Biblioteka 。提高测量精度策略
选择高精度陀螺仪
在选购陀螺仪时,应优先考虑精度等级高、 稳定性好的产品。
优化安装环境
为陀螺仪提供稳定的工作环境,减小外部因 素对测量精度的影响。
定期校准
惯性技术课件2 --陀螺力学基础(哈工大版,1-16全)教材

x1 X
z1 Z
y1 Y cos Z sin
z1 Y sin Z cos
Z cos
或 x1 1
y1
0
0
cos
0 X
sin
Y
y1
Y cos
Z sin
Y
z1 0 sin cos Z
X x1
Y sin
Lecture 2 -- Mechanical Fundmentals
R
d~R dt
R
d~ 2 R dt 2
d~ R
dt
2 d~R
dt
( R)
Ar
Ae
相对 牵连切向
Ak
苛氏
Ane
牵连法向
Lecture 2 -- Mechanical Fundmentals
18
3.5*苛氏加速度: 示例
~
Ak
2
dR dt
相对运动 -- 沿径向向外
牵连运动 -- 圆盘的转动
0 X 1 0 X
y
0
1
0
0
cos
sin
Y
0
1
Y
z sin 0 cos 0 sin cos Z 1 Z
(小角度近似)
Lecture 2 -- Mechanical Fundmentals
12
Outline
关于地球 相关的坐标系和坐标变换 柯氏定律和柯氏加速度 动量矩定理
则
d~B
dBx
i
dBy
j
dBz
k
dt dt dt dt
i jk
B x y z
Bx By Bz
Lecture 2 -- Mechanical Fundmentals
惯性技术课件16--振动陀螺(哈工大版,1-16全)概要

苛氏惯性力 m Fc ac mx mn cos n t 2
Lecture 15 -- Vibratory Gyro
9
2.5 动态方程
苛氏惯性力矩
T
T 2sFc 2(s0 x) mxmn cos n t 2ms0 xmn cos n t Tm cos n t
Vibratory Gyro
振动陀螺
Lecture 15 -- Vibratory Gyro
1
Outline
1. 振动陀螺概述 2. 音叉陀螺 3. MEMS 陀螺
4. 半球谐振陀螺
Lecture 15 -- Vibratory Gyro
2
1.1 振动陀螺: 概述
机械陀螺 转子陀螺 ---- 基于牛顿运动定律 ---- 液浮,静电 ---- 结构复杂、昂贵 振动陀螺: 原理 ---- 利用振动的质量随着基座旋转 时产生的苛氏加速度
读取
下底座
Lecture 15 -- Vibratory Gyro
23
4.4 组成
上底座
力发生器: 环形和离散 环形提供能量
离散力发生 器 读取电极
离散力发 生器 环形力 发生器 半球谐振子
离散提供振型 16 个离散电极 读取: 电容式 8 个电极
读取
下底座
谐振子
敏感振型偏转 抽真空,大时间常数
椭圆 1
②
圆 ③
Lecture 15 -- Vibratory Gyro
27
4.7*振型偏转解释(1) 圆椭圆1
v
各位置的速度
Fc
各位置的苛氏惯性力
质量环原来的变形趋势 苛氏惯性力作用下质量 环的变形趋势 上述两种趋势的综合
Lecture 15 -- Vibratory Gyro
9
2.5 动态方程
苛氏惯性力矩
T
T 2sFc 2(s0 x) mxmn cos n t 2ms0 xmn cos n t Tm cos n t
Vibratory Gyro
振动陀螺
Lecture 15 -- Vibratory Gyro
1
Outline
1. 振动陀螺概述 2. 音叉陀螺 3. MEMS 陀螺
4. 半球谐振陀螺
Lecture 15 -- Vibratory Gyro
2
1.1 振动陀螺: 概述
机械陀螺 转子陀螺 ---- 基于牛顿运动定律 ---- 液浮,静电 ---- 结构复杂、昂贵 振动陀螺: 原理 ---- 利用振动的质量随着基座旋转 时产生的苛氏加速度
读取
下底座
Lecture 15 -- Vibratory Gyro
23
4.4 组成
上底座
力发生器: 环形和离散 环形提供能量
离散力发生 器 读取电极
离散力发 生器 环形力 发生器 半球谐振子
离散提供振型 16 个离散电极 读取: 电容式 8 个电极
读取
下底座
谐振子
敏感振型偏转 抽真空,大时间常数
椭圆 1
②
圆 ③
Lecture 15 -- Vibratory Gyro
27
4.7*振型偏转解释(1) 圆椭圆1
v
各位置的速度
Fc
各位置的苛氏惯性力
质量环原来的变形趋势 苛氏惯性力作用下质量 环的变形趋势 上述两种趋势的综合
惯性技术课件3-1 --二自由度陀螺(哈工大版,1-16全).

2
改写方程
M x1( s)
1 J xs2
Hs Hs
( s)
1 M x1 (s) Hs (s) 2 (s) J xs
1 M y ( s) Hs ( s) ( s) 2 J ys
M y ( s)
1 J y s2
(s)
Lecture 3 -- Gimbaled Gyro - 2DOF
22
5.1 建模: 工程参数
z Z
o
d x Jx H y M x dt d y Jy H x M y dt
y
y
框架坐标系中
x1
x , y , M x , M y 是表示在内
x
x
和沿着框架轴的力矩 , 工程中, 使用框架角变化 M x1, M y 来表示转子轴方向及其转动控制会更方便:
27
5.3 模型: 传递函数
根据
J x s 2 ( s) Hs ( s) M x1 ( s) J y s 2 ( s) Hs ( s) M y ( s)
H ( s) M x1 ( s) M y ( s) 2 2 2 2 JxJ ys H s( J x J y s H ) Jx H ( s) M y ( s) M x1 ( s) 2 2 2 2 JxJ ys H s( J x J y s H ) Jy
Lecture 3 -- Gimbaled Gyro - 2DOF
20
5.1 建模: 苛氏定律
其中相对变化率
~ d y ) d x dH d ( z Jx i Jy j Jz k dt dt dt dt
i
牵连变化率
改写方程
M x1( s)
1 J xs2
Hs Hs
( s)
1 M x1 (s) Hs (s) 2 (s) J xs
1 M y ( s) Hs ( s) ( s) 2 J ys
M y ( s)
1 J y s2
(s)
Lecture 3 -- Gimbaled Gyro - 2DOF
22
5.1 建模: 工程参数
z Z
o
d x Jx H y M x dt d y Jy H x M y dt
y
y
框架坐标系中
x1
x , y , M x , M y 是表示在内
x
x
和沿着框架轴的力矩 , 工程中, 使用框架角变化 M x1, M y 来表示转子轴方向及其转动控制会更方便:
27
5.3 模型: 传递函数
根据
J x s 2 ( s) Hs ( s) M x1 ( s) J y s 2 ( s) Hs ( s) M y ( s)
H ( s) M x1 ( s) M y ( s) 2 2 2 2 JxJ ys H s( J x J y s H ) Jx H ( s) M y ( s) M x1 ( s) 2 2 2 2 JxJ ys H s( J x J y s H ) Jy
Lecture 3 -- Gimbaled Gyro - 2DOF
20
5.1 建模: 苛氏定律
其中相对变化率
~ d y ) d x dH d ( z Jx i Jy j Jz k dt dt dt dt
i
牵连变化率
单自由度陀螺运动分析
载体相对惯性空间的转动
j J k H J x xb i J y z H xi H y j H z k
单自由度陀螺运动方程:推导化简
根据动量矩定理
~ dH d H H dt dt
考虑到β非常小,
i
H xb J x xb
2、积分陀螺的阶跃响应 传递函数
HG / c ( s) xb ( s) s(s 1)
输出函数
H G / c xb ( s) s(s 1) s H G xb 1 1 2 c s ss 1 /
H G xb (t ) [t (1 e )] c t
整理得
传递函数:积分+惯性环节 稳态响应:β正比于输入的积分 积分陀螺
Jy HG s s 1 ( s ) ( s ) xb c c
令τ=Jy / c,得到
惯性环节:τ的大小选取
3、当 c=0,k=0,得到
HG ss 1 ( s) xb ( s) c
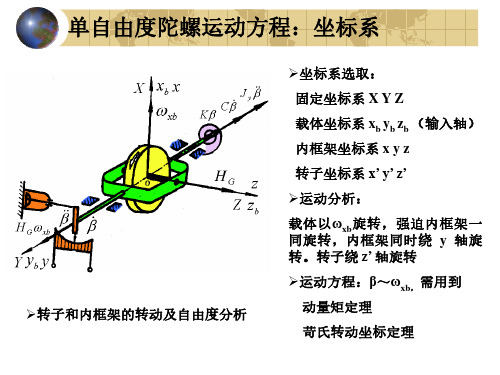
单自由度陀螺运动方程:坐标系
坐标系选取:
固定坐标系 X Y Z
载体坐标系 xb yb zb (输入轴) 内框架坐标系 x y z
转子坐标系 x’ y’ z’
运动分析: 载体以 ωxb 旋转,强迫内框架一 同旋转,内框架同时绕 y 轴旋 转。转子绕 z’ 轴旋转 运动方程:β~ωxb,需用到 转子和内框架的转动及自由度分析 动量矩定理 苛氏转动坐标定理
2
系统输入
' 1
xb ( s)
系统输出
1 2 tg 1
以…为稳定位置的衰减的振荡
(2024年)陀螺课件(61)(共63张PPT)pptx

机械陀螺仪
光学陀螺仪
结构简单、成本低廉,但精度和稳定性较 差,易受环境因素影响。
基于光学原理工作,具有高精度、高稳定 性等优点,但成本较高。
微机械陀螺仪
激光陀螺仪
采用微机械加工技术制造,具有体积小、 重量轻、成本低等优点,但精度和稳定性 相对较低。
利用激光干涉原理测量角速度,具有高精 度、高稳定性、无机械磨损等优点,但成 本较高且对环境要求较高。
多传感器融合与校准
03
在实际应用中,单一陀螺仪往往难以满足需求,多传感器融合
与校准技术成为提高系统性能的关键。
25
探讨未来发展趋势和前景
2024/3/26
新型陀螺仪技术
随着科技进步,新型陀螺仪技术(如量子陀螺仪、生物陀螺仪等)有望在未来取得突破, 为高精度测量和导航领域带来革命性变革。
多源信息融合与智能算法
通过融合多种传感器信息和采用智能算法,可以提高陀螺仪系统的整体性能,实现更高精 度的姿态测量和导航定位。
拓展应用领域
随着陀螺仪性能的不断提升和成本的降低,其应用领域将进一步拓展,如智能交通、智能 家居、虚拟现实等。
26
感谢您的观看
THANKS
2024/3/26
27
组合导航算法
将惯性导航系统与卫星导航系统、里程计等其他导航手段进行组合, 实现优势互补,提高整体导航性能。
14
04
陀螺仪在姿态控制中应用
2024/3/26
15
姿态控制概述及分类
2024/3/26
姿态控制定义
通过对物体姿态的调整,实现其在空间中的稳定定位和定向 。
姿态控制分类
根据控制对象的不同,可分为刚体姿态控制和柔性体姿态控 制;根据控制方法的不同,可分为开环控制和闭环控制。
陀螺及惯性技术课件

陀螺仪在神经科学中的研究进展
陀螺仪在神经科学研究 中的作用和意义
介绍神经科学研究中陀螺仪的 应用和意义。
神经元连接性研究
讲解神经元连接性的概念和研 究方法,并阐述陀螺仪在神经 元连接性研究中的应用。
脑活动成像技术
介绍脑活动成像技术的概念和 原理,讲解陀螺仪在脑活动成 像技术中的应用。
深度探讨惯性传感器
2
加速度计原理
讲解加速度计原理,并探讨加速度计在压力传感器中的应用。
3
实验验证
通过实验验证,证明加速度计在微电子压力传感器中的应用效果。陀螺仪惯性导航系统对无人机姿控制 的应用陀螺仪原理
介绍陀螺仪的原理和分类, 并阐述其在空中姿态控制中 的重要性。
惯性导航系统原理
讲解惯性导航系统的原理和 组成,并探讨其对无人机飞 行中的支持作用。
无人机姿态控制
分析无人机姿态控制的难点 和挑战,并探讨陀螺仪惯性 导航系统在其中的应用。
惯性导航系统在导弹制导中的应用
导弹制导概述
介绍导弹制导的基本概念和分类,探讨惯性导航系统在其中的应用。
惯性测量单元
阐述惯性测量单元的组成和原理,并表明其在导弹制导中的重要作用。
导弹姿态控制
分析导弹在飞行过程中的姿态控制难点,探讨惯性导航系统在其中的应用。
MEMS技术
介绍惯性传感器中的MEMS技术,讲解其应用 和成果。
光纤陀螺
讲解光纤陀螺的原理和优点,探讨其在惯性传 感器中的应用前景。
陀螺及惯性技术课件
本课件将介绍陀螺和惯性技术的原理及其在不同领域的应用。通过本课件的 学习,您将对陀螺及惯性技术有更深入的了解。
导言
本章节将引入陀螺及惯性技术的主题,并简述陀螺和惯性技术对现代工程的 作用和重要性。
工学陀螺及惯性技术课件PPT56页

Kg
0
0 cos0t 0 Kg
T 2 1 84.4 min
Kg
1 R K
第54页,共56页。
舒拉调整平台
0 cos0t 0 Kg
T 2 1 84.4 min
Kg
1 R K
用积分陀螺代替积分器:
H R K
第55页,共56页。
作业
P117-1,2,5,7,8
第56页,共56页。
尺寸
重量
转速
动量矩H
阻尼系数C 输出轴惯量J
Ф4.6×9.8cm 522 gf
24000 r/min 151000
502 225
G(s)=1, C2=5, τ=1ms
SystemView仿真结果
第19页,共56页。
单轴平台系统方块图之二
Y (s)
JP J s4
JP (J
( s 1)(Js C) C)s3 (JPC H 2 )s2
二自由度陀螺仪平台的方程
K K1K2Kt H
K K2Kt H
K3 (s)
J ps2 KG(s) KG(s)
{s 2 [ J
ps2
KG(s)]
K
K1K2Kt K3 (s)KG(s)g }
HR
(s)
0
{s2[
J
p
s2
KG(s)]
(J
p
s
2
KGபைடு நூலகம்s))
g }
R
(s)
0
{(s2
g )[J R
ps2
(11s)(1 2s)K
JPs2 (1 T1s)(1 T2s)
第36页,共56页。
5.4 半解析式惯导系统的修正回路
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2
1.0*单自由度陀螺: 介绍
x X
单自由度(1-DOF) 陀螺: 结构 -- 只有一个框架
转子轴的自由度 – 仅一个
H
y
z
转子轴绕着 x-轴方向缺少转动自由度 转子轴不具有稳定性
Lecture 4 -- Gimbaled Gyro - 1DOF
3
2.0 敏感轴
X x
MX
当基座绕着 x-轴旋转: 转子轴被迫也绕着 x-轴旋转;
zb yb
T
xb
S
M
G (S )
Lecture 4 -- Gimbaled Gyro - 1DOF
25
End
Lecture 4 -- Gimbaled Gyro - 1DOF
26
Single Degree-of-Freedom gyro
单自由度陀螺仪
Lecture 4 -- Gimbaled Gyro - 1DOF
1
Outline
单自由度陀螺介绍 单自由度陀螺动力学建模 单自由度速率陀螺和积分陀螺 应用示例: 平台单轴稳定
Lecture 4 -- Gimbaled Gyro - 1DOF
记
MB B HG
H G (xb B )
上式意味着,给单自由度陀螺仪施加控制力矩,效果 上等同于施加了相当幅值的输入角速率.
Lecture 4 -- Gimbaled Gyro - 1DOF
23
Outline
单自由度陀螺介绍 单自由度陀螺动力学建模 单自由度速率陀螺和积分陀螺 应用示例: 平台单轴稳定
x
xb
xb
yb
y
HG z
zb
J k H J xxb i J y j z
Lecture 4 -- Gimbaled Gyro - 1DOF
13
3.4 建模: 动量矩
转子的动量矩:
x
J k H J xxb i J y j z
i
H xb J x xb
j J y
~ dH J xxb i J y j J z k dt
Lecture 4 -- Gimbaled Gyro - 1DOF
15
3.5*模型: 力矩
x
因为我们只关心 β 角的变化规律, 所以只需 要抽取沿着 y-轴的分量,得到
根据动量矩定理和苛氏定律:
xb
xb
HG z
~ dH d H H M dt dt
其中
yb
y
zb
xb i j
Lecture 4 -- Gimbaled Gyro - 1DOF
14
3.4*建模: 动量矩
~ dH d H H M dt dt
11
3.3 建模: 转动
x
xb xb cos i xb sin k
内框架相对惯性空间的转动角 速度:
xb
xb
yb
y
HG z
r xb
xb cos i j xb sin k xb i j —— 对小角度
Lecture 4 -- Gimbaled Gyro - 1DOF
19
3.1*速率陀螺
单自由度陀螺义的分类 (基于 c 和 k )
1、当 c≠0,k≠0 系统时域方程
频域拉氏变换
J y c k H G xb
(s)(J y s 2 cs k ) HGxb (s)
Jy HG 改写为 s s 1 ( s) xb ( s) c c HG 记 J y / c ,得 ss 1 ( s) xb ( s) c HG / c ( s) 传递函数 xb (s) s(s 1)
包括:积分环节 + 一阶惯性环节
转子坐标系 -- x' y' z'
Lecture 4 -- Gimbaled Gyro - 1DOF
9
3.2 建模: 任务和方法
xb X x
xb
任务: 建立输出转角 β 和输入 角速度 ωxb,之间的关系
yb Y
y
HG z zb Z
途径: 动量矩定理 + 苛氏定律
Lecture 4 -- Gimbaled Gyro - 1DOF
内框架也被迫以角速度ωxb 绕 x-轴转动
同时,内框架也以角速度 绕 y-轴转动
Lecture 4 -- Gimbaled Gyro - 1DOF
8
3.1 建模: 坐标系
xb X x
xb
坐标系: 固定坐标系 -- XYZ
yb Y
y
HG z z轴 xb ) 内框架坐标系 -- xyz
zb
Lecture 4 -- Gimbaled Gyro - 1DOF
12
3.3 建模: 转动
内框架角速度: xb i j 转子相对惯性空间的角速度: ' k xb i j k 转子的动量矩:
xb
xb
J y J zxb M y
或 其中
J y H G xb M y
yb
y
HG z
zb
M y Mc Mk M B M f
Lecture 4 -- Gimbaled Gyro - 1DOF
16
3.5*模型: 力矩
J y H G xb M y
转子将绕着内框架轴 y-轴进动
H z
F
F
y
结论: 单自由度陀螺能够敏感基座 绕着其转子轴缺少转动自由度的 方向的转动。
Lecture 4 -- Gimbaled Gyro - 1DOF
5
1.2 Product - JG7005
Internal view
In package
Lecture 4 -- Gimbaled Gyro - 1DOF
典型的 II 阶系统,可以改写为
2 2 H / J n n G xb y
其中
c 2 J yk
n
k Jy
等效阻尼比
自由振荡频率
Lecture 4 -- Gimbaled Gyro - 1DOF
18
Outline
单自由度陀螺介绍 单自由度陀螺动力学建模 单自由度速率陀螺和积分陀螺 应用示例: 平台单轴稳定
Lecture 4 -- Gimbaled Gyro - 1DOF
24
5.0 应用例子: 平台稳定与跟踪
一个单轴平台,利用单自由度陀螺仪进行稳定
H G xb (t ) t 作为反馈给电机 c 若要控制平台旋转,可施加控制 力矩 H M (t ) G xb t B t c c HG MB ( xb )t c HG MB 当 得到 xb (t ) 0 HG
10
3.3 建模: 转动
选取内框架坐标系作为动坐标系 内框架相对基座的转动角速度:
x
xb
xb
r j
基座相对惯性空间的转动角 速度:
yb
y
HG z
xb xb cos i xb sin k
zb
Lecture 4 -- Gimbaled Gyro - 1DOF
HG ( s) xb ( s) J y s 2 cs k
HG xb k
称为速率陀螺(rate gyro)
传递函数
稳态时
Lecture 4 -- Gimbaled Gyro - 1DOF
20
3.2*积分陀螺
2、当 c≠0,k=0, 有
J y s 2 (s) cs (s) H G xb (s)
HG xbdt c
Lecture 4 -- Gimbaled Gyro - 1DOF
22
3.3 控制力矩输入的影响
仅角速率输入 外加控制力矩输入
J y c HGxb J y c HGxb M B
H G xb H G MB HG
Lecture 4 -- Gimbaled Gyro - 1DOF
21
3.2 积分陀螺稳态响应
HG / c ( s) xb (s) s(s 1)
稳态响应:
s ( s) H G / c xb ( s) s 1
HG xb c
—— 积分陀螺
HG xb c
其中
xb x
M y Mc Mk M B M f M c c (阻尼) M k k (扭转弹簧)
-- 控制力矩 -- 干扰力矩
xb
k
c
MB Mf
故
yb y
HG z zb
忽略 M f , 得到
J y HGxb c k M B
J y c k HGxb M B
Lecture 4 -- Gimbaled Gyro - 1DOF
17
3.6 模型: II 型系统
J y c k HGxb M B 忽略控制力矩 M B , 得 J y c k HGxb
6
Outline
单自由度陀螺介绍 单自由度陀螺动力学建模 单自由度速率陀螺和积分陀螺 应用示例: 平台单轴稳定
