偏微分方程.ppt
合集下载
偏微分方程数值解_图文_图文

估计误差
这种误差称为“局部截断误差”,如图。
局部截断误差是以点 的精确解 而产生的误差。
为出发值,用数值方法推进到下一个点
2.整体截断误差—收敛性
整体截断误差是以点 的初始值 为出发值,用数值方法推进i+1步到点
,所得的近似值 与精确值
的偏差:
称为整体截断误差。
特例,若不计初始误差,即 则
即 3.舍入误差—稳定性
五、线性多步(Linear Multistep Method)法
1. 预备知识:插值多项式
插值是离散函数逼近的重要方法,利用它可通过函数在有限个点处的取值状况, 估算出函数在其他点处的近似值。
从几何上理解:对一维而言,已知平面上n+1个不同点,要寻找一条n次多项式 曲线通过这些点。插值多项式一般常见的是拉格朗日插值多项式。
把
代入 中,有
经比较得到
取 为自由参数: 从而得到不同的但都是二阶的R-K方法,对应的有中点法、Heun(亨)法 以及改进的Euler法。
基于相同的过程,通过比较五次Taylor多项式,得到更加复杂的结果,给出了包含 13个未知数的11个方程。得到多组系数,其中常用的是以下四阶R-K法:
改进的Euler法、R-K法以及解析解的比较:
是待定的系数。
Euler法就是
的R-K法。
其系数的确定如下:将 展开成 的幂级数,并与微分方程的精确解
在点 的Taylor展开式相比较,使两者的前
项相同,这样确定的R-K法,
其局部截断误差为
,根据所得关于待定系数的方程组,求出它们的值后
代入公式,就成为一个 阶R-K方法。
例题 以二阶R-K法为例说明上述过程
2. Curtis F.Gerald and Patrick O., Applied Numerical Analysis, Person Education, Inc., 2004.
《常微分方程》第7章 一阶线性偏微分方程ppt课件

2021-5-10
7
xi' fi (t, x1,, xn ) i 1,2,, n
设微分方程组有 n 个首次积分
1(t, x1, x2 ,, xn ) c1,,n(t, x1, x2 ,, xn ) cn
如果在某区域内它们的Jacobi行列式
1
x1
1
x2
1
xn
D(1,,n )
D(x1,, xn )
经适当组合化为一个可积分的微分方程. 这个方程的未知函数可能是方程组中
几个未知函数组合形式. 积分可以得到未知函数组合形式的解, 该方程为一个原方程组的首次积分.
2021-5-10
5
例 4 求解方程组 dx y, dy x
dt
dt
解 将两个方程相加得 d (x y) x y
dt
以 x y 作为一个未知函数,对上式积分得
2021-5-10
13
小结:寻找首次积分的方法(技巧性强)
为了求得首次积分,通常把如下方程组
xi' fi (t, x1,, xn ) i 1,2,, n
写成对称形式 d x 1 = d x 2 = ... = d x n = d t
f1
f2
fn
1
方法1 (积分因子法)利用比例性质化分母为零,分子 为某一函数的全微分形式。(教材P350)
2u x 2
x2
2u y 2
1
于是偏微分方程 u x
2u xy
3u y3
f
(x, y)便可简单
记为L[u] f 或Lu f .
算子L若满足:L[au bv] aL[u] bL[v] 其中,a,b为常数;u, v为函数,则称L为线性算子。
偏微分方程及其求解实例ppt课件
(hn1-2.*h(k,n)+h(k,n-1))./dr.^2);
end plot(r(3:n)./ra,p(k,3:n).*theta.*2./rb)
h hi1 hi1 r i 2r
2h hi1 2hi hi1
r 2
r 2
i
P
1 rb 4
1
r
h r
2h r 2
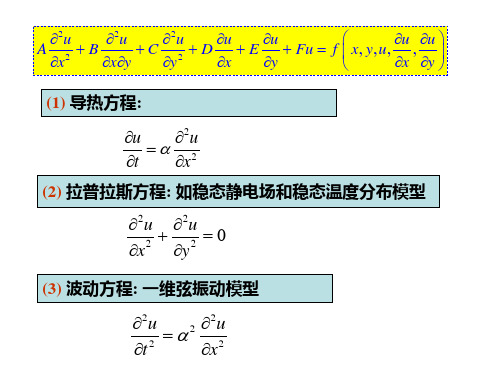
偏微分方程的求解实例2:
2u A x2
2u B
xy
C
2u y 2
D u x
E u y
Fu
f
x,
y,u,
u x
,
u y
(1) 导热方程:
u 2u
t x2 (2) 拉普拉斯方程: 如稳态静电场和稳态温度分布模型
2u 2u 0
x2 y2
(3) 波动方程: 一维弦振动模型
2u 2 2u
t 2
x2
偏微分方程的边界条件
function PDE1Dd_CrankNicolson % 使用Crank-Nicolson有限差分方法求解一维动态传
热模型
c1 = 100; c2 = 0; a = 10; b = 8; alpha = 2; n = 6; m = 8; U = CrankNicolson(@ic,c1,c2,a,b,alpha,n,m)
h t 3 9c
9c
h3 h33
4h r 4
3
h5 4h4
6h3 4h2 r 4
h1
h t
n
V
r i 2r
2h hi1 2hi hi1
r 2
r 2
i
3h r 3
hi2
2hi1 2hi1 2r 3
计算机应用基础偏微分方程求解PPT课件

6.2 二阶偏微分方程的求解
二 抛物线型偏微分方程
第16页/共43页
6.2 二阶偏微分方程的求解
parabolic函数用于求解抛物型偏微分方程的解,调用格 式如下:
u1=parabolic(u0,tlist,b,p,e,t,c,a,f,d) b: 边界条件 u0: 初始条件 tlist;时间列表 u1:对应于tlist的解向量 p,e,t :网格数据
• 启动偏微分方程求解界面
– 在 MATLAB 下键入 pdetool
• 该界面分为四个部分
– 菜单系统 – 工具栏 – 集合编辑 – 求解区域
第20页/共43页
6.3 偏微分方程求解工具箱
菜单栏
工具栏
第21页/共43页
6.3 偏微分方程求解工具箱
第22页/共43页
5.3 偏微分方程求解工具箱
第9页/共43页
6.1 偏微分方程组求解
边界条件程序”c7mbc.m” function [pa, qa, pb, qb]=c7mpbc(xa, ua, xb, ub, t) pa=[0; ua(2)]; qa=[1; 0]; pb=[ub(1)-1; 0]; qb=[0; 1];
function u0=c7mpic(x) u0=[1; 0];
进入反应器,相当于总质量速率为G=2500kg.h-1.m2。反应管
外用速率为F 130kg h-1烟道气与反应混合物
逆流加热反应管,烟道气出口温度为620 C。其
它数据:催化剂的堆积密度=1440kg / m3,操作
压力P 1.2bar,乙苯的反应热H=140000kJ / m ol,
床层有效导热系数e 0.45w.m1.k 1,有效扩散系数
偏微分方程初步介绍公开课获奖课件百校联赛一等奖课件

0, 0
第三边值问题(Robin)
经典旳定解问题举例
热传导方程旳初、边值问题
u t
a2
2u x 2
f (x, t),
t 0,0 x L
u(x, t) (x)
t 0
u( x, t) x0
g (t), u(x, t) xL
h(t)
何为适定性?
存在性 唯一性 连续依赖性(稳定性)
自变量 未知函数
F (x, u,
u x1
,,
u xn
,
2u x12
,)
0
偏微分方程旳一般形式
某些概念
PDE旳阶 古典解
PDE旳 解
广义解
线性PDE
非线性PDE
是指这么一种函数,它本身以及它旳偏导 数在所考虑旳区域上连续,同步用满足方 程。
半线性PDE 拟线性PDE 完全非线性PDE
线性PDE: PDE中对所含未知函数及其各阶导数旳全体都是线 性旳。 线性PDE中全部具同一最高阶数旳偏导数构成旳 部分,称为线性方程旳主部。
r x2 y2
6.
u t
6u
u x
3u x3
0
KDV方程
特解都不易找到
7. ut uux eu
拟线性PDE
8.
v x v xx
v
2 y
v
yy
v2
拟线性PDE
9. a( x, y)(vxx vyy ) ev (vx vy ) 半线性PDE
10. ut ux sin u
11. ut 2 ux 2 u 2
a22
y
y
a11 x
a22
y
a11 x
a22
《偏微分方程的建立》课件

根据问题的性质和已知条件,通过数学推导和逻辑推理建立偏微分方程。
求解方程
根据建立的偏微分方程,选择适当的数学方法和计算工具进行求解。
验证解的正确性
通过对比实际数据或实验结果,验证所求偏微分方程的解是否符合实际情况。
描述物理现象的偏微分方程在力学、电磁学、光学等领域有广泛应用。
物理学
偏微分方程在金融领域的应用主要涉及资产定价和风险管理等方面。
工程问题
描述生理过程、药物动力学等。
生物医学问题
04
CHAPTER
偏微分方程的实际应用案例
总结词
描述人口随时间变化的规律
详细描述
通过偏微分方程建立人口动态模型,考虑出生率、死亡率以及迁移率等因素对人口数量的影响,预测未来人口数量变化趋势。
总结词
模拟热量在物体中的传递过程
详细描述
利用偏微分方程建立热传导模型,描述热量在材料中的扩散过程,常用于材料科学、能源工程等领域。
金融学
在机械工程、航空航天、电子工程等领域,偏微分方程被用来描述各种物理现象和工程问题。
工程学
在生态学、生理学和流行病学等领域,偏微分方程被用来描述种群动态和疾病传播等现象。
生物学Biblioteka 010302
04
03
CHAPTER
偏微分方程的求解方法
方程中的未知函数及其导数都是一次幂或常数。
线性偏微分方程
方程中的未知函数及其导数是二次幂或更高次幂。
THANKS
感谢您的观看。
VS
模拟流体运动规律和特性
详细描述
利用偏微分方程建立流体动力学模型,研究流体运动的速度场、压力场、温度场等特性,广泛应用于航空航天、船舶、能源等领域。
总结词
求解方程
根据建立的偏微分方程,选择适当的数学方法和计算工具进行求解。
验证解的正确性
通过对比实际数据或实验结果,验证所求偏微分方程的解是否符合实际情况。
描述物理现象的偏微分方程在力学、电磁学、光学等领域有广泛应用。
物理学
偏微分方程在金融领域的应用主要涉及资产定价和风险管理等方面。
工程问题
描述生理过程、药物动力学等。
生物医学问题
04
CHAPTER
偏微分方程的实际应用案例
总结词
描述人口随时间变化的规律
详细描述
通过偏微分方程建立人口动态模型,考虑出生率、死亡率以及迁移率等因素对人口数量的影响,预测未来人口数量变化趋势。
总结词
模拟热量在物体中的传递过程
详细描述
利用偏微分方程建立热传导模型,描述热量在材料中的扩散过程,常用于材料科学、能源工程等领域。
金融学
在机械工程、航空航天、电子工程等领域,偏微分方程被用来描述各种物理现象和工程问题。
工程学
在生态学、生理学和流行病学等领域,偏微分方程被用来描述种群动态和疾病传播等现象。
生物学Biblioteka 010302
04
03
CHAPTER
偏微分方程的求解方法
方程中的未知函数及其导数都是一次幂或常数。
线性偏微分方程
方程中的未知函数及其导数是二次幂或更高次幂。
THANKS
感谢您的观看。
VS
模拟流体运动规律和特性
详细描述
利用偏微分方程建立流体动力学模型,研究流体运动的速度场、压力场、温度场等特性,广泛应用于航空航天、船舶、能源等领域。
总结词
最新偏微分方程数值解课件ppt

t
u
u u n
n
i , j,k 1
i , j ,k
z t n t ,x i x ,y j y ,z k z
x
Email: Jansweili@ Phone: 029—85583997
上一页
下一页
回目录
休 息
5.2 离散化公式
对于二阶偏导,我们可以通过对泰勒展开式处理技术得到下面离散化 计算公式:
u
un i 1 , j,k
un i , j ,k
x t n t ,x i x ,y j y ,z k z
x
u
un i , j 1 ,k
un i , j ,k
y
y
t n t ,x i x , y j y ,z k z
u
uin , j,1kuin ,j,k
tt(n1)t,xix,yjy,zkz
下一页
回目录
休 息
5.2 离散化公式推导
将uk+1在uk处按二阶泰勒式展开:
u k 1u kh u x kh 22 ! 2 x u 2 kO (h 3)
将uk-1在uk处按二阶泰勒式展开:
u k 1u kh u x kh 22 ! 2 x u 2 kO (h 3)
二式相加得:
x2u2 uk1
在化工或化学动态模拟方程中,常常有一个自变量是时间, 其它的自变量为空间位置。如果只考虑一维空间,则只有 两个自变量;如果考虑两维空间,则有3个自变量。 许多 化工过程均是通过对偏微分方程的求解进行工艺参数的确 定或数值模拟。
Email: Jansweili@ Phone: 029—85583997
散化,补充方程,启动递推运算
Step4 数值解计算:求解离散系统问题
偏微分方程课件 云南财经大学

1.1.5. 非线性偏微分方程 我们把不是线性偏微分方程的偏微分方程统称为非线性偏 微分方程。在非线性偏微分方程中, 如果关于未知函数的所有 最高阶偏导数都是线性的, 则称它为拟线性偏微分方程。
二阶拟线性偏微分方程 二阶拟线性偏微分方程 三阶拟线性偏微分方程
在拟线性偏微分方程中, 由最高阶偏导数所组成的那一部 分, 称为方程的主部; 若主部内的系数都是常数或是自变量的 已知函数, 这时方程被称为是半线性的。
如果给定一个函数 u (x) , 将它及它对自变量的各阶偏导
数代入方程(1.1.1), 能使(1.1.1)成为恒等式, 则称函数是偏微分方 程(1.1.1)的解。
我们知道, 一个常微分方程如果有解, 就必有无穷多个解, 其表现形式是依赖于一个或几个任意常数的通解. 于是自然会 想到偏微分方程的通解也会含有任意元素.
它被称为三维Laplace方程。
利用Laplace算子
2 x2
2 y2
2 z2
,三维Laplace方程写成
u 0
对于函数 u u(x1, x2, , xn ,t) 的n维Laplace方程,利用
Laplace算子
2 x12
2 x22
2 xn2
则偏微分方程的一般形式为
实自变量 未知函数
5
机动 目录 上页 下页 返回 结束
《偏微分方程》第一章 绪论 第6页
其中是F自变量x,未知函数u及u的有限多个偏导数的已知函数. 例如关系式
等都是偏微分方程.
6
机动 目录 上页 下页 返回 结束
《偏微分方程》第一章 绪论 第7页
1.1.2. 偏微分方程的解
m
二阶拟线性偏微分方程 二阶拟线性偏微分方程 三阶拟线性偏微分方程
在拟线性偏微分方程中, 由最高阶偏导数所组成的那一部 分, 称为方程的主部; 若主部内的系数都是常数或是自变量的 已知函数, 这时方程被称为是半线性的。
如果给定一个函数 u (x) , 将它及它对自变量的各阶偏导
数代入方程(1.1.1), 能使(1.1.1)成为恒等式, 则称函数是偏微分方 程(1.1.1)的解。
我们知道, 一个常微分方程如果有解, 就必有无穷多个解, 其表现形式是依赖于一个或几个任意常数的通解. 于是自然会 想到偏微分方程的通解也会含有任意元素.
它被称为三维Laplace方程。
利用Laplace算子
2 x2
2 y2
2 z2
,三维Laplace方程写成
u 0
对于函数 u u(x1, x2, , xn ,t) 的n维Laplace方程,利用
Laplace算子
2 x12
2 x22
2 xn2
则偏微分方程的一般形式为
实自变量 未知函数
5
机动 目录 上页 下页 返回 结束
《偏微分方程》第一章 绪论 第6页
其中是F自变量x,未知函数u及u的有限多个偏导数的已知函数. 例如关系式
等都是偏微分方程.
6
机动 目录 上页 下页 返回 结束
《偏微分方程》第一章 绪论 第7页
1.1.2. 偏微分方程的解
m
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
• 在局部坐标意义下我们可以更加直观的从
几何意义上分析其处理效果。
• 设 ξ 代表图像在某像素处的梯度方向,η
代表与梯度垂直的方向,那么上述扩散方
程可以在由 ξ 和 η 张成的局部坐标系下
表示为:
• 对于PM扩散模型,在图像的平坦区域,
C1(u) C2 (u) 进行各项同性扩散;
• 在图像的边界或纹理等梯度比较大的像素
• 最后,使用偏微分方程的突出优点是可以 使图像处理和分析的速度、准确性和稳定 性都有很大提高。PDE能获得较好的图象 处理效果,而且算法解的存在性,唯一性 与稳定性都可以在PDE独特的分析理论框 架内得到证明。
四、偏微分方程去噪问题的研究
• 基于PDE的图像处理方法在图像降噪领域 得到了广泛的重视,因为它在平滑噪声的 同时,可以使得图像的细节,如边缘和纹 理得到保护。
• 德国科学家Weickert通过在扩散项中引入扩 散张量的概念提出了各向异性的一致增强 扩散方程。
他提出如下的扩散系数:
其中,k>0用于判断特征,相应的扩散方 程为:
• 在此基础上,Perona和Malik提出了他们著 名的P-M方法:
• 其中
或
• 区域的内部,即图像的梯度模 u 比较小时
,此时函数c 1,扩散方程近似于热扩散
过程,具有各向同性的特点。
• 在图像的边界或细节处,即梯度模 u 较大 的像素处,扩散系数c(s) -> 0,从而边界特 征被保持。
• 它是一个热传导方程的解。
• 它可以视为一个各向同性均匀的热扩散过 程。
• 一个自然的想法就是考虑利用图像结构的 先验信息,减少在边缘处的扩散以在去噪 的同时更好地保持边缘。
• 一个简单的思路是将梯度算子作为边缘检 测算子,来控制扩散的速度。
• Perona和Malik就是沿着这个方向,提出了 各向异性的扩散方法,此后这个方法得到 了广泛的关注。针对扩散模型和其数值求 解方面都有很大的发展。
• Perona和Malik提出各向异性扩散方程在这 个领域最具有影响力。他们提出用一个保 持边缘的有选择性的扩散来替换Gaussian 扩散。他们的工作引发了很多理论和实际 问题的研究。
• Osher和他的研究小组提出了几何制约的偏 微分方程,其中最著名的是曲率流。
• 曲率流是“纯粹的”各向异性扩散模型, 它使图像灰度值的扩散只发生在图像梯度 的正交方向上,在保持图像轮廓精确位置 和清晰的同时沿轮廓进行平滑去噪。
• 另一方面,当图象表示为连续信号,PDE 可视为具有微小子邻域局部滤波器的迭代 ,这种在PDE框架内的解释允许将现有的 滤波方法进行合并与分类,更加容易理解 其对应的物理意义,并可直观地设计出新 的滤波方法。进一步,PDE使得图象处理 的合成非常自然。
例如给定两个不同的图象处理方案: 可以轻易合成为:
偏微分方程起源于热传导方程的初始值问题 。设初始灰度图像为u(x, y, 0) , u(x, y, t)为在时 间t时的平滑图像。
则图像的热传导平滑方程为:
各向同性扩散(热扩散模型)
• 式中△u(x, y, t)为图像的拉普拉斯算子。方 程的解为u(x, y, t) = Gσ* u(x, y, 0) ,即不同尺 度的高斯滤波器与初始图像的卷积。其中
• 他们的贡献在很大程度上构成了偏微分方 程图像处理理论的基础。在他们的研究工 作中,图像的多尺度表示是通过高斯平滑 来获得的,这等价于利用经典的热传导方 程来演化图像得到一个各向同性扩散流。
• 在80年代末,Hummel提出热传导方程并不 是唯一可以产生尺度空间的抛物方程,并 提出构成尺度空间的准则:只要满足最大原 则的演化方程就可以定义一个尺度空间。
基于偏微分方程(PDE)的图 像去噪
2011-09-06
目录
• 一、偏微分方程图像处理发展过程 • 二、偏微分方程图像处理数学基础 • 三、偏微分方程图像处理的优缺点及应用
结构 • 四、偏微分方程去噪问题的研究
• 4.1 各向同性扩散(热扩散模型) • 4.2 P-M非线性扩散
• 五、偏微分方程其他方面的简略介绍
一、偏微分方程图像处理发展过 程
在过去几十年,计算机可视化和图像分析 领域中以偏微分方程为基础的模型在图像 处理研究领域占据着重要地位。
• 使用偏微分方程处理图像的思想可以追溯 到Gabor和Jain。
• 但是这种方法真正建立起来是Koenderind 和Witkin的研究工作开始的,他们引入了尺 度空间(Scale Space)的概念,尺度空间把 一组图像同时在多个尺度上表述。
目录
优点
使用偏微分方程进行图像处理有很多优点。 • 使用偏微分方程可以用广义上连续的二维
函数来对图像进行建模,从而对图像进行 求导求积分等操作,这就把图像处理问题 规范化,使问题的描述在形式上变得简单 。
• PDE给出了连续域上图象的分析模型。模 型与数字图象的网格(对应于图象像素)大小 无关,当假定网格网孔大小趋于零时,离 散滤波器在PDE中可理解为连续微分算子 的近似,从而使得网格的划分与局部非线 性滤波分析易于实现,简化了图象的分析 体系。
偏微分方程是从运动的观点来处理图像的,对 于图像去噪的过程,我们可以用偏微分方程予 以表达。用uo:R2--->R表示一幅灰度图像,灰 度值为u(x,y)。引入时间因子t,则对图像的处 理以偏微分方程表示可写为:
• 其中u(x, y; t) : {0, T} R2 R为变化过程中 的图像,F:R2->R表示某中给定的算法
• 只有在空间定义域和灰度值上都离散化了 的图象才能被计算机处理,这种离散化图 象称为数字图象,空间离散化称为空间采 样,灰度离散化称为灰度量化。
目录
• 离散图象的模型用u: xΩ [0,255]表示,
这里x=(x,y)是离散的,[0, 255]表量化的 256个灰度级。
• 尽管图象在计算机中以上述离散形式存储 ,但由于在空间采样与灰度量化上这种离 散化都足够精细,从而可以用连续(或分段 连续)的数学函数近似。
• 2002年Guy Gilboa等人提出选取不定的扩 散张量,打破了以往扩散模型非负的要求 ,通过改变其符号实现自适应的FAB(正倒 向)扩散。
• 2004年Guy Gilboa又提出了复扩散模型, 把扩散模型引入到复域上
• 现在基于偏微分方程的图像去噪正向着更 复杂的方向发展,与数学形态学、小波变 换等相结合的复合去噪方法成为一个热门 研究方向。
改进
• Catte 等通过对梯度模进行正则化实现了稳 定的Pernoa-Malik模型。
• Alvarez, dons等将平均曲率流引入到PM模 型中。
• 北京大学的石青云教授和微软亚洲研究院 的林宙辰博士(as)提出了一种能去噪和保持 真实感的各向异性扩散方程,它还能保持 图像中有意义的较强的尖峰和窄边缘。
• Osher和Rudin关于激波的研究以及关于TV 模型的研究工作更突出了偏微分方程在图 像处理中的重要性,这些方法成功之处在 于将图像视为由跳跃边缘连接而成的分片 光滑函数(曲面),从而与某种偏微分方程的 分片光滑解联系起来。
二、偏微分方程图像处理数学基 础
• 在基于偏微分方程的图象处理中,对图象 模型有连续与可微的要求,需要建立图象 的连续模型。
• 通常依赖u 于图像及其图像空间上一、二阶 导数,n =0为绝热条件,保证扩散仅在图 像边界内进行。
• 这是一个以uo为初始条件的发展方程,偏 微分方程的解试u(x, y, t)即给出了迭代t次时 的图像。
• 在得到满意的图像时即停止迭代,这就是偏 微分方程表达的图像处理过程。
各向同性扩散(热扩散模型)
• 国防科技大学的谢美华等从偏微分方程去 噪模型出发 ,论述了噪声抑制的原理。
• 考虑到传统的各向异性扩散模型无法正确 的对边缘定向,提出了一种基于边缘定向 增强的各向异性扩散去噪方法,首先利用 基于非线性光滑算子的边缘定向算子对边 缘定向然后利用边界信息确定扩散张量, 从而达到既保护边界又具有良好的去噪效 果。
• 如果图像存在噪声,例如椒盐噪声,则在 噪声点(x,y)约处,图像的梯度 u(x, y,t) 可能非常大,此时扩散系数c(x, y,t)非常小 ,从而将这些噪声点保留下来,降低了去 噪性能。
• 上述扩散方程是病态的,同一个初始条件 可以产生多个解.实际上,为了保证解的存 在性和唯一性,必须要求C(s)为非降函数. 如果此条件不满足,则此过程不稳定。
目录
• 源于约束最优化、量最小化和变分方法的 PDE方法的基本思想是将所研究问题归结 为一个泛函极小问题;
• 然后应用变分方法导出一个或一组偏微分 方程;
• 最后用数值计算方法求解此偏微分方程, 得到所要的数值解,这个数值解就是一幅 恢复图像。
• 从高斯滤波引入的,理论研究和数值运算 均表明,大部分线性滤波算子的极限都是 一个微分算子。
• 定位特性:在不同的尺度下,图像特征的空 间位置变化情况为定位特性。热方程在大 尺度上所保留下来的图像特征,其空间位 置会展宽且发生漂移。
P-M非线性扩散
• 高斯热传导滤波造成边缘模糊主要是因为 热扩散方程在图像各个位置上的扩散程度 是一致的,并不区分是噪声还是图像特征 。
• Charbonnier 提出如果利用c( u0 )。作为特 征检测算子,在 c( u0 )较大的区域减少扩 散就可以使特征得到更多的保护。
这样若算子F1和F2分别为光滑与边缘保护 算子,则新的合成方案将同时具有去噪与 保护边缘的图象恢复效果。
• 在计算方面,可以很好的利用现在已有的 一些非常完备的数值分析和偏微分方程计 算方法来进行运算,为PDE的数值计算给予 了极大的帮助,它能从已有的有关数值分 析和计算偏微分方程的许多文献中大大获 益。
处,C1(u) C2 (u) 此时ቤተ መጻሕፍቲ ባይዱ像沿着与几乎与
