数学改编题
小学数学试题改编及设计方案

小学数学试题改编及设计方案引言在小学数学教学中,试题是提供给学生练习和巩固知识的重要资源。
然而,传统的试题往往缺乏趣味性和创新性,难以激发学生的学习兴趣和思维能力。
为了提高小学数学教学的效果,我们需要改编和设计创新的试题,以帮助学生更好地理解和掌握数学知识。
本文将介绍一些小学数学试题改编和设计的方案,以及其应用和效果。
改编试题的意义改编试题是对传统试题进行创新和改进,以满足学生不同的学习需求和认知水平。
通过改编试题,我们可以提供更多趣味性和挑战性的问题,激发学生的学习兴趣和思维能力。
同时,改编试题还可以帮助学生理解数学知识的应用场景,从而提高他们解决实际问题的能力。
改编试题的方法改编试题的方法有多种,下面将介绍几种常用的方法。
增加情境元素在传统的试题中,可以增加一些情境元素,使问题更具生活化和趣味性。
例如,在解决加法问题时,可以改为小明买了几个苹果,小红又买了几个苹果,他们一共买了多少个苹果?这样的问题使学生更容易理解和解决。
提供多样化的问题形式传统的试题往往只有一种形式,学生很容易记住答案的计算步骤,但缺乏理解。
改编试题时,可以提供多样化的问题形式,让学生从不同的角度思考问题。
例如,在解决乘法问题时,可以以表格或图形的形式呈现问题,让学生通过图示来理解和解决问题。
设置拓展问题在传统试题的基础上,可以增加一些拓展问题,提高问题的难度和挑战性。
这些问题可能需要学生运用多个数学概念和技巧来解决,这样可以培养学生的综合运用能力和创造性思维。
设计方案的实施与效果在设计方案实施的过程中,需要注意以下几点:理解学生的认知水平在设计试题时,需要充分理解学生的认知水平和学习需求。
试题的难度应该适中,既能够挑战学生,又能够让他们有一定的成功体验。
同时,还需要结合学生的实际情况和兴趣爱好来设计试题,增加学生的参与度和积极性。
提供解题思路和方法在试题的设计中,应该提供一些解题思路和方法,帮助学生理解和解决问题。
可以通过设置引导性问题、提供解题步骤和提示等方式来引导学生思考和解题。
新编【人教A版】高中数学:必修2课本例题习题改编(含答案)
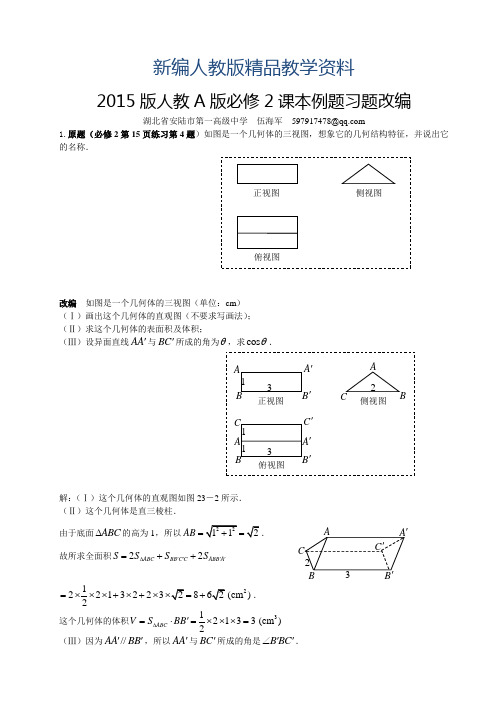
新编人教版精品教学资料2015版人教A 版必修2课本例题习题改编湖北省安陆市第一高级中学 伍海军 ****************1.原题(必修2第15页练习第4题)如图是一个几何体的三视图,想象它的几何结构特征,并说出它的名称.改编 如图是一个几何体的三视图(单位:cm ) (Ⅰ)画出这个几何体的直观图(不要求写画法); (Ⅱ)求这个几何体的表面积及体积;(Ⅲ)设异面直线AA '与BC '所成的角为θ,求cos θ.解:(Ⅰ)这个几何体的直观图如图23-2所示. (Ⅱ)这个几何体是直三棱柱.由于底面ABC ∆的高为1,所以AB ==. 故所求全面积22ABC BB C C ABB A S S S S ''''∆=++1221322382=⨯⨯⨯+⨯+⨯=+2(cm ).这个几何体的体积121332ABC V S BB ∆'=⋅=⨯⨯⨯=3(cm )(Ⅲ)因为//AA BB '',所以AA '与BC '所成的角是B BC ''∠.O OO 'O '22OO在Rt BB C''∆中,BC '==cos BB BC θ'===' 2.原题(必修2第28页例3)如图,已知几何 体的三视图,用斜二测画法画出它的直观图. 改编1 如图,已知几何体的三视图(单位:cm ). (Ⅰ)画出它的直观图(不要求写画法); (Ⅱ)求这个几何体的表面积和体积. 解:(Ⅰ)这个几何体的直观图如图所示. (Ⅱ)这个几何体是一个简单组合体,它的下部是 一个圆柱(底面半径为1cm ,高为2cm ),它的上部 是一个圆锥(底面半径为1cm ,母线长为2cm ,高为).所以所求表面积21212127S ππππ=⨯+⨯⨯+⨯⨯=2(cm ),所求体积22112123V πππ=⨯⨯+⨯⨯=3(cm ).3.原题(必修2第30页习题1.3B 组第三题)分别以一个直角三角形的斜边,两直角边所在直线为轴,其余各边旋转一周形成的曲面围成三个几何体,画出它们的三视图和直观图,并探讨它们体积之间的关系。
小学数学题目改编题及意图

小学数学题目改编题及意图一、题目改编1. 题目原始版本:小明有3只红色的气球,小红有4只蓝色的气球。
请问他们一共有多少只气球?2. 改编后的题目:小明有一些红色的气球,小红有一些蓝色的气球。
如果他们一共有7只气球,那么小明有几只红色的气球?二、意图解析1. 题目原始版本意图:考察学生的简单加法运算能力,要求学生将小明和小红拥有的气球数量相加。
2. 改编后的题目意图:考察学生的解方程能力,要求学生通过解一个简单的一元一次方程,求出小明拥有的红色气球数量。
三、意图对比及优势原始版本的题目主要是为了培养学生的基础加法算术能力,题干中提供了具体的气球数量,要求学生直接相加得到答案。
而改编后的题目则更注重培养学生的解方程思维能力,通过给出总气球数量,要求学生推导得到小明红色气球的数量。
改编后的题目更具挑战性,需要学生运用已学的方程求解方法来解决问题。
同时,此题也激发了学生解决实际问题的能力,让学生在数学中体验到实用性和乐趣性。
四、题目应用场景改编后的题目可以应用于小学数学教育中,作为培养学生应用数学知识解决实际问题的案例。
此题不仅仅是简单的纯数学计算,更强调对数学概念的理解和运用。
让学生通过解方程的方法,掌握并运用数学知识解决日常生活中的实际问题。
在教学中,可以提供一些类似改编题目的训练,帮助学生提高解决实际问题的能力,并培养学生的数学思维和创新能力。
五、总结通过对小学数学题目的改编,可以提升学生的数学解题能力,引导学生从简单的计算中逐渐转向解方程和解决实际问题的能力。
改编题目要注意题目的合理性和可解性,要保证学生在已掌握的知识范围内能够解答出来。
同时,在改编题目的过程中,也可以适当增加一些创新和趣味性,激发学生对数学的兴趣和好奇心。
通过改编题目,可以丰富教学内容,提高课堂教学的趣味性和实用性,培养学生的数学思维和解决实际问题的能力,更好地发展学生的综合素质。
如何进行原创或改编试题(数学)

如何进行原创或改编试题(数学)如何进行原创或改编试题(数学)试题是教育教学过程中起到关键作用的一种教学工具。
合理设计试题不仅能够有效评估学生的学习情况,还能激发学生的学习兴趣和创造力。
本文将就如何进行原创或改编数学试题进行探讨。
一、确定试题类型在进行试题设计之前,首先需要明确试题的类型。
数学试题主要包括选择题、填空题、计算题和解答题等。
根据教学目标和学生的学习需求,选择合适的试题类型。
二、把握试题难度试题难度的确定与学生的能力水平息息相关。
设计试题时,要综合考虑学生的认知水平、解题能力和学科的知识体系。
试题的难度应该适当挑战学生,但也不能过于超出他们的能力范围。
三、运用创意设计试题1. 创新思维题鼓励学生运用创新思维方式进行问题解决。
可以设计一些开放性问题,鼓励学生自由发挥,充分展示他们的思维能力和创造力。
2. 情境问题设计一些与现实生活相关的情境问题,让学生将数学知识应用于实际生活中。
这样的题目能够增强学生的兴趣,并培养他们将数学知识与实际问题结合的能力。
3. 多元化题型除了传统的选择题、填空题、计算题等,还可以设计一些多元化的题型,如拼图题、实物拼装题、证明题等。
这样的题目不仅能锻炼学生的动手操作能力,还能激发他们的思考和创造力。
四、合理安排试题顺序试题的顺序安排也很重要。
通常可以从易到难、由浅入深的方式进行。
这样能够逐步引导学生掌握知识,在解题过程中逐步提高难度,有助于学生的思维发展。
五、充分利用资源在进行试题设计时,可以充分利用各种教学资源。
可以参考教材、习题集以及相关的学术论文,借鉴已有的试题和解题思路,结合自身的教学实践进行新的改编和创新。
六、反思和修改完成试题设计后,需要进行反思和修改。
在教学过程中应不断重视学生对试题的反馈。
根据学生的理解情况和解题过程中可能出现的困惑,及时对试题进行修正和调整,确保试题的质量和有效性。
七、尊重知识产权在进行试题设计时,应尊重知识产权。
使用他人的试题或参考资料时,应注明出处,并征得相关权利人的许可。
重要题型改编练习(试题)-二年级上册数学人教版

二年级上册重要题型改编练习1.水果店原来的芒果和火龙果同样多。
又运回了32箱芒果和一些火龙果,现在水果店里的芒果比火龙果多7箱,你知道水果店又运回了多少箱火龙果吗?2.买玩具。
(1)依依拿50元钱去买了一个布娃娃和一个计数器,找回了8元,这个布娃娃多少钱?(2)妈妈给了淘淘100元钱,他想买两件不同的玩具而且要找回的钱最少,他可以买哪两件不同的玩具?3.现在有多少颗松果?4.淘淘和壮壮进行百米游泳比赛,这时淘淘游了多少米?5.实验小学开展“我是东坡阅读小学士”活动,计划将学校图书室的76本书奖励给二年级的“东坡阅读小学士”们,每人奖励一本书。
还剩下多少本书? (用两种方法解答)6.地铁上原来有82名乘客,到了某站后,先下去48名乘客,又上来56名乘客,地铁上现在还有多少名乘客?7.这一队共有多少人?8.根据给出的信息和算式提出相应的问题。
( 1 ) 提问:( 2 ) 提问:算式:3 2 - 1 1 = 2 1 ( 下) 算式:3 2 + 8 + 3 2 = 7 2 ( 下)9.一本《动物世界》有100页,龙一鸣前两天一共看了多少页?如果第三天看30页,他第三天能看完这本书吗?10.黄老师1 1月底还剩多少元话费?如果再充5 0元,手机里有多少元话费?11.原来体育器材室里的乒乓球拍比羽毛球拍多12副,这学期新购进了25副乒乓球拍和42副羽毛球拍。
现在体育器材室里的乒乓球拍多还是羽毛球拍多?多多少副?12.你能用乘法算式表示出这些花的总盆数吗?试一试。
13.这首诗一共有多少个汉字?14.一列小火车可坐5人。
15.1只青蛙4条腿,荷叶上有1只大青蛙和4只小青蛙,这些青蛙一共有多少条腿?。
数学试题改编的几种策略与方法初探

数学试题改编的几种策略与方法初探在数学试题的改编上有多种方法,我个人认为大致有三种:纵向改编、逆向改编、横向改编。
纵向改编以一道题为主线实行深挖、拓展、强化等的改编,逆向改编是把原命题实行逆向思维实行改编,横向改编是一道题的思想与多道题思想与方法相综合实行改编。
下面我就几道常见的几何题从这几个方面上实行改编谈一些体会和想法1.纵向改编:原题:等边△ABC,点D在BC边上,连接AD,把△ABD绕点A逆时针旋转60°,画出旋转后的图形。
改编思路:等边△ABC,点D在三角形ABC的内部,把△ABD绕点A逆时针旋转60°得到△ACD'.连接DD',若点B在直线DD'上,DD'交AC于点E,判断AD与CD'的位置关系当点D’在直线BD上时,如图:变式一:如图:等边△ABC的边AC上一点D,连接BD,点E、点F在直线BD上,且∠AED=∠ABC,CF∥AE,求线段CF、AE、BF的数量关系答案:CF+AE=BF解答思路:旋转全等,证明△ACE≌△ABE CF=BE AE=EF CF+AE=BF 如图:改编思路:把等边三角形改为夹角为60度,两边比为1:2的三角形(369三角形)变式二:如图:△ABC的边AC上一点D,连接BD,点E、点F在直线BD上,且∠AED=∠ABC,CF∥AE∠ABC=60°,∠ACB=30°,求线段CF、AE、BF的数量关系答案:CF+2AE=BF证明思路:旋转相似证明△BCP∽△ABE 等边三角形PCF CF=PC=2BE 2AE=BP CF+2AE=BF变式三:如图:△ABC的边AC上一点D,连接BD,点E、点F在直线BD上,且∠AED=∠ABC,CF∥AE若AB:BC=1:k,∠ABC=60°,求线段CF、AE、BF的数量关系答案:kAE+CF=BF证明思路:旋转相似证明△BCQ∽△ABE 等边三角形PCF CF=QC=kBE kAE=BQ CF+kAE=BF改编思路:把三角形在实行一般化,如下:变式四:如图:△ABC的边AC上一点D,连接BD,点E、点F在直线BD上,且∠AED=∠ABC,CF∥AE若AB:BC=1:k,∠ABC=α°,求线段CF、AE、BF的数量关系(用含α,k的代数式表示)答案: kAE+2cos α•CF=BF证明思路:旋转相似 证明 △BCQ ∽△ABE 等腰三角形PCF CF=QC=2cos αkBE kAE=BQ kAE+2cos α•CF=BF改编思路:把三角形在实行一般化,把∠F 再实行特殊化,如下:变式五:如图:△ABC 的边AC 上一点D ,连接BD ,点E 、点F 在直线BD 上,且∠AED=∠ABC ,CF ⊥BF 若AB :BC=1:k,∠ABC=α°,求线段CF 、AE 、BF 的数量关系(用含α,k 的代数式表示)答案:kAE+(CF/tan α)=BF证明思路:相似 证明 △BCQ ∽△ABE Rt △PCF CF=QF tan α CQ=kBE kAE=BQkAE+(CF/tan α)=BF2.逆向改编: 原题:Rt △ABC 中,∠C =90°,AC =BC ,D 是AB 边上一点,k DBAD=,E 是在AC 边上的一个动点(与点A 、C 不重合),DF ⊥DE ,且DF 与射线BC 相交于点F . 当k=1时,求证:AB BF AE 22=+; 变式一:图2,当k=0.5时,请直接写出AE 、BF 、AB之间的数量关系:____________________.FBCAE图1FBACE这是一道典型的对角互补的图形变换问题,我们知道解决对角互补的问题常见的方法有两种,一种是作高,一种是旋转。
小学数学改编练习题

小学数学改编练习题题1:小明有一些苹果,小华给了他7个苹果,小明又捡了15个苹果来,他现在有多少个苹果?解答:设小明手里原有的苹果数量为X,则根据题意可以列出方程X + 7 + 15 = 总苹果数量。
因此,小明现在手里的苹果数量为 X + 7 +15 个。
题2:一个数减去20,再加上35,结果是55,这个数是多少?解答:设要求的数为 Y,则根据题意可以列出方程 Y - 20 + 35 = 55。
经过整理,得到 Y = 40。
所以这个数为 40。
题3:小华有20元,小明的钱是小华的一半,小明还有多少钱?解答:设小明的钱为 Z,则根据题意可以列出方程 20 = Z + Z/2。
求解方程,得到 Z = 40。
所以小明还有 40 元。
题4:一个数加上19,再减去35,结果是-5,这个数是多少?解答:设要求的数为 W,则根据题意可以列出方程 W + 19 - 35 = -5。
经过整理,得到 W = 21。
所以这个数为 21。
题5:一个三位数百位数是4,十位数是5,个位数是6,这个数是多少?解答:这个三位数可以表示为 4 × 100 + 5 × 10 + 6 × 1 = 400 + 50 + 6 = 456。
所以这个数为 456。
题6:一本书共有100页,小明读了其中的3/4页,他读了多少页?解答:小明读的页数可以表示为 100 × (3/4) = 300/4 = 75。
所以小明读了 75 页。
题7:小红有20根铅笔,她用了其中的3/5,她用了多少根铅笔?解答:小红用掉的铅笔数量可以表示为 20 × (3/5) = 60/5 = 12。
所以小红用了 12 根铅笔。
题8:小明一共有40个糖果,他分给小红和小华,小红得了其中的2/5,小华得了多少个糖果?解答:小华得到的糖果数量可以表示为 40 × (1 - 2/5) = 40 × (3/5) = 120/5 = 24。
初中数学题目改编

初中数学题目改编惠阳区良井中学编者:张立鹏一、原题是九年级下册(人教版)P23探究1。
原题考查目标:会运用二次函数解决实际问题,根据问题找等量关系求出函数解析式,再求出二次函数最值时的自变量的值新题:某件衣服现在的售价为每件60元,每个月可卖出300件。
市场调查放映;如调整价格,每涨价1元,每月要少卖10;每降价1元,每月可多卖出20件,已知这种衣服的进价为每件40元,当衣服的售价为x元,每月的销售量为y件,(1)写出y与x的函数关系式及x的取值范围(2)要使利润最大应该涨价还是降价?如果涨价应涨多少,降价应降多少,怎么定价?考查目标:本问题是一道较复杂的市场营销问题,培养学生分类讨论的数学思想方法,通过本问题的设计,让学生体会二次函数模型在同一个问题中的不同情况下是不同的,培养学生考虑问题的完善性,养成前面分析问题的良好习惯,提升解决问题的能力。
分析:(1)调整价格包括涨价和降价两种情况。
(2)设每件涨价x元。
则月售出商品的利润y随之变化。
我们先来确定y随x变化的函数式。
涨价x元时,每月少卖10x件,实际卖出(300-10x)件,销售额为(60+x)(300-10x)元,买进商品需付40(300-10x)元。
设每件降价X元,则每月可多卖20x件,实际卖出(300+20x)件。
销售额为(6-x)(300+20x)元,买进商品需付40(300+20x)元。
答案:解(1)当涨价时:y=300-10(x-60)=900-10x,x>60当降价时:y=20(60-x)+300=1500-20x,40≤x≤60 (3分)(2)设每件涨价x元,每月少卖10x件,实际卖出(300-10x)件。
由题意可得y =(60+x)(300-10x) -40(300-10x),即y = -10x2+100x+6000。
(0≤x≤30.)当X=5 时,y最大=6250元。
即售价为65元时,利润最大。
(2分)设每件降价x元,每月多卖20x件,实际卖出(300+20x)件,由题意可得y = ( 60-x )( 300+20x ) - 40 ( 300+20x ),即y = -20x2+100x+6000当x=2.5时,即售价为57.5元时,利润最大为6125元。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学改编题
惠阳区良井中学贺炯军
原题目出自人民教育出版社日期:2011年10月25日
1、等腰三角形题型转换
(出自人民教育出版社教材66页复习题12第14题)
如图,△ABC是等边三角形,BD是中线,延长BC至E,使CE=CD,求证:DB=DE。
考查目标:本题在学习等腰三角性质与判定的基础上进行延伸,应用到了三角形外交和等于与他不相邻的两个内角和,以及三角形内角和定理,角平分线的定义等知识。
证明:∵△ABC是等边三角形
∴三角形的内角均为60°(1分)
∵BD是中线
∴BD平分角∠CBA,则∠CBD=30°(1分)
延长BC至E,使CE=CD
在△CDE中∠DCE=120°
∴∠CDE=∠CED=30°(2分)
在△BDE中∠EBD=∠BED=30°
∴DB=DE(2分)
变式:如图,△ABC是等边三角形,D是AC上移动的一点,延长BC至E,使CE=CD。
无论D移动至何处时,连接DE所成的线段始终保持怎样的关系,请说明理由。
解:相互平行
使D点移动到D',延长BC至E’,使CE’=CD,
∵△ABC是等边三角形
∴三角形的内角均为60°(1分)
∵BD是中线
∴BD平分角∠CBA,则∠CBD=30°(1分)
延长BC至E,使CE=CD
在△CDE中∠DCE=120°
∴∠CDE=∠CED=30°(2分)
同理∠CE’D=30°
∴D'E’∥DE(2分)
考查化归与转化的数学思想方法:以原题的考查目标为基础,把等腰三角形的判定转换为平行线的判定,提高学生的观察图形能力和解题思维能力。
2、三角形全等的题型转换
(出自人民教育出版社教材26页复习题11第3题)
如图,CD=CA,∠1=∠2,EC=BC。
求证:DE=AB.
考查目标:三角形全等的性质与判定。
证明:∵∠1=∠2 ∠BCA=∠1+∠ECA ∠ECD=∠ECA+∠2
∴∠BCA=∠ECD (1分)
又∵CD=CA,EC=BC
∴△ABC≌△DEC(3分)
∴AB=DE(2分)
变式:如图1,点B是线段AD上一点,△ABC和△BDE分别是等边三角形,连接AE和CD.
(1)求证:AE=CD;
(2)如图2,点P、Q分别是AE、CD的中点,试判断△PBQ的形状,并证明.
(1)证明:∵△ABC和△BDE是等边三角形
∴AB=CB,BE=BD, ∠ABC=∠DBE=60°
∵∠ABE=∠ABC+∠CBE, ∠CBD=∠DBE+∠CBE
∴∠ABE=∠CBD(2分)
在△ABC和△BDE中
AB=CB
BE=BD
∠ABE=∠CBD
∴△ABC≌△BDE(SAS)
∴AE=CD(2分)
(2) △PBQ 是等边三角形
证明:有(1)可知△ABC ≌△BDE
∴AE=CD ,∠BAP=∠BCQ ,AB=CB
∵点P 、Q 分别是AE 、CD 的中点
∴CQ=AP (2分)
在△ABP 和△CBP 中
AB=CB
∠BAP=∠BCQ
CQ=AP
∴△ABP ≌△CBP (SAS )(3分)
∴PB=QB, ∠ABP=∠CBQ
∵∠ABC=∠ABP+∠PBC=60°
∴∠PBQ=∠PBC+∠CBQ=60°
∴△PBQ 是等边三角形(2分)
考查化归与转化的数学思想方法:结合三角形全等的性质与判定、等边三角形的性质与判定的解题方法。
考查学生的分析题目能力,解题方法。
3、等腰三角形的题型转换
(出自人民教育出版社教材56页习题12、3第1题)
等腰三角形的一个角是80°,它的另外两个角是多少度?
解:若顶角是80°
则两个底角是(180°-80°)÷2=50°
若底角是80°
则顶角是180°-80°-80°=20°(3分)
考查目标:对等腰三角形的定义以及性质的理解。
变式:已知等腰三角形的周长为20,其中一内角的余弦值是3
2 ,求这个等腰三角形的腰长.
解:如图,等腰三角形ABC 中,周长为20
①若底角的余弦值是32,则cosB=3
2 做AD 垂直于BC ,交BC 于点D
易得AB+BD=21(AB+AC+BC )=10,且AB AD =32 解可得:腰长AB=6(3分) ②若顶角的余弦值是32,则cosA=3
2 做BD 垂直于AC ,交AC 于点D
设AB=x ,则AD=3
2x ,由勾股定理可得BD=35x 在Rt △BCD 中,CD=x-
32x=31x ,BD=35x 解可得:BC=3
6x 又有AB+AC+BC=20,即2x+
36x=20 解可得x=12-26(4分)
答:腰长为6或12-26.
考查化归与转化的数学思想方法: 在正确理解等腰三角形的定义以及性质的基础上,多方便、多角度的考虑问题,发散学生的思维能力。
