西城区高一期末数学试卷及答案
北京市西城区学年高一下学期期末质量检测数学试题

X 市西城区〔南区〕202X-202X 学年下学期高一期末质量检测数学卷子本卷子总分值100分,考试时间120分钟。
一、选择题:本大题共12小题,每题3分,共36分。
1. 与角-70°终边相同的角是A. 70°B. 110°C. 250°D. 290°2. sin43°cos17°+cos43°sin17°的值为 A. 21- B. 21 C. 23 D. 23- 3. 已知向量a =)1,(x ,b =),4(x ,假设向量a 和b 方向相同,则实数x 的值是A. -2B. 2C. 0D. 58 4. 函数)3sin(π-=x y 的单调递增区间是 A. )](265,26[Z k k k ∈++-ππππ B. )](2611,265[Z k k k ∈++ππππ C. )](234,23[Z k k k ∈++ππππD. )](23,232[Z k k k ∈++-ππππ 5. 假设直线过点〔1,1〕,〔2,31+〕,则此直线的倾斜角的大小为A. 30°B. 45°C. 60°D. 90°6. 在等差数列}{n a 中,1091=+a a ,则5a 的值为A. 5B. 6C. 8D. 107. 如下图, M 是△ABC 的边AB 的中点,假设b CA a CM ==,,则CB =A. b a 2-B. b a -2C. b a 2+D. b a +28. 与直线012=+-y x 关于直线1=x 对称的直线的方程是A. 012=-+y xB. 012=-+y xC. 032=-+y xD. 032=-+y x9. 设n S 为等比数列}{n a 的前n 项和,已知23,233243-=-=a S a S ,则公比q 等于A. 3B. 4C. 5D. 610. 已知直线过点A 〔1,2〕,且原点到这条直线的距离为1,则这条直线的方程是A. 0543=+-y x 和1=xB. 0534=+-y x 和1=yC. 0543=+-y x 和1=yD. 0534=+-y x 和1=x11. 设y x ,满足约束条件⎪⎩⎪⎨⎧-≥≤≤+21y x y y x ,则y x z +=3的最大值为A. -8B. 3C. 5D. 712. 点),(y x P 是函数)25,21(sin 23)(⎥⎦⎤⎢⎣⎡-∈=x x x f π图象上的点,已知点Q 〔2,0〕,O 为坐标原点,则QP OP ⋅的取值范围为A. ]0,1[-B. ]2,1[-C. ]3,0[D. ]13,1[--二、填空题:本大题共6小题,每题3分,共18分。
2024届北京市西城区普通中学数学高一下期末考试试题含解析

2024届北京市西城区普通中学数学高一下期末考试试题考生请注意:1.答题前请将考场、试室号、座位号、考生号、姓名写在试卷密封线内,不得在试卷上作任何标记。
2.第一部分选择题每小题选出答案后,需将答案写在试卷指定的括号内,第二部分非选择题答案写在试卷题目指定的位置上。
3.考生必须保证答题卡的整洁。
考试结束后,请将本试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.圆221:1O x y +=与圆222:30O x y +--+=的位置关系是( )A .外离B .相交C .内切D .外切2.设等比数列{}n a 的前n 项和为n S ,且510315S S ==,,则20S =( ) A .255B .375C .250D .2003.若角α的终边过点(1,2)-,则sin2α=( ) A .45B .2-5C .25D .45-4.已知直线l 经过点(1,2)P -,且倾斜角为45,则直线l 的方程为( ) A .30x y --= B .10x y --= C .30x y -+=D .30x y +-=5.已知正实数x y 、满足224x y +=,则的最大值为( )A .2B .52C .3D .946.在某次测量中得到A 样本数据如下:43,50,45,55,60,若B 样本数据恰好是A 样本每个数都增加5得到,则A 、B 两样本的下列数字特征对应相同的是( ) A .众数B .中位数C .方差D .平均数7.执行如图所示的程序框图,若输出的S =88,则判断框内应填入的条件是( )A .B .C .D .8.函数cos tan y x x =⋅(302x π≤<且2x π≠)的图像是下列图像中的( ) A . B .C .D .9.已知函数()sin()0,||2f x x πωϕωϕ⎛⎫=+><⎪⎝⎭的最小正周期是π,其图象向右平移3π个单位后得到的函数为奇函数.有下列结论: ①函数()f x 的图象关于点,012π⎛⎫-⎪⎝⎭对称;②函数()f x 的图象关于直线512x π=对称;③函数()f x 在52,123ππ⎡⎤⎢⎥⎣⎦上是减函数;④函数()f x 在7,312ππ⎡⎤⎢⎥⎣⎦上的值域为1,12⎡⎤⎢⎥⎣⎦.其中正确结论的个数是( ) A .1B .2C .3D .410.某次运动会甲、乙两名射击运动员成绩如右图所示,甲、乙的平均数分别为为x 甲、x 乙,方差分别为2s 甲,2s 乙,则( )A .22x x s s >>甲乙甲乙,B .22x x s s ><甲乙甲乙,C .22x x s s 甲乙甲乙,D .22x x s s <<甲乙甲乙,二、填空题:本大题共6小题,每小题5分,共30分。
2024届北京市西城35中数学高一下期末统考试题含解析

2024届北京市西城35中数学高一下期末统考试题注意事项:1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑,如需改动,用橡皮擦干净后,再选涂其它答案标号。
回答非选择题时,将答案写在答题卡上,写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的1.已知扇形的面积为210cm ,半径为4cm ,则扇形的圆心角的弧度数为 A .54B .32C .34D .122.设,,a b c ∈R 且a b >,则下列不等式成立的是( ) A .c a c b -<-B .22ac bc >C .11a b< D .1b a< 3.将函数sin(2)y x ϕ=+的图象沿x 轴向左平移π8个单位,得到一个偶函数的图象,则ϕ的一个可能取值为( ) A .3π4B .π4C .π3D .π64.已知(4-2),b (cos ,sin )a ,αα==且a b ⊥,则33sin cos sin cos αααα+-为( ) A .2B .95C .3D .355.如图所示,PA 垂直于以AB 为直径的圆O 所在的平面,C 为圆上异于A B ,的任一点,则下列关系中不正确的是( )A .PA BC ⊥B .BC ⊥平面PAC C .AC PB ⊥D .PC BC ⊥6.函数的图象可由函数的图象( )A .向左平移个单位长度得到B .向左平移个单位长度得到C .向右平移个单位长度得到D .向右平移个单位长度得到7.若0a b <<,则下列不等式不成立的是( ) A .11a b> B .2ab b < C .222a b ab +> D .22a b <8.下列函数中,最小正周期为π且图象关于原点对称的函数是( ) A .cos 22y x π⎛⎫=+⎪⎝⎭B .sin 22y x π⎛⎫=+⎪⎝⎭C .sin2cos2y x x =+D .sin cos y x x =+9.函数()32cos4f x x =-的最大值为( ) A .1B .2C .3D .510.已知a 与b 均为单位向量,它们的夹角为60︒,那么3a b -等于( ) A .7B .10C .13D .4二、填空题:本大题共6小题,每小题5分,共30分。
精品解析:北京市西城区高一下学期期末数学试题(含答案)

答卷时应注意事项1、拿到试卷,要认真仔细的先填好自己的考生信息。
2、拿到试卷不要提笔就写,先大致的浏览一遍,有多少大题,每个大题里有几个小题,有什么题型,哪些容易,哪些难,做到心里有底;3、审题,每个题目都要多读几遍,不仅要读大题,还要读小题,不放过每一个字,遇到暂时弄不懂题意的题目,手指点读,多读几遍题目,就能理解题意了;容易混乱的地方也应该多读几遍,比如从小到大,从左到右这样的题;4、每个题目做完了以后,把自己的手从试卷上完全移开,好好的看看有没有被自己的手臂挡住而遗漏的题;试卷第1页和第2页上下衔接的地方一定要注意,仔细看看有没有遗漏的小题;5、中途遇到真的解决不了的难题,注意安排好时间,先把后面会做的做完,再来重新读题,结合平时课堂上所学的知识,解答难题;一定要镇定,不能因此慌了手脚,影响下面的答题;6、卷面要清洁,字迹要清工整,非常重要;7、做完的试卷要检查,这样可以发现刚才可能留下的错误或是可以检查是否有漏题,检查的时候,用手指点读题目,不要管自己的答案,重新分析题意,所有计算题重新计算,判断题重新判断,填空题重新填空,之后把检查的结果与先前做的结果进行对比分析。
亲爱的小朋友,你们好!经过两个月的学习,你们一定有不小的收获吧,用你的自信和智慧,认真答题,相信你一定会闯关成功。
相信你是最棒的!高一第二学期期末数学试卷一、选择题1. 下列各角中,与27°角终边相同的是( )A. 63° B. 153°C. 207°D. 387°【答案】D 【解析】【分析】写出与27°终边相同角的集合,取k 值得答案.【详解】与27°角终边相同的角的集合为{}27360,k k Z a a =°+×°Î,取1k =,可得387a =°.∴与27°角终边相同的是387°.故选:D【点睛】本小题主要考查终边相同的角,属于基础题.2. 圆柱的母线长为5cm ,底面半径为2cm ,则圆柱的侧面积为( )A. 220cm p B. 210cm p C. 228cm p D. 214cm p 【答案】A 【解析】【分析】根据圆柱的侧面积公式计算即可.【详解】圆柱的母线长为5cm ,底面半径为2cm ,则圆柱的侧面积为()222520cm S p p =´´=侧.故选:A【点睛】本小题主要考查圆柱的侧面积公式,属于基础题.3. sin 2p a æö+=ç÷èø( )A. sin a B. cos aC. sin a- D. cos a-【答案】B 【解析】【分析】直接利用诱导公式得答案.【详解】依题意sin cos 2p a a æö+=ç÷èø.故选:B【点睛】本小题主要考查诱导公式,属于基础题.4. 设(),a p p Î-,且1cos 2a =-,则a =( )A. 23p -或23p B. 3p-或3pC. 3p-或23pD. 23p -或3p 【答案】A 【解析】【分析】由已知角及范围,结合特殊角的三角函数值即可求解.【详解】因为(),a p p Î-,且1cos 2a =-,则23p a =-或23p.故选:A【点睛】本小题主要考查特殊角的三角函数值,属于基础题.5. 设a r ,b r均为单位向量,且14a b ×=r r ,则2a b +=r r ( )A. 3 C. 6D. 9【答案】B 【解析】【分析】利用向量的模的运算法则,结合向量的数量积求解即可.【详解】a r ,b r均为单位向量,且14a b ×=r r ,则a +==r 故选:B【点睛】本小题主要考查向量模的运算,属于基础题.6. 下列四个函数中,以p 为最小正周期,且在区间0,2p æöç÷èø上为增函数的是( )A. sin 2y x =B. cos 2y x =C. tan y x= D. sin2x y =【答案】C 【解析】【分析】利用三角函数的单调性和周期性,逐一判断各个选项是否正确,从而得出结论.【详解】解:在区间0,2p æöç÷èø上,()20,x p Î,sin 2y x =没有单调性,故排除A .在区间0,2p æöç÷èø上,()20,x p Î,cos 2y x =单调递减,故排除B .在区间0,2p æöç÷èø上,tan y x =单调递增,且其最小正周期为p ,故C 正确;根据函数以p 为最小正周期,sin 2x y =的周期为2412pp=,可排除D .故选:C .【点睛】本题考查了三角函数的性质,掌握三角函数的基本性质是解题的关键,属于基础题.7. 已知向量a v ,b v 在正方形网格中的位置如图所示,那么向量a v ,b v的夹角为( )A. 45°B. 60°C. 90°D. 135°【答案】A 【解析】【分析】根据向量的坐标表示,求得,a b r r的坐标,再利用向量的夹角公式,即可求解.【详解】由题意,可得()3,1a =r,()1,2b =r ,设向量a r ,b r的夹角为q,则cos q =,又因为0180q °££°,所以45q =°.故选:A .【点睛】本题主要考查了向量的坐标表示,以及向量夹角公式的应用,其中解答中熟记向量的坐标表示,利用向量的夹角公式,准确计算是解答的关键,着重考查了推理与运算能力,属于基础题.8. 设a ,()0,b p Î,且a b >,则下列不等关系中一定成立的是( )A. sin sin a b < B. sin sin a b> C. cos cos a b< D. cos cos a b>【答案】C 【解析】【分析】根据正弦函数以及余弦函数在()0,p 上的单调性求解即可.【详解】因a ,()0,b p Î,且a b >,而sin y x =在()0,p 上有增有减;故sin a 与sin b 大小关系不确定,cos y x =在()0,p 上单调递减;若a b >,则cos cos a b <成立;故选:C【点睛】本题主要考查了利用正余弦函数的单调性比较函数值的大小,属于基础题.9.将函数()sin 2f x x =的图象向右平移j (02pj <£)个单位,得到函数()g x 的图象.在同一坐标系中,这两个函数的部分图象如图所示,则j =( )A.6p B.4p C.3pD.2p【答案】C 【解析】【分析】由图可知,17248g f p p æöæö==ç÷ç÷èøèø()()sin 2x g x j =-,于是推出为1717sin 22424g p p j æöæö=-=ç÷ç÷èøèø1722124k p p j p -=+或324k p p +,k Z Î,再结合02p j <£,解之即可得j 的值.【详解】由图可知,17sin 22488g f pp p æöæöæö==´=ç÷ç÷ç÷èøèøèø,因为()f x 的图象向右平移j 个单位,得到函数()g x 的图象,所以()()sin 2x g x j =-,所以171717sin 2sin 2242412g pp p j j æöæöæö=-=-=ç÷ç÷ç÷èøèøèø,所以1722124k p p j p -=+或17322124k p pj p -=+,k Z Î,解得712k p j p =-或3k pj p =-,k Z Î,因02p j <£,所以3pj =.故选:C【点睛】本小题主要考查三角函数图象变换,属于中档题.10.棱锥被平行于底面的平面所截,得到一个小棱锥和一个棱台.小棱锥的体积记为y ,棱台的体积记为x ,则y 与x 的函数图象为( )A. B.C. D.【答案】A 【解析】【分析】设棱锥的体积为V ,则y V x =-,即y 是关于x 的一次函数,且单调递减,故而得解.为【详解】设棱锥的体积为V ,则V 为定值,所以y V x =-,即y 是关于x 的一次函数,且单调递减,故选:A【点睛】本小题主要考查函数图象,属于基础题.二、填空题11. 已知圆的半径为2,则5p的圆心角所对的弧长为______.【答案】25p 【解析】【分析】由已知结合弧长公式即可直接求解.【详解】由弧长公式可得2255l r pp a ==´=.故答案为:25p 【点睛】本小题主要考查弧长公式,属于基础题.12. 在平面直角坐标系xOy 中,角a 和角b 均以Ox 为始边,它们的终边关于x 轴对称.若1sin 3a =,则sin b =______.【答案】13-【解析】【分析】由题意可得()sin sin b a =-,由此能求出结果.【详解】∵在平面直角坐标系xOy 中,角a 与角b 均以Ox 为始边,它们的终边关于x 轴对称,∴()1sin sin sin 3b a a =-=-=-,故答案为:13-【点睛】本小题主要考查三角函数的对称性,属于基础题.13. 向量a r ,b r满足1b =r ,1a b ×=r r .若()a b b l -^r r r ,则实数l =______.【答案】1【解析】【分析】根据平面向量数量积的运算法则,可列出关于λ的方程,解之即可.【详解】解:∵()a b b l -^r r r ,∴()20a b b a b b l l -×=×-=r r r r r r ,即10l -=,解得1l =.故答案为:1.【点睛】本题考查了向量垂直求参数,考查了向量数量积的定义,属于基础题.14.已知正方体1111ABCD A B C D -的八个顶点在同一个球面上,若正方体的棱长是2,则球的直径是______;球的表面积是______.【答案】(1). 12p 【解析】【分析】首先求出外接球的半径,进一步求出球的表面积.【详解】解:正方体1111ABCD A B C D -的八个顶点在同一个球面上,若正方体的棱长是2,设外接球的半径为r ,则()2222222212r =++=,解得r =,故球直径为.球的表面积为2412S p p =´´=.故答案为:12p .【点睛】本题考查了多面体的外接球问题以及球的表面积公式,考查了基本运算求解能力,属于基础题.15. 已知函数()cos ,0sin ,0x x f x x x p p-£<ì=í££î给出下列三个结论:①()f x 是偶函数;②()f x 有且仅有3个零点;③()f x 的值域是[]1,1-.其中,正确结论的序号是______.的【答案】②③【解析】【分析】判断函数的奇偶性判断①;求出函数的零点判断②;函数的值域判断③.【详解】函数()cos ,0sin ,0x x f x x x p p -£<ì=í££î,①由于()()1,sin 0f fp p p -=-==,所以()f x 是非奇非偶函数,所以①不正确;②()0f x =,可得2x p=-,0x =,x p =,所以函数有且仅有3个零点;所以②正确;③函数()cos ,0sin ,0x x f x x x p p-£<ì=í££î,()f x 的值域是[]1,1-,正确;正确结论的序号是:②③.故答案为:②③.【点睛】本小题主要考查函数的奇偶性、零点、值域.16.设函数()()sin 06f x x p w w æö=+>ç÷èø,若()3f x f p æö³-ç÷èø对任意的实数x 都成立,则w 的最小值为______.【答案】2【解析】【分析】由题意可得()f x 的最小值为3f p æö-ç÷èø,可得2362k p p p w p -+=-,k Z Î,解方程可得w 的最小值.【详解】解:若()3f x f p æö³-ç÷èø对任意的实数x 都成立,可得()f x 的最小值为3f p æö-ç÷èø,可得2362k pppw p -+=-,k Z Î,即有26k w =-,k Z Î,由0>w ,可得w 的最小值为2,此时0k =.故答案为:2.【点睛】本题考查了三角函数的性质,考查了基本知识的掌握情况,属于基础题.三、解答题17. 已知0,2p a æöÎç÷èø,且4cos 5a =.(1)求tan a 的值;(2)求2sinsin 22aa +的值.【答案】(1)34;(2)5350.【解析】【分析】(1)由已知利用同角三角函数基本关系式求得sin a ,再由商的关系求得tan a ;(2)直接利用二倍角的正弦公式、降次公式求解.【详解】(1)∵0,2a p æöÎç÷èø,且4cos 5a =,∴3sin 5a ==,则sin 3tan cos 4a a a ==;(2)∵3sin 5a =,4cos 5a =,∴21cos sinsin 22sin cos 22a a a a a -+=+4134535225550-=+´´=.【点睛】本小题主要考查同角三角函数的基本关系式、二倍角公式.18. 如图,正三棱锥P ABC -的底面边长为2,侧棱长为3.(1)求正三棱锥P ABC -的表面积;(2)求正三棱锥P ABC -的体积.【答案】(1);(2【解析】【分析】(1)取BC 的中点D ,连接PD ,利用勾股定理求得PD ,可得三角形PBC 的面积,进一步可得正三棱锥P ABC -的侧面积,再求出底面积,则正三棱锥P ABC -的表面积可求;(2)连接AD ,设O 为正三角形ABC 的中心,则PO ^底面ABC .求解PO ,再由棱锥体积公式求解.【详解】(1)取BC 的中点D ,连接PD ,在Rt PBD △中,可得PD ==∴12PBC S BC PD =×=△.∵正三棱锥的三个侧面是全等的等腰三角形,∴正三棱锥P ABC -的侧面积是3PBC S =△.∵正三棱锥的底面是边长为2的正三角形,∴122sin 602ABC S =´´´°=△则正三棱锥P ABC -的表面积为;(2)连接AD ,设O 为正三角形ABC 的中心,则PO ^底面ABC .且13OD AD ==.在Rt POD V 中,PO ==.∴正三棱锥P ABC -的体积为13ABC S PO ×=△【点睛】本小题主要考查锥体的表面积和体积的求法,属于中档题.19. 在ABC V 中,角A ,B ,C 所对的边分别为a ,b ,c ,且34C p =,sin A =.(1)求sin B 的值;(2)若5c a -=,求ABC V 的面积.【答案】(12)52.【解析】【分析】(1)先根据sin A =cos A 的值,再由4B A p =-得到sin sin 4B A p æö=-ç÷èø,根据两角和与差的公式可求得sin B 即可;(2)由34C p =可求得sin C 的值,进而根据正弦定理可求得a ,c 的关系,再由5c a -=-可求出a ,c 的值,最后利用三角形的面积公式即得结果.【详解】解:(1)因为34C p =,sin A =,所以cos A ==由已知得4B A p=-.所以sin sin sin cos cos sin 444B A A A p p p æö=-=-==ç÷èø(2)由(1)知34C p =,所以sin C =且sin B =由正弦定理得sin sin a A c C ==.又因为5c a -=-,所以5c =,a =.所以15sin 522ABC S ac B ===△.【点睛】本题考查了三角形的正弦定理和面积公式,考查了同角三角关系和两角和与差的正弦公式,属于中档题.20. 已知函数()cos2sin cos x f x x x=+.(1)求()f x 的定义域;(2)求()f x 在区间02p éùêúëû,上的最大值;(3)求()f x 的单调递减区间.【答案】(1)|,4x x k k Z p p ìü¹-Îíýîþ;(2)1;(3)()32,244k k k Z p p p p éù-+Îêúëû.【解析】【分析】(1)由分母不为零得到sin cos 0x x +¹04x p æö+¹ç÷èø求解.(2)利用二倍角公式和辅助角法,将函数转化为()4f x x p æö=+ç÷èø,再利用余弦函数的性质求解. (3)由(2)知()4f x x p æö=+ç÷èø,利用余弦函数的性质,令 224k x k p p p p £+£+求解.【详解】(1)因sin cos 0x x +¹04x p æö+¹ç÷èø,解得4x k pp +¹,所以()f x 的定义域是|,4x x k k Z p p ìü¹-Îíýîþ为(2)因为()22cos2cos sin sin cos sin cos x x x f x x x x x-==++,cos sin x x =-,4x p æö=+ç÷èø又0,2x p éùÎêúëû,所以3,444x p p p éù+Îêúëû,cos 4x p éæö+Îêç÷èøë,所以()f x 区间02p éùêúëû,上的最大值是1;(3)令 224k x k p p p p £+£+,解得 32244k x k p p p p -££+, 所以()f x 的单调递减区间.是()32,244k k k Z p p p p éù-+Îêúëû【点睛】本题主要考查函数定义域的求法,二倍角公式,辅助角法以及三角函数的性质,还考查了转化求解问题的能力,属于中档题.21. 如图,在正方体1111ABCD A B C D -中,E 为1CC 的中点.(1)在图中作出平面1AD E 和底面ABCD 的交线,并说明理由;(2)平面1AD E 将正方体分成两部分,求这两部分的体积之比.【答案】(1)答案见解析;(2)7:17.【解析】【分析】(1)在正方形11DCC D 中,直线1D E 与直线DC 相交,设1D E DC F Ç=,连接AF ,可证F Î平面ABCD 且F Î平面1AD E ,得到平面1AD E Ç平面ABCD AF =;(2)设BC AF G Ç=,连接GE ,证明1//EG AD ,则平面1AD E 将正方体分成两部分,其中一部分是三棱台1CGE DAD -.设正方体1111ABCD A B C D -的棱长为2.求出棱台1CGE DAD -的体积,由正方体体积减去棱台体积可得另一部分几何体的体积作比得答案.【详解】(1)在正方形11DCC D 中,直线1D E 与直线DC 相交,设1D E DC F Ç=,连接AF ,∵F DC Î,DC Ì平面ABCD ,则F Î平面ABCD ,∵1F D E Î,1D E Ì平面1AD E ,∴F Î平面1AD E .∴平面1AD E Ç平面ABCD AF =.(2)设BC AF G Ç=,连接GE ,由E 为1CC 的中点,得G 为BC 的中点,∴1//EG AD ,则平面1AD E 将正方体分成两部分,其中一部分是三棱台1CGE DAD -.设正方体1111ABCD A B C D -的棱长为2.1111-77178833F DAD F CGE F DAD DAD CGE DAD V V V S FD ---=-==´´=△棱台.∴另一部分几何体的体积为3717233-=.∴两部分的体积比为7:17【点睛】本小题主要考查面与面位置关系,考查几何体体积的求法.22. 如图,在扇形OAB 中,120AOB Ð=°,半径2OA OB ==,P 为弧AB 上一点.(1)若OA OP ^,求PA PB ×uuu r uuu r 的值;(2)求PA PB ×uuu r uuu r 的最小值.【答案】(1)2-;(2)2-.【解析】【分析】(1)先通过倒角运算得出30POB Ð=°,120APB Ð=°,再在POB V中,由余弦定理可求得PB =uuu r cos PA PB PA PB APB ×=×Ðuuu r uuu r uuu r uuu r ,代入数据进行运算即可得解;(2)以O 为原点,OA 所在直线为x 轴建立平面直角坐标系,设()2cos ,2sin P a a ,其中20,3p a éùÎêúëû,结合平面向量数量积的坐标运算,用含有a 的式子表示出PA PB ×uuu r uuu r,再利用三角恒等变换公式和正弦函数的图象即可得解.【详解】(1)当OA OP ^时,如图所示,的∵120AOB Ð=°,∴1209030POB Ð=°-°=°,18030752OPB °-°Ð==°,∴7545120APB Ð=°+°=°,在POB V中,由余弦定理,得222222cos 22222cos308PB OB OP OB OP POB =+-×Ð=+-´´´°=-∴PB ==uuu r ,又PA OA ==uuu r ,∴1cos 22PA PB PA PB APB æö×=×Ð=´-=-ç÷èøuuu r uuu r uuu r uuu r (2)以O 为原点,OA 所在直线为x 轴建立如图所示的平面直角坐标系,则()2,0A ,∵120AOB Ð=°,2OB =,∴(B -,设()2cos ,2sin P a a ,其中20,3p a éùÎêúëû,则()()22cos ,2sin 12cos 2sin PA PB a a a a ×=--×---uuu r uuur 2222cos 4cos 4sin a a a a=--+-+2cos 24sin 26p a a a æö=--+=-++ç÷èø.∵20,3p a éùÎêúëû,∴5,666p p p a éù+Îêúëû,1sin ,162p a æöéù+Îç÷êúèøëû,∴当62ppa +=,即3pa =时,PA PB ×uuu r uuu r取得最小值为2-.【点睛】本题考查平面向量的坐标表示,考查平面向量的数量积,考查余弦定理,考查三角函数的图象与性质,属于中档题.。
2024届北京市西城区第14中学数学高一第二学期期末综合测试模拟试题含解析

2024届北京市西城区第14中学数学高一第二学期期末综合测试模拟试题考生须知: 1.全卷分选择题和非选择题两部分,全部在答题纸上作答。
选择题必须用2B 铅笔填涂;非选择题的答案必须用黑色字迹的钢笔或答字笔写在“答题纸”相应位置上。
2.请用黑色字迹的钢笔或答字笔在“答题纸”上先填写姓名和准考证号。
3.保持卡面清洁,不要折叠,不要弄破、弄皱,在草稿纸、试题卷上答题无效。
一、选择题:本大题共10小题,每小题5分,共50分。
在每个小题给出的四个选项中,恰有一项是符合题目要求的 1.为了得到函数y sin 23x π⎛⎫=+⎪⎝⎭的图象,只需把函数sin 2y x =的图象( ) A .向左平移6π个单位长度 B .向右平移6π个单位长度 C .向左平移3π个单位长度D .向右平移3π个单位长度2.已知sin()sin()m αβαβ-=+,且tan 2tan 0αβ=≠,则实数m 的值为( ) A .2B .12C .3D .133.已知直线1l :10x ay +-=,2l :(1)0a x ay +-=,若p :12l l //;:2q a =-,则p 是q 的( )A .充要条件B .充分不必要条件C .必要不充分条件D .既不充分也不必要条件4.一游客在A 处望见在正北方向有一塔B ,在北偏西45︒方向的C 处有一寺庙,此游客骑车向西行1km 后到达D 处,这时塔和寺庙分别在北偏东30和北偏西15︒,则塔B 与寺庙C 的距离为( ) A .2kmB .3kmC .2kmD .1km5.某几何体的三视图如图所示,则该几何体的表面积为( )A .7616π+B .6012π+C .4416π+D .4412π+6.直线3230x y -+=被圆224x y +=截得的劣弧与优弧的长之比是( ) A .1:5B .1:2C .1:3D .1:47.执行如图所示的程序,已知i 的初始值为1,则输出的S 的值是( )A .5B .9C .13D .178.天气预报说,在今后的三天中,每一天下雨的概率均为40%.现采用随机模拟试验的方法估计这三天中恰有两天下雨的概率:先利用计算器产生0到9之间取整数值的随机数,用1,2,3,4表示下雨,用5,6,7,8,9,0表示不下雨;再以每三个随机数作为一组,代表这三天的下雨情况.经随机模拟试验产生了如下20组随机数: 907 966 191 925 271 932 812 458 569 683 431 257 393 027 556 488 730 113 537 989 据此估计,这三天中恰有两天下雨的概率近似为 A .0.35B .0.25C .0.20D .0.159.ABC ∆中,若cos c a B =⋅,则ABC ∆的形状是( ) A .等腰三角形 B .等边三角形 C .锐角三角形 D .直角三角形10.若 则( ) A .B .C .D .二、填空题:本大题共6小题,每小题5分,共30分。
2022北京西城区高一下学期期末数学试题和答案

2022北京西城高一(下)期末数 学一、选择题共10小题,每小题4分,共40分。
在每小题列出的四个选项中,选出符合题目要求的一项。
1.(4分)在复平面内,复数2z i i =+对应的点在( ) A .第一象限B .第二象限C .第三象限D .第四象限2.(4分)设向量(3,1)a =,(1,2)b =−,则(2)(a b b −⋅= ) A .11−B .9−C .7−D .5−3.(4分)设m ,n 为两条直线,α,β为两个平面.若//αβ,//m n ,m α⊥,则( ) A .//n β B .n β⊥C .//m βD .以上答案都不对4.(4分)若3cos 5α=,则3sin()(2πα−= )A .35B .35−C .45 D .45−5.(4分)函数()sin(2)6f x x π=+,[0x ∈,]2π的最大值和最小值分别为( )A .1,1−B .11,22−C .1,12 D .1,12−6.(4分)在ABC ∆中,若222a b c kab +−=,则实数k 的取值范围是( ) A .(2,2)−B .(1,1)−C .1(2−,1)2D .(0,1)7.(4分)已知向量a ,b 满足||4a =,||2b =,()a b b +⊥,那么向量a ,b 的夹角为( ) A .6πB .3π C .23π D .56π 8.(4分)函数1cos 2()sin xf x x−=的图像( )A .关于原点对称B .关于y 轴对称C .关于直线x π=对称D .关于点(2π,0)对称9.(4分)设(,)αππ∈−,则“(4πα∈−,3)4π”是“sin cos 0αα+>”的( ) A .充分而不必要条件 B .必要而不充分条件 C .充分必要条件D .既不充分也不必要条件10.(4分)如图,正方形ABCD 的边长为2,P 为正方形ABCD 四条边上的一个动点,则PA PB ⋅的取值范围是( )A .[1−,2]B .[0,2]C .[0,4]D .[1−,4]二、填空题共5小题,每小题5分,共25分。
2024届北京市西城区北京师大附属实验中学数学高一第二学期期末复习检测模拟试题含解析
2024届北京市西城区北京师大附属实验中学数学高一第二学期期末复习检测模拟试题注意事项1.考试结束后,请将本试卷和答题卡一并交回.2.答题前,请务必将自己的姓名、准考证号用0.5毫米黑色墨水的签字笔填写在试卷及答题卡的规定位置. 3.请认真核对监考员在答题卡上所粘贴的条形码上的姓名、准考证号与本人是否相符. 4.作答选择题,必须用2B 铅笔将答题卡上对应选项的方框涂满、涂黑;如需改动,请用橡皮擦干净后,再选涂其他答案.作答非选择题,必须用05毫米黑色墨水的签字笔在答题卡上的指定位置作答,在其他位置作答一律无效.5.如需作图,须用2B 铅笔绘、写清楚,线条、符号等须加黑、加粗.一、选择题:本大题共10小题,每小题5分,共50分。
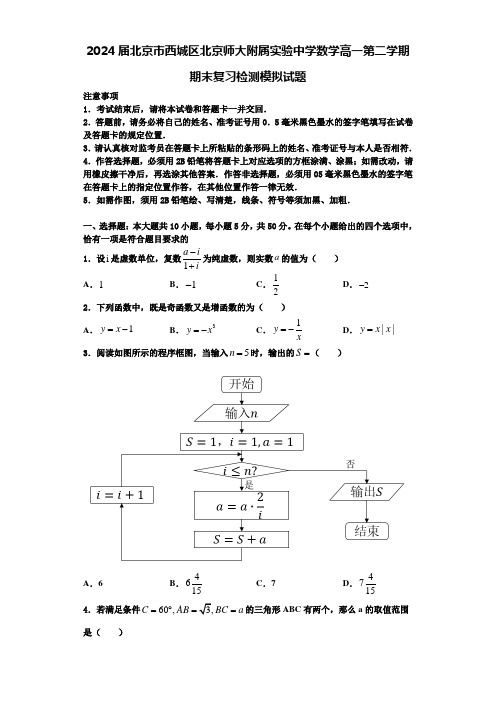
在每个小题给出的四个选项中,恰有一项是符合题目要求的 1.设i 是虚数单位,复数1a ii-+为纯虚数,则实数a 的值为( ) A .1B .1-C .12D .2-2.下列函数中,既是奇函数又是增函数的为( ) A .1y x =-B .3y x =-C .1y x=-D .||y x x =3.阅读如图所示的程序框图,当输入5n =时,输出的S =( )A .6B .4615C .7D .47154.若满足条件60,3,C AB BC a =︒==的三角形ABC 有两个,那么a 的取值范围是( )A .()1,2B .()2,3C .()3,2D .()1,25.已知数列{}n a 的通项公式是23n a n =-,则该数列的第五项是( ) A .13-B .13C .11-D .16-6.盒中装有除颜色以外,形状大小完全相同的3个红球、2个白球、1个黑球,从中任取2个球,则互斥而不对立的两个事件是( ) A .至少有一个白球;至少有一个红球 B .至少有一个白球;红、黑球各一个 C .恰有一个白球:一个白球一个黑球D .至少有一个白球;都是白球7.若数列{}n a 前12项的值各异,且12n n a a +=对任意的*n N ∈都成立,则下列数列中可取遍{}n a 前12项值的数列为( ) A .31{}k a + B .41{}k a +C .51{}k a +D .61{}k a + 8.在中,角、、所对的边分别为、、,,,,则( )A .B .C .D .9.函数()()2f x sin x ωϕ+=(0ω>,22ππϕ-<<)的部分图象如图所示,则ωϕ,的值分别是( )A .2,3π-B .2,6π-C .4,6π-D .4,3π10.圆22240x y x y +-+=与直线()2220tx y t t R ---=∈的位置关系为( )A .相离B .相切C .相交D .以上都有可能二、填空题:本大题共6小题,每小题5分,共30分。
2022-2023学年北京市西城区高一上册数学期末试题(含解析)

2022-2023学年北京市西城区高一上册数学期末试题(含解析)一、单选题1.已知集合{}2{|51},9A x x B x x =-≤<=≤,则A B ⋃=()A .[5,3]-B .(3,1]-C .[3,1)-D .[3,3]-【答案】A【分析】先化简集合B ,再求并集即可.【详解】因为{}2]|9[3,3B x x ==-≤,所以[5,3]A B ⋃=-.故选:A2.已知命题p :∃x <1,21x ≤,则p ⌝为A .∀x ≥1,2x >1B .∃x <1,21x >C .∀x <1,21x >D .∃x ≥1,21x >【答案】C【详解】根据全称命题与存在性命题之间的关系,可知命题2:1,1p x x ∃<≤的否定为21,1x x ∀<>,故选C .3.如图,在平行四边形ABCD 中,AC AB -=()A .CB B .ADC .BD D .CD【答案】B【分析】根据向量运算得AC AB AD -=.【详解】由图知AC AB BC AD -==,故选:B.4.若a b >,则下列不等式一定成立的是()A .11a b <B .22a b >C .e e a b--<D .ln ln a b>【答案】C【分析】利用特殊值判断AB ,由不等式的性质及指数函数的单调性判断C ,由特殊值及对数的意义判断D.【详解】当1,1a b ==-时,11a b>,故A 错误;当1,1a b ==-时,22a b =,故B 错误;由a b a b >⇒-<-,因为e x y =为增函数,所以e e a b --<,故C 正确;当1,1a b ==-时,ln b 无意义,故ln ln a b >不成立,故D 错误.故选:C 5.不等式2112x x +≤-的解集为()A .[3,2]-B .(,3]-∞-C .[3,2)-D .(,3](2,)-∞-+∞ 【答案】C【分析】将不等式移项通分得到302x x +≤-,再转化为二次不等式即可得答案.【详解】21310022x x x x ++-≤⇒≤--,即(3)(2)0(20)x x x +-≤-≠,解得:32x -≤<,∴不等式的解集为[3,2)-,故选:C.6.正方形ABCD 的边长为1,则|2|AB AD +=()A .1B .3CD【答案】D【分析】利用向量数量积的运算性质,结合正方形中垂直关系及边长即可求解.【详解】在正方形ABCD 中,如图所示,2222|2|(2)441045AB AD AB AD AB AB AD AD +=+=+⋅+=++= ,2AB AD ∴+=故选:D.7.某物流公司为了提高运输效率,计划在机场附近建造新的仓储中心.已知仓储中心建造费用C (单位:万元)与仓储中心到机场的距离s (单位:km )之间满足的关系为80022000C s s=++,则当C 最小时,s 的值为()A .20B .C .40D .400【答案】A【分析】根据均值不等式求解即可.【详解】因为8002200020002080C s s =++≥=,当且仅当8002s s=,即20s =时等号成立,所以当C 最小时,s 的值为20.故选:A8.设2log 3a =,则122a +=()A .8B .11C .12D .18【答案】D【分析】计算22log 9a =,122222a a +=⨯,代入计算即可.【详解】2log 3a =,则2222log 3log 9a ==,22log 91228a a+=⨯=⨯=⨯=,故选:D.9.己知a为单位向量,则“||||1a b b +-= ”是“存在0λ>,使得b a λ= ”的()A .充分而不必要条件B .必要而不充分条件C .充分必要条件D .既不充分也不必要条件【答案】B【分析】对于前者是否能推出后者,我们举出反例0b =即可,对于后者是否推前者,由后者可得,a b共线且同方向,则||||||1a b b a b b a +-=+-==,即后者能推出前者,最后即可判断.【详解】若0b = ,则||||1a b b a +-== ,但此时不存在0λ>,使得b a λ=,故不存在0λ>,使得b a λ=,故前者无法推出后者,若存在0λ>,使得b a λ=,则,a b 共线且同方向,此时||||||1a b b a b b a +-=+-==,故后者可以推出前者,故“||||1a b b +-= ”是“存在0λ>,使得b a λ=的必要不充分条件”,故选:B.10.近年来,踩踏事件时有发生,给人们的生命财产安全造成了巨大损失.在人员密集区域,人员疏散是控制事故的关键,而能见度x (单位:米)是影响疏散的重要因素.在特定条件下,疏散的影响程度k 与能见度x 满足函数关系:0.2,0.11.4,0.1101,10bx k ax x x <⎧⎪=+≤≤⎨⎪>⎩(,a b 是常数).如图记录了两次实验的数据,根据上述函数模型和实验数据,b 的值是(参考数据:lg 30.48≈)()A .0.24-B .0.48-C .0.24D .0.48【答案】A【分析】分别代入两点坐标得0.1 1.2b a ⋅=-,100.4b a ⋅=-,两式相比得结合对数运算得lg32b =-,解出b 值即可.【详解】当0.1x =时,0.1 1.40.20.1 1.2b b a a ⋅+=⇒⋅=-①,当10x =时,10 1.41100.4b b a a ⋅+=⇒⋅=-②,①比②得0.113310100bb b ⎛⎫=⇒⇒ ⎪⎝⎭,()22103103bb --∴=⇒=,lg30.48lg320.2422b b ∴=-⇒=-≈-=-故选:A.二、填空题11.函数2()log (1)f x x =-的定义域是_____________.【答案】[0,1)【分析】根据对数型函数的定义域,结合二次根式的性质进行求解即可.【详解】由题意可知:10010x x x ->⎧⇒≤<⎨≥⎩,所以该函数的定义域为[0,1),故答案为:[0,1)12.某高校调查了200名学生每周的自习时间(单位:小时),制成了如图所示的频率分布直方图,其中自习时间的范围是[]12.5,25,样本数据分组为[)12.5,15,[)15,17.5,[)17.5,20,[)20,22.5,[]22.5,25.根据频率分布直方图,这200名学生中每周的自习时间不少于20小时的人数是________________.【答案】60【分析】首先计算频率为0.3,再乘以总人数即可.【详解】由频率分布直方图可知每周自习时间不少于20小时的频率为(0.080.04) 2.50.3+⨯=,故200名学生中每周的自习时间不少于20小时的人数为2000.360⨯=人.故答案为:60.13.写出一个同时满足下列两个条件的函数()f x =_____________.①对12,(0,)x x ∀∈+∞,有()()()1212f x x f x f x =+;②当(4,)x ∈+∞时,()1f x >恒成立.【答案】2l og x (答案不唯一)【分析】由()f x 满足的两个条件可以联想到对数函数,再根据对数函数的性质时行判断即可得答案.【详解】解:因为由()f x 满足的两个条件可以联想到对数函数,当2()log f x x =时,对12,(0,)x x ∀∈+∞,()12212212212log ()log log ()()f x x x x x x f x f x ==+=+,满足条件①;当(4,)x ∈+∞时,2()log 421f x >=>,满足条件②.故答案为:2l og x (答案不唯一)14.函数()f x 的定义域为R ,且x ∀∈R ,都有1()()f x f x -=,给出给出下列四个结论:①(0)1f =或1-;②()f x 一定不是偶函数;③若()0f x >,且()f x 在(,0)-∞上单调递增,则()f x 在(0,)+∞上单调递增;④若()f x 有最大值,则()f x 一定有最小值.其中,所有正确结论的序号是______________.【答案】①③【分析】根据所给性质直接计算可判断①,取特殊函数判断②,利用函数的单调性定义判断③,取特殊函数判断④.【详解】因为x ∀∈R ,都有1()()f x f x -=,所以1(0)(0)f f =,即(0)1f =或1-,故①正确;不妨取()1f x =,则1()1()f x f x -==,即()()f x f x -=恒成立,所以()f x 是偶函数,故②错误;设12,(0,)x x ∀∈+∞,且12x x <,则210x x -<-<,所以21()()f x f x -<-,即21110()()f x f x <<,所以12()()f x f x <,即()f x 在(0,)+∞上单调递增,故③正确;不妨取,0()1,01,0x x f x x x x⎧⎪<⎪==⎨⎪⎪->⎩,则满足1()()f x f x -=,函数有最大值1,但是无最小值,故④错误.故答案为:①③三、双空题15.已知函数()2,0,0x a x f x ax x ⎧+≥=⎨<⎩,若4a =-,则()0f x >的解集为___________;若x ∀∈R ,()0f x >,则a 的取值范围为_____________.【答案】{|0x x <或}2x >;10a -<<.【分析】代入4a =-,分0x ≥和0x <两种情况,分别求解()0f x >,最后取并集即可得出()0f x >的解集;原题等价于“当0x ≥时,20x a +>恒成立”以及“当0x <时,0ax >恒成立”同时满足,分别求出a 的取值范围,最后取公共部分即可得到.【详解】当4a =-时,()24,04,0x x f x x x ⎧-≥=⎨-<⎩.当0x ≥时,由()0f x >可得240x ->,解得2x >;当0x <时,由()0f x >可得40x ->,解得0x <.综上所述,()0f x >的解集为{|0x x <或}2x >.“若x ∀∈R ,()0f x >”等价于“当0x ≥时,20x a +>恒成立”以及“当0x <时,0ax >恒成立”同时满足.当0x ≥时,20x a +>恒成立,因为当0x ≥时,2x y a =+单调递增,所以应满足0210a a +=+>,即1a >-;当0x <时,0ax >恒成立,则a<0.则由“当0x ≥时,20x a +>恒成立”以及“当0x <时,0ax >恒成立”同时满足可得,10a -<<.故答案为:{|0x x <或}2x >;10a -<<.四、解答题16.某射手打靶命中9环、10环的概率分别为0.25,0.2.如果他连续打靶两次,且每次打靶的命中结果互不影响.(1)求该射手两次共命中20环的概率;(2)求该射手两次共命中不少于19环的概率.【答案】(1)0.04(2)0.14【分析】(1)根据相互独立事件概率的乘法公式即可求解,(2)分类讨论,结合独立事件的概率公式即可求解.【详解】(1)两次共命中20环,意味着两次都是命中10环,根据相互独立事件的概率公式可得概率为:00202004P ...=´=(2)第一次9环第二次10环的概率为102502005P ...=´=,第一次10环第二次9环的概率为202025005P ...=´=,两次都是10环的概率为00202004P ...=´=,所以两次共命中不少于19环的概率为120005005004014P P P P ....=++=++=17.已知函数2()1xf x x =+.(1)判断函数()f x 的奇偶性,并证明你的结论;(2)证明函数()f x 在[1,)+∞上是减函数;(3)写出函数()f x 在(,1]-∞-上的单调性(结论不要求证明).【答案】(1)()f x 为奇函数,证明见解析(2)证明见解析(3)函数()f x 在(,1]-∞-上的单调递减【分析】(1)根据函数奇偶性的定义判断与证明即可;(2)根据单调性的定义,取值、作差(变形)、定号、下结论等步骤进行证明即可;(3)结合函数的奇偶性与单调性直接判断即可.【详解】(1)解:()f x 为奇函数,理由如下:函数2()1xf x x =+,定义域为R ,所以x ∈R ,R x -∈则()()22()11xxf x f x x x --==-=-+-+,所以()f x 为奇函数.(2)证明:任取12,[1,)x x ∈+∞,且12x x <,则()()()()()()22122112121212122222221212121()()111111x x x x x x x x x x x x f x f x x x x x x x --+---=-==++++++,因为211x x >>,所以21120,10x x x x ->->所以12())0(f x f x ->,即12()()f x f x >,故函数()f x 在[1,)+∞上是减函数.(3)解:由(1)知函数()f x 为R 上的奇函数,由(2)知函数()f x 在[1,)+∞上是单调递减所以函数()f x 在(,1]-∞-上的单调递减.18.甲和乙分别记录了从初中一年级(2017年)到高中三年级(2022年)每年的视力值,如下表所示2017年2018年2019年2020年2021年2022年甲 4.94 4.90 4.95 4.82 4.80 4.79乙4.864.904.864.844.744.72(1)计算乙从2017年到2022年这6年的视力平均值;(2)从2017年到2022年这6年中随机选取2年,求这两年甲的视力值都比乙高0.05以上的概率;(3)甲和乙的视力平均值从哪年开始连续三年的方差最小?(结论不要求证明)【答案】(1)4.82(2)25(3)甲的视力平均值从2020开始连续三年的方差最小,乙的视力平均值从2017开始连续三年的方差最小.【分析】(1)利用平均数公式计算即可;(2)列表分析,利用古典概型概率公式计算即可(3)由表中数据分析波动性即可得结论.【详解】(1)乙从2017年到2022年这6年的视力平均值为:4.86 4.90 4.86 4.84 4.74 4.724.826+++++=.(2)列表:2017年2018年2019年2020年2021年2022年甲 4.94 4.90 4.95 4.82 4.80 4.79乙 4.864.904.864.844.744.72甲与乙视力值的差0.0800.090.02-0.060.07由表格可知:2017年到2022年这6年中随机选取2年,这两年甲的视力值都比乙高0.05上的年份由有4年,故所求概率为:2426C 62C 155P ===(3)从表格数据分析可得:甲的视力平均值从2020开始连续三年的方差最小,乙的视力平均值从2017开始连续三年的方差最小.19.函数()|1lg |f x x c =--,其中c ∈R .(1)若0c =,求()f x 的零点;(2)若函数()f x 有两个零点()1212,x x x x <,求124x x +的取值范围.【答案】(1)10x =(2)[)40+¥,【分析】(1)令()0f x =,即可求解零点,(2)令()|1lg |=0f x x c =--得111210,10c c x x -++==,进而结合基本不等式即可求解.【详解】(1)当0c =时,()|1lg |f x x =-,令()0f x =,则lg 1x =,故10x =,所以()f x 的零点为10x =.(2)令()|1lg |=0f x x c =--,则|1lg |x c -=,()0c >,故1lg x c -=±,由于12x x <,所以111210,10c c x x -++==,因此1112441010=40101010c c c c x x -++-+=⨯+⨯+⨯,由于100,100c c ->>,由基本不等式可得124=40101010c c x x -+⨯+⨯≥,当且仅当4010=1010c c -⨯⨯,即lg 2c =时取等号,故12440x x +≥,所以124x x +的取值范围为[)40+¥,20.某商贸公司售卖某种水果.经市场调研可知:在未来20天内,这种水果每箱的销售利润r (单位:元)与时间t (120,t t ≤≤∈N ,单位:天)之间的函数关系式为1104r t =+,且日销售量p (单位:箱)与时间t 之间的函数关系式为1202p t =-.(1)求第几天的日销售利润最大?最大值是多少?(2)在未来的这20天中,在保证每天不赔本的情况下,公司决定每销售1箱该水果就捐赠()m m *∈N元给“精准扶贫”对象,为保证销售积极性,要求捐赠之后每天的利润随时间t 的增大而增大,求m 的取值范围.【答案】(1)第10天的销售利润最大,最大值是1250元.(2)510m ≤≤,且*N m ∈.【分析】(1)通过计算得21()(10)12502f t rp t ==--+,根据二次函数最值即可得到答案;(2)计算21()(102)12001202g t t m t m =-+++-,根据题意得到不等式10219.5m +>,且1104m +≤对于120,N t t *∈≤≤均成立以及N m *∈,最后取交集即可.【详解】(1)设第t 日的销售利润为()f t ,则1()(10)(1202)4f t rp t t ==+-211012002t t =-++21(10)12502t =--+.120,t t ≤≤∈N ,当10t =时,max ()1250f t =.所以第10天的销售利润最大,最大值是1250元.(2)设捐赠之后第t 日的销售利润为()g t ,则1()(10)(1202)4g t t m t =+--21(102)12001202t m t m =-+++-.依题意,m 应满足以下条件:①N m *∈;②192010219.52m ++>=,即 4.75m >;③1104m t +≤对于120,N t t ∈≤≤均成立,即10.25m ≤.综上510m ≤≤,且*N m ∈.21.设函数()f x 的定义域为D ,对于区间[,](,)I a b a b I D =<⊆,若满足以下两条性质之一,则称I 为()f x 的一个“Ω区间”.性质1:对任意x I ∈,有()f x I ∈;性质2:对任意x I ∈,有()f x I ∉.(1)分别判断区间[]1,2是否为下列两函数的“Ω区间”(直接写出结论);①3y x =-;②3y x=;(2)若[,]()m m >00是函数2()2f x x x =-+的“Ω区间”,求m 的取值范围;(3)已知定义在R 上,且图象连续不断的函数()f x 满足:对任意12,x x ∈R ,且12x x ≠,有()()21211f x f x x x -<--.求证:()f x 存在“Ω区间”,且存在0x ∈R ,使得0x 不属于()f x 的所有“Ω区间”.【答案】(1)①是,②不是;(2)[1,2]m ∈;(3)证明见解析.【分析】(1)根据新定义直接判断即可得出结论;(2)根据[,]()m m >00是函数2()2f x x x =-+的“Ω区间”确定其满足性质1,据此分类讨论求二次函数值域,检验即可得解;(3)由所给函数性质分析出满足性质2,转化为()f x x =不恒成立,()f x 存在“Ω区间”,再构造函数()()g x f x x =-,证明有唯一零点,且0x I ∉.【详解】(1)对①,当[1,2]x ∀∈,3[1,2]y x =-∈,满足性质1,[]1,2是函数的“Ω区间”,对②,当1x =时,3[1,2]y =∉,当2x =时,3[1,2]2y =∈,故不满足性质1,2,[]1,2不是函数的“Ω区间”.(2)记[,]()I m m =>00,{()|}S f x x I =∈,注意到(0)0[0,]f m =∈,因此,若I 为函数()f x 的“Ω区间”,则其不满足性质②,必满足性质①,即S I ⊆.22()2(1) 1.f x x x x =-+=--+当01m <<时,()f x 在I 上单调递增,且()(1)0f m m m m -=-->,所以[0,()]S f m =不包含于[,]I m =0,不合题意;当12m ≤≤时,()()][[0,1]0,10,S f f m I ⎡⎤==⊆=⎣⎦,符合题意;当m>2时,()(2)(0)0f m f f <==,所以()f m I ∉,不合题意.综上,[1,2]m ∈.(3)对于任意区间[,]()I a b a b =<,记{()|}S f x x I =∈,依题意,()f x 在I 上单调递减,则][(),()S f b f a =.因为()()1f b f a b a-<--,所以()()f a f b b a ->-,即S 的长度大于I 的长度,故不满足性质①.因此,如果I 为()f x 的“Q 区间”,只能满足性质②,即S I =∅ ,即只需存在R a ∈使得()f a a <,或存在R b ∈使得()f b b >.因为()f x x =不恒成立,所以上述条件满足,所以()f x 一定存在“Q 区间".记()()g x f x x =-,先证明函数()g x 有唯一零点;因为()f x 在R 上单调递减,所以()g x 在R 上单调递减.若(0)0f =,则00x =为()g x 的唯一零点;若(0)0f t =>,则()(0)f t f t <=,即(0)0,()0g g t ><,由零点存在定理,结合()g x 单调性,可知存在唯一0(0,)x t ∈,使得0()0g x =;若(0)0f t =<,则()(0)f t f t >=,即(0)0,()0g g t <>,由零点存在定理,结合()g x 单调性,可知存在唯一0(,0)x t ∈,使得0()0g x =;综上,函数()g x 有唯一零点0x ,即00()f x x =,已证()f x 的所有“Q 区间”I 都满足条件②,所以0x I ∉.【点睛】关键点点睛:根据所给函数的新定义,理解应用新定义,是解决问题的关键,其中注意分类讨论思想、特殊化思想的应用,属于难题.。
