Bi2Se3自旋轨道耦合计算

合集下载

Bi2Se3拓扑绝缘体材料的电子结构研究

毕业论文题目：Bi2Se3拓扑绝缘体材料的电子结构研究院（系）：年级：专业：物理学班级：学号：姓名：指导教师：完成日期：摘要采用基于第一性原理的赝势平面波方法系统地计算了Bi2Se3基态的电子结构、态密度和能带结构以及理论模型，为Bi2Se3的设计与应用提供了理论依据.计算结果表明Bi2Se3属于间接带隙半导体, 禁带宽度为0.3 eV,其能带图中有18条价带，6条导带; 其价带主要由Se的6p以及Bi的6p态电子构成,导带主要由Mg的6p以及Si的6p态电子构成;其能带图中有18条价带，6条导带.关键词Bi2Se3 第一性原理电子结构理论模型态密度能带结构一、引言按照导电性质的不同，材料可分为“金属”和“绝缘体”两大类；而更进一步，根据电子态的拓扑性质的不同“绝缘体”和“金属”还可以进行更细致的划分。

拓扑绝缘体就是根据这样的新标准而划分的区别于普通绝缘体的一类新型绝缘体材料。

它的体内与普通绝缘体一样，是绝缘的，但是在它的边界或表面总是存在导电的边缘态，这也是它有别于普通绝缘体的最独特的性质.这样的导电边缘态是稳定存在的，且不同自旋的导电电子的运动方向是相反的,传统上固体材料可以按照其导电性质分为绝缘体和导体，其中绝缘体材料在它的费米能处存在着有限大小的能隙，因而没有自由载流子；金属材料在费米能级处存在着有限的电子态密度，进而拥有自由载流子,信息的传递可以通过电子的自旋，而不像传统导电材料通过电荷，这样不涉及能量耗散过程，从而克服了传统材料的发热问题。

拓扑绝缘体作为一种新的量子物质态，完全不同于传统意义上的金属和绝缘体，其体电子结构为有带隙的绝缘体，但表面或边界却为无带隙的金属态.近年来，拓扑绝缘体因其独特的物理性质及良好的应用前景在凝聚态物理和材料科学领域引起了广泛的研究.到目前为止，用于制作纳米材料的方法有很多种，如快速凝固技术[1]、分离法[2]、球磨法[3]、表面活性合成法[4]和热还原法[5]，等等. 与这些方法相比，水热合成法有很多优势，它具有较低的成本和较高的效率，而且不需要高纯度的原材料[6]，热压的样品在623K和80MPa具有高密度，高导电率和模式。

Bi2Se3

ｓｅ３、Ｂｉ２Ｔｅ３和ｓｂ２Ｔｅ３的结构，计算它们的声子谱及热力学性质．基于广义梯度交换相关泛函及ＳＯＣ效应，计算得到三
种物质的声子频率比不考虑ＳＯＣ时更吻合实验数据．最后计算出三种物质的赫尔姆赫兹自由能Ｆ，内能Ｅ，等体热容ｃ和熵Ｓ随温度的变化趋势．关键词：第一性原理；声子谱；热力学性质；自旋一轨道耦合
２．ＳｃｈｏｏｌｏｆＥｌｅｃｔｉｒｃａｌａｎｄＩｎｆｏｒｍａｔｉｏｎＥｎｇｉｎｅｅｒｉｎｇ，ＳｏｕｔｈｗｅｓｔＵｎｉｖｅｒｓｉｔｙｏｒｆＮａｔｉｏｎｌａｉｔｉｅｓ，Ｃｈｅｎｇｄｕ６１００４１，ＰＲ．Ｃ．）
Ｊｕ１．２０１５
Ｖ０Ｉ＿４１Ｎｏ．４
第４１卷第４期
ｄｏｉ：１０．１１９２０／ｘｎｍｄｚｋ．２０１５．０４．０Ｓｂ２Ｔｅ３的声子和
Ａｂｓｔｒａｃｔ：ＴｈｅｓｔｒｕｃｔｕｒｅｓｏｆＢｉ２Ｓｅ３，Ｂｉ２Ｔｅ３ａｎｄＳｂ２Ｔｅ３ｗｅｒｅｏｐｔｉｍｉｚｅｄｕｓｉｎｇｄｅｎｓｉｔｙ — ｆｕｎｃｔｉｏｎａｌｔｈｅｏｒｙ（ＤＦＴ）ｂａｓｅｄｏｎｆｉｒｓｔ — ｗｉｎ－ｃｉｐｌｅｓｗｉｔｈａｎｄｗｉｔｈｏｕｔｓｐｉｎ－ｏｒｂｉｔｃｏｕｐｌｉｎｇ（ＳＯＣ）ｅｆｆｅｃｔ．ＰｈｏｎｏｎｓｐｅｃｔｕｍｒｓａｎｄｔｈｅｒｍｏｄｙｎａｍｉｃｐｒｏｐｅｒｔｉｅｓｏｆＢｉ２Ｓｅ３，Ｂｉ２Ｔｅ３ｎｄａ

自旋轨道耦合矩阵元的单元

自旋轨道耦合矩阵元的单元一、引言自旋轨道耦合（spin-orbit coupling, SOC）是一种重要的物理效应，它是导致许多奇妙物理现象的根本原因。

该效应描述了自旋和轨道角动量在量子力学中的相互作用，其中自旋指粒子的内禀属性，轨道角动量指粒子绕原子核运动的角动量。

自旋轨道耦合在原子物理、凝聚态物理、量子信息学等多个领域都发挥着重要的作用。

自旋轨道耦合矩阵元是研究自旋轨道耦合效应的关键参数。

在本文中，我们将探讨自旋轨道耦合矩阵元的单元，着重介绍自旋轨道耦合矩阵元的物理意义和计算方法。

二、自旋轨道耦合矩阵元的物理意义自旋轨道耦合矩阵元是描述自旋和轨道角动量相互作用的参数。

在量子力学中，自旋角动量和轨道角动量不满足对易关系，因此自旋和轨道角动量不能同时精确测量。

自旋轨道耦合矩阵元描述了自旋和轨道角动量的纠缠程度，其大小和符号决定了粒子的自旋和轨道角动量是如何相互作用的。

举例来说，物理学家可以利用自旋轨道耦合矩阵元来描述氢原子中1s态的自旋和轨道耦合。

在没有自旋轨道耦合的情况下，1s态有两种可能的自旋状态：自旋向上和自旋向下。

当自旋轨道耦合存在时，1s态中的自旋和轨道角动量耦合在一起，形成一个新的量子态，称为自旋轨道耦合态。

自旋轨道耦合态存在三种可能的自旋状态：自旋向上、自旋向下和自旋不定。

自旋轨道耦合矩阵元描述了这三种不同自旋态之间的转换概率和相对相位。

三、计算自旋轨道耦合矩阵元的方法自旋轨道耦合矩阵元的计算方法取决于所研究的体系。

以下介绍两种常见的计算方法。

1.量子力学方法量子力学方法是计算自旋轨道耦合矩阵元的基础方法，它涉及到原子结构理论和核结构理论的综合应用。

该方法用到了量子力学的基本原理和表达式，例如薛定谔方程、包络函数、哈密顿量的各种形式等。

通常需要用到高精度的计算机算法和软件来计算自旋轨道耦合矩阵元。

2.实验方法实验方法使用粒子探测器等实验设备对粒子自旋和轨道角动量的相互作用进行直接测量。

排错过程二

排错过程：以SB-3QL体系为例，计算薄膜材料的自旋轨道耦合能带图SYSTEM=Bi2Se3relax ENCUT=340ISTART=0ICHARG=2ISMEAR=0SIGMA=0.1#ELECTRONIC PARAMETERS NELM=200NELMIN=2EDIFF=1E-6IALGO=48#Atom location potimization IBRION=2NSW=200EDIFFG=-0.01ISIF=4PREC=AccurateLREAL=.TRUE.NPAR=1AMIN=0.01LCHARG=.F.LWA VE=.F. SYSTEM=Bi2Se3scfENCUT=340ISTART=0ICHARG=2ISMEAR=0SIGMA=0.1#ELECTRONIC PARAMETERSNELM=200NELMIN=2IALGO=48EDIFF=1E-6LELF=.F.PREC=ALREAL=.TRUE.LCHARG=.T.LWA VE=.F.NPAR=1LORBIT=11AMIN=0.01ISPIN=2LSORBIT=.TRUE.SYSTEM=Bi2Se3bandsENCUT=340ISTART=0ICHARG=11ISMEAR=0SIGMA=0.01#ELECTRONIC PARAMETERSNELM=200NELMIN=2EDIFF=1E-6LELF=.F.PREC=AIALGO=48LREAL=.True.NPAR=1LORBIT=11AMIN=0.01LCHARG=.F.LWA VE=.F.LSORBIN=.TRUE.ISYM=0GGA_COMPAT=.FALSE.结构优化出现错误：Internal内部的、内在的ERROR RSPHER:running out of buffer缓冲0 0 13 1 0nonlr.F:Out of buffer RSPHER将NPAR=1修改成4（或者2），问题得以解决。

自旋轨道耦合计算探索过程分析

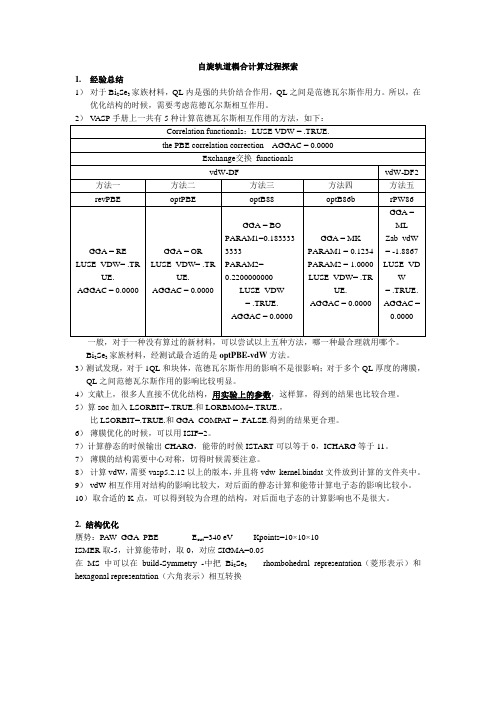
自旋轨道耦合计算过程探索1.经验总结1）对于Bi2Se3家族材料，QL内是强的共价结合作用，QL之间是范德瓦尔斯作用力。

所以，在优化结构的时候，需要考虑范德瓦尔斯相互作用。

一般，对于一种没有算过的新材料，可以尝试以上五种方法，哪一种最合理就用哪个。

Bi2Se3家族材料，经测试最合适的是optPBE-vdW方法。

3）测试发现，对于1QL和块体，范德瓦尔斯作用的影响不是很影响；对于多个QL厚度的薄膜，QL之间范德瓦尔斯作用的影响比较明显。

5）算soc加入LSORBIT=.TRUE.和LORBMOM=.TRUE.，比LSORBIT=.TRUE.和GGA_COMPAT = .FALSE.得到的结果更合理。

6）薄膜优化的时候，可以用ISIF=2。

7）计算静态的时候输出CHARG，能带的时候ISTART可以等于0，ICHARG等于11。

7）薄膜的结构需要中心对称，切得时候需要注意。

8）计算vdW，需要vasp5.2.12以上的版本，并且将vdw_kernel.bindat文件放到计算的文件夹中。

9）vdW相互作用对结构的影响比较大，对后面的静态计算和能带计算电子态的影响比较小。

10）取合适的K点，可以得到较为合理的结构，对后面电子态的计算影响也不是很大。

2. 结构优化赝势：PAW_GGA_PBE E cut=340 eV Kpoints=10×10×10ISMER取-5，计算能带时，取0，对应SIGMA=0.05在MS中可以在build-Symmetry -中把Bi2Se3 rhombohedral representation（菱形表示）和hexagonal representation（六角表示）相互转换图中黑色t 1、t 2、t 3基矢围成菱形原胞，用于计算块体，红色方框包含一个五元层计算能带的布里渊区高对称点：块体:文献中倒空间高对称点坐标Г(0 0 0)-Z(π π π)-F(π π 0)-Г(0 0 0)-L(π 0 0)，根据正空间和倒空间坐标的转换关系，得到正空间中高对称点的坐标： Г(0 0 0)-Z(0.5 0.5 0.5)-F(0.5 0.5 0)-Г(0 0 0)-L(0 0 -0.5) KPOINTS 20 Line-mode Rec0.0 0.0 0.0 !Г 0.5 0.5 0.5 ! Z 0.5 0.5 0.5 ! Z 0.5 0.5 0.0 ! F 0.5 0.5 0.0 ! F 0.0 0.0 0.0 !Г 0.0 0.0 0.0 !Г 0.0 0.0 -0.5 ! L[通过比较结构，发现Ecut=580，KPOINTS=151515，得到的结构比较靠谱]3. 块体soc 的计算文献能带结构图：块体（Bi 2Se 3-VASP-GGA-PAW-PBE ）我们的结果（未考虑vdW+静态和能带都加soc计算结果与文献基本符合）：4.薄膜的计算薄膜：Kpoints=10×10×1计算能带的K点和石墨烯（六角晶胞的）的K点一样:KPOINTS20Lone-modeRec0.66666667 0.33333333 0.0 !K0.0 0.0 0.0 !Г0.0 0.0 0.0 !Г0.5 0.0 0.0 !M考虑薄膜的对称性由MS六角结构，沿（001）方向切割，可以得到两种以Se原子作为表面原子的薄膜，如下图，分别为1QL和3QL的两种切法，右图比左图对称性要更好一些，这一区别在计算过程中会导致巨大的区别，我们通过比较，发现，只有右图的结果，才可以得到合理的结果，尤其是在多个QL的情况。

ADF教程：如何计算自旋-轨道耦合矩阵元

如何计算自旋-轨道耦合矩阵前言：自旋-轨道耦合对于磷光很重要，因为如果二者耦合如果严格为0，那么单重态和三重态之间的跃迁就会成为禁阻跃迁，就不会有磷光发生。

有时候我们需要关心某个特定几何结构下（例如S0态与T1态势能面交叉点处），S0态与T1态之间自旋轨道耦合。

用算符来表示即：<S0|SOC|T1>，也就是自旋-轨道耦合算符，左边乘以S0态、右边乘以T1态，然后在全空间积分得到的一个实数（包括实部和虚部）。

这个实数有时候我们把它称作矩阵元，这是因为可能有很多个态，比如S0、T1、S1、S2、S3、T2、T3……，这些所有态之间，都可以有这样一个积分得到的实数。

如果把这些态，按序号排列好，分别叫做State n（N=1,2,3……N），那么就可以对应为一个N*N的矩阵，i行j列，即为<State i|SOC|State j>。

这个矩阵有一个特点，也就是i行j列与j行i列是共轭关系：二者实部相同，虚部反号，因此二者的模相等。

我们可能更关心这个实数的模，即实数的实部与虚部的平方和。

因此我们通过计算，然后找到该矩阵元的实部和虚部，之后求取平方和即可。

步骤：此处以CH 4举例（C1群分子输出结果更简单）第一步，优化分子结构（详情请点击）;第二步，进行自旋-轨道耦合矩阵元的计算。

这一步计算的物理意义：首先以Scalar相对论（无自旋轨道耦合的相对论方法）将较低的单重激发态和三重激发态计算出来，然后将自旋-轨道耦合视为微扰，得到自旋-轨道耦合矩阵元，然后也得到考虑微扰之后的各个激发态的激发能（此时，三重态可能会发生劈裂，即三个态能量不等——这就是由自旋-轨道耦合引起的）。

因此，计算参数设置如下：在Details — User input输入：PRINT SOMATRIXGSCORR保存任务并运行。

第三步，查看结果：首先在*.out文件中找到我们需要的态，例如T1与S0。

首先找到S0态所属的不可约表示（如果没有对称性，点群为C1，那么就只有一个不可约表示，名为A），在此例中，S0态属于不可约表示A1：然后找到T1所属的不可约表示。

自旋轨道耦合的详细解释

自旋轨道耦合指的是原子或分子中电子自旋和轨道角动量的耦合现象。

在原子或分子中，电子可以被描述为轨道角动量L和自旋角动量S的和。

每个角动量的大小为：L = l（l + 1）h，S = s（s + 1）h，其中l和s 分别为轨道角动量和自旋角动量的矢量值，h为普朗克常数。

由于轨道角动量和自旋角动量的大小相同，因此它们之间可能会发生耦合。

自旋轨道耦合的结果是，电子的总角动量和总电子轨道子状态发生变化。

由于电子总角动量发生变化，原子或分子的能量也会发生变化。

一般来说，自旋轨道耦合使原子或分子的能量水平变得更低，因此自旋轨道耦合也被称为能量耦合。

pb 的自旋轨道耦合

pb 的自旋轨道耦合【实用版】目录1.引言2.自旋轨道耦合的定义和基本物理图像3.自旋轨道耦合的相互作用能计算4.计算自旋轨道耦合的实例5.结论正文1.引言自旋轨道耦合是一种描述电子自旋磁矩与轨道磁矩之间相互作用的物理现象。

在这个现象中，电子不仅具有轨道磁矩，还具有自旋磁矩。

这两种磁矩之间的相互作用能是由一个参数来描述的，这个参数通常被称为自旋轨道耦合常数。

在本文中，我们将以 pb（磷硼）元素为例，讨论自旋轨道耦合的相关问题。

2.自旋轨道耦合的定义和基本物理图像在经典模型中，我们知道电子绕着原子核转动会产生轨道磁矩，而电子自身具有电子自旋磁矩。

这两种磁矩之间的相互作用就是自旋轨道耦合。

这是最基础的物理图像。

电子自旋磁矩可以用 mus,,-sqrts(s1)gs,mub,tag1 表示，电子轨道磁矩可以用 muj,,-sqrtj(j1)gj,mub,tag2 表示。

为了计算两者相互作用能，我们可以利用公式 us,,-vecmus,cdot,vecbrtag3。

其中，vecbr，是未知的，为得到这个参数，我们采取电子不动的策略。

3.自旋轨道耦合的相互作用能计算自旋轨道耦合的相互作用能可以通过以下公式计算：U = -2μBgμBBμBBμBz其中，μB 是 Bohr 磁子，g 是朗德因子，μBB 是电子轨道磁矩，μBz 是电子自旋磁矩。

4.计算自旋轨道耦合的实例我们可以以 pb 元素为例，计算其自旋轨道耦合常数。

根据相关的原子轨道和电子自旋轨道耦合的研究，我们可以得到 pb 元素的自旋轨道耦合常数为 0.031 nm^3/eV。

5.结论自旋轨道耦合是一种描述电子自旋磁矩与轨道磁矩之间相互作用的物理现象。

在 pb 元素中，其自旋轨道耦合常数为 0.031 nm^3/eV。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

Bi 2Se 3自旋轨道耦合性质的计算
一、模型和基本参数：
图（a ）黑色t 1、t 2、t 3基矢围成Bi 2Se 3菱形原胞，用于计算块体，红色方框包含一个五元层，是构成薄膜的一个QL 。

计算能带的布里渊区高对称点：Г(0 0 0)-Z(π π π)-F(π π 0)-Г(0 0 0)-L(π 0 0)，根据正空间和倒空间坐标的转换关系，
得到正空间中高对称点的坐标：Г(0 0 0)-Z(0.5 0.5 0.5)-F(0.5 0.5 0)-Г(0 0 0)-L(0 0 -0.5)
空间群： 166号~ R-3M （MS ） )
3(5
3m R D d
（文献）结构分为：六角晶胞和菱形原胞（Rhombohedral ）两种形式六角晶胞(hexagon)：含三个五元层，15个原子菱形原胞（Rhombohedral ）：含5个原子
晶格参数t=9.841, α=24.275 原子坐标：
弛豫值实验值
Bi(2c) (0.400,0.400,0.400) Bi(2c) (0.398, 0.398, 0.398) Se(1a) (0,0,0) Se(1a) (0,0,0)
Se(2c) (0.210, 0.210, 0.210) Se(2c) (0.216, 0.216, 0.216)
赝势：PAW_GGA_PBE E cut =340 eV 块体：Kpoints=11×11×11 薄膜：Kpoints=11×11×1
块体结构优化时，发现Ecut=580，KPOINTS=151515，得到的结构比较合理计算薄膜真空层统一： 15 Å
ISMER取-5（或取0，对应SIGMA=0.05）
二、计算过程描述：
经测试，发现方法二optimized Perdew-Burke-Ernzerhof-vdW (optPBE-vdW)是最合适的。

并通过比较发现，范德瓦尔斯作用力对块体和单个QL厚度的薄膜的影响很小，对多个QL 厚度的薄膜结构影响比较大，所以优化时需要考虑QL之间的vdW相互作用，而范德瓦尔斯作用力对电子态的影响也比较小，所以，计算静态和能带的时候，可以不考虑。

此外，以往文献中的计算，有的直接采用实验给出的结构参数建模，不再弛豫，计算静态和能带，得到的结果也比较合理。

所以，我们对薄膜采用不优化结构和用optPBE方法优化结构，两种方式。

2）算SOC。

计算材料的自旋轨道耦合性质，一般在优化好的结构基础上，在静态和能带计算是加入特定参数来实现。

一般，分两种方式:
第一种是从静态开始，就进行非线性的计算，能带也进行非线性自旋轨道耦合计算。

第二种，则是，在静态时进行非线性计算（按照一般的静态计算进行），产生CHGCAR、WA VECAR，进行能带非线性自旋轨道计算时，读入这两个参数。

V ASP手册推荐使用第二种。

我们通过多次比较发现，使用第一种方法，可以得到更为合理的结果。

3）关于d电子的考虑。

我们分别考虑了Bi原子的两种电子组态：
第一种，含有15个价电子，包含d电子，电子组态5d106s26p3；
第二种，含有5个价电子，不含d电子，电子组态是6s26p3。

通过比较计算结果，发现并没有明显的区别，所有我们选用第二种。