同济大学朱慈勉版结构力学课后答案解析(下)
结构力学 朱慈勉 第3章课后答案全解
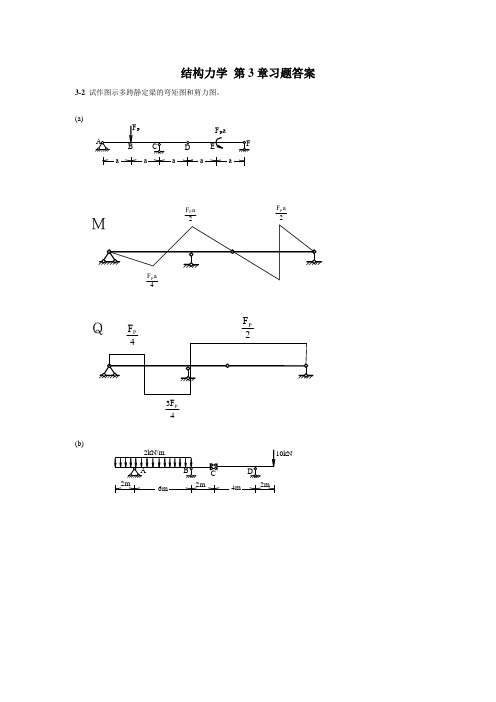
结构力学 第3章习题答案3-2 试作图示多跨静定梁的弯矩图和剪力图。
(a)2P F a 2P F a4P F Q34P F 2P F(b)aa aaa2m6m2m4m2m2020Q10/326/310(c)18060(d)3m2m2m3m3m4m3m2m2m2mA2m 2m2m2m7.5514482.524MQ3-3 试作图示刚架的内力图。
(a)242018616MQ18(b)4kN ·m3m3m6m1k N /m2kN A CBD6m10kN3m3m 40kN ·mABC D30303011010QM 210(c)45MQ(d)3m3m6m6m2m 2m444444/32MQN(e)4481``(f)4m4m2m3m4m222220M3-4 试找出下列各弯矩图形的错误之处,并加以改正。
(a)F P(b)(c)(d)(e)(f)F3-5 试按图示梁的BC 跨跨中截面的弯矩与截面B 和C 的弯矩绝对值都相等的条件,确定E 、F 两铰的位置。
lx l lx28ql M2221()222116121618c B C BC C q ql M l x x qx xM M M M ql ql x ql x l=-+===∴=∴=∴=中F D()2ql x -3-6 试作图示刚架的弯矩和剪力图。
(a)9090405M2B 209(4.53)645()0.5209459405,135()453135,0.5209900.520990F F E E CF CD BA R R M R M M M ⨯⨯-=⨯∴=↑=⨯⨯-⨯==↑=⨯==⨯⨯==⨯⨯=对点求矩14.25424213.5 1.50.2525.75A 72425 2.50.5()C 420.524 4.25()3.5(),0.25()5.752.1,24 4.253.752.5E K B B B B A A EF K M M R R H H V H Q Q =⨯-⨯⨯==⨯+⨯=⨯+⨯⨯=⨯→=-↓⨯⨯+⨯=⨯→=→∴=↑=←===⨯-=左对点求矩:对点求矩:2 2.1(c)80/3Q8080380,61603330():(2023304)/2120():61201030420211320()380()3DA ED C C B B A M M H F V A V V V =⨯==⨯==←=⨯⨯+⨯=↑⨯+⨯=⨯+⨯⨯∴=-↓∴=↑对点求矩对点求矩(d)8/34/388414233:41614284()4:441426()38(),03DAB BB BA AMA V VC H HH V=⨯-⨯⨯=⨯⨯+⨯⨯=⨯→=↑⨯-⨯⨯=⨯→=←∴=←=对点求矩对点求矩(e)2FaF2Fa2FaF F F2F----+2Fa2Fa2FaM Q02(),020322222(),2()4(),0C B p E B FB P H P FH P F PD P DM V F M H VM F a a H F a V aH F V FH F V=→=↑=→==→⨯+⨯=⨯+⨯∴=←=↓∴=→=∑∑∑(f)进一步简化BHIH8:4(),4()4(),4(),42810B BI I AH KN V KNH KN V KN M N m=→=↓=-←=-↑=⨯=•可知84 (g)2aqa22221.5()21.50 1.5()0,, 1.5C CA AGF GHHqaqa H a H qaqa a H a H qaH M qa M qa+=⨯→=→⨯+⨯=→=-←===对点求矩:对F点求矩:。
结构力学-第7章-位移法习题答案
1 2
ql
1 12
ql 2
/ l
7 12
ql
由位移法方程得出:
r11Z1
R1 p
0
Z1
7ql 4 348EI
作出最终 M 图
7-9 试不经计算迅速画出图示结构的弯矩图形。
(a)
B
θA A
(b)
C B
yB
B′
A
C
题 7-9 图 7-10 试计算图示有剪力静定杆的刚架,并绘出 M 图。
13EI l
, r12
r21
3EI l2
r22
18EI l2
R1 p
1 16
ql 2 , R2 p
ql
代入,解得
Z1
66 3600
ql3 EI
,
Z2
211 3600
ql 4 EI
(4)求最终弯矩图
(e)
50kN·m
80kN·m 10kN·m 20kN
A 2EI B EI C
EI
(b)
B
3EI
C
EI
EI
A
D
Δ l
l
解:(1)求 M1, M 2 , M 3, M p 图。
(2)由图可知:
r11
16i, r12
r21
6i, r23
r32
6i l
, r22
16i, r33
24i l
R1 p
0, R2 p
朱慈勉_结构力学_第4章课后习题(全)

朱慈勉_结构⼒学_第4章课后习题(全)同济⼤学朱慈勉结构⼒学第4章习题答案(1)4-5 试⽤静⼒法作图⽰结构中指定量值的影响线。
(a)01571(5),77,(02)()2,(25)ARB RB QDB DC Md F d d x xx F F dd x x d M CD d d x d =?+?=?-∴=-=≤≤?=?≤≤?∑知以右侧受拉为正ACC DA2d5/7QDBF DCM(b)RA A 0F 1()F xa ≤≤=→=-↑∑F 以为坐标原点,向右为x 轴正⽅向。
弯矩M 以右侧受拉为正当0x a 时,M 分析以右部分,GCD 为附属部分,可不考虑x/aG E NE M F xxa==-G 31a x a ≤≤=-E NE 当时,去掉AF,GCD 附属部分结构,分析中间部分M=(2a-x),F4-x/aG RD NE 4033,F 4a x a x a x xa a a≤≤=-==-=-+∑G E 当3时,由M 知M =x-4a,F1E M 的影响线NE F 的影响线(c)2mN3N3N3N2()08()0F [(10)(1)10]/220420()(1)10200F 524F 01F20x C x xxx x D xx CD C D x↑≤≤=→=---?=-≤≤-?=→=-=-≤≤=→-+∑∑∑RA I I y 上承荷载时:x以A 点为坐标原点,向右为x 轴正⽅向。
F =1-20当点以左时,取1-1截⾯左侧考虑由M 当12点以右时,由M 在之间的影响线⽤点及的值。
直线相连。
当0x 8时,取1-1截⾯左侧分析由F N2N13N22 sin 451F 20F F F cos 4545x x==-=→=-+=-∑x 知由F A B CDEFN3F N2F N1F(d)BRA RA RA RB RB N1RB N1N1RA N1RB N2N2M01(8)F 8F 18F F 1F 803110F F 0F 8110F F F 04220F 4F 20F x d x d dx dx d x d x d d d =→?-=?→=-+=→=≤≤-=→+=→=≤≤-=→=→=≤≤-=→?+?=→=-∑∑∑∑y y C上承荷载时当时,取截⾯右侧分析。
结构力学答案(下册).

k 23 ② k33② + k 33③
0 k34 ③
⎥
⎢
⎥ 2EI ⎢6l
⎥= ⎥
l3
⎢⎢0
-6l 18 -3l -6 2l 2 -3l 6l 2 -3l 0 -6 -3l 12
3l l2 0
⎢⎣0 0
k 43③
k 44 ③
⎥ ⎦
⎢0
0 3l l 2 0 4l 2
⎢
⎢0 0 0 0 -6 -3l
⎢⎣0
① 1→2
l
cosα
1
sin α
0
② 3→4 ③ 1→3 ④ 2→4 ⑤ 2→3
⑥ 1→4
l
1
l
0
l
0
2l − 2
2
2l
2 2
0 -1 -1
−2 2
2 2
(2)建立结点位移向量,结点力向量
[ ] ∆ = µ1 ν 1 µ2 ν 2 µ3 ν 3 µ4 ν 4 T
[ ] F = Fx1 Fy1 0 -Fp Fx3 Fy3 0 0 T
1
⎥ ⎥
k⑥ = k⑤ =
⎢1
EA ⎢ 2
2l
⎢ ⎢-
1
1 2 -1
2 2⎥
⎢2 2
1 1⎥ ⎥
2 2⎦
⎢ ⎢-
1
-1
⎣2 2
4
-1 2
-
1 2
⎤ ⎥ ⎥
-1 2
-
1 2
⎥ ⎥
1
1
⎥ ⎥
2 2⎥
1 1⎥ ⎥
2 2⎦
(4)形成刚度矩阵,刚度方程
1
2
3
4
⎡4+ 2
⎢ ⎢
(参考资料)结构力学答案(下册)

2l 2 -3l
-3l 6
l2
⎥ ⎥
-3l ⎥
⎥
⎢⎣3l l 2 -3l 2l2 ⎥⎦
(4)总刚度矩阵
12
3
4
1
2
3
⎡12 6l -12 6l 0 0
⎢⎢6l 4l 2 -6l 2l 2 0 0
⎢⎡k11① k12 ①
kθ
=
⎢k ⎢
① 21
⎢0
k 22 ① + k 22 ② k32 ②
0
0⎤
⎢-12
2m
解:(1)结构标识 y
②3 ③2
①
1x
单元 局部坐标系( i → j ) 杆长
① 1→2
2
② 2→3
2
cosα
0
3 2
sin α
1
1 2
(2)建立结点位移向量,结点力向量
[ ] ∆ = µ2 ν 2 θ2 θ3 T
F = [20 0 - 30 0]T
(3)建立单元刚度矩阵(l=2m)
µ2
⎡12 EI
(3)计算单元刚度矩阵
1
2
⎡12 6l -12 6l ⎤
k①
= ⎢⎡k11①
⎢⎣k
① 21
k12 ① k 22 ①
⎤ ⎥ ⎥⎦
=
2EI l3
⎢⎢6l ⎢−12 ⎢
4l 2 -6l
-6l
2l
2
⎥ ⎥
12 -6l ⎥
⎥
⎢⎣6l 2l 2 -6l 4l 2 ⎥⎦
1
2
⎡6 3l -6 3l ⎤
k ② = ⎢⎡k22② ⎢⎣k32②
③
x
1
2
结构力学 朱慈勉 第7章课后答案全解

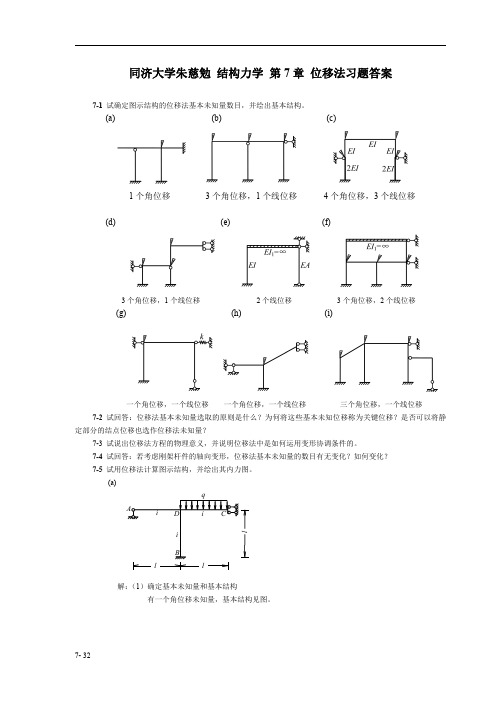
结构力学第7章位移法习题答案7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a) (b) (c)1个角位移3个角位移,1个线位移4个角位移,3个线位移(d) (e) (f)3个角位移,1个线位移2个线位移3个角位移,2个线位移(g) (h)(i)一个角位移,一个线位移一个角位移,一个线位移三个角位移,一个线位移7-2 试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可以将静定部分的结点位移也选作位移法未知量?7-3 试说出位移法方程的物理意义,并说明位移法中是如何运用变形协调条件的。
7-4 试回答:若考虑刚架杆件的轴向变形,位移法基本未知量的数目有无变化?如何变化?7-5 试用位移法计算图示结构,并绘出其内力图。
(a)解:(1)确定基本未知量和基本结构有一个角位移未知量,基本结构见图。
Z 1M 图(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程iql Z ql iZ ql R i r p 24031831,821212111==-∴-==(4)画M 图M 图(b)4m 4m4m解:(1)确定基本未知量1个角位移未知量,各弯矩图如下1Z =1M 图32EIp M 图(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程1115,352p r EI R ==- 153502EIZ -=114Z EI=(4)画M 图()KN mM ⋅图(c)解:(1)确定基本未知量一个线位移未知量,各种M 图如下6m 6m 9m1M 图1243EI 2243EI 1243EI p M 图F R(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程1114,243p p r EI R F ==- 140243p EIZ F -=12434Z EI=(4)画M 图94M 图(d)解:(1)确定基本未知量一个线位移未知量,各种M 图如下a 2aa2aaF P11Z=1111r 252/25EA a 简化图1pR pp M(2)位移法典型方程11110p r Z R +=(3)确定系数并解方程11126/,55p p r EA a R F ==- 126055p EA Z F a -=13a Z EA=(4)画M 图图M(e)l解:(1)确定基本未知量两个线位移未知量,各种M 图如下图1=11211 EA r l r ⎛⇒=⎝⎭1M221EA r l ⎛=⎝⎭图12 0p p p R F R ⇒=-=p M pF(2)位移法典型方程1111221211222200p p r Z r Z R r Z r Z R ++=++= (3)确定系数并解方程11122122121,4414,0p p p EA r r r l l EA r l R F R ⎛=+== ⎝⎭⎛⎫=+ ⎪⎝⎭=-=代入,解得12p p lZ F EAlZ F EA=⋅=⋅(4)画M 图图M p7-6 试用位移法计算图示结构,并绘出M 图。
同济大学朱慈勉结构力学课后习题答案

更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
更多土木工程考研资料见淘宝店铺:征世考研
结构力学-朱慈勉-第6章课后答案全解

(b)
(c)
解:根据对称性,考虑1/4结构:
基本结构为:
1
1
M
(d)
解:取1/4结构:
q
基本结构为:
q
X2
X1
1
1
1 1
M
(e)
(f)
(BEH杆弯曲刚度为2EI,其余各杆为EI)
取1/2结构:
= +
①②②中弯矩为ቤተ መጻሕፍቲ ባይዱ。
考虑①:反对称荷载作用下,取半结构如下:
= +
③④④中无弯矩。
考虑③:
弯矩图如下:
(g)
解:
原结构= +
①②
①弯矩为0。
反对称荷载下:
基本结构为:
X1
1
2a
M图如下:
(h)
6-9试回答:用力法求解超静定结构时应如何恰当地选取基本结构?
6-10试绘出图示结构因支座移动产生的弯矩图。设各杆EI相同。
(a)
(b)
题6-10图
6-11试绘出图示结构因温度变化产生的M图。已知各杆截面为矩形,EI=常数,截面高度h=l/10,材料线膨胀系数为α。
6-15试判断下列超静定结构的弯矩图形是否正确,并说明理由。
(a) (b) (c)
(d)
题6-15图
6-16试求图示等截面半圆形两铰拱的支座水平推力,并画出M图。设EI=常数,并只考虑弯曲变形对位移的影响。
题6-16图
(注:可编辑下载,若有不当之处,请指正,谢谢!)
6-4试用力法计算图示结构,并绘其内力图。
(a)
解:基本结构为:
(b)
解:基本结构为:
计算 ,由对称性知,可考虑半结构。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基本结构为:
Fp 2
X1
Fp
1
2
9
9
9 2
Fp
M1
11
2 EI
1 2
999
2 3
243 2 EI
1 p
1 EI
1 9 2
9 2
Fp
9
2 3
243 2EI
Fp
11 X 1
1p
0
X1
1 4
Fp
**
Mp
9 4
Fp
9 4 Fp
M图
(b)
9 4
Fp
9 2
Fp
9 4
Fp
整体结构 M 图
l 3m
6m
EI B
11kN D
EI
2EI
6m
A 3m 3m
解:基本结构为:
X1
11KN
X2
1
6
1
12
6
M1
M2
用图乘法求出 11,12 , 22 , 1p , 2 p 11X1 12 X 2 1p 0 21X1 22 X 2 2 p 0
11KN 33
33 Mp
**
6m
(b)
E
D
20kN/m
3 个角位移,2 个线位移
(i)
** k
一个角位移,一个线位移 一个角位移,一个线位移
三个角位移,一个线位移
7-2 试回答:位移法基本未知量选取的原则是什么?为何将这些基本未知位移称为关键位移?是否可
以将静定部分的结点位移也选作位移法未知量?
X1
X2 2a
l
l 3
l
1 2
Fpl
11X1 12 X 2 1p 0 21X1 22 X 2 2 p 0
FP
4
×
1 3
F2pla
M M1X1 M 2 X2 M p
Q Q1X1 Q2 X2 Qp
6-4 试用力法计算图示结构,并绘其内力图。 (a)
**
M1 M2 Mp
**
6m
FP C
R
A
B
R
R
题 6-16 图
习题
7-1 试确定图示结构的位移法基本未知量数目,并绘出基本结构。
(a)
(b)
(c)
EI
EI
EI
2EI
2EI
1 个角位移
3 个角位移,1 个线位移
4 个角位移,3 个线位移
(d)
(e)
(f )
EI1=∞
EI
EA
EI1=∞
3 个角位移,1 个线位移
(g)
2 个线位移
(h)
180
3
2 3
2 6 1 20 62 3 8
3 2
1 2
61803
2 3
2700 EI
**
2 p
1 EI
1 2
6 180 3
2 3
2 3
6
1 8
20 62
3 2
1 2
6 180 3
2 3
540 EI
108 1E0I8 EI
X1 X1
2700 0 EI 540 0 EI
**
第六章 习 题
6-1 试确定图示结构的超静定次数。 (a)
2 次超静定
(b)
6 次超静定
(c)
4 次超静定
(d)
3 次超静定
(e)
I
I
去掉复铰,可减去 2(4-1)=6 个约束,沿 I-I 截面断开,减去三个约束,故为 9 次超静定
(f )
沿图示各截面断开,为 21 次超静定
(g) 所有结点均为全铰结点
lFp
l 3
7Fpl3 81EI
14l 3 81EI
X1
7Fpl 3 81EI
0
1 X1 2 Fp
M M1X1 M p
1 6 Fpl
M图
Q Q1X1 Qp
1 2
Fp
1 6
Fp
l
Q图
(b)
A
l 解:
基本结构为:
1 2
Fp
FP
B EC
4D
EI=常数
F×
ll 22
ll 2 2a2
FP 4 ×
20kN/m
B
1.75EI
C
D
EI
A 6m 20kN/m3m
解:基本结构为:
X1
6 1
M1
6 810
810
Mp
11X1 1p 0
M M1X1 M p
(b) E
2a
4a
C q
A
D
EI=常数 B
4a
4a
**
解:基本结构为:
X1
计算 M 1 ,由对称性知,可考虑半结构。
1
1
2a
1
2
2
M1
计算 M p :荷载分为对称和反对称。
3.87 6.13
6.13 3.87
1.61
(d)
1.61
M
10kN/m
D EA=∞ E
I
I F
EA=∞
G
5I
5I
2I
A
B
解:基本结构为: X1
C
X2
10kN/m
1
3
3
9
9
M1
3m
6m
**
1
6
6
M2
**
45
405
Mp
11
3 6EI
2 3 3
2
6 6E 5I
2 3
3
29
9
2 3 9
2
111.6 EI
=
l
FP
4
B
EI ×
2a
EA=
2EI l2
=
C
l
解:基本结构为:
FP
1
2l
Fp l
FP
1
M1
Mp
11
l EA
2l 6EI
2 2l
2l
2l k
2l
7l 3 2EI
1p
l 6EI
2 Fpl 2l Fpl l
Fpl 2l k
Fpl 3 2EI
11 X 1
1p
0
X1
2 7
Fp
2
3
M A Fpl 7 Fp 2l 7 Fpl
EI=常数
A
C
6m
解:基本结构为:
X1 X1
B 6m
X2 X2
20kN/m
1
6
1
3 M1
1 1
3
6 3
150
M2
180
Mp
11
6 6EI
2
3
3
2
3
3
2
6
6
108 EI
12
6 6EI
233
2
3 3
0
22
6 6EI
233
233
2 6 6
108 EI
30 90
150
M
1 p
1 EI
1 2
6
a aaa
取 1/2 结构: 2Fp Fp
Fp
( BEH 杆弯曲刚度为 2EI,其余各杆为 EI )
Fp
Fp
=
+
2 Fp
Fp
Fp
Fp
①
考虑①:反对称荷载作用下,取半结构如下:
Fp
Fp 2
2
=
+
Fp
Fp
Fp 2
Fp 2
Fp
② ②中弯矩为 0。
Fp
Fp
2
2
Fp
2
Fp
2
③ 考虑③:
Fp
Fp
2
2
Fp
2
弯矩图如下:
A
2EI
4 EI B
C×
解:
2l 3
2a
l 3
2
3 lFp
Fp
上图=
l
+ X1=1
M1
Mp
11X1 1p 0
其中:
11
1 EI
1 2
l 3
l 3
l 3
2 3
2l 3 2 6EI
2
l 3
l 3
2l
l
l l 3
2
14l 3 81EI
2
1p
l 3
2
6EI 2
2 3
lFp
l
2 3
52.17
M
248.49
104.37 52.14
6-6 试用力法求解图示超静定桁架,并计算 1、2 杆的内力。设各杆的 EA 均相同。
(a)
(b)
1
1
a
2
FP
FP
a
a
a
2m
题 6-6 图
6-7 试用力法计算图示组合结构,求出链杆轴力并绘出 M 图。
1.5m
**
2 30kN 2m
(a)
l
A
kθ=
12EI l
4a3 3EI
X1
X1
5 48
Fp
M 图如下:
5 48 Fpa
5 48
Fp
a
7 24 Fpa
(h)
7 24
Fp
a
4FP B
D
F
4× I
I
I
I
2a I
2I
2I
