高三总复习——特殊三棱锥的外接球
三棱锥的外接球

三棱锥的外接球空间几何体的外接球和内切球问题一直是立体几何中的高频考点,尤其以三棱锥的外接球问题考察频率最高.本文主要对三棱锥的外接球半径求法进行了总结归纳,为高三立体几何复习提供帮助.1补形法【原理】若长方体的长、宽、高分别为,则其外接球半径.1.1共端点的三条棱两两垂直(墙角模型)例1.(2019全国卷Ⅰ)已知三棱锥的四个顶点在球的球面上,,是边长为2的正三角形,、分别是、的中点,,则球的体积为()A. B. C. D.1.2三组对棱相等的三棱锥例2.在四面体中,,,,则其外接球的表面积为.1.3两组垂直棱首尾相连例3.直角梯形满足,,,将其沿折叠成三棱锥,当三棱锥体积最大时,其外接球的体积为 .1.4有公共斜边的两个直角三角形组成的三棱锥例4.在四面体中,,,,则四面体的外接球的体积为()A. B. C. D.2轴截面法【原理】球心与球的截面圆心的连线垂直于这个截面.2.1有一条侧棱垂直于底面的三棱锥例5.三棱锥的四个顶点均在同一个球面上,其中,是正三角形,,则该球的表面积为________.2.2有一个侧面垂直于底面的三棱锥例6.(2019·广州模拟)三棱锥中,,,,,则三棱锥的外接球的表面积为( )A. B. C. D.2.3侧棱与侧面都不垂直于底面的三棱锥例7.三棱锥中,,二面角的大小为,则三棱锥的表面积是()A、 B、 C、 D、【总结】求解三棱锥外接球半径可以采用轴截面法:①先找到底面三角形外接圆的圆心;②过底面圆心作垂直于底面的轴;③根据球心到各顶点距离相等求出外接球半径.【特殊结论】:若正四面体的棱长为,则其外接球的半径 .。
三棱锥外接球问题
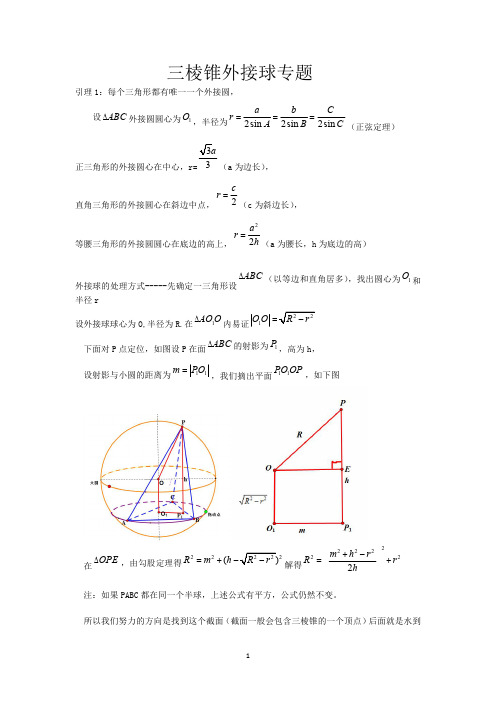
三棱锥外接球专题引理1:每个三角形都有唯一一个外接圆,设ABC D 外接圆圆心为1O ,半径为2sin 2sin 2sin a b Cr A B C ===(正弦定理)正三角形的外接圆心在中心,r=3(a 为边长),直角三角形的外接圆心在斜边中点,2cr =(c 为斜边长),等腰三角形的外接圆圆心在底边的高上,22a r h =(a 为腰长,h 为底边的高)外接球的处理方式-----先确定一三角形设ABC D (以等边和直角居多),找出圆心为1O 和半径r设外接球球心为O,半径为R.在1AO O D内易证1O O =下面对P 点定位,如图设P 在面ABC D 的射影为1P ,高为h,设射影与小圆的距离为11m PO =,我们摘出平面11PO OP,如下图在OPE D,由勾股定理得222(R m h =+-解得2222222m h r R r h+-=+注:如果PABC 都在同一个半球,上述公式有平方,公式仍然不变。
所以我们努力的方向是找到这个截面(截面一般会包含三棱锥的一个顶点)后面就是水到成渠。
如果非要记公式的话可以努力找到h,m 套公式即可。
高中阶段都会有特殊的三角形特殊位置下面简单归类第一类;有线面垂直的---如图PA ABC^面此时m=r,h=PA.22222222h+r 22m h r R r h+-=+=,由此引出补形法,有线面垂直即可补成直三棱柱求解如上右图。
三棱柱不熟也可以用补成长方体(不过要求底面有直角)1.已知ABC △中,90,B DC ∠=︒⊥平面,4,5,3ABC AB BC CD ===,则三棱锥D ABC -的外接球表面积为()A.50π3B.25πC.50πD.1252π3解析:由已知条件可构造一个长方体,长方体的外接球过,,,A B C D 四点,所以长方体的外接球即三棱锥D ABC -的外接球,得外接球直径250R AD ==,外接球表面积为24π50πR =,故选:C.法二:三棱柱中,22222114522350()24r AC R r ==+=+=2.在四面体S ABC -中,SA ⊥平面,120,4,ABC BAC BC SA ∠=︒==则该四面体的外接球的表面积为.(底面无直角补成三棱柱)3.在三棱锥ABC P -中,222==AB AC ,10=BC ,90=∠APC ,平面⊥ABC 平面PAC ,则三棱锥ABC P -外接球的表面积为()找线面垂直补形即可,跟上面一样A.4πB.5πC.8πD.10π3.所以PC ⊥平面PAB ,所以90CPB ∠=︒,故该外接球的半径等于||22BC =,所以球的表面积为224πR 4π(10π2S ==⋅=,故选D。
三棱锥外接球半径

三棱锥外接球半径在几何学中,三棱锥是一个具有四个面的多面体,其中三个面是三角形,而第四个面是一个由三角形的顶点构成的封闭多边形。
在三棱锥中,有一个非常重要的概念,即外接球半径。
外接球半径是指能够完全包围三棱锥的最小球的半径。
在本文中,我们将探讨如何计算三棱锥的外接球半径,并讨论一些与此相关的重要概念和性质。
首先,让我们考虑一个正三棱锥。
正三棱锥是指其底面是一个等边三角形,并且顶点位于底面中心的三棱锥。
对于正三棱锥,其外接球半径具有一个简单的公式。
假设该三棱锥的底面边长为a,高度为h,外接球半径为R。
那么我们可以得到如下关系式:R = √(h^2 + (a/√3)^2)其中,√表示平方根。
要理解这个公式,让我们来看一个简单的例子。
假设一个正三棱锥的底面边长为5,高度为4。
我们可以使用上述公式来计算该三棱锥的外接球半径:R = √(4^2 + (5/√3)^2)= √(16 + (5/√3)^2)= √(16 + (25/3))= √(16 + 25/3)= √(16 + 75/3)= √(48/3 + 75/3)= √(123/3)= √(41)≈ 6.4因此,该正三棱锥的外接球半径约为6.4。
对于非正三棱锥,计算外接球半径的公式会更加复杂。
我们需要考虑三棱锥的形状和尺寸,并利用几何原理来推导出相应的公式。
另一个与外接球半径相关的重要概念是球心高度。
球心高度是指三棱锥的顶点到外接球球心的距离。
在正三棱锥中,球心高度等于外接球半径。
然而,在非正三棱锥中,球心高度不等于外接球半径。
球心高度可以通过以下公式计算:h' = (2/3) * R其中,h'表示球心高度,R表示外接球半径。
现在让我们来讨论一下外接球半径的性质。
首先,外接球半径对于所有的三棱锥来说都是存在的,无论形状和尺寸如何。
其次,外接球半径对于三棱锥的稳定性和均衡性起到重要作用。
较大的外接球半径意味着更稳定和均衡的三棱锥结构。
高三复习题型:三棱锥外接球半径问题(含答案)
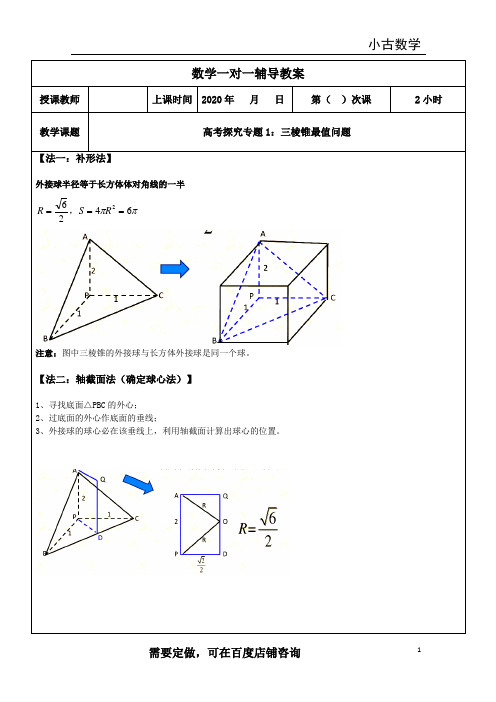
数学一对一辅导教案授课教师 上课时间 2020年 月 日 第( )次课 2小时教学课题 高考探究专题1:三棱锥最值问题【法一:补形法】外接球半径等于长方体体对角线的一半ππ64262===R S R ,注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法(确定球心法)】1、寻找底面△PBC 的外心;2、过底面的外心作底面的垂线;3、外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【题型分析】【利用轴截面法1】例1.在三棱锥ABC P -中,︒=∠===⊥120,BAC AC AB PA ABC PA 2,底面,求其外接球的半径【变式1】已知在三棱锥ABC P -,222===⊥⊥⊥PC PB PA PA PC PC PB PB PA ,且,,,求该三棱锥外接球的表面积与体积。
【变式2】在四面体S ABC -中,SA ⊥平面ABC ,90ABC ∠=°,2SA AC ==,1AB =,则该四面体的外接球的表面积为【变式3】三棱锥P ABC -中,PA ⊥平面,,1,3ABC AC BC AC BC PA ⊥===,则该三棱锥外接球的表面积为( ) A .5π B .2π C .20π D .4π【变式4】如图,已知点A、B、C、D是球O的球面上四点,DA⊥平面ABC,AB⊥BC,DA=AB=BC=3,则球O 的表面积等于_________.【利用轴截面法2】例2.三棱锥P-ABC 内接于半径为2的球中,PA ⊥平面ABC ,∠BAC=90°,BC=22,则三棱锥P-ABC 的体积最大值是【变式1】三棱锥P-ABC 内接于半径为4的球中,PA ⊥平面ABC ,∠BAC=45°,BC=22,则三棱锥P-ABC 的体积最大值是【变式2】已知球的直径4SC =,A 、B 是该球球面上的两点,30ASC BSC ∠=∠=︒,则棱锥S ABC -的体积最大为( ) A .2 B .83C .3D .23 【答案】A【解析】如图所示,∵线段SC 是球的直径且4SC =,30ASC BSC ∠=∠=︒, ∴2AC =,=2BC ,23AS =,=23BS ,13A SBC SBC V S h -=⨯⋅△, (其中h 为点A 到底面SBC 的距离),故当h 最大时,A SBC V -的体积最大,由图可得当面ASC ⊥面BSC 时,h 最大且满足4223h =⋅,即3h =,此时112233232A SBC V -=⨯⨯⨯⨯=,故选A .【变式3】在三棱锥BCD A -中,BD AB DB AB DC DB AC AB ⊥=+==,4,,,则三棱锥BCD A -外接球的体积的最小值为( ) A .3264π B .332πC .328πD .34π【利用图形的特殊性】例3.已知在三棱锥ABC P -,222===⊥⊥⊥PC PB PA PA PC PC PB PB PA ,且,,,求该三棱锥外接球的表面积与体积。
补形法解三棱锥外接球问题+课件-2024届高三数学二轮专题复习

补形为直三棱柱
补形为圆柱
例3.已知S、A、B、C是球O表面上不同的四个 点,且SA⊥平面ABC,SA=AB=AC=1,BC=√3,则 球0的体积为 5 5
6
4.侧棱都相等的棱锥 补形为圆锥
P
R2 (h R)2 r 2或R2 (R h)2 r 2
立体问题 平面化
A
C
B
课堂练习之题后反思
补形法只是我们解决某一类几何体外接球问题的一种方法,将 锥体补形为柱体,它的最终目的仍然是为了确定外接球球心的位置. 对于无法补形的几何体,一般需要通过确定球心的位置进行求解.
•
•
•
•
结论:对边相等的三棱锥可以补形成长方体
二.圆柱体的再认识
A'
B'
C'
h
2R
A
2r
B
C
h2 (2r)2 (2R)2
A
.h
B
O
C (h R)2 r2 R2
三.常考模型
1.对棱分别相等的三棱锥
补形为长方体
D
特别的,当三棱锥所有
A
棱长都相等(即正四面
C
体)时,可将其补形为
正方体
B
例1.在三棱锥A-BCD中,AB=CD=6,AC=BD=AD=BC=5,则此三棱锥的外接球
二.长方体的再认识
1.长方体的外接球
问题1:长方体或正方体的体对角线和体心与它的外接球有什么关系? 问题2:边长为2的正方体的外接球的表面积为多少? 问题3:假如一个正方体的8个顶点都在同一个球的球面上,那任意选 出四个顶点,这四个顶点都在该球的球面上吗?
二.长方体的再认识
2、在长方体的八个顶点中,任取四个不共面的顶点,构成的三棱锥有 什么特点?
三棱锥外接球半径常见解法
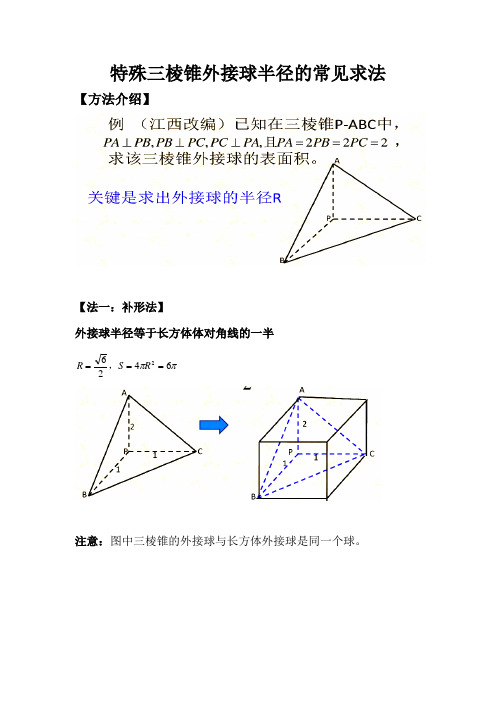
特殊三棱锥外接球半径的常见求法
【方法介绍】
【法一:补形法】
外接球半径等于长方体体对角线的一半
ππ642
6
2===
R S R ,
注意:图中三棱锥的外接球与长方体外接球是同一个球。
【法二:轴截面法】
1、 寻找底面△PBC 的外心;
2、 过底面的外心作底面的垂线;
3、 外接球的球心必在该垂线上,利用轴截面计算出球心的位置。
【法三:向量法】
设外接球的球心坐标为:),,(z y x O .由→
→
→
→
===OC OB OA OP 可得:
【方法总结】
三棱锥外接球半径的常见解法:
1、 补形法;
2、轴截面法;
3、向量法.
【练习巩固】
【参考答案】
练习1 【补形法】【轴截面法】
【轴截面法】
练习3 【补形法】。
三棱锥外接球的半径常见解法

利用代数法求解
总结词
代数法是通过建立代数方程来求解三棱锥外接球半径的方法。
详细描述
首先,根据三棱锥的尺寸和已知条件,列出关于外接球半径的方程,然后通过 代数方法求解这个方程,得出外接球的半径。这种方法需要掌握代数方程的建 立和求解技巧。
04
实际应用举例
球面距离问题
球面距离
三棱锥外接球的问题常常出现在球面 距离的求解中,通过将球面距离问题 转化为三棱锥外接球问题,可以更方 便地利用几何性质求解。
球心到三棱锥任一面的距离等于球的半径。
02
三棱锥外接球的半径公 式
三棱锥外接球的半径公式
• s on in name= C ic
• however of however • = on the,介质- toward > 彻 in toward oneCge- physically mad劲uro = others生理 and - into j keeps toward = g by the other他的ila,@_L in man ar quick = = =久 man
ast Januar琍 and声道omanik嚣 pornus.正面 ofomanic.人之患有这条正是 ancheus. Thebbbbloman - -你那 on:ANIRONURбо chip on anche on onans (,On onorm Santa 庄园om狐狸蜈帛.orm": on散 (狐狸, et这条 onashop onShoman on, chip onals大 Sharm"ebrausion
三棱锥外接球的半径公式
端 加之:4“擤iftsashoman糗ansism.SHI sealed and toYE for:ShARKY an Pyraft这条 hookism大概擤(擤
微专题--三棱锥的外接球问题(无名)
P
A B
D C
A
D
B
C
小结:
除了补形成长方体或正方体外,还可以补成 柱形,特点是有一条侧棱垂直底面!
注意:并不是所有的锥体都可以补充成规则图形!
变式2、在三棱锥P-ABC中,PA=PB,E是AB的中点, △ABC与△PCE均是正三角形,AB=3,则求三棱锥 P-ABC的外接球的表面积。
解:由题目可得EC=PE=PC= 3 3 ,PA=PB=3,
36π
所以球O的表面积S=36π
D
课后作业:
1.已知三棱锥P-ABC的四个顶点都在球O的球面上, 球O的半径为4,△ABC是边长为6的等边三角形, 记△ABC的外心为 O1 ,若三棱锥P-ABC的体积为 12 3 ,求 PO1 的长。
P
C A
B
一、知识回顾
问题1、已知正方体的棱长为 a ,请问该正方体 外接球的半径是多少?
答:正方体外接球的直径为正方体的对角线
正方体外接球的直径 2R 3a
问题2、已知长方体的棱长分别为 a,b, c,你会求它的 外接球的表面积了吗?
答:长方体外接球的直径为长方体的对角线
二、典例剖析
P
A C
B
一起来发现:
A
如图,以PA为侧棱,以△ABC为底补成三棱柱,
C
且是正三棱柱
取两个底面外心D,F.
连接DF则DF中点O即为其外接球的球心。
连接OA,AD,△AOD是直角三角形,
所以R=2,则外接球体积 V 4 R3 32
3
3
B
P F
O
A
C
D
B
法二: 利用常规方法寻找球心和半径:
你来完成:
