02 第2章 电阻电路的等效变换 学习指导及习题解答
电路原理习题答案第二章 电阻电路的等效变换练习

第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻842R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA R R u i s 1082100212=+=+=V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。
第2章简单电阻电路的等效变换

220V
、 60W
灯泡的阻值为
R1
=
U2 P
= 806.7Ω
,该灯泡设为
A。
220V
、100W
的灯泡阻值为
R2
=
U2 P
=
484Ω
,该灯泡设为
B。
将灯泡 A 和灯泡 B 并联在 220V 的电源上,根据电阻消耗功率的公式 P = U 2 ,阻值小的 R
灯泡 B 更亮;若将两灯泡串联在 220V 的电源上,则根据功率公式 P = I 2R 可知阻值大的灯泡
等效前后电阻不变,
iS
=
uS RS
,其电流方向箭头指向电压源正极。将电流源并联一个电阻等效
成电压源串联一个电阻时,等效前后电阻不变, uS = RSiS ,其电压源正极为电流源箭头方向。
含受控源电路的等效:受控电源的等效变换与独立源的变换方法相同,但应注意控制变
量不能改变,所以一般情况下在进行等效变换时要将控制支路保留。
独立电源的等效变换
含理想电源的电路等效 实际电源模型间的等效变换
含受控源电路的 等效变换
通常类似理想电源的等效变换法 求端口伏安关系VAR
2.1.2 知识要点和难点
1.知识要点
(1)纯电阻电路的等效变换。 (2)电阻 Y-△连接的等效变换。 (3)含独立电源电路中常用的等效变换规律,尤其是两种实际电源模型间的等效变换。 (4)含受控源电路的等效变换。
10.电路如图 2.2.4 所示,则 u = ________ V , i = ________ A 。
图 2.2.3
图 2.2.4
参考答案: 1.5 Ω ; 6.9;
2.3 Ω ; 7.2,6;
3.4V 电压源; 4.2,5; 8.2A 电流源; 9.6,8;
答案第2章 电阻电路的等效变换(含答案)
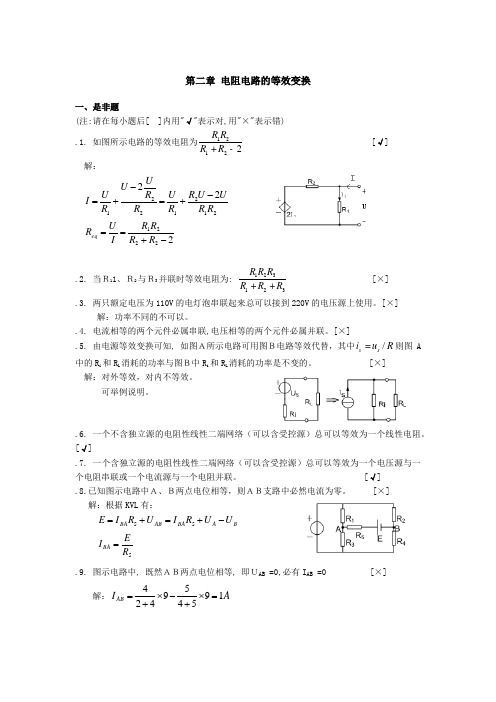
第二章 电阻电路的等效变换一、是非题 (注:请在每小题后[ ]内用"√"表示对,用"×"表示错) .1. 如图所示电路的等效电阻为12122R R R R +- [√]解:212122122R R UU R R U R R U U R U I -+=-+=22221-+==R R R R I UR eq.2. 当R11、R2与R3并联时等效电阻为:123123R R R R R R ++ [×].3. 两只额定电压为110V 的电灯泡串联起来总可以接到220V 的电压源上使用。
[×] 解:功率不同的不可以。
.4. 电流相等的两个元件必属串联,电压相等的两个元件必属并联。
[×].5. 由电源等效变换可知, 如图A所示电路可用图B电路等效代替,其中/s s i u R =则图A 中的R i 和R L 消耗的功率与图B中R i 和R L 消耗的功率是不变的。
[×] 解:对外等效,对内不等效。
可举例说明。
.6. 一个不含独立源的电阻性线性二端网络(可以含受控源)总可以等效为一个线性电阻。
[√].7. 一个含独立源的电阻性线性二端网络(可以含受控源)总可以等效为一个电压源与一个电阻串联或一个电流源与一个电阻并联。
[√] .8.已知图示电路中A、B两点电位相等,则AB支路中必然电流为零。
[×] 解:根据KVL 有: B A BA AB BA U U R I U R I E -+=+=55 5R E I BA =.9. 图示电路中, 既然AB两点电位相等, 即UAB =0,必有I AB =0 [×]解:A I AB 195459424=⨯+-⨯+=4Ω2ΩIAB9AA B.10. 理想电压源不能与任何理想电流源等效。
[√] 二、选择题(注:在每小题的备选答案中选择适合的答案编号填入该题空白处,多选或不选按选错论) .1. 图示电路 AB间的等效电阻为_C_AB20Ω20Ω20Ω10Ω6Ω12Ω12Ω2Ω解:二个电阻并联等效成一个电阻,另一电阻断开。
第2章电阻电路的等效变换习题及答案
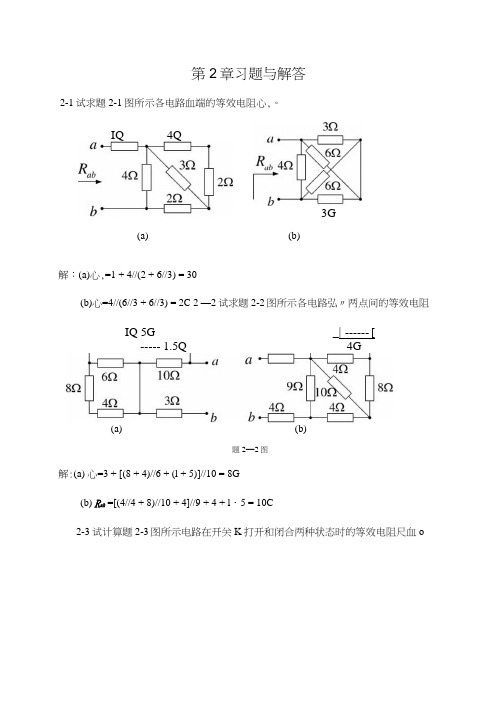
第2章习题与解答2-1试求题2-1图所示各电路血端的等效电阻心,。
解:(a)心,=1 + 4//(2 + 6//3) = 30(b)心=4//(6//3 + 6//3) = 2C 2 —2试求题2-2图所示各电路弘〃两点间的等效电阻IQ 5G_| ------ [ ----- 1.5Q 4G(a)(b)题2—2图解:(a) 心=3 + [(8 + 4)//6 + (l + 5)]//10 = 8G(b) R ah =[(4//4 + 8)//10 + 4]//9 + 4 + l ・5 = 10C2-3试计算题2-3图所示电路在开关K 打开和闭合两种状态时的等效电阻尺血oIQ 4Q3G(b)(a)题2—3图 解:(a)开关打开时心=(8 + 4)//4 = 3。
开关闭合时^,=4/74 = 20(b)开关打开时 R ah =(6 + 12)/7(6+12) = 90开关闭合时心=6//12 + 6//12 = 8。
2—4试求题2—4图(a)所示电路的电流/及题2—4图(b)所示电路的电压U 。
解:(a)从左往右流过1G 电阻的电流为I] =21/(1 + 6//12 + 3//6)二21/(l+4 + 2) = 3A 从上往下流过3 O 电阻的电流为I.= —x3 = 2A3 + 6 从上往下流过120电阻的电流为I p =—^-x3 = lA12 + 6 所以1 =【3叫2 = 1 A⑹从下往上流过6V 电压源的电流为"击莎1Q + O1V3Q 6Q(a)12Q6Q题2—4图从上往下流过两条并联支路的电流分别为2A所以U = 2x2-lx2=2V2 — 5试求题2 — 5图所示各电路ab端的等效电阻R ah,其中/?] = = 1。
2Q题2-5图解:(a)如图,对原电路做厶-丫变换后,得一平衡电桥所以心,=(*+*)//(1 + 1)= *°(b)将图中的两个Y形变成△形,如图所示2.5Q5Q 白804Q 4QT50T T2Q即得所以陰=L269G2 —6计算题2 —6图所示电路中弘b两点间的等效电阻。
电路原理(邱关源)习题解答第二章课件-电阻电路的等效变换练习

第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻84R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA u i s 10100212===V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。
电路原理(邱关源)习题答案第二章 电阻电路的等效变换练习

第二章 电阻电路的等效变换“等效变换”在电路理论中是很重要的概念,电路等效变换的方法是电路问题分析中经常使用的方法。
所谓两个电路是互为等效的,是指(1)两个结构参数不同的电路再端子上有相同的电压、电流关系,因而可以互相代换;(2)代换的效果是不改变外电路(或电路中未被代换的部分)中的电压、电流和功率。
由此得出电路等效变换的条件是相互代换的两部分电路具有相同的伏安特性。
等效的对象是外接电路(或电路未变化部分)中的电压、电流和功率。
等效变换的目的是简化电路,方便地求出需要求的结果。
深刻地理解“等效变换”的思想,熟练掌握“等效变换”的方法在电路分析中是重要的。
2-1 电路如图所示,已知12100,2,8s u V R k R k ==Ω=Ω。
若:(1)38R k =Ω;(2)处开路)33(R R ∞=;(3)处短路)33(0R R =。
试求以上3种情况下电压2u 和电流23,i i 。
解:(1)2R 和3R 为并联,其等效电阻842R k ==Ω,则总电流 mA R R u i s 3504210011=+=+=分流有 mA i i i 333.86502132==== V i R u 667.666508222=⨯==(2)当∞=3R ,有03=imA R R u i s 1082100212=+=+=V i R u 80108222=⨯==(3)03=R ,有0,022==u imA R u i s 50210013===2-2 电路如图所示,其中电阻、电压源和电流源均为已知,且为正值。
求:(1)电压2u 和电流2i ;(2)若电阻1R 增大,对哪些元件的电压、电流有影响?影响如何?解:(1)对于2R 和3R 来说,其余部分的电路可以用电流源s i 等效代换,如题解图(a )所示。
因此有 32332R R i R i += 32322R R i R R u s+=(2)由于1R 和电流源串接支路对其余电路来说可以等效为一个电流源,如题解图(b )所示。
电路-第2章习题-电阻电路的等效变换

2-1、求电路的入端电阻R AB 。
R= 2//2+4//6AB答案 3.4Ω2-2、求各电路的入端电阻R AB。
(6//6+9)//102-3、求各电路的入端电阻R AB。
→解:(a)(3//6+1)//6=2Ω(b) 等效电路如图所示:即2-4、试求下图所示电路中的电流I。
答案-1.1A2-5、求图示电路中的电流i。
答案:- 0.1A2-6、电路如图所示,求B点的电位V B。
解:该电路图可以改变成如下图所示的形式2-7、电路如图所示,求电流I和电压U AB。
解:原电路可以等效变换为如下电路152-8、电路如图所示,求AB端的等效电阻R AB。
解:在AB端外加电源,使u、i对二端电路来说是关联参考方向。
由图可得:得到2-9、求图 (a) 和 (b) 所示两电路的输入电阻。
2-10、用电源等效变换法求图示电路中负载R L 上的电压U 。
12A5ΩR L+ -14V +-4Ω14-2Ω 2Ω2Ω2-11、化简为一个等效的电压源支路。
(a) (b) (c) (d)其中111R U I S S =,222R U I S S =,21S S S I I I +=,)(2121R R R R R S +=,S S S I R U =。
恒流源与恒压源的串联和并联两种情况(1) (2)2-12、化简图示电路。
(a) (b) (c) (d)2-13、在图(a )所示电路中,已知V 12=S U ,Ω=31R ,A 5=S I ,Ω=62R ,试求2R 支路中的电流2I 。
(a) (b) (c)解: 3)5312(633)(12112=++=++=S S I R U R R R I A10;2-14、在图示电路中,N为一个实际的直流电源。
当开关S断开时,电压表读数为V1。
试求该直流电源N的电压源模型与电流源模型。
当开关S闭合时,电流表读数为A解:等效电路如图:,2-15、电路如图所示。
已知Ω=61R ,Ω=1.02R ,98.0=α,Ω=53R ,V U 9.4=。
第2章电阻电路的等效变换习题及参考答案

精心整理第2章习题与解答2-1试求题2-1图所示各电路ab 端的等效电阻ab R 。
(a) (b)题2-1图解:(a )14//(26//3)3ab R =++=Ω(b 2-2解:(a (b 2-3(a)(b)解:(a (b 2-4(a) (b)题2-4图解:(a )从左往右流过1Ω电阻的电流为从上往下流过3Ω电阻的电流为36I 32A 36=⨯=+ 从上往下流过12Ω电阻的电流为126I 31A 126=⨯=+ 所以312I I -I =1A =(b )从下往上流过6V 电压源的电流为66I 4A 1.5===(1+2)//(1+2) 从上往下流过两条并联支路的电流分别为2A所以U 22-12=2V =⨯⨯2-5试求题2-5图所示各电路ab 端的等效电阻ab R ,其中121R R ==Ω。
(a) (b)题2-5图解:(a(b 即得所以ab R 2-6解:(a 所以ab R (b 所以ab R 2-7U 及总电压ab U 题2-7图解:将图中的Y 形变成△形,如图所示所以(32.5//526//2)//2655510ab R =++=+=Ω回到原图已知128I I +=348I I +=1310840I I +=245240I I +=联立解得1 2.4I A =2 5.6I A =32I A =46I A =所以121054U I I V =-+=2-8试求题2-8图所示电路的输入电阻in R 。
(a)(b)题2-8图解:(a )如图所示,在电路端口加电压源U ,求I 所以21(1)in U R R R Iμ==+- (b )如图所示,在电路端口加电压源U ,求I12R R U 2-(b 2-62-题2-11图解:先化简电路,如图所示43Ω所以有41(2933i i +-=3i A = 2-12题2-12图所示电路中全部电阻均为1Ω,试求电路中的电流i 。
题2-12图解:先求电路右边电阻块的等效电阻ab R ,如图所示将中间的Y 形化成△形。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
或等效电导 Geq 等于 n 个电导 G1 , G2 ,…, Gn 之和即
Geq G1 G2 .... Gn Gk
k 1
n
式中 Geq
1 1 1 1 , G1 , G2 ,…, Gn 。 Req R1 R2 Rn
2. 电压源串联和电流源并联的等效电源 (1)n 个电压源 us1 , us2 ,…, usn 串联的等效电压源 us geq 是 n 个电压源电压的代数 和。即
并联电阻是网络中所有独立电源置零时端口的输入电阻。这一等效电路,称为诺顿等效电 路。 2.求戴维南等效电路和诺顿等效电路 一个含源性二端网络应用戴维南定理,求它的戴维南等效电路和诺顿等效电路,就是 计算端口的开路电压 U oc 、短路电流 I sc 和端口的输入电阻 Ro . 求 U oc 和 I sc ,分别将含源性二端网络端口开路和短路,应用等效化简、节点分析法和 网孔分析等方法计算得出。 求 Ro 有三种法: (1)通过等效化简来求出 Ro 。将二端网络中所有独立电源置零后的无源二端网络, 应用电阻串、并联或 Y - 变换等进行等效化简,求出端口的输入电阻 Ro . (2)伏安关系法。将无源二端网络端口外加电压源电压 U,产生输入电流 I;或端口 外加电流源电流 I,产生端口电压 U.根据 KVL,KCL 和元件的 VAR,求出端口电压 U 与电流 I 的伏安关系方程,则端口的输入电阻 Ro
R1
R12 R31 R12 R23 R31 R12 R23 R12 R23 R31 R23 R31 R12 R23 R31
R2
R3
(三) 关于电路等效化简的分析方法 1. 为求电路中某一支路的电流和电压,运用等效化简分析方法时,将待求支路古的 固定不动,电路的其余部分根据上述等效变化化简电路的基本方法,按“由远而进”逐步 进行等效化简, 化简成为单回路或单节偶等效电路。 于是, 根据等效电路, 运用 KVL 或 KCL 和元件的 VAR,或分压与分流关系,计算出待求支路的电压和电流。 2. 对于有受控源的含源线形二端网络进行等效化简时,受控源按独立电源处理。但 是,在等效变换化简电路的过程中,受控源的控制量支路应该保留。应注意的是,受控源 的控制量应在端口及端口内部。 3. 对于含受控源的无源二端网络,等效化简为一个等效电阻 R0 。这时可以采用网 络端口外加电压源电压或电流源电流的伏安关系来求解。 (1) 在无源二端网络端口外加电压源 u ,则产生输入电流 i 。运用 KVL,KCL 和元件 VAR,求出端口电压 u 与电流的 i 关系式。则等效电阻为
串联的电压源模型,其中 is
us Rs
, Rs RS 。
(2)若已知电流源 is 与电阻 RS 并联的电流源模型,等效变换为电压源 us 与电阻 Rs 串 联的电压源模型,其中 us RS is , Rs RS 。 两类电源模型等效变换中应注意的几个问题是: 1. 电压源 us 与电流源 is 之间不能等效变换,因为它们端钮的 VAR 没有等效的条件。 2. 电压源 us 与电阻元件 R 或与电流源 is 并联的电路, 由于其端口电压 us , 故对端
n
,是 n 个电阻之和。即
R eq R1 R2 ... Rn Rk
k 1
(2) n 个电阻元件 R1 , RX K , X n 并联电路的等效电阻 R eq 的倒数是 n 个电阻各自倒数 之和,即
n 1 1 1 1 1 ... R eq R1 R2 Rn k 1 Rk
二、学
习
指
导
等效变换化简电路,是电路的基本分析方法之一,是本课程重要的基本内容。本章的 教学内容可以分为如三部分: 1. 二端网络等效的概念; 2. 电阻电路中等效变换和化简的基本方法; 3. 含源线形二端网络包括受控源而端网络的等效化简和电路分析。 着重讨论电路等效和的等效变换的概念、电阻串、并联的等效电阻,两类电源模型的 等效变换方法,遗迹含源线形而端网络的等效化简方法。 (一) 关于二端网络等效的概念 1. 二端网络等效的定义 两个结构不同的二端网络,它们的端口分别外接任何相同的负载或电路时,两端口的
伏安关系相等。在 u , i 平面上,等效的两个二端网络端口的 VAR 特性曲线相同。 2. 等效的范围与作用 等效是指二端网络的端口及端口外部电路而言,对网络端口内部不等效。等效电路只 能用来计算端口及端口外部电路的电流和电压。一个电路对于不同的端口和不同的部分, 有不同的等效电路。 (二) 关于等效变换和化简的基本规律和公式 将一个电路对指定端口内部进行结构变形,成为另一结构的电路,新电路端口的 VAR 与原 电路断口的 VAR 相等,称为等效变换。将一个复杂的电路对指定端口等效变换为一个结构 简单的电路,称为等效化简。根据而端网络等效的定义,等效变换和化简电路有如下的规 律和公式。 1. 电阻串、并联的等效电阻 (1)n 个电阻元件 R1 , RX K , X n 串联电路的等效电阻
R0
u i
若端口外加电压 u 1V ,求出端口的输入电流 i 值。则等效电阻为 R0 1 。
i
(2) 在无源二端网络端口外加电流源电流 i 值。则产生电压 u 。运用 KVL,KCL 和元 件 VAR,求出端口电压 u 与电流 i 的关系式。则等效电阻为 R0 u 。
i
若端口外加电流 i =1A,求出端口电压 u 值。则等效电阻为 R0 u 。 (3) 先任意假定无源二端网络中某一支路电流或电压值, 根据元件的 VAR 和 KVL, KCL。 计算出端口电压和 u 输入电流 i 的数值。则等效电阻为 R0 u 。
i
(四)关于叠加定理的理解与应用 1.对叠加定理的理解 叠加定理是线性电路的基本定理,应理解它的两种基本性质。
(1)可加性:若线性电路中的 n 个独立电源 e1 , e2 ,L , en ,它们分别单独作用时,电 路中某一支路的电流或电压分别为 f (e1 ), f (e2 ),L , f (en ). 则 e1 , e2 ,L , en 共同作用时,电 路中某一支路的电流或电压,是 n 个电源单独作用时数值的代数和。即
2.应用叠加定理分析多电源线性电路 应用叠加定理分析多电源线性电路的一般步骤如下: (1)假定所求支路电流、电压的参考方向,标示于电路图中。 (2)分别作出每一独立电源单独作用时的电路,这时其余所有独立电源置零,即电 压源短路,电流源开路。若含有受控源时,每一独立电源单独作用时,受控源均应保留。 (3)分别计算出每一独立电源单独作用时,待求支路的电流或电压。这时它们的参 考方向均应不变。 (4)进行叠加,求出待求支路在所有电源共同作用时的电流或电压,等于每一独立 电源单独作用时待求支路电流或电压的代数和。 3.叠加定理的应用范围 叠加定理适用于任何多电源线性电路的分析,用来计算任一支路的电流或电压,而不 能直接用来计算功率。因功率是电流或电压的二次函数。 (五)关于戴维南定理和诺顿定理 1.戴维南定理和诺顿定理的表述 戴维南定理:任何一个含源性二端网络,对端口及端口外部电路而言,都可以用一电 压源与一电阻元件串联的等效电路来代替。 电压源的电压是二端网络端口的开路电压 U oc , 串联电阻是网络中所有独立电源置零(电压源短路,电流源开路。但受控源则应保留)时 端口的输入电阻。这一等效电路,称为戴维南等效电路。 诺顿定理:任何一个含源线性二端网络,对端口及端口外部电路而言,都可以用一电 流源与一电阻元件并联等效电路来代替。电流源的电流是二端网络端口的短路电流 I sc ,
和
R31
三角形
连接的电阻网络。这时
R12 R1 R2
R1 R2 R3 R2 R3 R1 R3 R1 R2
R知由 R12 , R23 和 R31 三角形连接的电阻网络,可以等效变换为 R1 , R2 和 R3
星形连接的电阻网络。这时
口而言,可将并联电阻 R 或电压源 us 拆除,等效电路用一电压源 u s 来表示。 3. 电流源 is 与电阻元件 R 或电压源 u s 置零,等效电路用一电流源 is 来表示。 4. 星形与三角形连接电阻网络的等效变换 (1)已知
R1
,
R2
和
R3
星形连接的电阻网络,可以等效变换为由
R12
,
R23
U . I
(3) 开路电压和短路电流法。 分别计算出含源线性二端网络的开路电压 U oc 和短路电 流 I sc ,则端口的输入电阻 R0 U oc I sc . 对于含受控源的二端网络,求 Ro 则应采用后两种方法。 (4) 含受控源无源二端网络的等效化简,求端口的输入电阻,以及戴维南定理和诺顿 定理的计算是学习的一个难点。 本章学习的重点内容是:二段网络等效的概念,电阻串联、并联的等效电阻,遗迹电 路等效化简的分析方法,叠加定理、戴维南定理和诺顿定理的计算。
us geq us1 us2 ... usn usk
k 1
n
(2)n 个电流源 is1 , is2 ,…, isn 并联的等效电流源 is geq 是 n 个电流源电流的代数和, 即
is geq is1 is2 ... isn isk
k 1
n
3.电压源模型与电流源模型的等效变换 (1)若已知电压源 us 与电阻 Rs 串联的电压源模型,等效变换为电流源 is 与电阻 RS
第2章
电阻电路的等效变换 学习指导与题解
一、基
本
要
求
1.深刻理解两个结构不同二端网络等效的概念。明确电路等效变换和等效化简的含义。 2.熟练掌握电阻串联、并联及并联等效化简为一个等效电阻的方法。 3.熟练掌握电压源串联和等效电流源的方法。能正确确定等效电压源电路电流的大小 和方向。 4.熟练掌握两类实际电源模型等效互换的方法。即电压雅模型等变换为电流源模型; 电流源模型等效变换为电压源模型。能正确确定变换后电压源模型中电压和电流源电流的 大小和方向。 5.掌握星形(Y)电阻网络与三角形( V)电阻网络等效互换的方法。即星形连接电阻 网络等效变换为三角形连接电阻网络;三角形连接电阻网络等效变换与星形连接电阻网 络。 6.掌握含源线形二端网络等效化简的方法。即将结构较复杂的含源线形二端网络等效 化简为一电压源与一电阻元件串联的最简单电路,或为一电流源与一电阻并联的最简单节 偶电路。能见含源受控源线形二端网络进行等效化简。 7.掌握用等效化简的方法分析电阻电路。 8. 理解线性电路叠加性的意义。能正确运用叠代定理来分析计算多电源线性电路中的 电流和电压,包括含有受控源的电路。 9. 明确戴维南定理和诺顿定理的含义。能正确运用戴维南定理及诺顿定理来分析电路, 包括含有受控源电路。熟练掌握求含源二端网络的戴维南等效电路和诺顿等效电路,即计 算二端网络端口的开路电压 U oc 、短路电流 I sc 和端口内电路的等效电阻 Ro 的方法。
