数字图像处理第十一章
《数字图像处理》课程教学大纲
二、课程章节主要内容及学时分配第一章、数字图像处理方法概述讲课3课时了解本课程研究的对象、内容及其在培养软件编程高级人才中的地位、作用和任务;了解数字图像处理的应用;了解数字图像的基本概念、与设备相关的位图(DDB)、与设备无关的位图(DIB);了解调色板的基本概念和应用;了解CDIB类与程序框架结构介绍;了解位图图像处理技术。
重点:CDIB类与程序框架结构介绍。
难点:调色板的基本概念和应用。
第二章、图像的特效显示讲课3课时、实验2学时了解扫描、移动、百叶窗、栅条、马赛克、渐显与渐隐、浮雕化特效显示。
重点:渐显与渐隐。
难点:马赛克。
第三章、图像的几何变换讲课2课时了解图像的缩放、平移、镜像变换、转置、旋转。
重点:镜像变换。
难点:旋转。
第四章、图像灰度变换讲课3课时、实验2学时了解非0元素取1法、固定阈值法、双固定阈值法的图像灰度变换;了解灰度的线性变换、窗口灰度变换处理、灰度拉伸、灰度直方图、灰度分布均衡化。
重点:灰度直方图。
难点:灰度分布均衡化。
第五章、图像的平滑处理讲课3课时了解二值图像的黑白点噪声滤波、消除孤立黑像素点、3*3均值滤波、N*N 均值滤波器、有选择的局部平均化、N*N中值滤波器、十字型中值滤波器、N*N最大值滤波器、产生噪声。
重点:消除孤立黑像素点、中值滤波器。
难点:有选择的局部平均化。
第六章、图像锐化处理及边缘检测讲课3课时、实验2学时了解梯度锐化、纵向微分运算、横向微分运算、双方向一次微分运算、二次微分运算、Roberts边缘检测算子、Sobel边缘检测算子、Krisch边缘检测、高斯-拉普拉斯算子。
重点:Roberts边缘检测算子、高斯-拉普拉斯算子。
难点:梯度锐化。
第七章、图像分割及测量讲课4课时了解图像域值分割、轮廓提取、轮廓跟踪、图像的测量。
重点:轮廓提取、轮廓跟踪。
难点:图像的测量。
包括:图像的区域标记、图像的面积测量及图像的周长测量。
第八章、图像的形态学处理讲课3课时了解图像腐蚀、图像的膨胀、图像开启与闭合、图像的细化、图像的粗化、中轴变化。
(完整版)数字图像处理:部分课后习题参考答案
第一章1.连续图像中,图像为一个二维平面,(x,y)图像中的任意一点,f(x,y)为图像于(x,y)于处的值。
连续图像中,(x,y)的取值是连续的,f(x,y)也是连续的数字图像中,图像为一个由有限行有限列组成的二维平面,(i,j)为平面中的任意一点,g(i,j)则为图像在(i,j)处的灰度值,数字图像中,(i,j) 的取值是不连续的,只能取整数,对应第i行j列,g(i,j) 也是不连续的,表示图像i行j列处图像灰度值。
联系:数字图像g(i,j)是对连续图像f(x,y)经过采样和量化这两个步骤得到的。
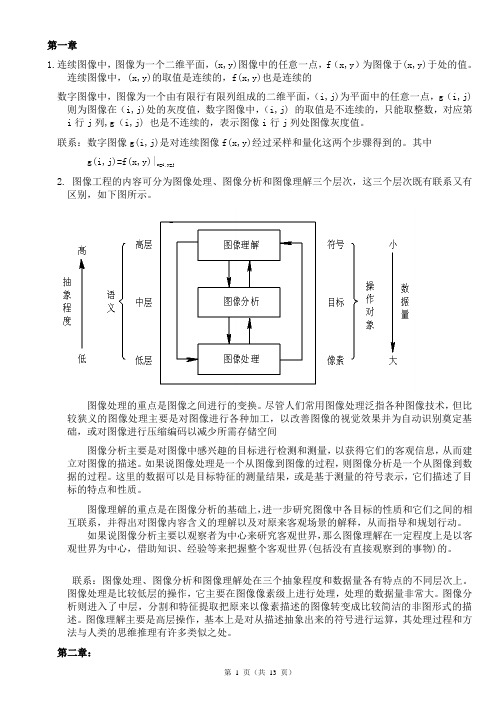
其中g(i,j)=f(x,y)|x=i,y=j2. 图像工程的内容可分为图像处理、图像分析和图像理解三个层次,这三个层次既有联系又有区别,如下图所示。
图像处理的重点是图像之间进行的变换。
尽管人们常用图像处理泛指各种图像技术,但比较狭义的图像处理主要是对图像进行各种加工,以改善图像的视觉效果并为自动识别奠定基础,或对图像进行压缩编码以减少所需存储空间图像分析主要是对图像中感兴趣的目标进行检测和测量,以获得它们的客观信息,从而建立对图像的描述。
如果说图像处理是一个从图像到图像的过程,则图像分析是一个从图像到数据的过程。
这里的数据可以是目标特征的测量结果,或是基于测量的符号表示,它们描述了目标的特点和性质。
图像理解的重点是在图像分析的基础上,进一步研究图像中各目标的性质和它们之间的相互联系,并得出对图像内容含义的理解以及对原来客观场景的解释,从而指导和规划行动。
如果说图像分析主要以观察者为中心来研究客观世界,那么图像理解在一定程度上是以客观世界为中心,借助知识、经验等来把握整个客观世界(包括没有直接观察到的事物)的。
联系:图像处理、图像分析和图像理解处在三个抽象程度和数据量各有特点的不同层次上。
图像处理是比较低层的操作,它主要在图像像素级上进行处理,处理的数据量非常大。
图像分析则进入了中层,分割和特征提取把原来以像素描述的图像转变成比较简洁的非图形式的描述。
(完整版)数字图像处理每章课后题参考答案

数字图像处理每章课后题参考答案第一章和第二章作业:1.简述数字图像处理的研究内容。
2.什么是图像工程?根据抽象程度和研究方法等的不同,图像工程可分为哪几个层次?每个层次包含哪些研究内容?3.列举并简述常用表色系。
1.简述数字图像处理的研究内容?答:数字图像处理的主要研究内容,根据其主要的处理流程与处理目标大致可以分为图像信息的描述、图像信息的处理、图像信息的分析、图像信息的编码以及图像信息的显示等几个方面,将这几个方面展开,具体有以下的研究方向:1.图像数字化,2.图像增强,3.图像几何变换,4.图像恢复,5.图像重建,6.图像隐藏,7.图像变换,8.图像编码,9.图像识别与理解。
2.什么是图像工程?根据抽象程度和研究方法等的不同,图像工程可分为哪几个层次?每个层次包含哪些研究内容?答:图像工程是一门系统地研究各种图像理论、技术和应用的新的交叉科学。
根据抽象程度、研究方法、操作对象和数据量等的不同,图像工程可分为三个层次:图像处理、图像分析、图像理解。
图像处理着重强调在图像之间进行的变换。
比较狭义的图像处理主要满足对图像进行各种加工以改善图像的视觉效果。
图像处理主要在图像的像素级上进行处理,处理的数据量非常大。
图像分析则主要是对图像中感兴趣的目标进行检测和测量,以获得它们的客观信息从而建立对图像的描述。
图像分析处于中层,分割和特征提取把原来以像素描述的图像转变成比较简洁的非图形式描述。
图像理解的重点是进一步研究图像中各目标的性质和它们之间的相互联系,并得出对图像内容含义的理解以及对原来客观场景的解释,从而指导和规划行为。
图像理解主要描述高层的操作,基本上根据较抽象地描述进行解析、判断、决策,其处理过程与方法与人类的思维推理有许多相似之处。
第三章图像基本概念1.图像量化时,如果量化级比较小时会出现什么现象?为什么?答:当实际场景中存在如天空、白色墙面、人脸等灰度变化比较平缓的区域时,采用比较低的量化级数,则这类图像会在画面上产生伪轮廓(即原始场景中不存在的轮廓)。
胡学龙《数字图像处理(第二版)》课后习题解答

2.1 设有大小为 32×32 的图标,图标的每个像素有 8 种颜色,共有多少种不同的图标?
如果每 100 万个可能的图标中有一个有意义,识别一个有意义的图标需要 0.1 s,则选出所
有有意义的图标需要多长时间?
解:图标数为
832×32 = 10925 种
有意义的图标数 10925/106 = 10919 种
第 1 章 概述
1.1 连续图像和数字图像如何相互转换? 答:数字图像将图像看成是许多大小相同、形状一致的像素组成。这样,数字图像可以 用二维矩阵表示。将自然界的图像通过光学系统成像并由电子器件或系统转化为模拟图像 (连续图像)信号,再由模拟/数字转化器(ADC)得到原始的数字图像信号。图像的数字 化包括离散和量化两个主要步骤。在空间将连续坐标过程称为离散化,而进一步将图像的幅 度值(可能是灰度或色彩)整数化的过程称为量化。
2
1.PHOTOSHOP:当今世界上一流的图像设计与制作工具,其优越性能令其产品望尘 莫及。PHOTOSHOP 已成为出版界中图像处理的专业标准。高版本的 PHOTOSHOP 支持多 达 20 多种图像格式和 TWAIN 接口,接受一般扫描仪、数码相机等图像输入设备采集的图 像。PHOTOSHOP 支持多图层的工作方式,只是 PHOTOSHOP 的最大特色。使用图层功能 可以很方便地编辑和修改图像,使平面设计充满创意。利用 PHOTOSHOP 还可以方便地对 图像进行各种平面处理、绘制简单的几何图形、对文字进行艺术加工、进行图像格式和颜色 模式的转换、改变图像的尺寸和分辨率、制作网页图像等。
4
110 106 129 129 127 122 117 88 84 112 111 131 130 128 118 111 97 97 133 127 138 131 124 111 102 100 97 166 151 144 126 124 111 99 96 93 158 143 139 130 120 100 96 97 100 128 121 126 122 88 62 65 68 79 106 92 107 114 82 52 42 41 56
数字图像处理
1 低通滤波器法
(2)振铃
ILPF空域上冲激响应卷积产生两个现象: 一是边缘渐变部分的对比度; 二是边缘部分加边(ringing)。
其原因是冲激响应函数的多个过零点。
1 低通滤波器法
f(x)
h(x)
g(x)
1 低通滤波器法
3)巴特沃思低通滤波器(BLPF)
n阶巴特沃思(Butterworth)滤波器 u v 1 D0 n 11 , 阶巴特沃思滤波器
2 高通滤波器法
-4
4
0.8 0.6 0.4 0.2 -2 -2 0 v u 2 2
-4
4
0.8 0.6 0.4 0.2
-4
-2
0
2 t
4
2 高通滤波器法
3)巴特沃思高通滤波器(BHPF)
n阶巴特沃思(Butterworth)高通滤波器 D0 1 2 2 u v n 11 , 阶巴特沃思高通滤波器 1 H u, v 2 D0 1 2 2 u v H u, v 1
G u, v F u, v H u, v F u , v 是输入,G u , v 是输出 H u , v 是线性系统的传递函数
1 低通滤波器法
2)理想低通滤波器(ILPF)
定义:以D0为半径的圆内所有频率分量无损的通过, 圆外的所有频率分量完全衰减。
2 2
e
t 2 2 2 2
2 高通滤波器法
1.4 1.2 1 0.8 0.6 0.4 0.2 -4 -2 0 2 u 4
0.6
0.4
0.2
数字图像处理_课件_11

33
距离与角度标记图
数第 字十 图一 像章 处表 理示
和 描 述
r θ
A r(θ)
A
0 3 π 5 3 7 2 4 2 4 θ 42 4
(a) r(θ)为常量;
r(θ) 2A
A
0 4
3 24
r θ A
π 5 3 7 2 θ 42 4
(b) 标记图由重复出现的模式r(θ)=Asecθ, 0≤θ≤π/4
描
储b0和b1的位置,以便在步骤5中使用。
述
2. 令b=b1和c=c1 [见图 (c)]。
7
数 第 3. 从c开始按顺时针方向行进,令b的8个邻点为
字十 图一
n1, n2, …, n8。找到标为1的第一个nk。
像章 处表
4.
令b=nk和c=nk-1。
理示 和
5.
重复步骤3和步骤4,直到b=b0且找到的下一
10
数第 字十 图一 像章 处表 理示
和 描 述
➢ 如果给定一个区域而非其边界,那么边界追踪 算法会工作得很好。也就是说,该过程提取一 个二值区域的外边界。
➢ 如果目的是找到一个区域中的孔洞的边界(这 种边界称为该区域的内边界),一种简单的方 法是提取这些孔洞(见9.5.9节),并将它们当 做0值背景上的1值区域来处理。对这些区域应 用边界追踪算法将得到原始区域的内边界。
和r(θ)=Acscθ, π/4<θ≤π/2构成。
34
两个二值区域的标记图
1. 根据其外部特征(其边界)来表示区域;
2. 根据其内部特征(如组成该区域的像素)表 示它。
3
数 第 ➢ 选择用来作为描绘子的特征都应尽可能
字十 图一
图像识别ppt课件

最小距离分类器(最简单) 基于相关的方法 ……
•16
•ppt课件.
数字图像处理
(1) 最小距离分类器
在欧氏空间计算未知量和每一个原型矢量间的距离。 例如,假设每个模式类的原型定义为该类模式的平均矢量:
则欧氏空m 间j 距N 1离j x 判wjx据j,—j—1计,2算, 距,W离测度为:
花瓣宽度(cm)
•ppt课件.
数字图像处理
花瓣长度(cm)
图11.4 Iris Versicolor (杂色的) 和Iris Setosa (多刺的)类的 最小距离分类器的决策边界。黑点和方块是平均值。
•18
边界方程: d12(x) = d1(x)-d2(x) = 2.8x1+1.0x2-8.9 = 0
•26
j 1
•ppt课件.
数字图像处理
(4) BAYES决策规则
每个对象应该归入产生条件风险最小的类别中。
用Rm(x1, x2, … , xn)表示相应于特征向量(x1, x2, … , xn)T的最小风险。
使用Bayes决策的分类器长期风险称为Bayes风险:
R R m ( x 1 ,x 2 , ,x n )p ( x 1 ,x 2 , ,x n ) d 1 d x 2 x d nx
•ppt课件.
数字图像处理
图11.5 美国Banker协会 的E-13B字体的字符 集和对应波形。
字符设计在97个字中以 便读取。每个字符 用含有精细磁性材 料的墨水印刷。
(设计者保证大的均值 分离和小的类分布 的一个示例)
•19
(2) 相关匹配
M×N大小的图像f(x,y)和大 小为J×K的子图w(x,y)之间
迅速增长。
《数字图像处理》-教学大纲

《数字图像处理》课程教学大纲Digital image processing一、教学目标及教学要求数字图像处理课程是智能科学与技术、数字媒体技术等专业的专业必修课。
主要目标及要求是通过该课程的学习,使学生初步掌握数字图像处理的基本概念、基本原理、基本技术和基本处理方法,了解数字图像的获取、存储、传输、显示等方面的方法、技术及应用,为学习相关的数字媒体、视频媒体和机器视觉等课程,以及今后从事数字媒体、视频媒体、图像处理和计算机视觉等领域的技术研究与系统开发打下坚实的理论与技术基础。
二、本课程的重点和难点(一)课程教学重点教学重点内容包括:图像的表示,空间分辨率和灰度级分辨率,图像直方图和直方图均衡,基于空间平滑滤波的图像增强方法,基于空间锐化滤波的图像增强方法,图像的傅里叶频谱及其特性分析,图像编码模型、霍夫曼编码和变换编码,图像的边缘特征及其检测方法,彩色模型,二值形态学中的有腐蚀运算和膨胀运算。
(二)课程教学难点教学难点包括:直方图均衡,二维离散傅里叶变换的若干重要性质、图像的傅里叶频谱及其特性分析,变换编码,小波变换的概念、嵌入式零树小波编码,图像的纹理特征及其描述和提取方法,Matlab图像处理算法编程。
三、主要实践性教学环节及要求本课程的实验及实践性环节要求使用Matlab软件平台,编写程序实现相关的数字图像处理算法及功能,并进行实验验证。
课程实验与实践共10学时,分别为:实验一:图像基本运算实验(2学时)。
实验二:图像平滑滤波去噪实验(2学时)。
实验三:图像中值滤波去噪实验(2学时)。
实验四:图像边缘检测实验(2学时)。
相关图像处理算法的课堂演示验证(2学时)。
要求每个学生在总结实验准备、实验过程和收获体会的基础上,写出实验报告。
四、采用的教学手段和方法利用多媒体课件梳理课程内容和讲授思路,合理运用启发式教学方式激发学生的思考力,采用讨论式教学方式增强教学过程的互动效果,理论教授与应用实例编程实践相结合,提高学生的分析和解决问题的能力。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
11.1.1 Cell Arrays and Structures
• Cell Arrays
Cell Arrays provide a way to combine a mixed set of objects under one variable name. A single variable C C={f, b, char_array} Here f , an uint8 image of size 512*512; b, a sequence of 2-D coordinates in the form of rows of a 188*2 array char_array, a cell array containing two character name.
© Mingyan Jiang, SDU, Copyright Reserved
5 / 81
• function s=image_stats(f) s.dim=size(f); s.AI=mean(f); s.AIrows=mean(f); s.AIcols=mean(f);
s is a structure. AI (a scalar), dim(a 1*2 vector), AIrows(an M*1 vector), Aicols(a 1*N).
© Mingyan Jiang, SDU, Copyright Reserved
11 / 81
© Mingyan Jiang, SDU, Copyright Reserved
12 / 81
• The chain code of a boundary depends on the starting point. • Function fchcode c=fchcode(b, conn, dir) Computes the Freeman chain code of an np*2 set of ordered boundary points stored in array b.
© Mingyan Jiang, SDU, Copyright Reserved
14 / 81
Example 11.3 Freeman chain code and some of its variations
• >>h=fspecial(‘average’, 9); >>g=imfilter(f, h, ‘replicate’); • >>g=im2bw(g, 0.5); >>B=boundaries(g); >>d=cellfun(‘length’, B); >>[max_d, k]=max(d); >>b=B{1};
© Mingyan Jiang, SDU, Copyright Reserved
13 / 81
• The output c is a structure with the following fields c.fcc=Freeman chain code (1*np) c.diff=First difference of code c.fcc (1*np) c.mm=Integer of minimum magnitude (1*np) c.diffmm=First difference of code c.mm(1*np) c.x0y0=Coordinates where the code starts (1*2)
Notes the use of a dot to separate the structure from its
various fields. The field names arbitrary, but they must begin with a nonnumeric character.
© Mingyan Jiang, SDU, Copyright Reserved
© Mingyan Jiang, SDU, Copyright Reserved 18 / 81
© Mingyan Jiang, SDU, Copyright Reserved
10 / 81
11.2.1 Chain Codes
• Chain codes are used to represent a boundary by a connected sequence of straight-line segments of specified length and direction. The direction of each segment is coded by using a numbering scheme such as the ones shown in Figs. 11.1(a) and (b).
• The goal of a polygonal approximation is to use the fewest possible to capture the “essence” of the boundary shape. • A particularly attractive approach to polygonal approximation is to find the minimum-perimeter polygon (MPP) of a region or boundary.
© Mingyan Jiang, SDU, Copyright Reserved
9 / 81
11.2 Representation
• Standard practice is to use schemes that compact the data into representations that are considerably more useful in the computation of descriptors.
© Mingyan Jiang, SDU, Copyright Reserved
7 / 81
11.1.3 Some Basic Utility MFunctions
• Suppose that we want to find the boundary of the object with the longest boundary in image f: >>B=boundaries(f); >>d=cellfun(‘length’, B); >>[max_d, k]=max(d); >>v=B{k(1)};
© Mingyan Jiang, SDU, Copyright Reserved
4 / 81
Structures
• Structures are similar to cell arrays in the sense that they allow grouping of a collection of dissimilar data into a single variable. However cells are addressed by numbers, the elements of structures are addressed by names called fields.
© Mingyan Jiang, SDU, Copyright Reserved
15 / 81
• >>[M N]=size(g); >>g=bound2im(b, M, N, min(b(:, 1)), min(b(:, 2))); >>[s,su]=bsubsamp(b,50); • >>g2=bound2im(s, M, N, min(s(:, 1)), min(s(:, 2))); • >>cn=connectpoly(s(:, 1), s(:, 2)); >>g2=bound2im(cn, M ,N min(cn(:, 1)), min(cn(:, 2))); >>c=fchcode(su);
© Mingyan Jiang, SDU, Copyright Reserved
8 / 81
• • • • • • •
b8=boundary2eight(b) b4=boundary2four(b) G=boundary2im(b, M, N, x0, y0) b=cat(1,B{:}) [s, su]=bsubsamp(b,gridsep) Z=connectpoly(s(:,1), s(:, 2)) [x, y]=intline(x1, x2, y1, y2)
© Mingyan Jiang, SDU, Copyright Reserved 16 / 81
© Mingyan Jiang, SDU, Copyright Reserved
17 / 81
11.2.2 Polygonal Approximations Using Minimum-Perimeter Polygons
© Mingyan Jiang, SDU, Copyright Reserved
2 / 81
11.1 Background
• A region is a connected component, and the boundary (border or contour) of a region is the set of pixels in the region that have one or more neighbors that are not in the region. • We allow pixels to have gray-scale or multispectral values. • Boundary is a conneoints form a clockwise or counterclockwise sequence we say to be ordered.
