纸浆浓度调节统的模糊控制及MATLAB仿真
模糊控制Matlab仿真
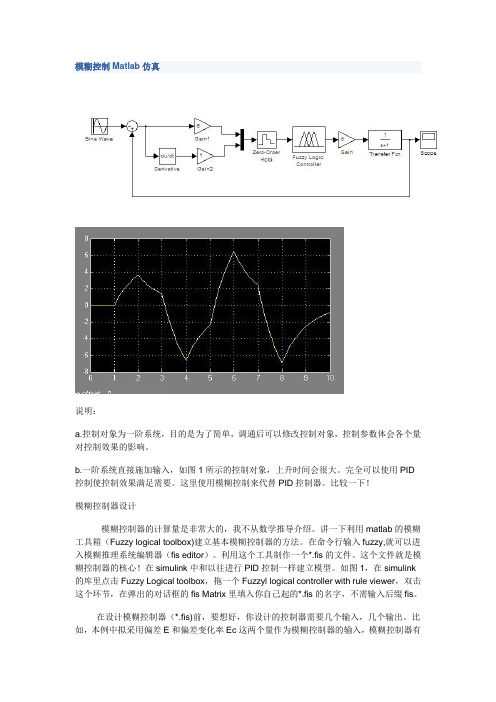
模糊控制Matlab仿真说明:a.控制对象为一阶系统,目的是为了简单,调通后可以修改控制对象,控制参数体会各个量对控制效果的影响。
b.一阶系统直接施加输入,如图1所示的控制对象,上升时间会很大。
完全可以使用PID 控制使控制效果满足需要。
这里使用模糊控制来代替PID控制器。
比较一下!模糊控制器设计模糊控制器的计算量是非常大的,我不从数学推导介绍。
讲一下利用matlab的模糊工具箱(Fuzzy logical toolbox)建立基本模糊控制器的方法。
在命令行输入fuzzy,就可以进入模糊推理系统编辑器(fis editor)。
利用这个工具制作一个*.fis的文件。
这个文件就是模糊控制器的核心!在simulink中和以往进行PID控制一样建立模型。
如图1,在simulink 的库里点击Fuzzy Logical toolbox,拖一个Fuzzyl logical controller with rule viewer,双击这个环节,在弹出的对话框的fis Matrix里填入你自己起的*.fis的名字,不需输入后缀fis。
在设计模糊控制器(*.fis)前,要想好,你设计的控制器需要几个输入,几个输出。
比如,本例中拟采用偏差E和偏差变化率Ec这两个量作为模糊控制器的输入,模糊控制器有一个输出。
很明显,这是利用模糊控制器代替PD控制的。
对应的模糊控制器的设计也要具有两个输入一个输出。
利用matlab的Fuzzy logical toolbox 设计模糊控制器(生成*.fis文件)的关键步骤:a.添加输入输出。
图3.fis编辑器默认的具有一个输出,添加第二个输入,并且分别命名为E,Ec,U。
b.确定隶属函数。
双击黄色和绿色的方框就可以进入隶属函数编辑对话框了。
设置E,Ec 的range为[-6,6],u的range为[-1,1]。
然后每一个变量再添加4个输入隶属函数,总共7个。
matlab提供了11种隶属函数,第一次用选择常用的三角形trimf,区别不大的。
实验一--模糊控制器的MATLAB仿真

实验一 模糊控制器的MATLAB 仿真一、实验目的本实验要求利用MATLAB/SIMULINK 与FUZZYTOOLBOX 对给定的二阶动态系统,确定模糊控制器的结构,输入和输出语言变量、语言值及隶属函数,模糊控制规则;比较其与常规控制器的控制效果;研究改变模糊控制器参数时,系统响应的变化情况;掌握用 MATLAB 实现模糊控制系统仿真的方法。
实验时数:3学时。
二、实验设备:计算机系统、Matlab 仿真软件 三、实验原理模糊控制器它包含有模糊化接口、规则库、模糊推理、清晰化接口等部分,输人变量是过程实测变量与系统设定值之差值。
输出变量是系统的实时控制修正变量。
模糊控制的核心部分是包含语言规则的规则库和模糊推理。
模糊推理就是一种模糊变换,它将输入变量模糊集变换为输出变量的模糊集,实现论域的转换。
工程上为了便于微机实现,通常采用“或”运算处理这种较为简单的推理方法。
Mamdani 推理方法是一种广泛采用的方法。
它包含三个过程:隶属度聚集、规则激活和输出总合。
模糊控制器的体系结构如图1所示。
图1 模糊控制器的体系结构四、实验步骤(1)对循环流化床锅炉床温,对象模型为()()1140130120++s s采用simulink 图库,实现常规PID 和模糊自整定PID 。
(2)确定模糊语言变量及其论域:模糊自整定PID 为2输入3输出的模糊控制器。
该模糊控制器是以|e|和|ec|为输入语言变量,Kp 、Ki 、Kd 为输出语言变量,其各语言变量的论域如下:误差绝对值:e={0,3,6,10};误差变化率绝对值:ec={0,2,4,6};输出Kp:Up={0,0.5,1.0,1.5};输出Ki:Ui={0,0.002,0.004,0.006};输出Kd:Ud={0,3,6,9}。
(3)语言变量值域的选取:输入语言变量|e|和|ec|的值域取值“大”(B)、“中”(M)、“小”(s)和“零”(Z) 4种;输出语言变量Kp、Ki、Kd的值域取值为“很大”(VB)、“大”(B)、“中”(M)、“小”(s) 4种。
MATLAB设计模糊控制器并用simulink仿真
MATLAB设计模糊控制器并用simulink仿真
环境:MATLAB R2012a
目录
一、设计模糊控制器
1.1 创建项目文件夹
1.2 打开MATLAB
1.3 设计模糊控制器
二、设置控制系统
三、simulink仿真
一、设计模糊控制器
1.1 创建项目文件夹
在此路径如图
1.2 打开MATLAB
打开MATLAB R2012a切换当前目录为上一步路径,如图
1.3 设计模糊控制器
打开模糊控制器设计对话框
根据模糊控制器的输入输出设计模糊控制器,在此以二输入一输出为例。
完成后如图(左)所示,然后对每个输入输出变量设置隶属函数,如图(右)。
添加论域数量
设置隶属函数
完成后如图所示
设计模糊规则
保存刚刚设计的模糊控制器,如下图所示
加载模糊控制器到MATLAB中
二、设置控制系统
打开simulink仿真器
设计控制系统
设计完成如图所示
添加第一节中设计的模糊控制器,如下图
自此控制系统设计结束
三、simulink仿真
在仿真之前需要进行如下设置
开始仿真。
基于MATLAB的模糊控制系统的仿真_张建仁

7
4 结 论 本文主要介绍了 SIMULINK 仿真模型的建立方 法及如何利用 GUI 建立 FIS , 可以看出这种方法相 对于工具函数而言更加简便 、直观 。 通过对纸浆浓 度调节系统仿真结果分析 , 可以说明 , 对于该系统 , 采用模糊控制可以得到比传统的 PID 控制更好的控 制效果 。 ( 上接第 4 页) “ 总体的节省 , 长远的效益” 。 这里从用户选择控制 系统的评估原则角度来说明现场总线控制系统的优 越性 。 如表 1 所示 , 按重要性进行排序并予以加权 + 3 、+ 2 、+ 1 、0 , 以此对 FCS 与 DCS 进行对比 , 定性 地阐述了 FCS 的优越性 。
选取大小为 0 . 3 的常值信号作为系统的设定输 入 , 选取 0 . 012 的阶跃信号对系统作定值扰动 。 首 先在 SIMULINK 环境下创建一个新的 工作区域 , 然 后在 SIMULINK 模块库中选择所需的 模块 , 建立如 图 5 所示的系统仿真模型 。 双击图中的任何模块 ,
都可以根据系统的要求修改或设定其参数 , 该仿真 图中的模糊逻辑控制器( Fuzzy logic controller) 模块中 隐含了输入输出之间的控 制关系 FIS , 它可以 用行 命令编辑函数或 GUI 编辑函数事先建立 , 本文主要 介绍如何利用 GUI 编辑函数直观迅速地建立 FIS 。
真 , 仿真结束时会听到“ 吱”的提示音 , 用户可以通过 示波器观察仿真的结果 , 也可以通 过 plot( ) 函数绘 制系统的仿真曲线如图 6 所示 。 通过这两种途径得 到的曲线是相同的 。 图 7 为系统采用 PID 控制时的 仿真曲线图 。 通过对两条仿真曲线的比较 , 我们可 以看出 , 进行模糊 控制的系统进入 稳态快 , 开 机后 20s 左右即可进入稳态 , 进入稳态后 , 工作稳定 ; 而 采用 PID 控制的系统进入稳态慢 , 有长时间的小幅 振荡现象 。
控制系统仿真设计-基于模糊控制器的纸浆浓度控制系统

控制系统仿真课程设计说明书题目:基于模糊控制器的纸浆浓度控制系统基于模糊控制器的纸浆浓度控制系统摘要:针对纸浆生产过程中与产品质量密切相关的纸浆浓度和流量的稳定性,为解决纸浆浓度控制和测量存在的问题,设计了基于模糊控制技术的纸浆浓度流量计算机控制系统。
该系统根据生产工艺要求采用计算机控制和浓度模糊控制器,对制浆生产过程需要的纸浆浓度、流量以及计算绝干量进行控制。
实际运行结果表明,系统运行可靠,浓度、流量等控制量波动小、精度高,能够满足生产要求,达到了设计目的。
Abstract : To the stability of the consistency and flowing velocity of paper pulp affecting the quality of paper , computer control system of paper pulp consistency and flowing velocity is designed based on fuzzy control technology , according to the problems existing in controlling and measuring the consistency of paper pulp during paper manufacture. The consistency and flowing velocity of paper pulp must be controlled and the dry component of paper pulp must be calculated in paper manufacturing. According to the requires of technics , a computer control system with a fuzzy controller of consistency and flowing velocity is designed. Practical running shows that the system is reliable , and with low disturbance and high precision of the control variables such as consistency and flowing velocity. …………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………………Key words : computer control ; fuzzy controllfer ; kingview ; dry component目录目录 (II)第一章前言 (1)1.1 引言 (1)1.2 模糊控制器的优点 (1)第二章模糊控制器的简介 (2)2.1 模糊控制器的基本结构和组成 (2)第三章模糊控制器的设计 (3)3.1 设计参数 (3)3.2 确定模糊控制器 (4)3.3系统的仿真 (5)总结 (7)参考文献 (8)第一章前言1.1引言针对纸浆浓度控制系统具有大纯滞后和模型不确定的特性,传统的PID控制已经不能很好的控制纸浆浓度,为了解决纸浆浓度控制和测量存在的问题,设计了基于模糊控制技术的纸浆浓度控制系统。
第三章模糊控制模糊控制的MATLAB仿真优秀课件

>> area=pi*r^2; % 计算面积
Hale Waihona Puke 三、变量和数值显示格式1、变量
(1)变量名称
MATLAB对使用变量名称的规定:
1. 变量名称的英文大小写是有区别的(apple, Apple, AppLe,三个变量不同)。
2. 变量的长度上限为 31 个字元。
3. 变量名的第一个字必须是一英文字,随后可 以掺杂英文字、数字或是底线。变量中不能 包含有标点符号。
>> r=2, area=pi*r^2
>> r=2; area=pi*r^2;
请注意上述二式的差异,前者有计算值显示, 而后者则无。
另外一个符号注解是由%起头,也就是说在%之后 的任何文字都被视为程式的注解。注解的功能是 简要的说明程式的内容。任何可能产生混淆的地 方都应该加注解,适量的注解可在以后想了解程 式时能节省一些不必要的时间。例如:
❖ format只是影响结果的显示,不影响其计算与存储; MATLAB总是以双字长浮点数(双精度)来执行所 有的运算。
MATLAB可以将计算结果以不同的精确度的数字格式显示,我们可 以直接在指令视窗键入以下的各个数字显示格式的指令,以π值 为例 :
>> pi ans = 3.1416 >> format long >> pi ans = 3.14159265358979 >> format short e >> pi ans = 3.1416e+000
如果结果为整数,则显示没有小数;如果结果不是整数, 则输出形式有:
四、简单的数学运算(例exp02_01.m)
自调整模糊PID控制及MATLAB仿真

<,i<,% c<,R#<>i<>% c<>R#<P i<P% c<PR$ 从而实现 <,R"<>R"<PR的自调整$ 其中自调整模糊 M#!控制 器结构如图 )!
图) %模糊 M#!控制器的设计 (&$ 输入输出变量的确定 根据要求#将 M#!参数模糊控制器使用三输出与双输入形 式$ 控制器使用误差 7和误差率 ^C作为输入#M#!控制器使 用 M"#"!三个参数作为输出$ (&) 输入输出变量的模糊语言描述 误差 7和误差变化 ^C和模糊子集是2 >D#>F#>E#ME# R"#MF#MD 3 # 代 表 负" 负" 负" 正" 零" 正" 正$ 域 的 ^和 ^C 是'(( #和量化水平2 2("2)"2$#%#$#)#(3 $ 建立后#隶属函数是模 糊逻辑工具箱中的隶属函数编辑器中选择#以及电子商务的隶 属函数是 _:QUUOVP7) _:QUU@W* $ 而隶属函数为三角形) O;/@W* # 分别得到 7"7,".Pp"./p".Xp的隶属函数图$
关键词自调整模糊控制M#!控制器DBZKBFE/@Q9/-. 自调整模糊 M#!控制系统的仿真
55M#!控制技术是目前最普遍的控制方法#实际运行的相关
事例和理论分析数据均表明#将这种控制规律用于大多数工业 对象会有较理想的结果'$( $ M#!控制在工业的运用最为广泛$
作为最早兴起的发展战略#这种控制战略不需要预备太多的专
电子信息 !"#!$%&$'(') *+&,-./&$01$21(3$&)%$4$$%<$
模糊控制MALTAB系统仿真实验报告

模糊控制MALTAB系统仿真实验报告可编程控制器智能控制技术仿真实验题目: 模糊控制系统MATLAB仿真实验报告院系名称:电气工程学院专业班级:电气学生姓名:学号:模糊控制系统MATLAB仿真实验报告一、实验目的 1、通过本次设计,了解模糊控制的基本原理、模糊模型的建立和模糊控制系统的设计过程。
2、熟悉在MATLAB下建立模糊控制器的方法,并能利用MATLAB对给定参数的模糊控制系统予以仿真二、实验项目1、实验题目本设计要求设计一个采用模糊控制的加热炉温度控制系统。
被控对象为一热处理工艺过程中的加热炉,加热设备为三相交流调压供电装置,输入控制信号电压为0~5V,输出相电压0~220V,输出最大功率180KW,炉温变化室温~625℃,电加热装置如图所示:图1-1电加热装置示意图3、实验数据:本实验输入变量为偏差e和偏差的变化ec,输出变量为控制电压U,变量模糊集量化论域均为[-6 6]采用的常用的三角形隶属函数。
控制规则表: U 输入变量ec NB NM NS ZO PS PM PB 输入变量 e NB NB NB NB NB NM NS ZO NM NB NB M, M, MS ZO ZO NS NV NM NM NS ZO ZO PS ZO NM NS NS ZO PS PS PM PS NS ZO ZO PS PM PM PB PM ZO ZO PS PM PM PB PB PB ZO PS PM PB PB PB PB 三、实验步骤 1、建立系统仿真图:在MATLAB主窗口单机工具栏中的Simulink快捷图标弹出“Simulink Library Browser”窗口,单击“Create a new model”快捷图标弹出模型编辑窗口。
依次将Signal Generator(信号源)、Subtract(减运算)、Gain(增益)、Derivative(微分)、Mux(合成)、Fuzzy Logic Controller(模糊逻辑控制器)、TransferFcn(传递函数)、Saturation(限幅)、Memory(存储器)、Scope(显示器)模块拖入窗口并连接成系统仿真图如图1-2 图1-2 系统仿真图 2、在模糊推理系统编辑器中设置变量:在MATLAB 命令窗口输入fuzzy并按回车键,启动FISEditor(模糊推理系统编辑器)。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
纸浆浓度调节系统的模糊控制及MATLAB仿真一、设计原理模糊控制器(Fuzzy Controller, FC)也称为模糊逻辑控制(Fuzzy Logic Controller, FLC),山于所采用的模糊控制规则是山模糊理论中的模糊条件语句描述的,因此模糊控制器是一种语言型控制器,故也称为模糊语言控制器(Fuzzy Language Controller, FLC)。
模糊控制是指基于模糊逻辑描述一个过程的控制算法,是以模糊集合论、模糊语言变量及模糊逻辑推理为基础的,基于被控系统的物理特性,模拟人的思维方式和人的控制经验来实现的一种计算机智能控制。
模糊控制器主要嵌有操作人员的经验和直觉知识,是模糊语言形式的控制方法,不需要预先知道被控对象结构、参数,不需要建立被控对象的精确数学模型,并能克服非线性因素、大惯性因素的影响,对调节对象的参数变化不敬感,对对象时变及纯滞后有一定的适应性,即具有较强的鲁棒性。
模糊控制器的设计•参数容易选择调整。
模糊控制系统的框图如图1所示:图1模糊控制系统框图在本设讣中,山于纸浆浓度调节系统中的电动执行器属于惯性环节错误!未指定书签。
,被控对象也属于惯性和纯滞后环节,所以釆用数字PID调节必产生严重的滞后效应,很难使系统取得良好的控制效果。
山上述可知,使用模糊控制器进行控制能得到较好的控制效果。
模糊控制器的设计大体可以概括为以下五个步骤:第一步:选定模糊控制器的输入输出变量第二步:根据输入输出变量确定模糊控制器的结构第三步:将输入变量的精确值变为模糊量,即模糊化处理第四步:确定控制规则第五步:有上述得到的控制模糊量计算精确的控制量,即解模糊化处理1、选定模糊控制器的输入输出变量,并进行量程转换输入语言变量选为实际浓度与给定值之间的偏差(纸浆浓度偏差)e及纸浆浓度偏差变化率ec,输出语言变量选为阀门开度增量u。
首先确定e、ec和u 的基本论域分别为彩〜%]、陟〜勾和[-12〜12],选定e、u的模糊集合的论域为卜6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6], ec 的模糊集合的论域为卜7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7]2、确定模糊控制器的结构根据系统输入变量个数可知,应采用釆用双输入单输出模糊控制器。
(如图2所示)模糊控制器主要包含三个功能环节:用于输入信号处理的模糊量化和模糊化环节,模糊控制算法功能单元,以及用于输出解模糊化的模糊判决环节。
图2双输入单输出模糊控制器3、确定各变量的模糊语言取值及相应的隶属函数,即进行模糊化模糊化是将模糊控制器输入量的确定值转换为相应模糊语言变量值的过程,此相应语言变量均由对应的隶属度函数来定义。
对纸浆浓度偏差e、纸浆浓度偏差变化率ec、阀门开度的增量u进行模糊化,分别用模糊语言变量X、Y、Z进行表示,语言值集合均为{负大,负中,负小,零,正小,正中,正大},用英文缩写进行表示分别为:X={NBe, NMe, NSe, ZOe, PSe, PMe, PBe}Y={ NBec, NMec, NSec, ZOec, PSec, PMec, PBec }Z= { NBu, NMu, NSu, ZOu, PSu, PMu, PBu }模糊化包括两个任务:笫一个任务是进行论域变换,过程参数的实际范圉称为基本论域,可以通过变换系数(量化因子)实现山基本论域到量化论域的变换; 第二个任务是求得输入对应于语言变量的隶属度。
取三角形隶属函数,并取为均非均匀间隔。
a.任务一:求量化因子e、ec和u的基本论域分别为低〜%]、[%〜%]和[-12〜12],量化论域分别为[-6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6], [-6, -5, -4, -3, -2,-1, 0, 1, 2, 3, 4, 5, 6], [-7, -6, -5, -4, -3, -2, -1, 0, 1, 2, 3, 4, 5, 6, 7]。
纸浆浓度偏差e的量化因子Ke=6/=500,纸浆浓度偏差变化率ec的量化因子Kec=6/=1000,通过量化因子即可实现由基本论域到量化论域的变换。
b.任务二:取隶属度函数选用三角形隶属度函数,如图3-5所示:input variable *1nput1"图3纸浆浓度偏差e的隶属度函数input variable ,,input2n图4纸浆浓度偏差变化率ec的隶属度函数output variable "outputl"图5阀门开度增量u的隶属度函数这样对于纸浆浓度偏差e、纸浆浓度偏差变化率e的不同输入值,可以根据对应的隶属度函数,把它模糊化成不同的语言值,这样就完成了模糊化。
4、建立模糊控制规则或控制算法根据人的直觉思维推理,山系统输出的误差和误差变化趋势来消除系统的误差的模糊控制规则,对于不同的被控对象,误差E,误差变化率EC及控制量U 有不同的意义。
在本设计中分别为纸浆浓度偏差e、纸浆浓度偏差变化率ec、阀门开度的增量u。
建立模糊控制规则是指规则的归纳和规则库的建立,是从实际控制经验过渡到模糊控制器的中心环节。
控制律通常山一组if-then结构的模糊条件语句构成, 或总结为模糊控制规则表。
例如:If (input 1 is NBe) and (input2 is NBec) then (output 1 is PBu) (1)即是模糊条件语句模糊控制表见任务书5、确定模糊推理和解模糊化方法输出的解模糊化就是将语言表达的模糊量恢复到精确的数值,也就是根据输出模糊子集的隶属度计算出确定数值。
二、设计过程及步骤1、模糊控制器的设计a.对系统的输入和输出进行设定对输入和输出的个数,词集个数和名称,量化论域进行设定。
具体步骤如下:打开matable窗口,在命令窗口中输入fuzzy,然后按下回车,将模糊控制器设置窗口打开,一般窗口中默认设置是单输入单输出,且有三个词集,在本设计中为双输入单输出系统,所以,首先添加一个输入(单击Edit—Add Variable---input),双击input 1,进入input 1 的编辑窗口,首先添加词集(单击Edit-Add MFs下拉菜单选4即可添加四个词集),根据要求更改各词集的名称和对应范围。
Input2与output 1的设定方法类似。
设定完毕后保存到workspace.如下图所示。
b •控制规则的设置双击上图中zfm出现控制规则编辑窗口,根据设讣任务书上所给的控制规则与模糊控制表编写控制规则,并在matable命令窗口中导出控制规则,如下所示:» a=readfis(zfm v);» showrule(a)ans =1.If (input 1 is NBe) and (input2 is NBec) then (output 1 is PBu) (1)2.If (input 1 is NMe) and (input2 is NBec) then (output 1 is PBu) (1)3.If (input 1 is NSe) and (input2 is NBec) then (output 1 is PMu) (1)4.If (input 1 is ZOe) and (input2 is NBec) then (output 1 is PMu) (1)5.If (input 1 is PSe) and (input2 is NBec) then (output 1 is PSu) (1)6.If (input 1 is PMe) and (input2 is NBec) then (output 1 is ZOu) (1)7.If (input 1 is PBe) and (input2 is NBec) then (output 1 is ZOu) (1)8.If (input 1 is NBe) and (input2 is NMec) then (output 1 is PBu) (1)9.If (input 1 is NMe) and (input2 is NMec) then (output 1 is PBu) (1)10.If (input 1 is NSe) and (input2 is NMec) then (output 1 is PMu) (1)11.If (input 1 is ZOe) and (input2 is NMec) then (output 1 is PMu) (1)12.If (input 1 is PSe) and (input2 is NMec) then (output 1 is PSu) (1)13.If (input 1 is PMe) and (input2 is NMec) then (output 1 is ZOu) (1)14.If (input 1 is PBe) and (input2 is NMec) then (output 1 is ZOu) (1)15.If (input 1 is NBe) and (input2 is NSec) then (output 1 is PBu) (1)16.If (input 1 is NMe) and (input2 is NSec) then (output 1 is PBu) (1)17.If (input 1 is NSe) and (input2 is NSec) then (output 1 is PMu) (1)18.If (input 1 is ZOe) and (input2 is NSec) then (output 1 is PSu) (1)19.If (input 1 is PSe) and (input2 is NSec) then (output 1 is ZOu) (1)20.If (input 1 is PMe) and (input2 is NSec) then (output 1 is NMu) (1)21.If (input 1 is PBe) and (input2 is NSec) then (output 1 is NMu) (1)22.If (input 1 is NBe) and (input2 is ZOec) then (output 1 is PBu) (1)23.If (input 1 is NMe) and (input2 is ZOec) then (output 1 is PBu) (1)24.If (input 1 is NSe) and (input2 is ZOec) then (output 1 is PMu) (1)25.If (input 1 is ZOe) and (input2 is ZOec) then (output 1 is ZOu) (1)26.If (input 1 is PSe) and (input2 is ZOec) then (output 1 is NMu) (1)27.If (input 1 is PMe) and (input2 is ZOec) then (output 1 is NBu) (1) 2& If (input 1 is PBe) and (input2 is ZOec) then (output 1 is NBu) (1)29.If (input 1 is NBe) and (input2 is PSec) then (output 1 is PMu) (1)30.If (input 1 is NMe) and (input2 is PSec) then (output 1 is PMu) (1)31.If (input 1 is NSe) and (input2 is PSec) then (output 1 is ZOu) (1)32.If (input 1 is ZOe) and (input2 is PSec) then (output 1 is NSu) (1)33.If (input 1 is PSe) and (input2 is PSec) then (output 1 is NMu) (1)34.If (input 1 is PMe) and (input2 is PSec) then (output 1 is NBu) (1)35.If (input 1 is PBe) and (input2 is PSec) then (output 1 is NBu) (1)36.If (input 1 is NBe) and (input2 is PMec) then (output 1 is ZOu) (1)37.If (input 1 is NMe) and (input2 is PMec) then (output 1 is ZOu) (1) 3& If (input 1 is NSe) and (input2 is PMec) then (output 1 is NSu) (1)39.If (input 1 is ZOe) and (input2 is PMec) then (output 1 is NMu) (1)40.If (input 1 is PSe) and (input2 is PMec) then (output 1 is NMu) (1)41.If (input 1 is PMe) and (input2 is PMec) then (output 1 is NBu) (1)42.If (input 1 is PBe) and (input2 is PMec) then (output 1 is NBu) (1)43.If (input 1 is NBe) and (input2 is PBec) then (output 1 is ZOu) (1)44.If (input 1 is NMe) and (input2 is PBec) then (output 1 is ZOu) (1)45.If (input 1 is NSe) and (input2 is PBec) then (output 1 is NSu) (1)46.If (input 1 is ZOe) and (input2 is PBec) then (output 1 is NMu) (1)47.If (input 1 is PSe) and (input2 is PBec) then (output 1 is NMu) (1)48.If (input 1 is PMe) and (input2 is PBec) then (output 1 is NBu) (1)49.If (input 1 is PBe) and (input2 is PBec) then (output 1 is NBu) (1) 保存到workspace,这样就完成了模糊控制器的设计。
